代码随想录算法训练营第47天 || 198.打家劫舍 || 213.打家劫舍II || 337.打家劫舍III
代码随想录算法训练营第47天 || 198.打家劫舍 || 213.打家劫舍II || 337.打家劫舍III
198.打家劫舍
题目介绍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
个人思路
动规五部曲
-
确定dp数组及其下标含义
dp[j]:从下标0到下标j的房间中,能偷的最大金额
-
确定递推公式
dp[i] = Integer.max(dp[i - 1], dp[i - 2] + nums[i]);表示偷或不偷当前房间对应的金额,其中取较大的那个;
-
初始化dp数组
dp[0] = nums[0]; dp[1] = Integer.max(dp[0], nums[1]);适应递推公式,从而初始化前两个dp数组元素
-
确定遍历顺序
正序遍历即可(结合递推公式)
-
打印dp数组检验
代码:
class Solution {public int rob(int[] nums) {if (nums.length == 1)return nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];dp[1] = Integer.max(dp[0], nums[1]);for (int i = 2; i < nums.length; i++) {dp[i] = Integer.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[dp.length - 1];}
}
213.打家劫舍II
题目介绍
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
思路解析
这道题看似只加了一个循环条件,但确实比较难考虑了不少。我一开始就想通过做标记的办法,决定最后加不加最后一个元素,过程中还得判断加与不加相等的情况(并且尽量取能加最后一个元素的情况)。但是发现会出现一种情况,最后一个元素大于第一个元素,但根据前面的取法,最后一位已经取不到了,导致答案错误。然后我就想能不能一开始比较始末位置的值,决定从大的一边去遍历,但这样要写两套相似的逻辑代码(当然可以函数封装,遍历+1/-1用一个变量存储即可),不过还是较为麻烦
题解解析
这个问题大致可以分为三种情况
- 去掉头尾的非环问题
- 去掉头的非环问题
- 去掉尾的非环问题
实际上情况2、3已经包括1了,因为dp[j]:表示的就是从头到j下标的最大偷盗价值,如果边界取不到,那就刚好等同于情况一。所以本题,我们只需要考虑后两种情况,然后取最大值即可(封装函数,调用两次,比较两个结果)
动规五部曲
-
确定dp数组及其下标含义
dp[j]:前j+1家能偷到的最大价值
-
确定递推公式
dp[i] = Integer.max(dp[i - 1], dp[i - 2] + nums[i+left]);还是与之前一样,偷与不偷当前房子的比较
-
初始化dp数组
dp[0] = nums[left]; dp[1] = Integer.max(dp[0], nums[left+1]); -
确定遍历顺序
正序遍历即可
-
打印dp数组检验
代码:
class Solution {public int rob(int[] nums) {if (nums.length == 1)return nums[0];int rob_max1 = rob_(nums, 1, nums.length - 1);int rob_max2 = rob_(nums, 0, nums.length - 2);return Integer.max(rob_max1,rob_max2);}public int rob_(int[] nums,int left,int right){if (right - left == 0)return nums[left];int[] dp = new int[right-left+1];dp[0] = nums[left];dp[1] = Integer.max(dp[0], nums[left+1]);for (int i = 2; i < dp.length; i++) {dp[i] = Integer.max(dp[i - 1], dp[i - 2] + nums[i+left]);}return dp[dp.length - 1];}
}
337.打家劫舍III
题目介绍
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AM0FWPIY-1677057886054)(null)]
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ubZdCCUF-1677057886010)(null)]
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
思路解析
结合动态规划和二叉树遍历的知识,每个结点都有偷和不被偷两种情况,那么我们分别记录每个节点的这两种情况的最优解,由下往上返回最优解,从子树最优得到全局最优(有点小贪心吧)
动规五部曲、递归三部曲
-
确定参数及返回值
参数:结点
返回值:int[2],偷与不偷当前结点的最大金额
-
确定终止条件
if (root == null)return new int[]{0, 0}; -
确定递归顺序
后序遍历
-
确定单层递归逻辑
-
确定dp数组及其下标含义
dp[0]:表示已当前结点为根的二叉树中,偷当前结点的最大金额
dp[1]:表示已当前结点为根的二叉树中,不偷当前结点的最大金额
-
确定递推公式
dp[0] = root.val + dp_left[1] + dp_right[1];//偷自己的情况下,子树只能取不偷的情况 //不偷自己的情况下,取偷或不偷左右孩子的最大值 dp[1] = Integer.max(dp_left[0], dp_left[1]) + Integer.max(dp_right[0], dp_right[1]);
-
-
最后取偷或不偷根节点的最大金额即可
class Solution {public int rob(TreeNode root) {int[] dp = traversal(root);return Integer.max(dp[0], dp[1]);}public int[] traversal(TreeNode root) {if (root == null)return new int[]{0, 0};int[] dp_left = traversal(root.left);int[] dp_right = traversal(root.right);int[] dp = new int[2];//0表示偷自己,1表示不偷自己dp[0] = root.val + dp_left[1] + dp_right[1];//不偷自己的情况下,取偷或不偷左右孩子的最大值dp[1] = Integer.max(dp_left[0], dp_left[1]) + Integer.max(dp_right[0], dp_right[1]);return dp;}
}
t.right);
int[] dp = new int[2];//0表示偷自己,1表示不偷自己
dp[0] = root.val + dp_left[1] + dp_right[1];
//不偷自己的情况下,取偷或不偷左右孩子的最大值
dp[1] = Integer.max(dp_left[0], dp_left[1]) + Integer.max(dp_right[0], dp_right[1]);
return dp;
}
}
相关文章:

代码随想录算法训练营第47天 || 198.打家劫舍 || 213.打家劫舍II || 337.打家劫舍III
代码随想录算法训练营第47天 || 198.打家劫舍 || 213.打家劫舍II || 337.打家劫舍III 198.打家劫舍 题目介绍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统&…...

JVM调优方式
对JVM内存的系统级的调优主要的目的是减少GC的频率和Full GC的次数。 1.Full GC 会对整个堆进行整理,包括Young、Tenured和Perm。Full GC因为需要对整个堆进行回收,所以比较慢,因此应该尽可能减少Full GC的次数。 2.导致Full GC的原因 1)年老…...

机器学习模型监控的 9 个技巧
机器学习 (ML) 模型是非常敏感的软件;它们的成功使用需要进行仔细监控以确保它们可以正常工作。当使用所述模型的输出自动做出业务决策时尤其如此。这意味着有缺陷的模型通常会对终端客户的体验产生真正的影响。因此,监控输入数据(和输出&…...

Linux 实现鼠标侧边键实现代码与网页的前进、后退
前言 之前一直是使用windows进行开发,最近转到linux后使用VsCode编写代码。 但是不像在win环境下,使用鼠标侧边键可以实现代码的前向、后向跳转。浏览网页时也不行(使用Alt Left可以后退)。 修改键盘映射实在没有那么方便&…...

健身蓝牙耳机推荐,推荐五款适合健身的蓝牙耳机
出门运动健身,有音乐的陪伴是我们坚持运动的不懈动力,在健身当中佩戴的耳机,佩戴舒适度以及牢固程度是我们十分需要注意的,还不知道如何选择健身蓝牙耳机,可以看看下面这些运动蓝牙耳机分享。 1、南卡Runner Pro4骨传…...
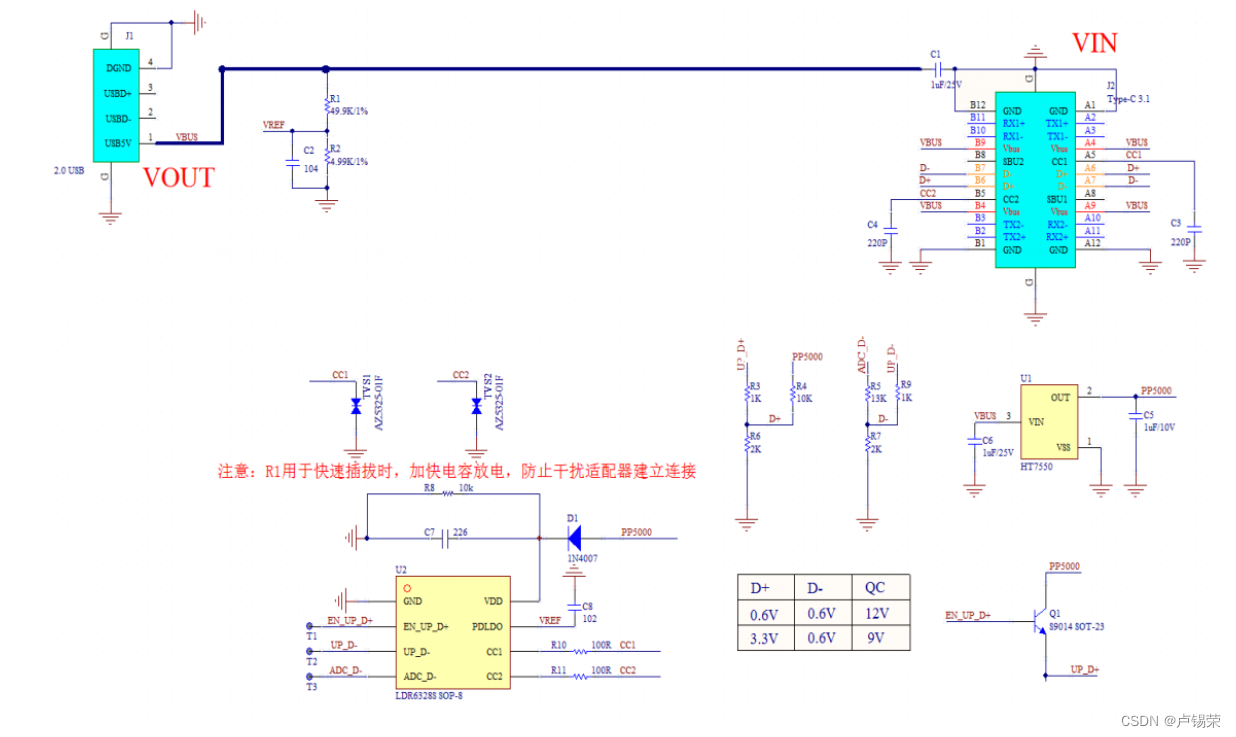
Type-c诱骗取电芯片大全
随着Type-C的普及和推广,目前市面上的电子设备正在慢慢淘汰micro-USB接口,逐渐都更新成了Type-C接口,micro-USB接口从2007年上市,已经陪伴我们走过十多个年头,如今也慢慢退出舞台。 今天我们评测的产品是市面上Type-C…...
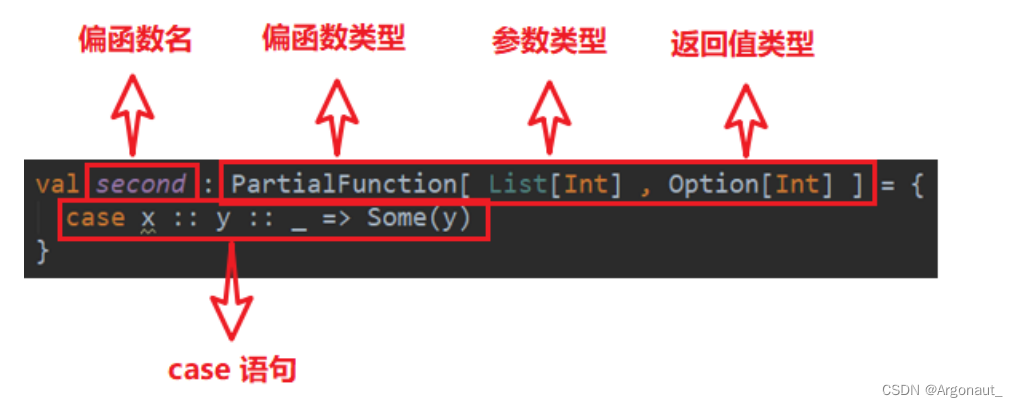
Scala模式匹配详解(第八章:基本语法、模式守卫、模式匹配类型)(尚硅谷笔记)
模式匹配第 8 章 模式匹配8.1 基本语法8.2 模式守卫8.3 模式匹配类型8.3.1 匹配常量8.3.2 匹配类型8.3.3 匹配数组8.3.4 匹配列表8.3.5 匹配元组8.3.6 匹配对象及样例类8.4 变量声明中的模式匹配8.5 for 表达式中的模式匹配8.6 偏函数中的模式匹配(了解)第 8 章 模式匹配 Scal…...
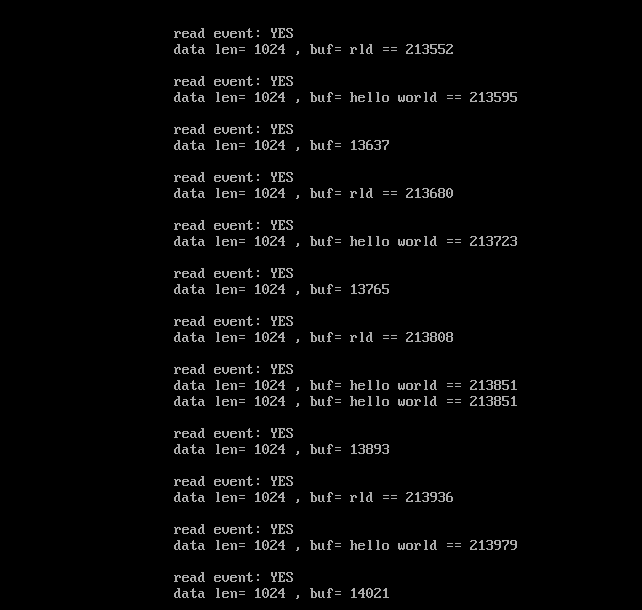
Linux:基于libevent读写管道代码
基于libevent读写管道代码: 读端: #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <string.h> #include <event2/event.h> #include…...

2022年中职网络安全逆向题目整理合集
中职网络安全逆向题目整理合集逆向分析:PE01.exe算法破解:flag0072算法破解:flag0073算法破解:CrackMe.exe远程代码执行渗透测试天津逆向re1 re2逆向分析:PE01.exe FTPServer20220509(关闭链接) FTP用户名:PE01密码…...
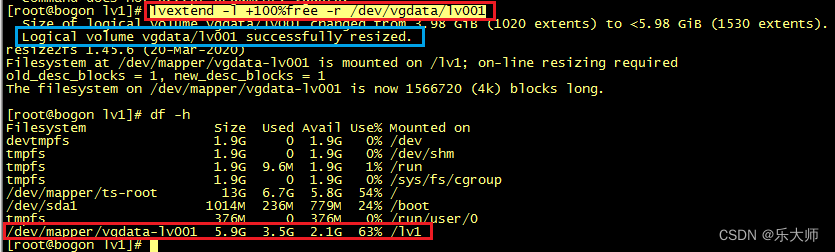
Tencent OS下逻辑卷(LVM)增加硬盘扩容
上一篇文章写了逻辑卷创建以及使用剩余空间为已经创建的逻辑卷扩容。 本篇是针对卷组空间已经用尽时的扩容方法。那就是增加硬盘。 首先我们为虚拟机增加硬盘/dev/sdd 使用fdisk为/dev/sdd分区,方法在上一篇文章已经描述,在此不再赘述。 新增的硬盘使用如下命令添加到卷组…...
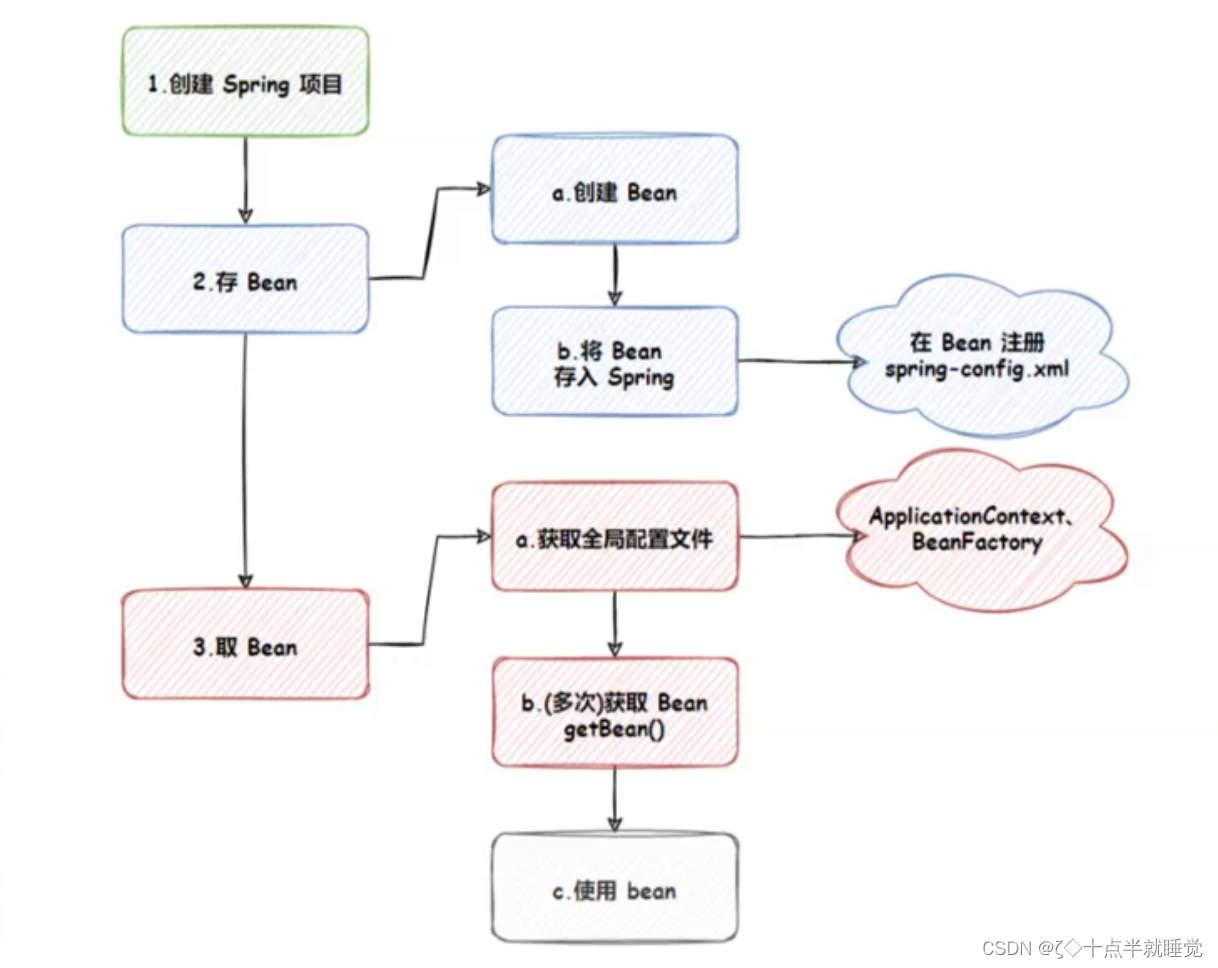
【Java】Spring的创建和使用
Spring的创建和使用 Spring就是一个包含众多工具方法的IOC容器。既然是容器,那么就具备两个最主要的功能: 将对象存储到容器中从容器中将对象取出来 在Java语言当中对象也叫作Bean。 1. 创建Spring项目 创建一个普通maven项目添加Spring框架支持(spri…...
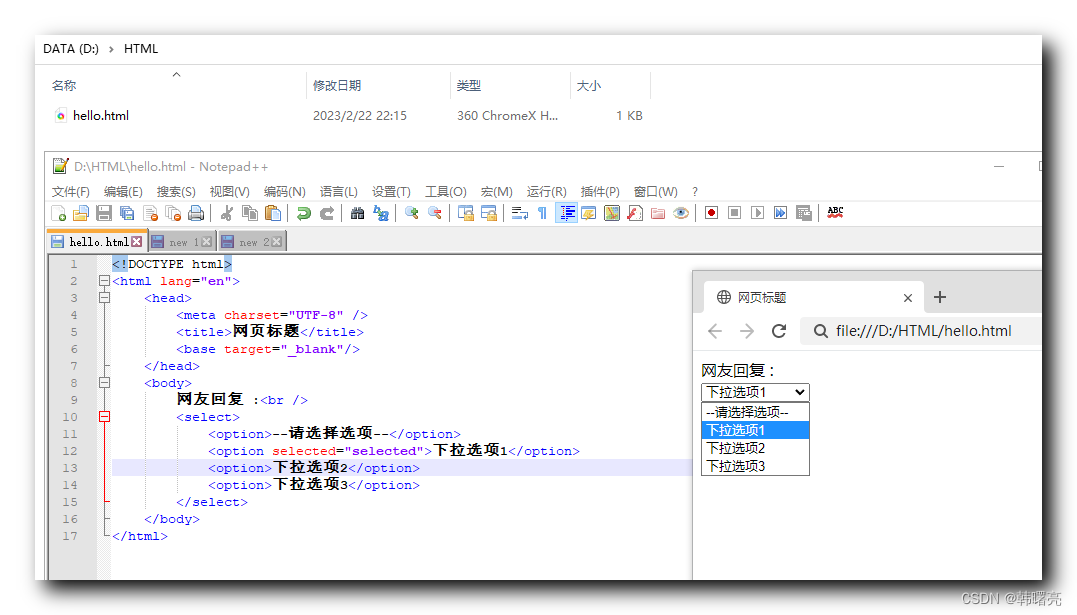
【HTML】HTML 表单 ④ ( textarea 文本域控件 | select 下拉列表控件 )
文章目录一、textarea 文本域控件二、select 下拉列表控件一、textarea 文本域控件 textarea 文本域 控件 是 多行文本输入框 , 标签语法格式如下 : <textarea cols"每行文字字符数" rows"文本行数">多行文本内容 </textarea>实际开发中 并不…...

MySQL 操作 JSON 数据类型
MySQL 从 v5.7.8 开始支持 JSON 数据类型。 JSON 数据类型和传统数据类型的操作还是有很大的差别,需要单独学习掌握。好在 JSON 数据类型的学习成本不算太高,只是在 SQL 语句中扩展了 JSON 函数,操作 JSON 数据类型主要是对函数的学习。 新…...

关于vue3生命周期的使用、了解以及用途(详细版)
生命周期目录前言组合式写法没有 beforeCreate / created 生命周期,并且组合式写生命周期用哪个先引哪个beforeCreatecreatedbeforeMount/onBeforeMountmounted/onMountedbeforeUpdate/onBeforeUpdateupdated/onUpdatedbeforeUnmount/onBeforeUnmountunmounted/onUn…...

2月,真的不要跳槽。
新年已经过去,马上就到金三银四跳槽季了,一些不满现状,被外界的“高薪”“好福利”吸引的人,一般就在这时候毅然决然地跳槽了。 在此展示一套学习笔记 / 面试手册,年后跳槽的朋友可以好好刷一刷,还是挺有必…...

Vulnhub靶场----4、DC-4
文章目录一、环境搭建二、渗透流程三、思路总结一、环境搭建 DC-4下载地址:https://download.vulnhub.com/dc/DC-4.zip kali:192.168.144.148 DC-4:192.168.144.152 二、渗透流程 端口扫描:nmap -T5 -p- -sV -sT -A 192.168.144.1…...
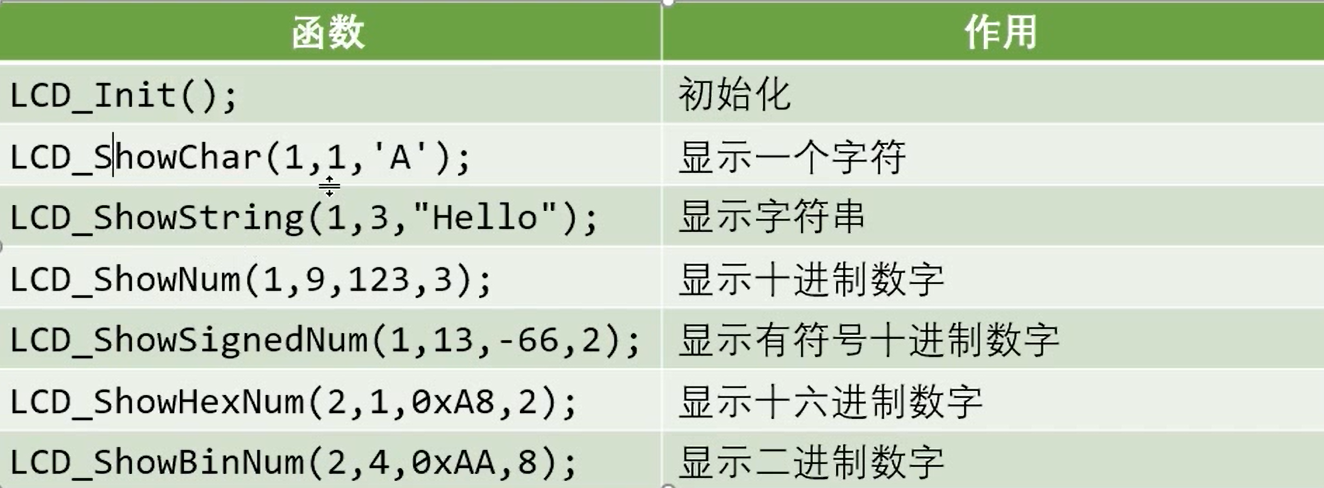
51单片机学习笔记_12 LCD1602 原理及其模块化代码
LCD1602 liquid crystal display 液晶显示屏,一种字符型液晶显示模块,可以显示 16*2 个字符,每个字符是 5*7 点阵。 P0 P2 会和数码管、LED 一定程度上冲突。 地。 Vcc。 调对比度的。 RS:数据指令端。1代表 DB 是数据&#x…...
科技 “新贵”ChatGPT 缘何 “昙花一现” ,仅低代码风靡至今
恍惚之间,ChatGPT红遍全网,元宇宙沉入深海…… 在科技圈,见证了太多“昙花一现”,“新贵” ChatGPT 的爆火几乎复制了元宇宙的路径,它会步元宇宙的后尘,成为下一个沉入深海的工具吗? 不可否认的…...

redis基本入门| 怎么安装redis?什么的是redis?怎么使用?
目录 一、Redis下载与安装 二、基本概念 1.什么是Redis? 2.Redis端口多少? 3.Redis是单线程还是多线程? 4.Redis为什么单线程还这么快? 三、Redis的基本操作 四、Redis的五个基本类型 1.Redis-key 2.字符串 string 3.列表 list …...
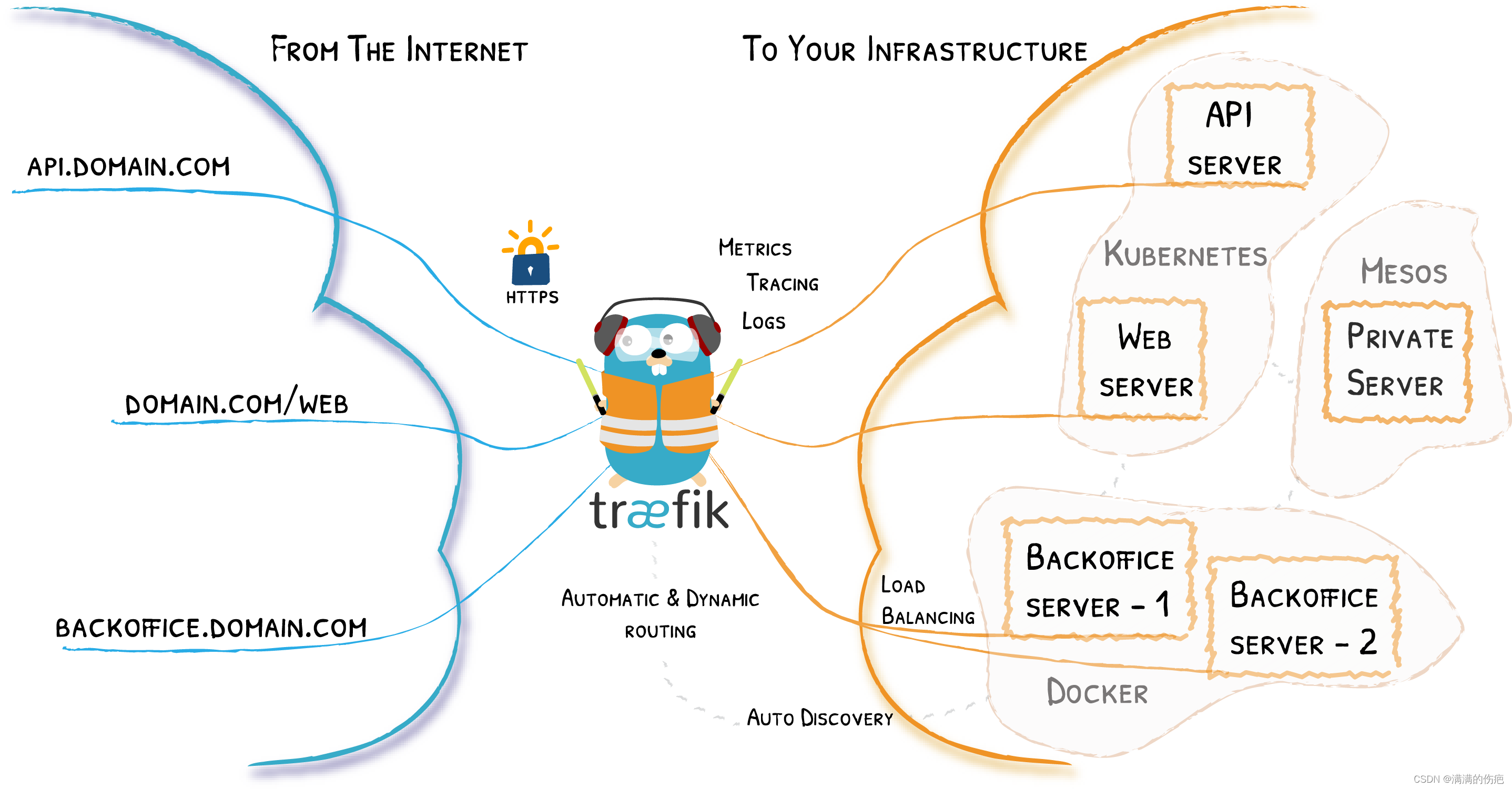
kubernetes traefik ingress 安装部署以及使用和注意点
1、简介 Traefik 是一款 open-source 边缘路由器,可让您轻松地发布服务. 它接收来自您的系统请求,并找出负责处理它们的后端服务组件。 traefik 与众不同在于它能够自动发现适合您服务的配置。 当 Traefik 检查您的基础设施时,它会发现相关信…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
