leetcode 42, 58, 14(*)
42. Trapping Rain Water
1.暴力解法(未通过)
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;for(int i=0; i<n; i++){int r_max = 0, l_max= 0;for(int j = i; j<n; j++)r_max = max(r_max, height[j]);for(int j=i; j>=0; j--)l_max = max(l_max, height[j]);res += min(r_max, l_max) - height[i];}return res;}
};解法的基本思路:
要把每一段拆分出来
某一竖条的储水量怎么求? 他的高度是左边最大 和 右边最大 取的最小值,然后再减去自身的高度
2.备忘录
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;vector<int> r_max(n, 0);vector<int> l_max(n, 0);l_max[0] = height[0];r_max[n-1] = height[n-1];for(int i=1; i<n; i++)l_max[i] = max(height[i], l_max[i-1]);for(int i=n-2; i>=0; i--)r_max[i] = max(height[i], r_max[i+1]);for(int i=0; i<n; i++){res += min(r_max[i], l_max[i]) - height[i];}return res;}
};这里就是把每一次的最大最小值都记录下来,就不用每次都遍历了,跟上一个思想没有区别
3.双指针法
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int l_max = 0, r_max = 0;int res = 0;int left = 0, right = n-1;while(left < right){l_max = max(l_max, height[left]);r_max = max(r_max, height[right]);if(l_max < r_max){res += l_max - height[left];left++;}else{res += r_max - height[right];right--;}}return res;}
};这里的l_max是【0, left】的最大值,r_max是【right, n-1】的最大值
为什么这样可以呢?因为其实只要一边找到最大值了,无论另一边是不是最大值,只要比它大,那么一定能兜住他
58. Length of Last Word
class Solution {
public:int lengthOfLastWord(string s) {int res = 0;int tail = s.size()-1;while(tail >= 0 && s[tail] == ' ') tail--;while(tail >=0 && s[tail] != ' '){res++;tail--;}return res;}
};因为最后也有可能有空格,所以从后面开始
14. Longest Common Prefix
class Solution {
public:string longestCommonPrefix(vector<string>& strs) {int n = strs.size();string res = "";sort(strs.begin(), strs.end());string a = strs[0];string b = strs[n-1];int i=0;while(i<a.size() && i<b.size()){if(a[i] != b[i]) break;res += a[i];i++;}return res;}
};这里用到sort, sort的最前和最后是最不相关的两个string
相关文章:
)
leetcode 42, 58, 14(*)
42. Trapping Rain Water 1.暴力解法(未通过) class Solution { public:int trap(vector<int>& height) {int n height.size();int res 0;for(int i0; i<n; i){int r_max 0, l_max 0;for(int j i; j<n; j)r_max max(r_max, heigh…...

SpringCloud-微服务CAP原则
接上文 SpringCloud-Config配置中心 到此部分即微服务的入门。 总的来说,数据存放的节点数越多,分区容忍性就越高,但要复制更新的次数就越多,一致性就越难保证。同时为了保证一致性,更新所有节点数据所需要的时间就…...
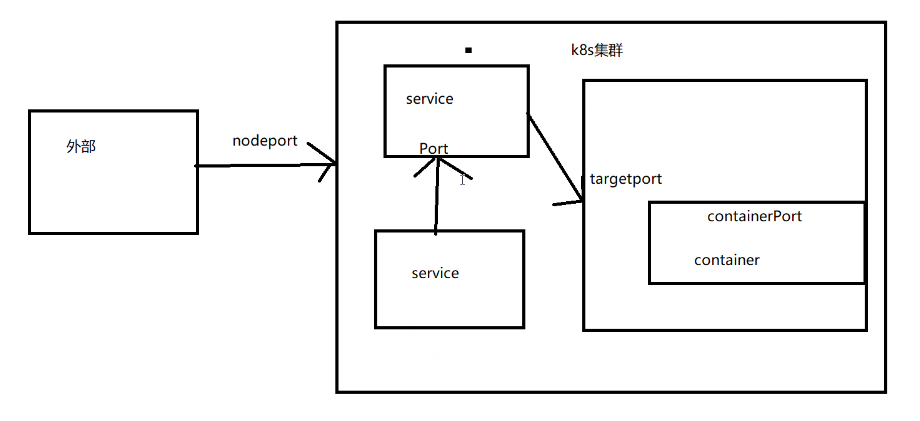
K8S:Yaml文件详解
目录 一.Yaml文件详解 1.Yaml文件格式 2.YAML 语法格式 二.Yaml文件编写及相关概念 1.查看 api 资源版本标签 2.yaml编写案例 (2)Deployment类型编写nginx服务 (3)k8s集群中的port介绍 (5)快速编写yaml文件 …...
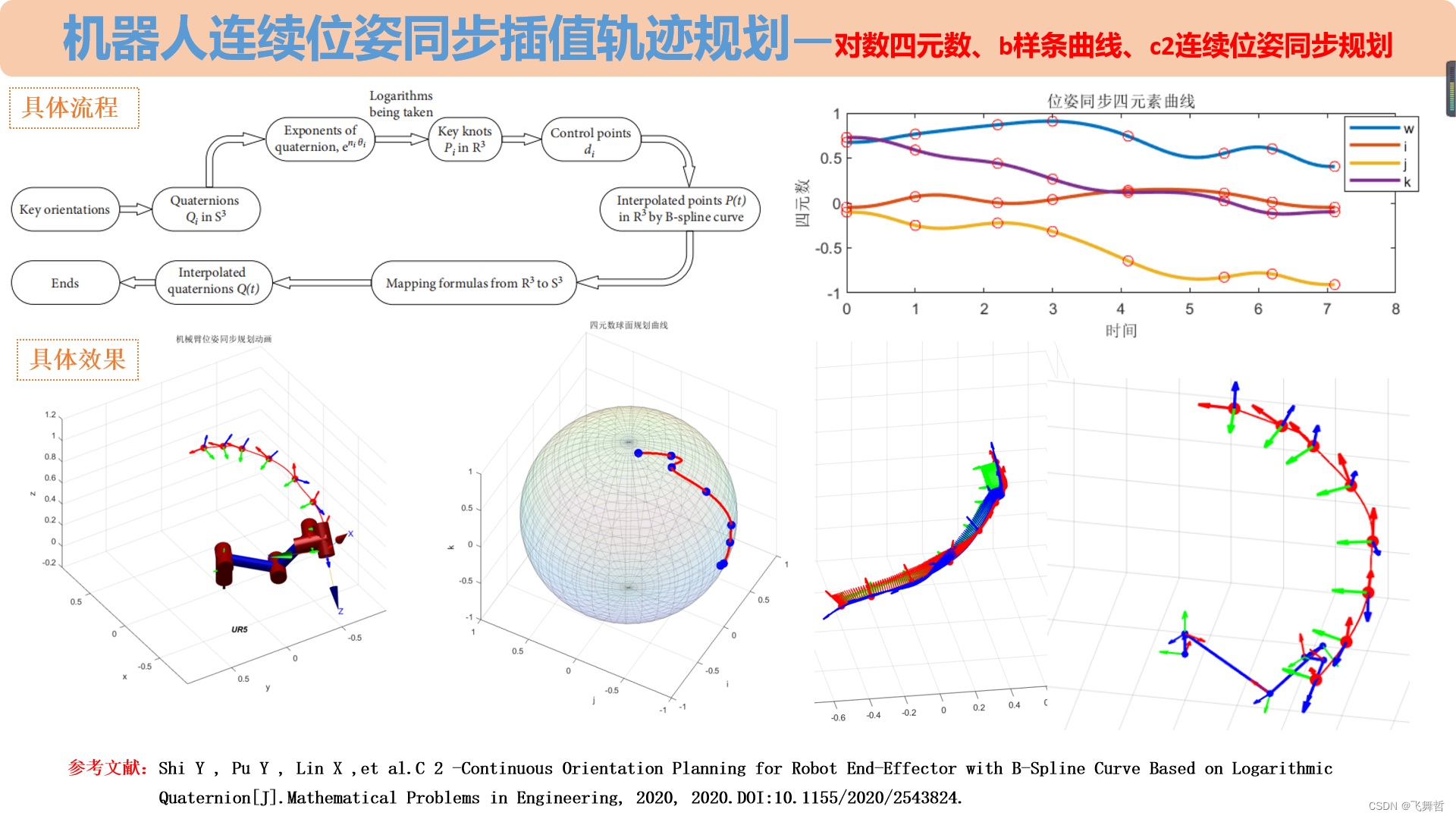
机器人连续位姿同步插值轨迹规划—对数四元数、b样条曲线、c2连续位姿同步规划
简介:Smooth orientation planning is benefificial for the working performance and service life of industrial robots, keeping robots from violent impacts and shocks caused by discontinuous orientation planning. Nevertheless, the popular used quate…...
三维模型3DTile格式轻量化压缩的遇到常见问题与处理方法分析
三维模型3DTile格式轻量化压缩的遇到常见问题与处理方法分析 三维模型的轻量化压缩是一项技术挑战,特别是在处理复杂的3DTile格式时。下面列举了一些处理过程中可能遇到的常见问题以及相应的处理方法: 模型精度损失:在进行压缩处理时&#x…...
2023-简单点-开启防火墙后,ping显示请求超时;windows共享盘挂在不上
情景描述 树莓派 挂载 windows共享盘 之前一直可以,突然有一天不行了 ping xxxx不通了 一查,或许是服务器被同事开了防火墙,默认关闭了ping的回显 操作: 开启ping回显cmd ping通了,但是挂载还是不行, 显示 dmesg命…...

华为Java工程师面试题
常见问题: 什么是Java虚拟机(JVM)?它与现实中的计算机有什么不同?Java中的基本数据类型有哪些?它们的范围是什么?什么是引用类型?Java中的引用类型有哪些?什么是对象&am…...

大数据Flink(七十四):SQL的滑动窗口(HOP)
文章目录 SQL的滑动窗口(HOP) SQL的滑动窗口(HOP) 滑动窗口定义:滑动窗口也是将元素指定给固定长度的窗口。与滚动窗口功能一样,也有窗口大小的概念。不一样的地方在于,滑动窗口有另一个参数控制窗口计算的频率(滑动窗口滑动的步长)。因此,如果滑动的步长小于窗口大…...
Hystrix和Sentinel熔断降级设计理念
目录 1 基本介绍2 Hystrix信号量和线程池区别2.1 信号量模式2.2 线程池模式2.3 注意 3 Sentinel介绍 1 基本介绍 Sentinel 和 Hystrix 的原则是一致的: 当检测到调用链路中某个资源出现不稳定的表现,例如请求响应时间长或异常比例升高的时候,则对这个资源…...
获取Windows 10中的照片(旧版)下载
Windows 10中的新版照片应用,目前发现无法直接打开部分iOS设备上存储的照片。需要使用照片(旧版)才行。 但目前应用商店中无法直接搜索到照片(旧版),因此笔者提供如下链接,可以直接访问并呼出W…...
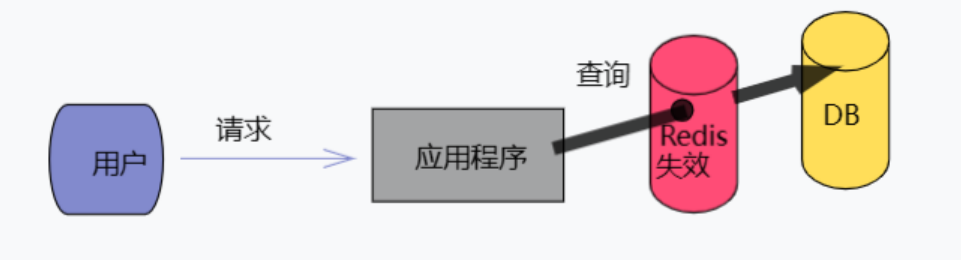
【Redis】Redis作为缓存
【Redis】Redis常见面试题(2) 文章目录 【Redis】Redis常见面试题(2)1. 缓存2. Redis作为缓存2.1 缓存雪崩2.2 缓存穿透2.3 缓存击穿2.4 缓存雪崩、缓存穿透、缓存击穿的区别2.5 缓存预热2.6 如何保证缓存和MySQL双写一致 【Redis…...

IDEA(2023)解决运行乱码问题
😇作者介绍:一个有梦想、有理想、有目标的,且渴望能够学有所成的追梦人。 🎆学习格言:不读书的人,思想就会停止。——狄德罗 ⛪️个人主页:进入博主主页 🗼专栏系列:无 🌼…...
零基础学前端(二)用简单案例去理解 HTML 、CSS 、JavaScript 概念
该篇适用于从零基础学习前端的小白 初学者不懂代码得含义也要坚持模仿逐行敲代码,以身体感悟带动头脑去理解新知识 一、导言 HTML,CSS,JavaScript 都是单独的语言;他们构成前端技术基础; (1)HTM…...
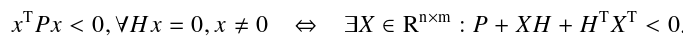
线性矩阵不等式(LMI)在控制理论中的应用
目录 (一)Matlab中的LMI处理工具包 (二)为什么LMI成为控制理论领域重要工具? (三)LMI在与Lyapunov不等式的关系 (1)线性矩阵不等式 (2)线性矩阵…...

如何在Python爬虫程序中使用HTTP代理?
在进行网络爬虫时,我们经常需要使用代理服务器来隐藏自己的真实IP地址,以避免被目标网站封禁或限制访问。本文将介绍如何将HTTP代理配置到Python爬虫程序中使用。 什么是HTTP代理? HTTP代理是一种网络代理,它充当客户端和服务器之…...

ARM架构指令集--专用指令
四、状态寄存器专用指令 CPSR寄存器-N Z C V T为0时 为ARM状态 F为0时 为开启FIQ状态 I为0时 为开启IRQ状态 图1 图2 一开始都是SVC指令,因为在操作系统启动的时候,在做一些初始化的操作,不允许被打断 图3 复位后CPSR寄存器为0xD3--…...

免费IP类api接口:含ip查询、ip应用场景查询、ip代理识别、IP行业查询...
免费IP类api接口:含ip查询、ip应用场景查询、ip代理识别… IP归属地-IPv6区县级:根据IP地址(IPv6版本)查询归属地信息,包含国家、省、市、区县和运营商等信息。IP归属地-IPv6城市级:根据IP地址(…...

Android Studio 中AGP ,Gradle ,JDK,SDK都是什么?
当进行 Android 开发时,以下是关键概念和工具的解释: Android Gradle Plugin: Android Gradle Plugin 是一个由 Google 提供的构建工具,它与 Gradle 配合使用来构建和打包 Android 应用。它提供了一组任务和功能,使开发…...
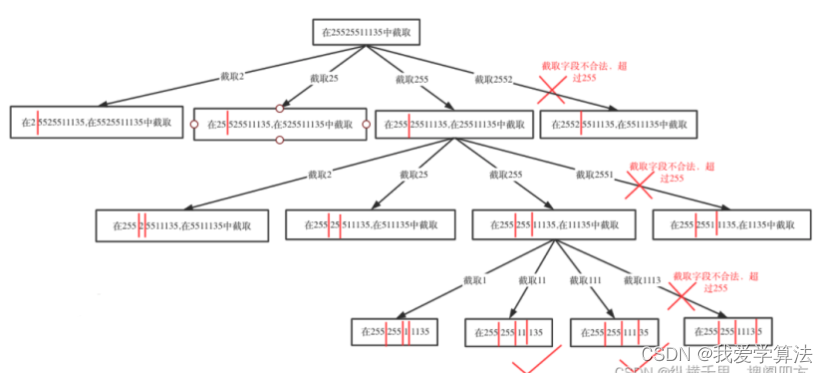
算法通关18关 | 回溯模板如何解决复原IP问题
18关的前几篇文章看过之后,对回溯的模板问题基本解题思路就知道了,就是固定的for循环问题,外层for循环控制横向,递归控制纵向,还要考虑撤销操作和元素是否能被重复利用问题,重复利用的情景较少,…...

Layui快速入门之第五节 导航
目录 一:基本概念 导航依赖element模块 API 渲染 属性 事件 二:水平导航 常规用法: 三:垂直导航 四:侧边垂直导航 五:导航主题 六:加入徽章等元素 七:面包屑导航 ps&a…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
