当前位置： 首页 > news >正文

由一个多线程并发保存而引发的思考

news 文章来源：https://blog.csdn.net/u014534808/article/details/132865781 2025/1/8 2:23:59

1. 问题描述

问题描述，现A表（用户查看实验的次数）有user_id和exp_id两个字段，其中user_id加exp_id不唯一。B表有user_id，exp_id以及exp_num三个字段，其中user_id加exp_id唯一（表中未建唯一索引）。

现需要将A表的数据同步到B表，单机模式通过定时任务同步。A表的数据有10万条，为了提高同步效率，采用多线程并发同步。主线程按照游标分页查询，每页查询500条，然后将每页的数据都给独立的线程执行。为了保证user_id加exp_id唯一，只能在程序中通过加锁控制。首先按照 userId+"_"+expId给这500条数据分组，然后循环分组，在循环中通过synchronized来加锁，锁的对象是userId+"_"+expId，它是一个字符串，userId+"_"+expId相同的则锁住，不同的则放过。

protected void batchMigrate(List<

相关文章：

由一个多线程并发保存而引发的思考

1. 问题描述 问题描述，现A表（用户查看实验的次数）有user_id和exp_id两个字段，其中user_id加exp_id不唯一。B表有user_id，exp_id以及exp_num三个字段，其中user_id加exp_id唯一（表中未建唯一索引）。 现需要将A表的数据同步到B表，单机模式通过定时任务同步。A表的数据有…...

编程日记 2023/9/14 9:21:44

python-vlc

文章目录 关于 python-vlc安装使用关于 python-vlc Python vlc bindings github : https://github.com/oaubert/python-vlcPython bindings (ctypes-based) for VLC http://olivieraubert.net/vlc/python-ctypes/关于 VLC 可参考 macOS - 安装使用 VLC https://blog.csdn.net/…...

编程日记 2023/9/14 9:20:43

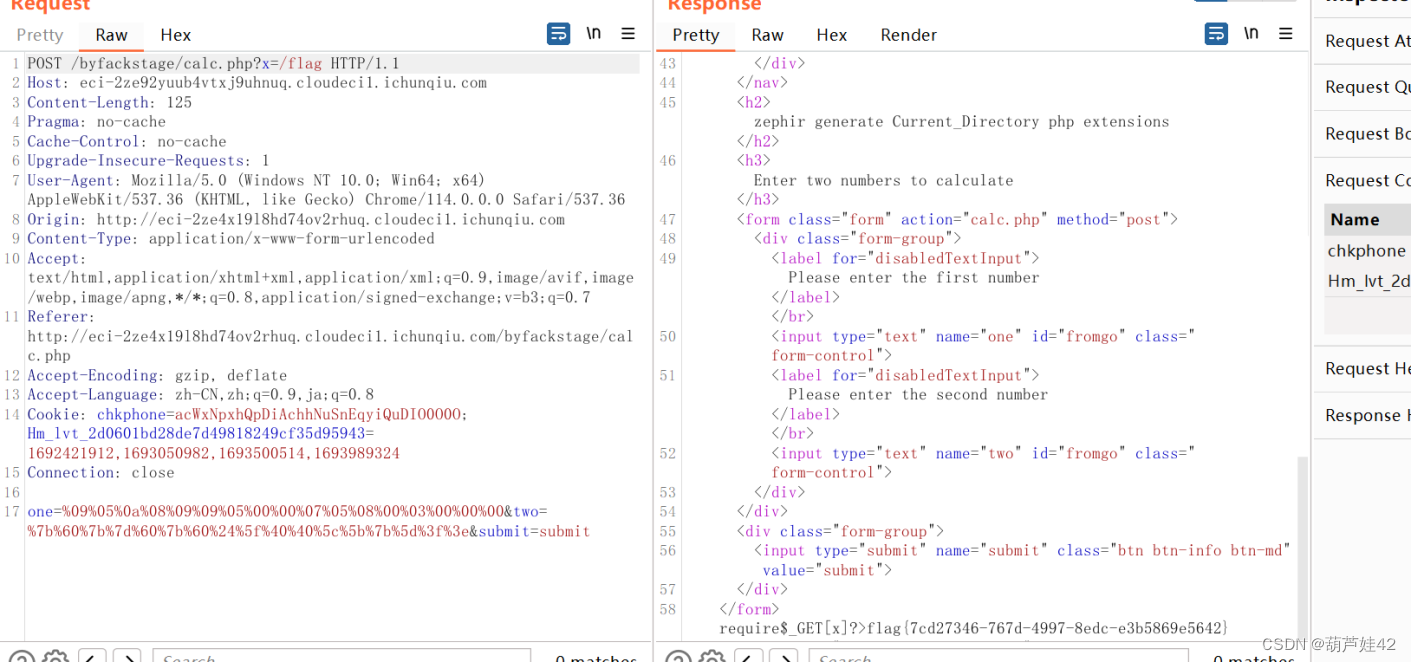
2023长城杯 web部分题目(seekingeasy_extension)

seeking 下载题目附件得到&#xff1a; <?php error_reporting(0); header("HINT:POST n range(1,10)");$image $_GET[image]; echo "这里什么也没有&#xff0c;或许吧。"; $allow range(1, 10); shuffle($allow); if (($_POST[n] $allow[0])) …...

编程日记 2023/9/14 9:19:42

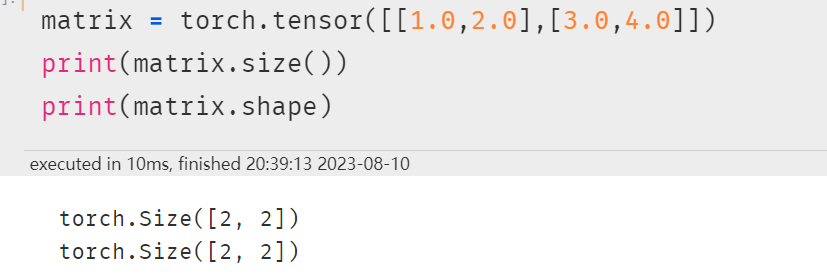
2-1 张量数据结构

张量概念 张量是什么&#xff1f; 单个元素叫标量&#xff08;scalar&#xff09;&#xff0c;一个序列叫向量&#xff08;vector&#xff09;&#xff0c;多个序列组成的平面叫矩阵&#xff08;matrix&#xff09;&#xff0c;多个平面组成的立方体叫张量&#xff08;tensor&…...

编程日记 2023/9/14 9:17:41

QSqlQuery查询语句

SqlQuery 封装了在 QSqlDatabase 上执行的 SQL 查询中创建、导航和检索数据所涉及的功能。 可用于执行 DML&#xff08;数据操作语言&#xff09;语句&#xff0c;如 SELECT、INSERT、UPDATE 和 DELETE&#xff0c; 以及 DDL&#xff08;数据定义语言&#xff09;语句&#xff…...

编程日记 2023/9/14 9:15:36

用c语言编写出三底模型

以下是一个用C语言实现三底模型的示例代码。这个程序通过循环遍历输入的股票数据&#xff0c;判断是否出现三底形态&#xff0c;如果是&#xff0c;则输出买入信号&#xff0c;否则输出卖出信号。 c语言 #include <stdio.h> #include <stdlib.h> // 判断是否出现…...

编程日记 2023/9/14 9:13:34

15 Python使用MySQL

概述 在上一节&#xff0c;我们介绍了如何在Python中使用网络&#xff0c;包括&#xff1a;套接字编程、socketserver等内容。在这一节&#xff0c;我们将介绍如何在Python中使用MySQL。MySQL是最流行的关系型数据库管理系统之一&#xff0c;由瑞典MySQL AB公司开发&#xff0c…...

编程日记 2023/9/14 9:12:34

3、Nginx 常用的命令和配置文件

文章目录 3、nginx 常用的命令和配置文件3.1 nginx 常用的命令&#xff1a;3.2 nginx.conf 配置文件3.2.1 地址3.2.2 内容3.2.2 vim不正常退出后再次打开信息提示解决方法 3.3 第一部分&#xff1a;全局块3.4 第二部分&#xff1a;events 块3.4 第三部分&#xff1a;http 块①、…...

编程日记 2023/9/14 9:05:27

python经典百题之兔子出生问题

这是一个经典的 Fibonacci 数列问题&#xff0c;可以通过递归或循环来解决。 递归方法&#xff1a; 由题意可知&#xff0c;第 n 个月的兔子数等于第 n-1 个月的兔子数加上第 n-2 个月的兔子数。设 f(n) 表示第 n 个月的兔子数&#xff0c;则有&#xff1a; f(n) f(n-1) f…...

编程日记 2023/9/14 9:03:25

不定积分的概念和性质

目录 原函数 不定积分 不定积分的几何意义 原函数的存在定理 不定积分的性质 不定积分是微积分的一个关键部分&#xff0c;它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数&#xff0c;也被称为反导数。原函数是一个函数&#xff0c;使得该函数的…...

编程日记 2023/9/14 9:02:25

远程访问服务器JupyterLab的配置方法

远程访问服务器JupyterLab的配置方法 环境及工具注意 基本步骤生成密码生成并修改配置文件*错误&#xff1a;jupyter localhost 已拒绝连接*后台运行jupyter后台关闭 其实就是在服务器运行JupyterLab&#xff0c;然后在本地浏览器访问 环境及工具 服务器&#xff1a;Ubuntu 1…...

编程日记 2023/9/14 8:58:22

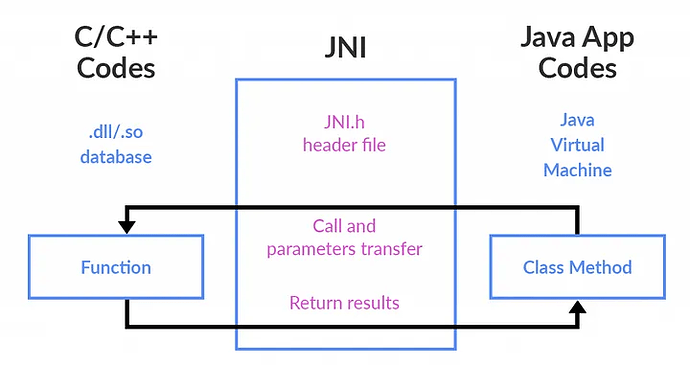
Java native 关键字

如你在看 JDK 的源代码的时候&#xff0c;大概率会看到很多方法使用了 native 关键字。 下面是 String 对象 JDK 中的源代码&#xff0c;就带有了一个 native 关键字。 native 是干什么用的 简单来说就是 Java 的 native 方法的实现不是用 Java 实现的&#xff0c;可能在其他…...

编程日记 2023/9/14 8:56:19

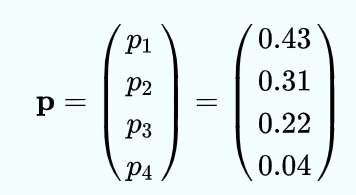
【线性代数】沉浸式线性代数在线学习网站

地址&#xff1a;http://immersivemath.com/ila/index.html 这是全球第一本带交互式图形的线性代数教材&#xff0c;作者是 J. Strm, K. strm, and T. Akenine-Mller。 全书一共十章&#xff0c;各章节内容如下&#xff1a; 接下来我将对各章节进行简单的总结&#xff0c;另外…...

编程日记 2023/9/14 8:55:19

Kotlin中特性、数据类、伴生对象、顶层函数

Kotlin中的函数参数和属性声明 在 Kotlin 中&#xff0c;函数参数和属性有不同的声明方式和行为。这些特性使得 Kotlin 代码更加安全、易于理解和维护。 函数参数的只读性 fun sum(a: Int, b: Int): Int {var modifiedA aif (modifiedA > 0) {modifiedA 1}//三元表达式v…...

编程日记 2023/9/14 8:53:17

《PostgreSQL物化视图：创建、维护与应用》

&#x1f337;&#x1f341; 博主猫头虎&#xff08;&#x1f405;&#x1f43e;&#xff09;带您 Go to New World✨&#x1f341; &#x1f405;&#x1f43e;猫头虎建议程序员必备技术栈一览表&#x1f4d6;&#xff1a; &#x1f6e0;️ 全栈技术 Full Stack: &#x1f4da…...

编程日记 2023/9/14 8:52:15

shell脚本之test命令

shell脚本之test命令 数值比较&#xff1a;2. 字符串比较&#xff1a;3. 文件测试&#xff1a;4. 逻辑操作&#xff1a;5. 其他测试&#xff1a; test命令在Shell脚本中用于进行条件测试和条件判断。它用于检查文件、字符串和数值的各种条件&#xff0c;并返回一个状态码&#…...

编程日记 2023/9/14 8:49:13

JAVA设计模式8：装饰模式，动态地将责任附加到对象上，扩展对象的功能

作者主页&#xff1a;Designer 小郑 作者简介&#xff1a;3年JAVA全栈开发经验&#xff0c;专注JAVA技术、系统定制、远程指导&#xff0c;致力于企业数字化转型&#xff0c;CSDN博客专家&#xff0c;阿里云社区专家博主&#xff0c;蓝桥云课讲师。 目录 一、什么是装饰模式二、…...

编程日记 2023/9/14 8:46:09

Linux学习之MySQL备份

xtrabackup资源下载 完全备份与恢复 # 1.物理备份与恢复 # 冷备份&#xff0c;需停止数据库服务 适合线下服务器。 [rootmysql50 ~]# systemctl stop mysqld [rootmysql50 ~]# mkdir /bakdir [rootmysql50 ~]# cp -r /var/lib/mysql /bakdir/mysql.bak [rootmysql50 ~]# cd /…...

编程日记 2023/9/14 8:44:08

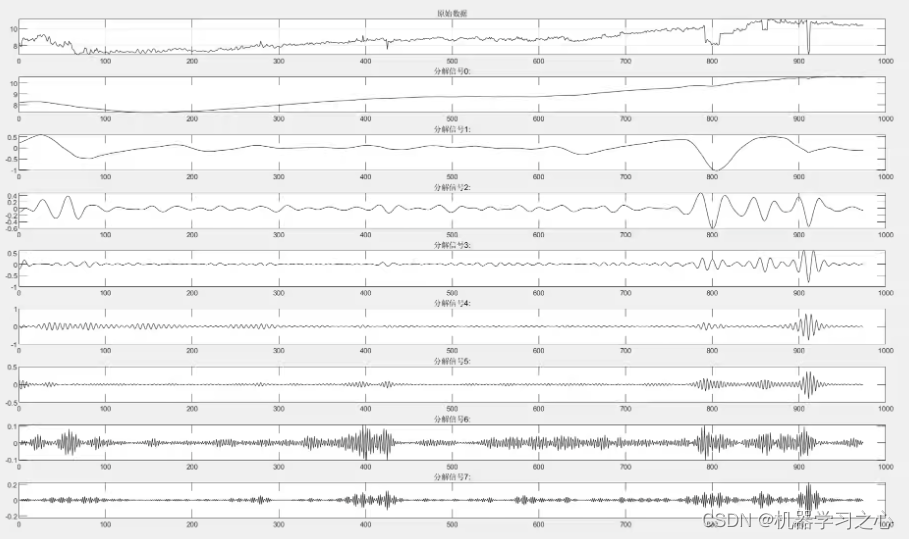
时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化

时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化 目录 时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 北方苍鹰优化算法NGO优化VMD&#xff0c;对其分解层数&#xff0c;惩罚因子数做优化…...

编程日记 2023/9/14 8:43:07

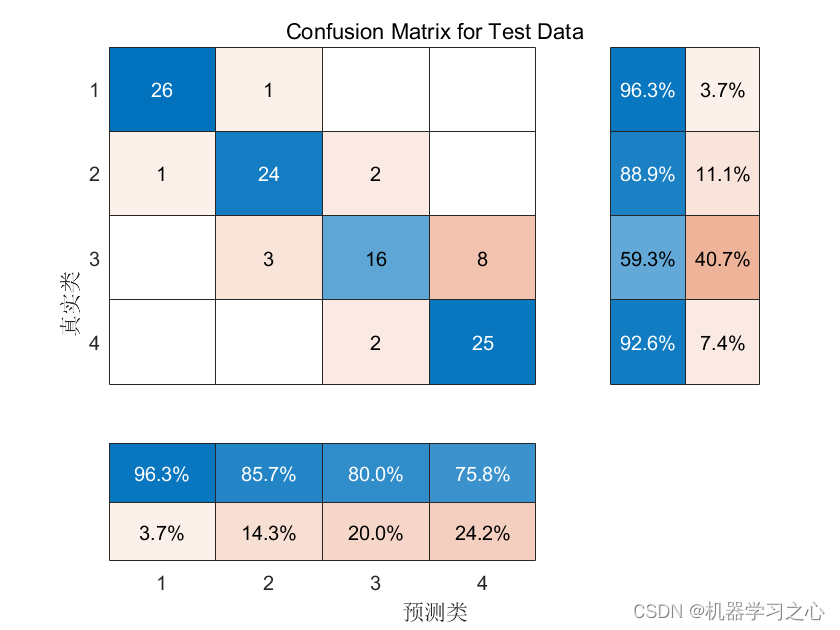
分类预测 | Matlab实现RBF-Adaboost多特征分类预测

分类预测 | Matlab实现RBF-Adaboost多特征分类预测 目录 分类预测 | Matlab实现RBF-Adaboost多特征分类预测效果一览基本介绍研究内容程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于RBF-Adaboost数据分类预测&#xff08;Matlab完整程序和数据&#xff09; 2.多特征输入…...

编程日记 2023/9/14 8:42:06

【Java代码规范】阿里编码规约 VS CheckStyle

全文速览&#xff1a; 1、关于代码编码质量2、如何小成本有效管理企业内的编码规范 2.1 阿里编码规约IDE插件2.2 CheckStyle IDE插件 3、如何在代码提交中检验规范 3.1 阿里编码规约配置git precommit check3.2 CheckStyle配置git precommit check3.3 实践 1、关于代码编码质…...

编程日记 2023/9/14 8:41:06

iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标？

iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标&#xff1f; 1、在iPhone苹果手机上找到「设置」并点击打开&#xff1b; 2、在苹果iPhone设置内找到「辅助功能」并点击打开&#xff1b; 3、在苹果iPhone手机辅助功能内的动作交互内找到「触控」并点击打开&#xff1b…...

编程日记 2023/9/14 8:40:05

kibana报错内存溢出问题解决

一、背景&#xff1a; kibana内存溢出&#xff0c;进程被kill掉&#xff0c;导致前端页面访问不到。 报错内容 二、报错原因&#xff1a; 发现是前端 js 报的内存 oom 异常&#xff0c;通过网上资料发现node.js 的默认内存大小为1.4G Node 中通过 JavaScript 使用内存时只能…...

编程日记 2023/9/14 8:39:02

【C语法】1124循环结构

#include <stdio.h> int main(){ //输入一个数。倒叙输出各个位上的数。 //123456 6 5 4 3 2 1 // 1输出个位上的数 %10 // 2将这个数去掉个位上的数。 / 10 // 3当这个数最后变成0时结束 int a 0; printf("请输入一个正整数&#xff1a;"); scanf…...

编程日记 2023/9/14 8:38:02

在PHP8中向数组添加元素-PHP8知识详解

在php8中向数组添加元素有多种方法&#xff0c;在这里主要讲解几个常用的方法&#xff1a;使用方括号[]添加元素、使用array_unshift()函数&#xff0c;向数组的头部添加元素、使用array_push()函数&#xff0c;向数组的尾部添加元素、使用array_splice()函数添加元素。 1、使用…...

编程日记 2023/9/14 8:33:58

Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341

Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341 说明内容漏洞编号CVE-2019-6341漏洞名称Drupal XSS漏洞漏洞评级中危影响范围在7.65之前的Drupal 7版本中&#xff1b; 8.6.13之前的Drupal 8.6版本; 8.5.14之前的Drupal 8.5版本。漏洞描述Drupal诞生于2000年&#xff0c;是一…...

编程日记 2023/9/14 8:32:57

Pycharm中配置Celery启动

Pycharm中配置Celery启动 前置条件 目录结构 ----FerDemo --------celery_demo ------------tasks.py tasks.py文件代码 import sys import time from celery import Celeryapp Celery(demo,backendredis://:password127.0.0.1/0,brokerredis://:password127.0.0.1/1,broker…...

编程日记 2023/9/14 8:29:54

Jmeter —— 常用的几种断言方法（基本用法）

在使用JMeter进行性能测试或者接口自动化测试工作中&#xff0c;经常会用到的一个功能&#xff0c;就是断言&#xff0c;断言相当于检查点&#xff0c;它是用来判断系统返回的响应结果是否正确&#xff0c;以此帮我们判断测试是否通过&#xff0c;本文 主要介绍几种常用的断言&…...

编程日记 2023/9/14 8:27:52

mybatis bean属性识别丢失【NoSuchPropertyException】

背景 发现线上报错日志 org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.builder.BuilderException: Error evaluating expression Cause: org.apache.ibatis.ognl.NoSuchPropertyException: 参考 https://github.com/mybatis/mybatis-…...

编程日记 2023/9/14 8:25:50

点云从入门到精通技术详解100篇-基于补全点云与图像像素级融合的障碍物识别

目录 前言 感知融合技术研究现状及问题 感知融合技术概述 特征级融合研究现状...

编程日记 2023/9/14 8:21:47

如何做公司自己的网站首页/百度助手下载安装

2019独角兽企业重金招聘Python工程师标准>>> 最近有一个微信端要上&#xff0c;需要凌晨12点上线&#xff0c;不可能让我等到12点切流量吧&#xff0c;于是早早的配置好&#xff0c;回家睡觉 很简单&#xff0c;主要在nginx这层做点处理&#xff0c;就行了&#xff…...

编程日记 2025/1/8 2:07:39

wordpress的安装方法/网上推广app

Ajax辅助方法通过“Ajax”调用&#xff0c;如“Ajax.ActionLink”,"Ajax.BeginForm" 使用Ajax时&#xff0c;需要引入库文件 如Script文件夹中不存在jquery.unobtrusive-ajax.js时&#xff0c;可在NuGet程序包中安装&#xff1a; Ajax.ActionLink方法 可以创建一个…...

编程日记 2025/1/8 0:14:37

做外贸b2b网站/软文写作网站

概念 下载 安装 目录结构 启动 启动常遇到的问题 闪退 乱码 端口号被占用 关闭 1、直接点 X关闭 2、点击命令关闭 概念 Tomcat&#xff1a;Apache基金组织&#xff0c;中小型的JavaEE服务器&#xff0c;仅仅支持少量的JavaEE规范servlet/jsp。开源的&#xff0c;免…...

编程日记 2025/1/7 18:54:49

网站顶部固定怎么做/附近有学电脑培训班吗

为什么需要滑动窗口 常常有这样的需求&#xff1a;统计过去一段时间内的请求总数&#xff0c;过去一段时间内的平均值 这种需求用滑动窗口来实现相当适合 滑动窗口实现 本文介绍的实现基于go-zero的RollingWindow 数据结构 先不看具体的数据结构&#xff0c;想想滑动窗口应…...

编程日记 2025/1/7 18:48:43

网站建设用什么网站好一点/快速seo排名优化

HTML 元素 HTML 文档由 HTML 元素定义。 推荐分布式架构源码 HTML 元素 *开始标签常被称为起始标签&#xff08;opening tag&#xff09;&#xff0c;结束标签常称为闭合标签&#xff08;closing tag&#xff09;。 HTML 元素语法 HTML 元素以开始标签起始HTML 元素以结束标签…...

编程日记 2025/1/7 16:19:41

吴忠市建设局官方网站/网站开发合同

队列&#xff08;Queue&#xff09;&#xff1a;具有一定操作约束的线性表 插入和删除操作&#xff1a;只能在一端插入&#xff0c;而在另一端删除 先进先出 1、队列的顺序存储实现 队列的顺序存储结构通常由一个一维数组和一个记录队列头元素位置的变量front以及 一个记录队列…...

编程日记 2025/1/7 15:23:57