线性代数的本质(七)——特征值和特征向量
特征值和特征向量
本章特征值和特征向量的概念只在方阵的范畴内探讨。
相似矩阵
Grant:线性变换对应的矩阵依赖于所选择的基。
一般情况下,同一个线性变换在不同基下的矩阵不同。仍然以平面线性变换为例,Grant 选用标准坐标系下的基向量 i , j \mathbf i,\mathbf j i,j ,线性变换 T T T 对应的矩阵为 A A A ,而 Jennifer 使用另外一组基向量 i ′ , j ′ \mathbf i',\mathbf j' i′,j′ 。
我们已经知道矩阵 A A A 是追踪基向量 i , j \mathbf i,\mathbf j i,j 变换后的位置得到的,同样的线性变换在 i ′ , j ′ \mathbf i',\mathbf j' i′,j′ 下的表示,也需要追踪基向量 i ′ , j ′ \mathbf i',\mathbf j' i′,j′ 变换后的位置。具体过程如下:
对于 Jennifer 视角下的向量 v = [ x ′ y ′ ] \mathbf v=\begin{bmatrix} x' \\ y' \end{bmatrix} v=[x′y′]
- 同样的向量,用 Grant 的坐标系表示的坐标为 P [ x ′ y ′ ] P\begin{bmatrix} x' \\ y' \end{bmatrix} P[x′y′] ,其中 P P P 为基变换矩阵;
- 用 Grant 的语言描述变换后的向量 A P [ x ′ y ′ ] AP\begin{bmatrix} x' \\ y' \end{bmatrix} AP[x′y′]
- 将变换后的结果变回 Jennifer 的坐标系 P − 1 A P [ x ′ y ′ ] P^{-1}AP\begin{bmatrix} x' \\ y' \end{bmatrix} P−1AP[x′y′]
于是,我们得到同一个线性变换 T T T 在 Jennifer 的坐标系下对应的矩阵为 P − 1 A P P^{-1}AP P−1AP 。
这个结果暗示着数学上的转移作用,中间的矩阵 A A A 代表 Grant 坐标系下所见到的变换, P P P 和 P − 1 P^{-1} P−1 两个矩阵代表着转移作用(基变换矩阵),也就是在不同坐标系之间进行转换,实际上也是视角上的转化。 P − 1 A P P^{-1}AP P−1AP 仍然代表同一个变换,只不过是从别的坐标系的角度来看。
下面给出严格的数学证明。在线性空间 V V V 中取两组基,基变换公式为
( b 1 , b 2 , ⋯ , b n ) = ( a 1 , a 2 , ⋯ , a n ) P (\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)=(\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)P (b1,b2,⋯,bn)=(a1,a2,⋯,an)P 。
设线性变换 T T T 在这两组基下的矩阵分别为 A A A 和 B B B 。那么
T ( a 1 , a 2 , ⋯ , a n ) = ( a 1 , a 2 , ⋯ , a n ) A T ( b 1 , b 2 , ⋯ , b n ) = ( b 1 , b 2 , ⋯ , b n ) B T(\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)=(\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)A \\ T(\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)=(\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)B T(a1,a2,⋯,an)=(a1,a2,⋯,an)AT(b1,b2,⋯,bn)=(b1,b2,⋯,bn)B
取向量 v ∈ V \mathbf v\in V v∈V ,在两组基下的坐标向量分别为 x , x ′ \mathbf x,\mathbf x' x,x′,根据坐标变换公式有 x = P x ′ \mathbf x=P\mathbf x' x=Px′
T ( v ) = ( b 1 , b 2 , ⋯ , b n ) B x ′ = ( a 1 , a 2 , ⋯ , a n ) A x = ( b 1 , b 2 , ⋯ , b n ) P − 1 A P x ′ \begin{aligned} T(\mathbf v)&=(\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)B\mathbf x'\\ &=(\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)A\mathbf x \\ &=(\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)P^{-1}AP\mathbf x' \end{aligned} T(v)=(b1,b2,⋯,bn)Bx′=(a1,a2,⋯,an)Ax=(b1,b2,⋯,bn)P−1APx′
因为 b 1 , b 2 , ⋯ , b n \mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n b1,b2,⋯,bn 线性无关,所以
B = P − 1 A P B=P^{-1}AP B=P−1AP
因此, B B B 和 P − 1 A P P^{-1}AP P−1AP 表示同一种线性变换在不同基向量下的表示。
相似矩阵:设 A , B A,B A,B 都是 n n n 阶矩阵,若有 n n n 阶可逆矩阵 P P P ,使
B = P − 1 A P B=P^{-1}AP B=P−1AP
则称矩阵 A A A 与 B B B 相似(similar),记作 A ∼ B A\sim B A∼B。
用初等行变换计算相似矩阵:计算相似矩阵 P − 1 A P P^{-1}AP P−1AP 的一种有效方法是先计算 A P AP AP ,然后用行变换将增广矩阵 ( P ∣ A P ) (P\mid AP) (P∣AP) 化为 ( I ∣ P − 1 A P ) (I\mid P^{-1}AP) (I∣P−1AP),这样就不需要单独计算 P − 1 P^{-1} P−1了 。
特征值与特征向量
Grant:行列式告诉你一个变换对面积的缩放比例,特征向量则是在变换中保留在他所张成的空间中的向量,这两者都是暗含于空间中的性质,坐标系的选择并不会改变他们最根本的值。
我们已经知道,对角阵对于矩阵运算来说最为简单。若线性变换 T T T 在一组基下的矩阵为 A A A,为便于应用,自然考虑是否存在对角阵 Λ \Lambda Λ 和矩阵 A A A 相似,从而使用这种最简单的形式计算线性变换。
假设有对角阵 Λ ∼ A \Lambda\sim A Λ∼A,即存在可逆矩阵 P P P ,使得
P − 1 A P = Λ = diag ( λ 1 , λ 2 , ⋯ , λ n ) P^{-1}AP=\Lambda=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n) P−1AP=Λ=diag(λ1,λ2,⋯,λn)
将矩阵 P P P 按列分块 P = ( x 1 , x 2 , ⋯ , x n ) P=(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n) P=(x1,x2,⋯,xn) ,则上式等价于
A ( x 1 , x 2 , ⋯ , x n ) = ( x 1 , x 2 , ⋯ , x n ) Λ A(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n)=(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n)\Lambda A(x1,x2,⋯,xn)=(x1,x2,⋯,xn)Λ
按分块矩阵的乘法,上式可写成
A x 1 = λ 1 x 1 A x 2 = λ 1 x 2 ⋯ A x n = λ n x n A\mathbf x_1=\lambda_1\mathbf x_1\\ A\mathbf x_2=\lambda_1\mathbf x_2\\ \cdots\\ A\mathbf x_n=\lambda_n\mathbf x_n Ax1=λ1x1Ax2=λ1x2⋯Axn=λnxn
根据假定 P P P 可逆,其列向量非零,因此我们希望找到符合条件的 λ j , x j \lambda_j,\mathbf x_j λj,xj。
定义:对于矩阵 A A A ,如果存在数 λ \lambda λ 和非零向量 u \mathbf u u,使得
A u = λ u A\mathbf u=\lambda\mathbf u Au=λu
则称 λ \lambda λ 是矩阵 A A A 的一个特征值(eigenvalue), u \mathbf u u 是特征值 λ \lambda λ 的一个特征向量(eigenvector)。
(1) 特征向量必须是非零向量;
(2) 特征值和特征向量是相伴出现的。
事实上,对于任意非零常数 c c c, c u c\mathbf u cu 都是特征值 λ \lambda λ 的特征向量,这是因为
if A u = λ u , then A ( c u ) = λ ( c u ) \text{if }A\mathbf u=\lambda\mathbf u,\text{ then }A(c\mathbf u)=\lambda (c\mathbf u) if Au=λu, then A(cu)=λ(cu)
由于矩阵和线性变换是一一对应的,我们可以借助几何直观理解这个定义。
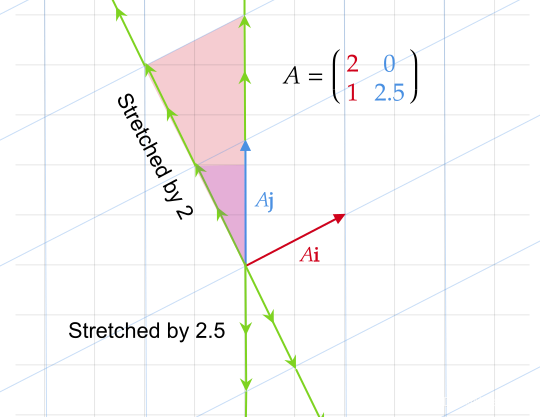
- 特征向量在变换过程中只受到拉伸或者压缩
- 特征值描述对应特征向量经过线性变换后的缩放程度
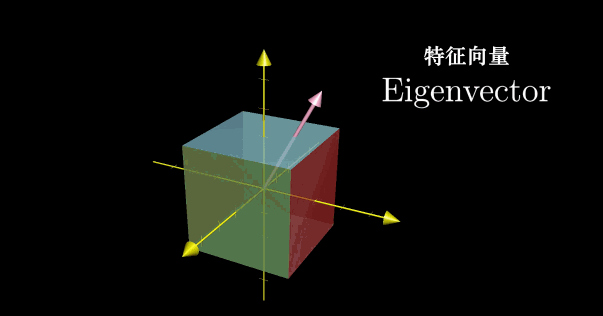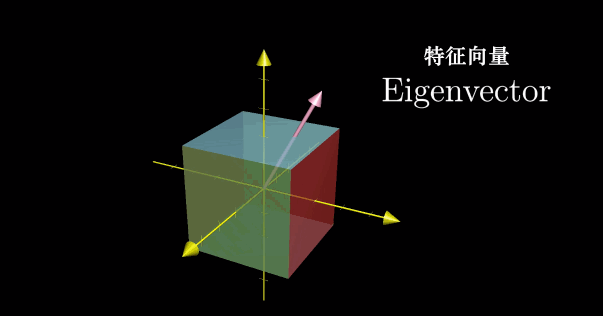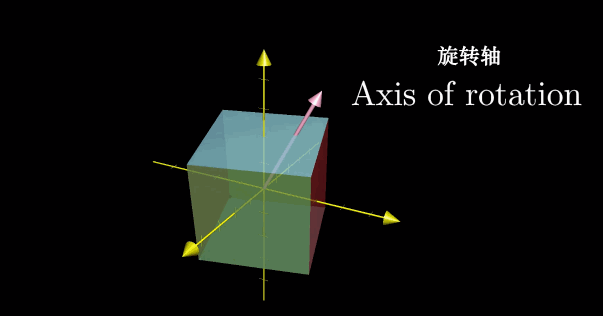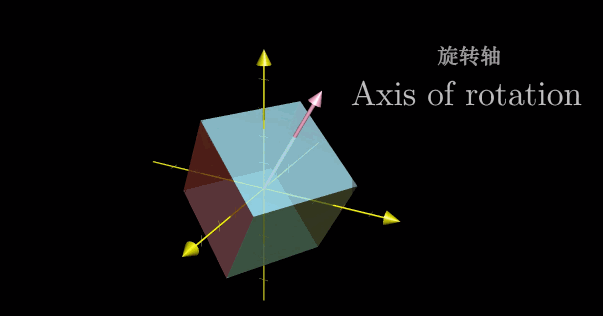
对于三维空间中的旋转,如果能够找到对应的特征向量,也即能够留在它所张成的空间中的向量,那么就意味着我们找到了旋转轴。特别地,这就意味着将一个三维旋转看成绕这个特征向量旋转一定角度,要比考虑相应的矩阵变换要直观。此时对应的特征值为1,因为旋转并不改变任何一个向量,所以向量的长度保持不变。
由定义知道,求解特征向量就是寻找非零向量 u \mathbf u u 使得
( A − λ I ) u = 0 (A-\lambda I)\mathbf u=0 (A−λI)u=0
显然, u = 0 \mathbf u=0 u=0 时恒成立,但是我们要寻找的是非零解。 齐次矩阵方程有非零解的充分必要条件是系数矩阵的行列式为零,即
det ( A − λ I ) = 0 \det(A-\lambda I)=0 det(A−λI)=0
也就是系数矩阵所代表的线性变换将空间压缩到更低的维度。上式称为矩阵 A A A 的特征方程(characteristic equation)。矩阵 A A A 的特征值就是它的特征方程的根。
多项式
f ( λ ) = det ( A − λ I ) f(\lambda)=\det(A-\lambda I) f(λ)=det(A−λI)
称为矩阵 A A A 的特征多项式(characteristic polynomial)。
由上面的讨论可以得出求 n n n阶矩阵 A A A的特征值与特征向量的简要步骤:
- 求出 A A A 的特征多项式,即计算 n n n阶行列式 det ( A − λ I ) \det(A-\lambda I) det(A−λI);
- 求解特征方程 det ( A − λ I ) = 0 \det(A-\lambda I)=0 det(A−λI)=0 ,得到 n n n个根,即为 A A A的 n n n 个特征值;
- 对求得的每个特征值 λ i \lambda_i λi 分别带入 ( A − λ I ) x = 0 (A-\lambda I)\mathbf x=0 (A−λI)x=0 求其非零解,便是对应的特征向量。
示例:求矩阵 A = [ 1 2 3 2 ] A=\begin{bmatrix}1&2\\3&2\end{bmatrix} A=[1322] 的特征值和特征向量。
解: A A A 的特征多项式为
det ( A − λ I ) = ∣ 1 − λ 2 3 2 − λ ∣ = λ 2 − 3 λ − 4 = ( λ − 4 ) ( λ + 1 ) \begin{aligned}\det(A-\lambda I)&=\begin{vmatrix}1-\lambda&2\\3&2-\lambda\end{vmatrix} \\ &=\lambda^2-3\lambda-4=(\lambda-4)(\lambda+1) \end{aligned} det(A−λI)= 1−λ322−λ =λ2−3λ−4=(λ−4)(λ+1)
因此 A A A 的特征值为 λ 1 = 4 , λ 2 = − 1 \lambda_1=4,\lambda_2=-1 λ1=4,λ2=−1。
将 λ 1 = 4 \lambda_1=4 λ1=4 带入矩阵方程 ( A − λ I ) x = 0 (A-\lambda I)\mathbf x=0 (A−λI)x=0 ,有
[ − 3 2 3 − 2 ] [ x 1 x 2 ] = 0 [ − 3 2 3 − 2 ] → [ 3 − 2 0 0 ] \begin{bmatrix}-3&2\\3&-2\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=0 \\ \begin{bmatrix}-3&2\\3&-2\end{bmatrix}\to\begin{bmatrix}3&-2\\0&0\end{bmatrix} [−332−2][x1x2]=0[−332−2]→[30−20]
求得特征值 λ 1 = 4 \lambda_1=4 λ1=4 对应的一个特征向量 u 1 = c [ 2 3 ] \mathbf u_1=c\begin{bmatrix}2\\3\end{bmatrix} u1=c[23]
将 λ 1 = − 1 \lambda_1=-1 λ1=−1 带入矩阵方程 ( A − λ I ) x = 0 (A-\lambda I)\mathbf x=0 (A−λI)x=0 ,有
[ 2 2 3 3 ] [ x 1 x 2 ] = 0 [ 2 2 3 3 ] → [ 1 1 0 0 ] \begin{bmatrix}2&2\\3&3\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=0 \\ \begin{bmatrix}2&2\\3&3\end{bmatrix}\to\begin{bmatrix}1&1\\0&0\end{bmatrix} [2323][x1x2]=0[2323]→[1010]
求得特征值 λ 2 = − 1 \lambda_2=-1 λ2=−1 对应的特征向量 u 2 = c [ − 1 1 ] \mathbf u_2=c\begin{bmatrix}-1\\1\end{bmatrix} u2=c[−11]
性质:
- 相似矩阵(同样的线性变换)有相同的特征多项式,从而有相同的特征值;
- 矩阵 A A A 与其转置矩阵 A T A^T AT 有相同的特征值;
- 属于矩阵不同特征值的特征向量线性无关;
- 矩阵的所有特征值之和等于其主对角线元素之和(矩阵的迹);
- 矩阵的所有特征值之积等于矩阵的行列式;
- 三角阵的特征值是其主对角线元素;
- 矩阵乘积 A B AB AB 和 B A BA BA 具有相同的非零特征值
证明:(性质1)设 A ∼ B A\sim B A∼B,即 B = P − 1 A P B=P^{-1}AP B=P−1AP ,于是
det ( B − λ I ) = det ( P − 1 ( A − λ I ) P ) = det ( P − 1 ) det ( A − λ I ) det ( P ) = det ( A − λ I ) \begin{aligned} \det(B-\lambda I)&=\det(P^{-1}(A-\lambda I)P) \\ &=\det(P^{-1})\det(A-\lambda I)\det(P) \\ &=\det(A-\lambda I) \\ \end{aligned} det(B−λI)=det(P−1(A−λI)P)=det(P−1)det(A−λI)det(P)=det(A−λI)
故 A A A 与 B B B 有相同的特征多项式,从而有相同的特征值
(性质4)设 n n n阶矩阵 A A A 的特征值为 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn。由于矩阵的特征值就是其特征方程的根,从而
f ( λ ) = det ( A − λ I ) = ( λ 1 − λ ) ( λ 2 − λ ) ⋯ ( λ n − λ ) f(\lambda)=\det(A-\lambda I)=(\lambda_1-\lambda)(\lambda_2-\lambda)\cdots(\lambda_n-\lambda) f(λ)=det(A−λI)=(λ1−λ)(λ2−λ)⋯(λn−λ)
上式取 λ = 0 \lambda=0 λ=0 ,有 f ( 0 ) = det A = λ 1 λ 2 ⋯ λ n f(0)=\det A=\lambda_1\lambda_2\cdots\lambda_n f(0)=detA=λ1λ2⋯λn
(性质7)假设矩阵 A A A 与 B B B 分别是 m × n m\times n m×n 与 n × m n\times m n×m 矩阵。
证法1:设 λ \lambda λ 是 A B AB AB 的任一非零特征值, u \mathbf u u 是这一特征值的特征向量,则 ( A B ) u = λ u (AB)\mathbf u=\lambda\mathbf u (AB)u=λu ,等式两边同时左乘 B B B 有
( B A ) ( B u ) = λ ( B u ) (BA)(B\mathbf u)=\lambda(B\mathbf u) (BA)(Bu)=λ(Bu)
又由于 A B u = λ u ≠ 0 AB\mathbf u=\lambda\mathbf u\neq0 ABu=λu=0 可知 B u ≠ 0 B\mathbf u\neq 0 Bu=0 。所以 B u B\mathbf u Bu 是 B A BA BA 关于特征值 λ \lambda λ 的特征向量。这也证明了 λ \lambda λ 也是 B A BA BA 的特征值。
同理可证 B A BA BA 的非零特征值也是 A B AB AB 的特征值。这就证明了 A B AB AB 和 B A BA BA 具有相同的非零特征值。
证法2:易知
[ I m − A O I n ] [ A B O B O ] [ I m A O I n ] = [ O O B A B ] \begin{bmatrix}I_m&-A\\O&I_n\end{bmatrix} \begin{bmatrix}AB&O\\B&O\end{bmatrix} \begin{bmatrix}I_m&A\\O&I_n\end{bmatrix}= \begin{bmatrix}O&O\\B&AB\end{bmatrix} [ImO−AIn][ABBOO][ImOAIn]=[OBOAB]
又由于
[ I m − A O I n ] [ I m A O I n ] = I m + n \begin{bmatrix}I_m&-A\\O&I_n\end{bmatrix} \begin{bmatrix}I_m&A\\O&I_n\end{bmatrix}= I_{m+n} [ImO−AIn][ImOAIn]=Im+n
可知
[ A B O B O ] ∼ [ O O B B A ] \begin{bmatrix}AB&O\\B&O\end{bmatrix}\sim \begin{bmatrix}O&O\\B&BA\end{bmatrix} [ABBOO]∼[OBOBA]
它们有相同的特征多项式,即
λ n det ( λ I m − A B ) = λ m det ( λ I n − B A ) \lambda^n\det(\lambda I_m-AB)=\lambda^m\det(\lambda I_n-BA) λndet(λIm−AB)=λmdet(λIn−BA)
上式称为Sylvester降幂公式。这里表明, A B AB AB 和 B A BA BA 的只相差了个 m − n m-n m−n 个零特征值,其余非零特征值相同。
特征基与对角化
由上节知道,特征值和特征向量定义的初衷是为了线性变换的相似对角化,即
P − 1 A P = Λ P^{-1}AP=\Lambda P−1AP=Λ
由定义的推理知道,矩阵 A A A 的每个特征向量就是 P P P 的一个列向量,而 P P P 是矩阵 A A A 的基向量到对角阵 Λ \Lambda Λ 基向量的过渡矩阵。过渡矩阵 P P P 也可看作对角阵 Λ \Lambda Λ 的基向量组在矩阵 A A A 基向量下的坐标,所以对基向量的限制条件也适用于特征向量组。
定理:矩阵 A n A_n An 可以相似对角化的充要条件是 A n A_n An 有 n n n 个线性无关的特征向量。此时,对角元素就是对应的特征值。
设矩阵 A A A的特征值与特征向量对应关系 A u 1 = λ 1 u 1 , A u 2 = λ 2 u 2 A\mathbf u_1=\lambda_1\mathbf u_1,\quad A\mathbf u_2=\lambda_2\mathbf u_2 Au1=λ1u1,Au2=λ2u2 ,令 P = [ u 1 , u 2 ] P=[\mathbf u_1,\mathbf u_2] P=[u1,u2]
A P = [ λ 1 u 1 , λ 2 u 2 ] = [ u 1 , u 2 ] [ λ 1 0 0 λ 2 ] = P Λ AP=[\lambda_1\mathbf u_1,\lambda_2\mathbf u_2]= [\mathbf u_1,\mathbf u_2] \begin{bmatrix} \lambda_1&0 \\ 0&\lambda_2 \end{bmatrix}= P\Lambda \\ AP=[λ1u1,λ2u2]=[u1,u2][λ100λ2]=PΛ
若 P P P 可逆,即 u 1 , u 2 \mathbf u_1,\mathbf u_2 u1,u2 线性无关,则
Λ = P − 1 A P = [ λ 1 0 0 λ 2 ] \Lambda=P^{-1}AP=\begin{bmatrix} \lambda_1&0 \\ 0&\lambda_2 \end{bmatrix} Λ=P−1AP=[λ100λ2]
当特征向量的数量足够多时,这些特征向量就可以构成特征基(eigenbasis)。在特征基坐标系角度看,同一个线性变换只是伸缩变换(对角阵)。
特征基的坐标使用的是矩阵 A A A 的基向量。
例:尝试将下列矩阵对角化
A = [ 1 3 3 − 3 − 5 − 3 3 3 1 ] A=\begin{bmatrix} 1&3&3 \\ -3&-5&-3 \\ 3&3&1 \end{bmatrix} A= 1−333−533−31
解:对角化工作可分为4步来完成
step 1:求出特征值。矩阵 A A A 的特征方程为
det ( A − λ I ) = − ( λ − 1 ) ( λ + 2 ) 2 \det(A-\lambda I)=-(\lambda-1)(\lambda+2)^2 det(A−λI)=−(λ−1)(λ+2)2
特征值是 λ = 1 \lambda=1 λ=1 和 λ = − 2 \lambda=-2 λ=−2
step 2:求出线性无关的特征向量。对于 λ = 1 \lambda=1 λ=1 的特征向量 u 1 = ( 1 , − 1 , 1 ) T \mathbf u_1=(1,-1,1)^T u1=(1,−1,1)T
对于 λ = − 2 \lambda=-2 λ=−2 的特征向量 u 2 = ( − 1 , 1 , 0 ) T \mathbf u_2=(-1,1,0)^T u2=(−1,1,0)T 和 u 3 = ( − 1 , 0 , 1 ) T \mathbf u_3=(-1,0,1)^T u3=(−1,0,1)T
可以验证 u 1 , u 2 , u 3 \mathbf u_1,\mathbf u_2,\mathbf u_3 u1,u2,u3 是线性无关的。
step 3:使用特征向量构造过渡矩阵(向量的次序不重要)
P = [ 1 − 1 − 1 − 1 1 0 1 0 1 ] P=\begin{bmatrix} 1&-1&-1 \\ -1&1&0 \\ 1&0&1 \end{bmatrix} P= 1−11−110−101
step 4:使用对应的特征值构造对角阵(特征值的次序必须和矩阵 P P P的列选择的特征向量的次序一致)
Λ = [ 1 0 0 0 − 2 0 0 0 − 2 ] \Lambda=\begin{bmatrix} 1&0&0 \\ 0&-2&0 \\ 0&0&-2 \end{bmatrix} Λ= 1000−2000−2
可简单验证 A P = P Λ AP=P\Lambda AP=PΛ,这等价于验证当 P P P 可逆时 Λ = P − 1 A P \Lambda=P^{-1}AP Λ=P−1AP 。
一些常见变换的特征值与特征向量列举如下:
(1) 等比例缩放变换 [ k 0 0 k ] \begin{bmatrix}k &0\\0 &k\end{bmatrix} [k00k] 的特征多项式为 ( λ − k ) 2 (\lambda-k)^2 (λ−k)2 ,有两个相等的特征值 λ = k \lambda=k λ=k ,但平面内任意非零向量都属于这个特征值的特征向量。
(2) 普通缩放变换 [ k 1 0 0 k 2 ] \begin{bmatrix}k_1 &0\\0 &k_2\end{bmatrix} [k100k2] 的特征多项式为 ( λ − k 1 ) ( λ − k 2 ) (\lambda-k_1)(\lambda-k_2) (λ−k1)(λ−k2) ,有两个特征值 λ 1 = k 1 , λ 2 = k 2 \lambda_1=k_1,\lambda_2=k_2 λ1=k1,λ2=k2 ,特征向量分别为 u 1 = [ 1 0 ] , u 2 = [ 0 1 ] \mathbf u_1=\begin{bmatrix}1\\0\end{bmatrix},\mathbf u_2=\begin{bmatrix}0\\1\end{bmatrix} u1=[10],u2=[01]。
(3) 旋转变换 [ cos θ − sin θ sin θ cos θ ] \begin{bmatrix}\cos\theta &-\sin\theta\\ \sin\theta &\cos\theta\end{bmatrix} [cosθsinθ−sinθcosθ] 的特征多项式为 λ 2 + 2 λ cos θ + 1 \lambda^2+2\lambda\cos\theta+1 λ2+2λcosθ+1 ,有两个复特征值 λ 1 = cos θ + i sin θ , λ 2 = cos θ − i sin θ \lambda_1=\cos\theta+i\sin\theta,\lambda_2=\cos\theta-i\sin\theta λ1=cosθ+isinθ,λ2=cosθ−isinθ ,对应两个复特征向量 u 1 = [ 1 − i ] , u 2 = [ 1 i ] \mathbf u_1=\begin{bmatrix}1\\-i\end{bmatrix},\mathbf u_2=\begin{bmatrix}1\\i\end{bmatrix} u1=[1−i],u2=[1i]。
值得注意的是,特征值出现虚数的情况一般对应于变换中的某一种旋转。
(4) 水平剪切变换 [ 1 k 0 1 ] \begin{bmatrix}1 &k\\0 &1\end{bmatrix} [10k1] 的特征多项式为 ( λ − 1 ) 2 (\lambda-1)^2 (λ−1)2 ,有两个相等的特征值 λ = 1 \lambda=1 λ=1 ,只有一个特征向量 u 1 = [ 1 0 ] \mathbf u_1=\begin{bmatrix}1\\0\end{bmatrix} u1=[10] ,不能张成整个平面。
特征向量的应用
许多实际问题都可归结为研究矩阵的方幂 A n ( n ∈ N ∗ ) A^n\quad (n\in\N^*) An(n∈N∗) 乘以向量 v \mathbf v v ,不难想象,当方幂很大时,直接用矩阵的乘法、矩阵与向量的乘法进行计算会非常麻烦。而矩阵的特征值和特征向量矩阵对幂运算十分友好,因此在数学和实际问题中有着广泛的应用。
性质:
-
设矩阵 A A A 特征值 λ \lambda λ 的特征向量为 u \mathbf u u,则用数学归纳法可以得到
A n u = λ n u A^n\mathbf u=\lambda^n\mathbf u Anu=λnu -
设矩阵 A A A 特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2 的特征向量分别为 u 1 , u 2 \mathbf u_1,\mathbf u_2 u1,u2。对于任意向量 v \mathbf v v ,可以用特征向量线性表示 v = v 1 u 1 + v 2 u 2 \mathbf v=v_1\mathbf u_1+v_2\mathbf u_2 v=v1u1+v2u2 。那么,用数学归纳法可以得到
A n v = v 1 λ 1 n u 1 + v 2 λ 2 n u 2 A^n\mathbf v=v_1\lambda_1^n\mathbf u_1+v_2\lambda_2^n\mathbf u_2 Anv=v1λ1nu1+v2λ2nu2
证明:从线性变换的角度理解,性质1中矩阵 A A A 只是对特征向量做伸缩变换,因此矩阵幂的效果等价于特征值(缩放比例)的幂。性质2中矩阵的幂变换等同于切换到特征基中做了同等次数的伸缩变换。
性质1用数学归纳法证明:
(1) 当 n = 1 n=1 n=1 时
A u = λ u A\mathbf u=\lambda\mathbf u Au=λu
(2) 假设当 n = k − 1 n=k-1 n=k−1 时成立,即
A k − 1 u = λ k − 1 u A^{k-1}\mathbf u=\lambda^{k-1}\mathbf u Ak−1u=λk−1u
当 n = k n=k n=k 时,因为
A k u = A ( A k − 1 u ) = A ( λ k − 1 u ) = λ k − 1 ( A u ) = λ k u A^k\mathbf u=A(A^{k-1}\mathbf u)=A(\lambda^{k-1}\mathbf u)=\lambda^{k-1}(A\mathbf u)=\lambda^k\mathbf u Aku=A(Ak−1u)=A(λk−1u)=λk−1(Au)=λku
所以,对 n = k n=k n=k 时成立。由数学归纳法可知,对所有的 n ∈ N ∗ n\in\N^* n∈N∗ 都成立。
实例:在扩散理论中的应用。设某物质能以气态和液态的混合状态存在,假定在任意一段很短的时间内
(1) 液体的 5 % 5\% 5% 蒸发成气态;
(2) 气体的 1 % 1\% 1% 凝结成液态。
假定该物质的总量一直保持不变,那么最终的情况如何?
为了研究的方便,用 g 0 , l 0 g_0,l_0 g0,l0 分别表示现在的气体和液体的比例 ( g 0 + l 0 = 1 ) (g_0+l_0=1) (g0+l0=1), g n , l n g_n,l_n gn,ln 分别表示 n n n 段时间后液体和气体的比例。记物质总量为 M M M ,一直保持不变。
(1) 先求 g 1 , l 1 g_1,l_1 g1,l1
可以看出,在很短时间后,气体由现在气体的 99 % 99\% 99% 加上现在液体的 5 % 5\% 5% 组成,即
g 1 M = 0.99 g 0 M + 0.05 l 0 M g_1M=0.99g_0M+0.05l_0M g1M=0.99g0M+0.05l0M
同理,在很短时间后的液体
l 1 M = 0.01 g 0 M + 0.95 l 0 M l_1M=0.01g_0M+0.95l_0M l1M=0.01g0M+0.95l0M
因此
{ g 1 = 0.99 g 0 + 0.05 l 0 l 1 = 0.01 g 0 + 0.95 l 0 \begin{cases} g_1=0.99g_0+0.05l_0 \\ l_1=0.01g_0+0.95l_0 \end{cases} {g1=0.99g0+0.05l0l1=0.01g0+0.95l0
矩阵形式为
[ g 1 l 1 ] = [ 0.99 0.05 0.01 0.95 ] [ g 0 l 0 ] \begin{bmatrix} g_1\\l_1 \end{bmatrix}= \begin{bmatrix} 0.99&0.05\\0.01&0.95 \end{bmatrix} \begin{bmatrix} g_0\\l_0 \end{bmatrix} [g1l1]=[0.990.010.050.95][g0l0]
记矩阵 P = [ 0.99 0.05 0.01 0.95 ] P=\begin{bmatrix} 0.99&0.05\\0.01&0.95 \end{bmatrix} P=[0.990.010.050.95] 则上式写为
[ g 1 l 1 ] = P [ g 0 l 0 ] \begin{bmatrix} g_1\\l_1 \end{bmatrix}=P\begin{bmatrix} g_0\\l_0 \end{bmatrix} [g1l1]=P[g0l0]
矩阵 P P P 记录了很短时间内气液的转变情况。
(2) 类似与 g 1 , l 1 g_1,l_1 g1,l1 的推导过程,可以得到
[ g 1 l 1 ] = P [ g 0 l 0 ] ; [ g 2 l 2 ] = P [ g 1 l 1 ] = P 2 [ g 0 l 0 ] ; ⋯ ⋯ [ g n l n ] = P [ g n − 1 l n − 1 ] = P n [ g 0 l 0 ] \begin{aligned} & \begin{bmatrix} g_1\\l_1 \end{bmatrix}=P\begin{bmatrix} g_0\\l_0 \end{bmatrix}; \\ & \begin{bmatrix} g_2\\l_2 \end{bmatrix}=P\begin{bmatrix} g_1\\l_1 \end{bmatrix}=P^2\begin{bmatrix} g_0\\l_0 \end{bmatrix}; \\ & \cdots\cdots \\ & \begin{bmatrix} g_n\\l_n \end{bmatrix}=P\begin{bmatrix} g_{n-1}\\l_{n-1} \end{bmatrix}=P^n\begin{bmatrix} g_0\\l_0 \end{bmatrix} \end{aligned} [g1l1]=P[g0l0];[g2l2]=P[g1l1]=P2[g0l0];⋯⋯[gnln]=P[gn−1ln−1]=Pn[g0l0]
由于该问题已转化为矩阵指数的形式,我们可以用矩阵特征值和特征向量的性质求解。
(3) 可以证明矩阵
A = [ 1 − p q p 1 − q ] ( 0 < p , q < 1 ) A=\begin{bmatrix}1-p & q\\ p &1-q\end{bmatrix}\quad (0<p,q<1) A=[1−ppq1−q](0<p,q<1)
的特征值是 λ 1 = 1 , λ 2 = 1 − p − q \lambda_1=1,\ \lambda_2=1-p-q λ1=1, λ2=1−p−q,对应的特征向量分别是 u 1 = [ q p ] , u 2 = [ 1 − 1 ] \mathbf u_1=\begin{bmatrix} q\\ p\end{bmatrix},\ \mathbf u_2=\begin{bmatrix} 1\\ -1\end{bmatrix} u1=[qp], u2=[1−1]。
从而得到矩阵 P P P 的特征值是 λ 1 = 1 , λ 2 = 0.94 \lambda_1=1,\ \lambda_2=0.94 λ1=1, λ2=0.94,对应的特征向量分别是 u 1 = [ 0.05 0.01 ] , u 2 = [ 1 − 1 ] \mathbf u_1=\begin{bmatrix} 0.05\\ 0.01\end{bmatrix},\ \mathbf u_2=\begin{bmatrix} 1\\ -1\end{bmatrix} u1=[0.050.01], u2=[1−1]。再把初始向量 [ g 0 l 0 ] \begin{bmatrix} g_0\\l_0 \end{bmatrix} [g0l0] 用特征向量表示,设
[ g 0 l 0 ] = k 1 [ 0.05 0.01 ] + k 2 [ 1 − 1 ] where g 0 + l 0 = 1 \begin{bmatrix} g_0\\l_0 \end{bmatrix}=k_1\begin{bmatrix} 0.05\\ 0.01\end{bmatrix}+k_2\begin{bmatrix} 1\\ -1\end{bmatrix}\quad\text{where }g_0+l_0=1 [g0l0]=k1[0.050.01]+k2[1−1]where g0+l0=1
解得 k 1 = 50 3 , k 2 = g 0 − 5 6 k_1=\frac{50}{3},k_2=g_0-\frac{5}{6} k1=350,k2=g0−65 ,所以由性质2得,对于任意的自然数 n n n 有
[ g n l n ] = P n [ g 0 l 0 ] = k 1 × 1 n [ 0.05 0.01 ] + k 2 × 0.9 4 n [ 1 − 1 ] \begin{bmatrix} g_n\\l_n \end{bmatrix}=P^n\begin{bmatrix} g_0\\l_0 \end{bmatrix}=k_1\times1^n\begin{bmatrix} 0.05\\ 0.01\end{bmatrix}+k_2\times0.94^n\begin{bmatrix} 1\\ -1\end{bmatrix} [gnln]=Pn[g0l0]=k1×1n[0.050.01]+k2×0.94n[1−1]
从而 g n = 0.05 k 1 + 0.9 4 n k 2 , l n = 0.01 k 1 − 0.9 4 n k 2 g_n=0.05k_1+0.94^nk_2,\ l_n=0.01k_1-0.94^nk_2 gn=0.05k1+0.94nk2, ln=0.01k1−0.94nk2,所以
g ∞ = lim n → ∞ ( 0.05 k 1 + 0.9 4 n k 2 ) = 0.05 k 1 = 5 6 l ∞ = lim n → ∞ ( 0.01 k 1 − 0.9 4 n k 2 ) = 0.01 k 1 = 1 6 g_{\infty}=\lim\limits_{n\to\infty}(0.05k_1+0.94^nk_2)=0.05k_1=\frac{5}{6} \\ l_{\infty}=\lim\limits_{n\to\infty}(0.01k_1-0.94^nk_2)=0.01k_1=\frac{1}{6} g∞=n→∞lim(0.05k1+0.94nk2)=0.05k1=65l∞=n→∞lim(0.01k1−0.94nk2)=0.01k1=61
那么,我们可以得到,不管该物质最初的气液比率如何,最终将达到一个平衡状态,此时该物质的 5 / 6 5/6 5/6 是气态的, 1 / 6 1/6 1/6 是液体的。
相关文章:

线性代数的本质(七)——特征值和特征向量
特征值和特征向量 本章特征值和特征向量的概念只在方阵的范畴内探讨。 相似矩阵 Grant:线性变换对应的矩阵依赖于所选择的基。 一般情况下,同一个线性变换在不同基下的矩阵不同。仍然以平面线性变换为例,Grant 选用标准坐标系下的基向量 i…...

c语言进阶部分详解(指针初阶)
大家好!,前段时间一直在准备数学建模竞赛,现在也是忙完了。抓紧继续给大家带来c语言的内容。今天给大家带来指针初阶部分的讲解 当我们谈论C语言中的指针时,实际上是在讨论一种非常重要的概念,因为指针是C语言的核心之…...

Socks5代理IP在跨境电商与网络游戏中的网络安全应用
在数字化时代,跨境电商和网络游戏已成为全球网络世界中的两大热门领域。然而,这两者都面临着相似的网络安全挑战,需要高效的网络代理来解决。本文将讨论Socks5代理IP在跨境电商和网络游戏中的关键作用,以及如何通过这一技术增强网…...
Gin框架---基础综述
目录 一:经典入门案例二:请求参数2.1: API参数2.2: URL参数2.3: 表单参数 三: 响应参数四:数据解析和绑定4.1: JSON数据解析绑定4.2: FROM表单数据解析和绑定 五: 路由组六:异步处理七:中间件7.…...

排序算法-快速排序
属性 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元 素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有 …...
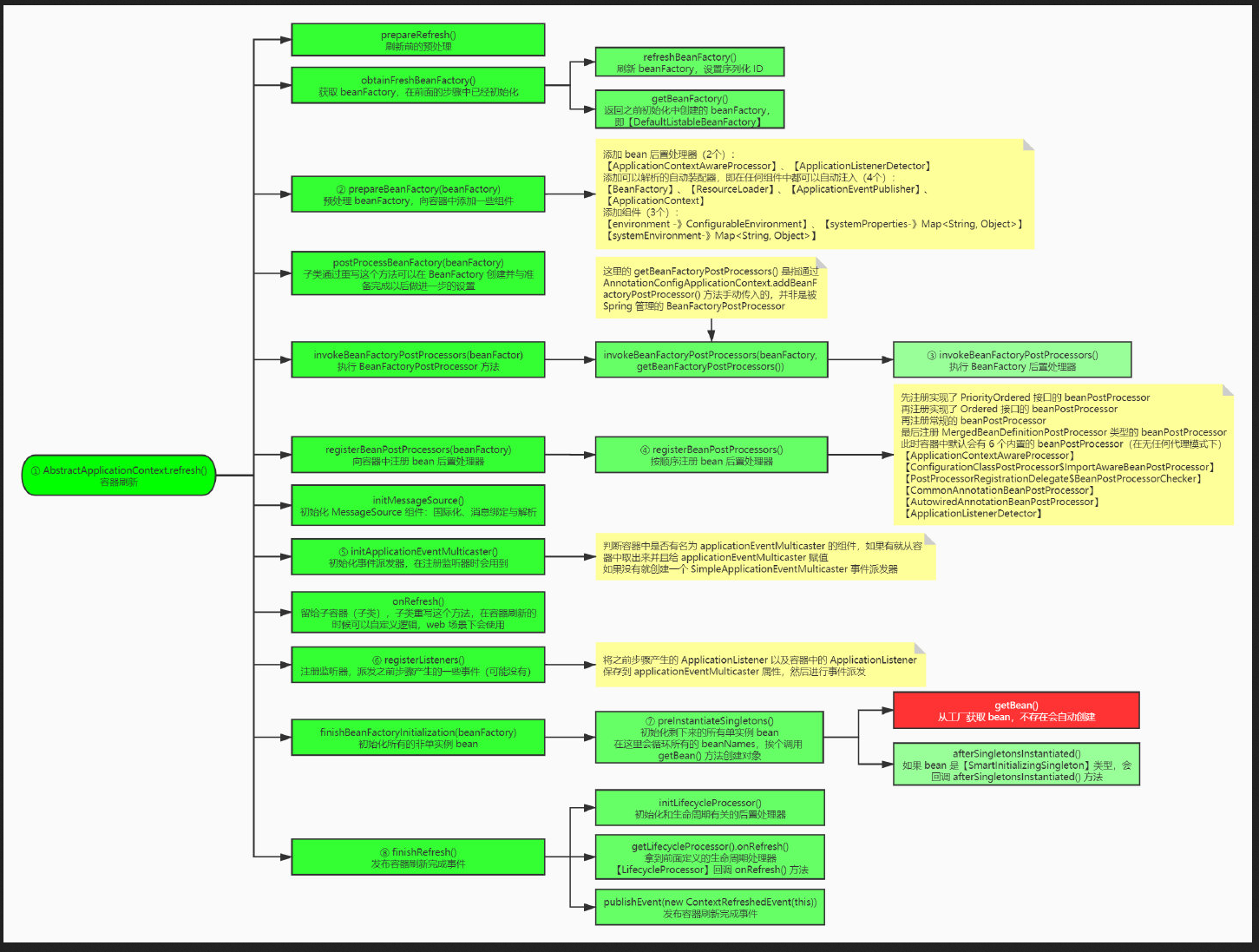
【Spring容器的启动过程】
Spring容器的启动过程 Spring 在初始化过程中有二个非常重要的步骤,容器的初始化与刷新。 初始化流程 如果想生成 bean 对象,那么就需要一个 beanFactory 工厂(DefaultListableBeanFactory)如果想让加了特定注解(如 …...

普通二本+转专业学计算机是什么感受
目录 自我介绍转入前为什么转专业为什么转入机械专业 转入后转入后感受确定自学计算机自学计算机的时间分配 自我介绍 作者现在是大二,由于当时高考考砸了,分数在重本线左右,为了去一个稍微好一点的学校,于是填报了化学工程与工艺(并不是说这专业不好,只是填报化工更容易进这个…...

力扣1、两数之和
转到力扣 题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可…...
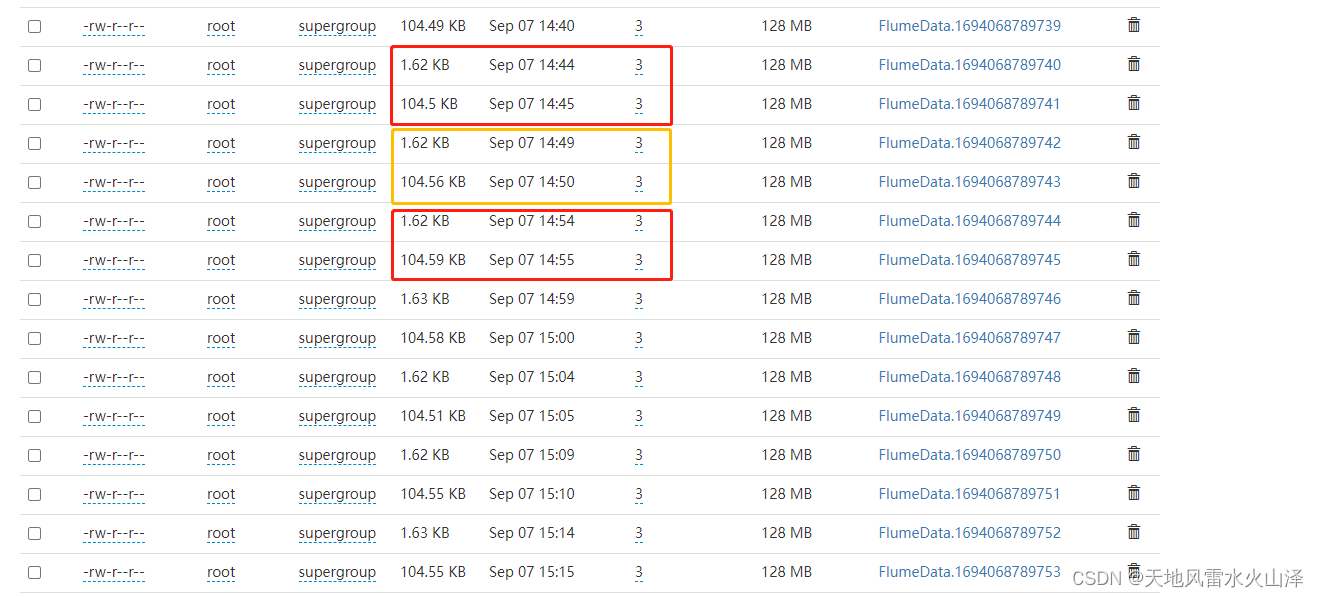
一百七十三、Flume——Flume写入HDFS后的诸多小文件问题
一、目的 在用Flume采集Kafka中的数据写入HDFS后,发现写入HDFS的不是每天一个文件,而是一个文件夹,里面有很多小文件,浪费namenode的宝贵资源 二、Flume的配置文件优化(参考了其他博文) (一&a…...

Android.mk中C++使用
参考: https://gerrit.twrp.me/c/android_bootable_recovery//4366/1/Android.mk ifeq ($(BOARD_USES_RECOVERY_AS_BOOT), true) LOCAL_CFLAGS -DBOARD_USES_RECOVERY_AS_BOOT endif ifeq ($(BOARD_BUILD_SYSTEM_ROOT_IMAGE), true) LOCAL_CFLAGS -DBOA…...
K8S:Pod概念、分类及相关的策略
文章目录 一.pod相关概念1.Pod基础概念2.Kubrenetes集群中Pod两种使用方式3.pause容器的Pod中的所有容器共享的资源4.kubernetes中的pause容器主要为每个容器提供功能:5.Kubernetes设计这样的Pod概念和特殊…...

【Java杂谈】#1 【MCA JAVA后端架构师】
文章目录 巧用弱引用 解决 TreadLocal内存泄漏问题P5,P6,P7Spring 巧用弱引用 解决 TreadLocal内存泄漏问题 < Treadlocal > 本地调用框架使用(Spring) IOC,AOP注解transactional,自动支持事务处理…...
Vue3路由
文章目录 Vue3路由1. 载入vue-router 库2. 实例2.1 Vue.js vue-router 实现单页应用2.2 router-link创建链接2.3 router-view显示与url对应组件2.4 <router-link> 相关属性 Vue3路由 1. 载入vue-router 库 Vue.js 路由需要载入vue-router 库 安装直接下载地址…...
Android Studio的笔记--aidl实现和调用
android AIDL接口使用 aidl实现新建aidl实现工程build.gradleproguard-rules.pro增加aidl文件 增加aidl实现aidl实现服务打开aidl服务 aidl使用新建aidl使用工程增加aidl文件使用aidl方法 相关回显 aidl实现 新建aidl实现工程 新建一个工程。工程名testaidl。包名com.lxh.tes…...
-[工具包(Toolkit)])
大模型从入门到应用——LangChain:代理(Agents)-[工具包(Toolkit)]
分类目录:《大模型从入门到应用》总目录 工具包是工具的集合,这些工具被设计成一起用于特定的任务,并且具有方便的加载方法。常见的工具包如下: CSV代理JiraJSON代理OpenAPI代理自然语言APIPandas数据框架代理PlayWright浏览器工…...

VR全景算不算好的创业项目?有哪些特性?
现在是全民创业的时代,大家都在找创业项目,那么什么是好的创业项目呢?有人会问VR全景算不算创业好项目呢?一般情况下好的创业项目,发展前景和市场消费群体都是比较大的,市场需求大才能满足多数消费者的需求…...

Spring系列文章:Spring集成Log4j2⽇志框架、整合JUnit
一、集成Log4j2⽇志框架 从Spring5之后,Spring框架⽀持集成的⽇志框架是Log4j2.如何启⽤⽇志框架: 第⼀步:引⼊Log4j2的依赖 <!--log4j2的依赖--> <dependency><groupId>org.apache.logging.log4j</groupId><a…...

flink的网络缓冲区
背景 在flink的taskmanager进行数据交互的过程中,网络缓冲区是一个可以提升网络交换速度的设计,此外,flink还通过网络缓冲区实现其基于信用值credit的流量控制,以便尽可能的处理数据倾斜问题 网络缓冲区 在flink中每个taskmana…...

产品经理学习笔记
产品文档之BRD、MRD和PRD - 知乎BRD、MRD和PRD一起被认为是从市场到产品需要形成的标准规范文档: 1、BRD(Business Requirement Document),商业需求文档,是一份产品商业论证报告,基于商业目标或价值所描述的…...

【深入理解Linux锁机制】七、互斥体
系列文章: 我的圈子:高级工程师聚集地 【深入理解Linux锁机制】一、内核锁的由来 【深入理解Linux锁机制】二、中断屏蔽 【深入理解Linux锁机制】三、原子操作 【深入理解Linux锁机制】四、自旋锁 【深入理解Linux锁机制】五、衍生自旋锁 【深入理解Linux锁机制】六、信…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...
【JavaEE】万字详解HTTP协议
HTTP是什么?-----互联网的“快递小哥” 想象我们正在网上购物:打开淘宝APP,搜索“蓝牙耳机”,点击商品图片,然后下单付款。这一系列操作背后,其实有一个看不见的“快递小哥”在帮我们传递信息,…...

Ansible+Zabbix-agent2快速实现对多主机监控
ansible Ansible 是一款开源的自动化工具,用于配置管理(Configuration Management)、应用部署(Application Deployment)、任务自动化(Task Automation)和编排(Orchestration…...

World-writable config file /etc/mysql/mysql.conf.d/my.cnf is ignored
https://stackoverflow.com/questions/53741107/mysql-in-docker-on-ubuntu-warning-world-writable-config-file-is-ignored 修改权限 -> 重启mysql # 检查字符集配置 SHOW VARIABLES WHERE Variable_name IN (character_set_server, character_set_database ); --------…...
