leetcode分类刷题:二叉树(一、简单的层序遍历)
二叉树的深度优先遍历题目是让我有点晕,先把简单的层序遍历总结下吧:配合队列进行的层序遍历在逻辑思维上自然直观,不容易出错
102. 二叉树的层序遍历
本题是二叉树的层序遍历模板:每次循环将一层节点出队,再将一层节点入队,也是所有可用层序遍历解二叉树题目的模板,只需要在模板里稍加改动即可解题
from typing import List, Optional, Union
from collections import deque
'''
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:输入:root = [3,9,20,null,null,15,7]输出:[[3],[9,20],[15,7]]
题眼:基础
思路:利用队列实现
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、转换为顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)# 2、转换为链式存储:双指针root = tmpTree[0]parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子节点存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1 # 更新遍历双亲节点return rootclass Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if root == None:return []result = []que = deque()que.append(root) # 队列初始值while len(que) > 0:size = len(que) # 当前队列长度==二叉树一层的节点个数layer = []for _ in range(size): # 一层遍历node = que.popleft() # 记录下出队的节点layer.append(node.val)# 和之前深度遍历一样:空节点不入队,不然对None节点取值会出错if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result.append(layer)return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.levelOrder(root))except EOFError:break
107. 二叉树的层序遍历 II
“102. 二叉树的层序遍历”的结果反转/逆序即可
from typing import List, Optional, Union
from collections import deque
'''
107. 二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:输入:root = [3,9,20,null,null,15,7]输出:[[15,7],[9,20],[3]]
题眼:自底向上的层序遍历
思路:“102. 二叉树的层序遍历”的结果反转/逆序即可
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)# 2、链式存储:双指针root = tmpTree[0]parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效if tmpTree[child] != None: # 左孩子有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1return rootclass Solution:def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:# 情况1、树为空if root == None:return []# 情况2、树不为空que = deque()que.append(root)result = []while len(que) > 0:size = len(que) # 当前队列长度==二叉树一层的节点个数layer = []for _ in range(size): # 一层遍历node = que.popleft()layer.append(node.val)if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result.append(layer)# 反转result# left, right = 0, len(result) - 1# while left < right:# result[left], result[right] = result[right], result[left]# left += 1# right -= 1return result[::-1]if __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)print(nums)root = buildBinaryTree(nums)print(obj.levelOrderBottom(root))except EOFError:break
429. N 叉树的层序遍历
一般 层序遍历的基础上,要访问每个节点的N个孩子
from typing import List, Optional, Union
from collections import deque
'''
429. N 叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:输入:root = [1,null,3,2,4,null,5,6]输出:[[1],[3,2,4],[5,6]]
题眼:N 叉树的层序遍历
思路:一般 层序遍历的基础上,要访问每个节点的N个孩子
'''class Node:def __init__(self, val=None, children=None):self.val = valself.children = childrenclass Solution:def levelOrder(self, root: Node) -> List[List[int]]:# 情况1、树为空if root == None:return []# 情况2、树不为空que = deque()que.append(root)result = []while len(que) > 0:size = len(que)layer = []for _ in range(size): # 一层遍历node = que.popleft()layer.append(node.val)if node.children != None:for child in node.children:que.append(child)result.append(layer)return result
637. 二叉树的层平均值
from typing import List, Optional, Union
from collections import deque
'''
637. 二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
示例 1:输入:root = [3,9,20,null,null,15,7]输出:[3.00000,14.50000,11.00000]解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。因此返回 [3, 14.5, 11] 。
题眼:每一层节点的平均值
思路:一般 层序遍历的基础上,计算每一层对应的平均值
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)# 2、转换为链式存储root = tmpTree[0]parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1return rootclass Solution:def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:que = deque()que.append(root)result = []while len(que) > 0:size = len(que) # 当前队列长度==二叉树一层的节点个数s = 0for _ in range(size): # 一层遍历node = que.popleft()s += node.valif node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result.append(s / size)return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.averageOfLevels(root))except EOFError:break
515. 在每个树行中找最大值
from typing import List, Optional, Union
from collections import deque
'''
515. 在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例 1:输入: root = [1,3,2,5,3,null,9]输出: [1,3,9]
题眼:二叉树的层序遍历
思路:一般 层序遍历的基础上,记录每一行的最大值
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、转换为顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)root = tmpTree[0]# 2、转换为链式存储:双指针parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效if tmpTree[child] != None: # 左孩子有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1return rootclass Solution:def largestValues(self, root: Optional[TreeNode]) -> List[int]:# 情况1、树为空if root == None:return []# 情况2、树不为空que = deque()que.append(root)result = []while len(que) > 0:size = len(que) # 当前队列长度==二叉树一层的节点个数n = -float('inf')for _ in range(size): # 一层遍历node = que.popleft()n = max(n, node.val)if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result.append(n)return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.largestValues(root))except EOFError:break
199. 二叉树的右视图
一般 层序遍历的基础上,返回每一层的最后一个元素
from typing import List, Optional, Union
from collections import deque
'''
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:输入:[1,2,3,null,5,null,4]输出:[1,3,4]
题眼:从顶部到底部 从右侧所能看到
思路:一般 层序遍历的基础上,返回每一层的最后一个元素
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、 顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)# 2、链式存储:双指针root = tmpTree[0]parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲结点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子节点存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1return rootclass Solution:def rightSideView(self, root: Optional[TreeNode]) -> List[int]:# 情况1、树为空if root == None:return []# 情况2、树不为空que = deque()que.append(root)result = []while len(que) > 0:size = len(que)for i in range(size): # 一层遍历node = que.popleft()if i == size - 1: # 添加每一层的最后一个元素result.append(node.val)if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.rightSideView(root))except EOFError:break
513. 找树左下角的值
一般 层序遍历的基础上,访问每一层的每个元素时,都把第一个元素进行赋值即可
from typing import List, Optional, Union
from collections import deque
'''
513. 找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:输入: root = [2,1,3]输出: 1
题眼:二叉树的层序遍历
思路:一般 层序遍历的基础上,访问每一层的每个元素时,都把第一个元素进行赋值即可
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)root = tmpTree[0]# 2、链式存储parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲结点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下一个节点的左孩子parent += 1return rootclass Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:que = deque()que.append(root)result = 0while len(que) > 0:size = len(que)for i in range(size):node = que.popleft()if i == 0: # 总是获取层序遍历的每一层第一个值result = node.valif node.left != None:que.append(node.left)if node.right != None:que.append(node.right)return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.findBottomLeftValue(root))except EOFError:break
103. 二叉树的锯齿形层序遍历
一般 层序遍历的基础上,对结果的偶数个逆序一下
from typing import List, Optional, Union
from collections import deque
'''
103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:输入:root = [3,9,20,null,null,15,7]输出:[[3],[20,9],[15,7]]
题眼:基础
思路:一般 层序遍历的基础上,对结果的偶数个逆序一下
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、转换为顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)# 2、转换为链式存储:双指针root = tmpTree[0]parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子节点存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下个节点的左孩子parent += 1 # 更新遍历双亲节点return rootclass Solution:def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:# 情况1、树为空if root == None:return []# 情况2、树不为空que = deque()que.append(root)result = []while len(que) > 0:size = len(que)layer = []for _ in range(size):node = que.popleft()layer.append(node.val)if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result.append(layer)# 对结果的偶数个逆序一下for i in range(1, len(result), 2):result[i] = result[i][::-1]return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.zigzagLevelOrder(root))except EOFError:break
116. 填充每个节点的下一个右侧节点指针
一般 层序遍历的基础上,将每层的节点(除最后一个外)的next值指向下一个节点
from typing import List, Optional, Union
from collections import deque
'''
116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有next 指针都被设置为 NULL。
示例 1:输入:root = [1,2,3,4,5,6,7]输出:[1,#,2,3,#,4,5,6,7,#]解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
题眼:二叉树的层序遍历(满二叉树)
思路:一般 层序遍历的基础上,将每层的节点(除最后一个外)的next值指向下一个节点
'''class Node:def __init__(self, val=0, left=None, right=None, next=None):self.val = valself.left = leftself.right = rightself.next = nextdef buildBinartTree(nums: List[Union[int]]) -> Optional[Node]:if len(nums) == 0:return []if len(nums) == 1:return Node(nums[0])# 1、转换为顺序存储tmpTree = []for n in nums:tmpTree.append(Node(n))root = tmpTree[0]# 2、转换为链式存储parent, child = 0, 1while child < len(tmpTree):tmpTree[parent].left = tmpTree[child] # 满二叉树左孩子一定有效child += 1tmpTree[parent].right = tmpTree[child] # 满二叉树右孩子一定存在且有效child += 1parent += 1return rootclass Solution:def connect(self, root: Optional[Node]) -> Optional[Node]:# 情况1、树为空if root == None:return root# 情况2、树不为空que = deque()que.append(root)while len(que) > 0:size = len(que)pre = Nonefor i in range(size):node = que.popleft()if i == 0: # 记录每层第一个节点为prepre = nodeelse: # 从每层第二个节点开始,都要给pre的next指针赋值pre.next = nodepre = nodeif node.left != None:que.append(node.left)if node.right != None:que.append(node.right)return rootif __name__ == "__main__":while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):nums.append(int(n))print(nums)except EOFError:break
117. 填充每个节点的下一个右侧节点指针 II
一般 层序遍历的基础上,将每层的节点(除最后一个外)的next值指向下一个节点
from typing import List, Union, Optional
from collections import deque
'''
117. 填充每个节点的下一个右侧节点指针 II
给定一个二叉树
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有next 指针都被设置为 NULL。
示例 1:输入:root = [1,2,3,4,5,null,7]输出:[1,#,2,3,#,4,5,7,#]解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
题眼:二叉树的层序遍历(注意不是满二叉树)
思路:一般 层序遍历的基础上,将每层的节点(除最后一个外)的next值指向下一个节点
'''class Node:def __init__(self, val=0, left=None, right=None, next=None):self.val = valself.left = leftself.right = rightself.next = nextdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[Node]:if len(nums) == 0:return Noneif len(nums) == 1:return Node(nums[0])# 1、转换为顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(Node(n))else:tmpTree.append(None)root = tmpTree[0]# 2、转换为链式存储parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲节点有效性判断if tmpTree[child] != None: # 左孩子节点有效性判断tmpTree[parent].left = tmpTree[child]child += 1if child < len(tmpTree) and tmpTree[child] != None: # 左孩子节点存在且有效tmpTree[parent].right = tmpTree[child]child += 1parent += 1return rootclass Solution:def connect(self, root: Optional[Node]) -> Optional[Node]:# 情况1、树为空if root == None:return root# 情况2、树不为空que = deque()que.append(root)while len(que) > 0:size = len(que)pre = Nonefor i in range(size):node = que.popleft()if i == 0: # 记录每层第一个节点为prepre = nodeelse: # 从每层第二个节点开始,都要给pre的next指针赋值pre.next = nodepre = nodeif node.left != None:que.append(node.left)if node.right != None:que.append(node.right)return rootif __name__ == "__main__":while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)print(nums)except EOFError:break
104. 二叉树的最大深度
一般 层序遍历的基础上,输出最大高度值,也就是二叉树的高度值
from typing import List, Optional, Union
from collections import deque
'''
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例 1:输入:[3,9,20,null,null,15,7]输出:3
题眼:二叉树的层序遍历
思路:一般 层序遍历的基础上,输出最大高度值
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)root = tmpTree[0]# 2、链式存储parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲结点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下一个节点的左孩子parent += 1return rootclass Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:# 情况1、树为空if root == None:return 0# 情况2、树不为空result = 0que = deque()que.append(root)while len(que) > 0:size = len(que)for _ in range(size):node = que.popleft()if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result += 1return result# 做完了计算完全二叉树的节点数,用了带return的递归法,有点感觉了,看看能否把这里的迭代法写出来def maxDepthRecursive(self, root: Optional[TreeNode]) -> int:# 1、确定函数参数和返回值def maxDepth(node: Optional[TreeNode]) -> int:# 2、终止条件if node == None:return 0# 3、单次递归的操作leftN = maxDepth(node.left) # 左rightN = maxDepth(node.right) # 右return max(leftN, rightN) + 1 # 中return maxDepth(root)if __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.maxDepth(root))except EOFError:break
111. 二叉树的最小深度
一般 层序遍历的基础上,输出最小高度值(第一次遍历到叶子节点的时候)
from typing import List, Optional, Union
from collections import deque
'''
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:输入:root = [3,9,20,null,null,15,7]输出:2
题眼:二叉树的层序遍历
思路:一般 层序遍历的基础上,输出最小高度值(第一次遍历到叶子节点的时候)
'''class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef buildBinaryTree(nums: List[Union[int, str]]) -> Optional[TreeNode]:if len(nums) == 0:return Noneif len(nums) == 1:return TreeNode(nums[0])# 1、顺序存储tmpTree = []for n in nums:if n != 'null':tmpTree.append(TreeNode(n))else:tmpTree.append(None)root = tmpTree[0]# 2、链式存储parent, child = 0, 1while child < len(tmpTree):if tmpTree[parent] != None: # 双亲结点有效if tmpTree[child] != None: # 左孩子节点有效tmpTree[parent].left = tmpTree[child]child += 1 # 指向右孩子if child < len(tmpTree) and tmpTree[child] != None: # 右孩子存在且有效tmpTree[parent].right = tmpTree[child]child += 1 # 指向下一个节点的左孩子parent += 1return rootclass Solution:def minDepth(self, root: Optional[TreeNode]) -> int:# 情况1、树为空if root == None:return 0# 情况2、树不为空result = 0que = deque()que.append(root)while len(que) > 0:size = len(que)for _ in range(size):node = que.popleft()if node.left == None and node.right == None:return result + 1if node.left != None:que.append(node.left)if node.right != None:que.append(node.right)result += 1return result# 做完了最大深度的递归,试试这个最小深度的,有陷阱!!!def minDepthRecursive(self, root: Optional[TreeNode]) -> int:# 1、确定函数参数和返回值def minD(node: Optional[TreeNode]) -> int:# 2、终止条件if node == None:return 0# 3、单次递归的操作leftN = minD(node.left) # 左rightN = minD(node.right) # 右# 当一个左子树为空,右不为空,这时并不是最低点if node.left == None and node.right != None: # 中return 1 + rightN# 当一个右子树为空,左不为空,这时并不是最低点if node.left != None and node.right == None:return 1 + leftNreturn min(leftN, rightN) + 1return minD(root)if __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')[1].strip()[1: -1]nums = []if in_line != '':for n in in_line.split(','):if n != 'null':nums.append(int(n))else:nums.append(n)root = buildBinaryTree(nums)print(obj.minDepth(root))except EOFError:break
559. N 叉树的最大深度
一般 层序遍历的基础上,遍历children部分
from typing import List, Optional, Union
from collections import deque
'''
559. N 叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。示例 1:输入:root = [1,null,3,2,4,null,5,6]输出:3
题眼:二叉树的层序遍历
思路:一般 层序遍历的基础上,遍历children部分
'''class Node:def __init__(self, val=None, children=None):self.val = valself.children = childrenclass Solution:def maxDepth(self, root: Optional[Node]) -> int:# 情况1、树为空if root == None:return 0# 情况2、树不为空result = 0que = deque()que.append(root)while len(que) > 0:size = len(que)for _ in range(size):node = que.popleft()if node.children != None:for child in node.children:que.append(child)result += 1return result
相关文章:
)
leetcode分类刷题:二叉树(一、简单的层序遍历)
二叉树的深度优先遍历题目是让我有点晕,先把简单的层序遍历总结下吧:配合队列进行的层序遍历在逻辑思维上自然直观,不容易出错 102. 二叉树的层序遍历 本题是二叉树的层序遍历模板:每次循环将一层节点出队,再将一层节点…...

STM32 CAN使用记录:FDCAN基础通讯
文章目录 目的关键配置与代码轮询方式中断方式收发测试 示例链接总结 目的 CAN是非常常用的一种数据总线,被广泛用在各种车辆系统中。这篇文章将对STM32中FDCAN的使用做个示例。 CAN的一些基础介绍与使用可以参考下面文章: 《CAN基础概念》https://blo…...

GB/T 11945-2019 蒸压灰砂实心砖和实心砌块检测
蒸压灰砂砖是以砂、石灰为主要原料,经坯料制备,压制成型、蒸压养护而成的实心砖,简称灰砂砖,具有良好的耐久性能和强度。 GB/T 11945-2019蒸压灰砂实心砖和实心砌块检测: 测试要求 测试标准 抗压强度 GB/T 2542 GB…...
echarts静态饼图
<div class"cake"><div id"cakeChart"></div></div> import * as echarts from "echarts";mounted() {this.$nextTick(() > {this.getCakeEcharts()})},methods: {// 饼状图getCakeEcharts() {let cakeChart echart…...

Linux中的apt与yum
Linux中的apt与yum apt和yum区别 apt和yum执行流程 apt和yum区别 apt 和 yum 是两种不同的包管理工具,用于在 Linux 操作系统中安装、升级和删除软件包。它们主要用于不同的 Linux 发行版。 命令适用系统aptUbuntu、DebianyumCentOS、Redhat 也就是说࿰…...

DQN算法概述及基于Pytorch的DQN迷宫实战代码
一. DQN算法概述 1.1 算法定义 Q-Learing是在一个表格中存储动作对应的奖励值,即状态-价值函数Q(s,a),这种算法存在很大的局限性。在现实中很多情况下,强化学习任务所面临的状态空间是连续的,存在无穷多个状态,这种情…...
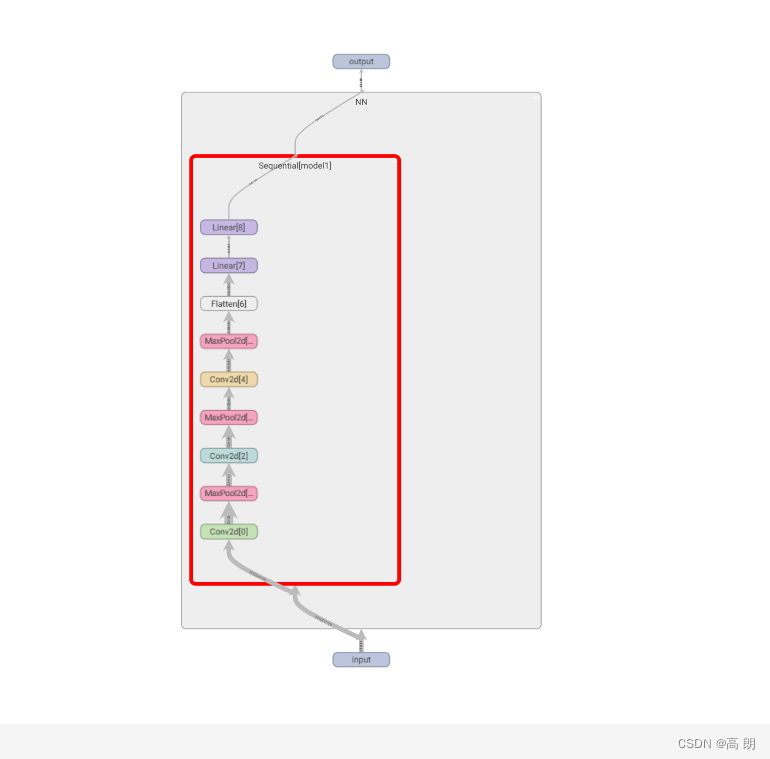
Pytorch学习整理笔记(一)
文章目录 数据处理DatasetTensorboard使用Transformstorchvision数据集使用DataLoader使用nn.Module的使用神经网络 数据处理Dataset 主要是对Dataset的使用: 继承 Dataset实现init方法,主要是进行一些全局变量的定义,在对其初始化时需要赋…...

paddlespeech asr脚本demo
概述 paddlespeech是百度飞桨平台的开源工具包,主要用于语音和音频的分析处理,其中包含多个可选模型,提供语音识别、语音合成、说话人验证、关键词识别、音频分类和语音翻译等功能。 本文介绍利用ps中的asr功能实现批量处理音频文件的demo。…...

算法分析与设计编程题 递归与分治策略
棋盘覆盖 题目描述 解题代码 // para: 棋盘,行偏移,列偏移,特殊行,特殊列 void dividedCovering(vector<vector<int>>& chessBoard, int dr, int dc, int sr, int sc, int size) {if (size 1) return;size / 2…...

Java的XWPFTemplate工具类导出word.docx的使用
依赖 <!-- word导出 --><dependency><groupId>com.deepoove</groupId><artifactId>poi-tl</artifactId><version>1.7.3</version></dependency><!-- 上面需要的依赖--><dependency><groupId>org.ap…...

Science adv | 转录因子SPIC连接胚胎干细胞中的细胞代谢与表观调控
代谢是生化反应网络的结果,这些反应吸收营养物质并对其进行处理,以满足细胞的需求,包括能量产生和生物合成。反应的中间体被用作各种表观基因组修饰酶的底物和辅助因子,因此代谢与表观遗传密切相关。代谢结合表观遗传涉及疾病&…...
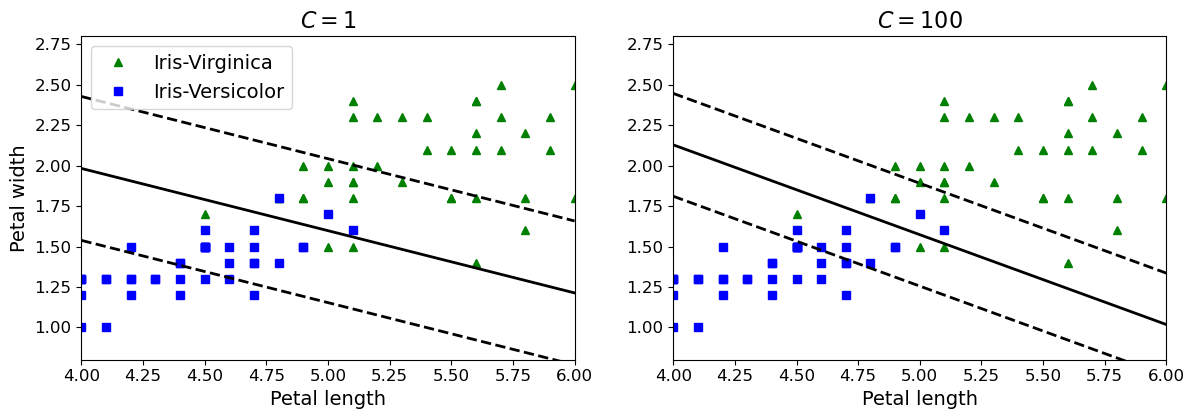
机器学习实战-系列教程7:SVM分类实战2线性SVM(鸢尾花数据集/软间隔/线性SVM/非线性SVM/scikit-learn框架)项目实战、代码解读
🌈🌈🌈机器学习 实战系列 总目录 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 SVM分类实战1之简单SVM分类 SVM分类实战2线性SVM SVM分类实战3非线性SVM 3、不同软间隔C值 3.1 数据标准化的影响 如图左边是没…...

DOM渲染与优化 - CSS、JS、DOM解析和渲染阻塞问题
文章目录 DOM渲染面试题DOM的渲染过程DOM渲染的时机与渲染进程的概述浏览器的渲染流程1. 解析HTML生成DOM树:遇到<img>标签加载图片2. 解析CSS生成CSSOM(CSS Object Model): 遇见背景图片链接不加载3. 将DOM树和CSSOM树合并生成渲染树:加载可视节点…...
基于小程序的理发店预约系统
一、项目背景及简介 现在很多的地方都在使用计算机开发的各种管理系统来提高工作的效率,给人们带来很多的方便。计算机技术从很大的程度上解放了人们的双手,并扩大了人们的活动范围,是人们足不出户就可以通过电脑进行各种事情的管理。信息系…...

MD5 算法流程
先通过下面的命令对 md5算法有个感性的认识: $ md5sum /tmp/1.txt 1dc792fcaf345a07b10248a387cc2718 /tmp/1.txt$ md5sum // 从键盘输入,ctrl-d 结束输入 hello, world! 910c8bc73110b0cd1bc5d2bcae782511 -从上面可以看到,一个文件或一…...

TCP/IP协议详解
TCP/IP(Transmission Control Protocol/Internet Protocol,传输控制协议/互联网协议)是互联网的基本协议,也是国际互联网络的基础。 TCP/IP 不是指一个协议,也不是 TCP 和 IP 这两个协议的合称,而是一个协…...
SSM SpringBoot vue快递柜管理系统
SSM SpringBoot vue快递柜管理系统 系统功能 登录 注册 个人中心 快递员管理 用户信息管理 用户寄件管理 配送信息管理 寄存信息管理 开发环境和技术 开发语言:Java 使用框架: SSM(Spring SpringMVC Mybaits)或SpringBoot 前端: vue 数据库:Mys…...

期权交易保证金比例一般是多少?
期权交易是一种非常受欢迎的投资方式之一,它为期权市场带来了更为多样化和灵活化的交易形式。而其中的期权卖方保证金比例是期权交易中的一个重要指标,直接关系到投资者的风险与收益,下文介绍期权交易保证金比例一般是多少?本文来…...

029:vue项目,勾选后今天不再弹窗提示
第029个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...

Unet语义分割-语义分割与实例分割概述-001
文章目录 前言1、图像分割和图像识别1.语义分割2.实例分割 2、分割任务中的目标函数定义3.IOU 前言 大纲目录 1、图像分割和图像识别 下面是图像识别和图像分割的区别,图像识别就是识别出来,画个框,右边的是图像分割。 1.语义分割 两张图把…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
