【数据结构】二叉树的链式结构
【数据结构】二叉树的链式存储结构
二叉树的存储结构
typedef int BTDataType;
// 二叉树的结构
typedef struct BinaryTreeNode {BTDataType data; // 树的值struct BinaryTreeNode *left; // 左孩子struct BinaryTreeNode *right;// 右孩子
} BinaryTreeNode;
二叉树的深度优先遍历
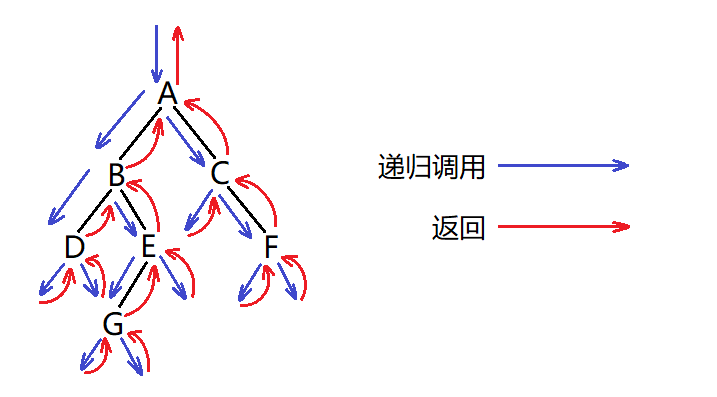
前序遍历
前序遍历,又叫先根遍历。
遍历顺序:根 -> 左子树 -> 右子树
代码:
// 前序遍历
void BinaryTreePrevOrder(BinaryTreeNode *root) {// 前序遍历 根、左子树、右子树// 如果root为空,递归结束if (root == NULL) {printf("NULL ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
中序遍历
中序遍历,又叫中根遍历。
遍历顺序:左子树 -> 根 -> 右子树
代码:
// 中序遍历
void BinaryTreeInOrder(BinaryTreeNode *root) {// 中序遍历 - 左子树、根、右子树if (root == NULL) {printf("NULL ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}
后序遍历
后序遍历,又叫后根遍历。
遍历顺序:左子树 -> 右子树 -> 根
代码:
// 后序遍历
void BinaryPostOrder(BinaryTreeNode *root) {// 后序遍历 - 左子树、右子树、根if (root == NULL) {printf("NULL ");return;}BinaryPostOrder(root->left);BinaryPostOrder(root->right);printf("%d ", root->data);
}
二叉树的广度优先遍历
层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
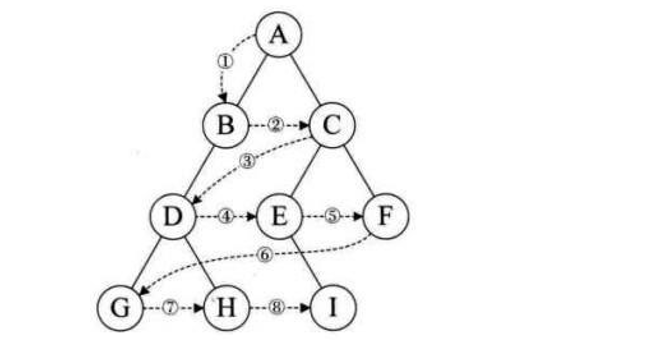
思路(借助一个队列):
- 先把根入队列,然后开始从队头出数据。
- 出队头的数据,把它的左孩子和右孩子依次从队尾入队列(NULL不入队列)。
- 重复进行步骤2,直到队列为空为止。

特点:借助队列先进先出的性质,上一层数据出队列的时候带入下一层数据。
// 层序遍历 - 利用队列
void BinaryTreeLevelOrder(BinaryTreeNode *root) {// 创建一个队列,队列中入数据,取队头,然后带左右子树,出一个数,带一个树的所有子树Queue q;QueueInit(&q);if (root) {// root不为NULL,就入队列QueuePush(&q, root);}while (!QueueEmpty(&q)) {// 取队头,打印BinaryTreeNode *front = QueueFront(&q);printf("%d ", front->data);// 取完POPQueuePop(&q);// 取队头,带下一层,if (front->left) {QueuePush(&q, front->left);}if (front->right) {QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
二叉树的节点个数
求解树的节点总数时,可以将问题拆解成子问题:
- 若为空,则结点个数为0。
- 若不为空,则结点个数 = 左子树节点个数 + 右子树节点个数 + 1(自己)。
代码:
// 求二叉树节点个数
int BinaryTreeSize(BinaryTreeNode *root) {if (root == NULL) {return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
二叉树的叶子节点个数
子问题拆解:
- 若为空,则叶子结点个数为0。
- 若结点的左指针和右指针均为空,则叶子结点个数为1。
- 除上述两种情况外,说明该树存在子树,其叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数。
代码:
// 求二叉树的叶子节点个数
int BinaryTreeLeafSize(BinaryTreeNode *root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
第K层节点的个数
思路:
相对于根结点的第k层结点的个数 = 相对于以其左孩子为根的第k-1层结点的个数 + 相对于以其右孩子为根的第k-1层结点的个数。

代码:
// 求第k层的节点个数 k>=1
int BinaryTreeLevelSize(BinaryTreeNode *root, int k) {if (root == NULL) {return 0;}if (k == 1) {return 1;}return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}
值为x的节点
子问题:
- 先判断根结点是否是目标结点。
- 再去左子树中寻找。
- 最后去右子树中寻找。
代码:
// 二叉树查找值为x的节点
BinaryTreeNode *BinaryTreeFind(BinaryTreeNode *root, BTDataType x) {if (root == NULL) {return NULL;}if (root->data == x) {return root;}// 左子树递归的节点保存到leftTree中,如果leftTree不为NULL,则return leftTreeBinaryTreeNode *leftTree = BinaryTreeFind(root->left, x);if (leftTree) {return leftTree;}// 右子树递归的节点保存到rightTree中,如果rightTree不为NULL,则return rightTreeBinaryTreeNode *rightTree = BinaryTreeFind(root->right, x);if (rightTree) {return rightTree;}// 找不到,返回NULLreturn NULL;
}
树的高度
子问题:
- 若为空,则深度为0。
- 若不为空,则树的最大深度 = 左右子树中深度较大的值 + 1。
代码:
// 求二叉树的高度
int BinaryTreeHeight(BinaryTreeNode *root) {// 求左子树的高度,右子树的高度// 取最大的if (root == NULL) {return 0;}int leftHeight = BinaryTreeHeight(root->left);int rightHeight = BinaryTreeHeight(root->right);//如果左右子树两边相等就取左边的高度,所以大于等于return leftHeight >= rightHeight ? leftHeight + 1 : rightHeight + 1;
}
判断二叉树是否是完全二叉树
判断二叉树是否是完全二叉树的方法与二叉树的层序遍历类似,但又有一些不同。
思路(借助一个队列):
- 先把根入队列,然后开始从队头出数据。
- 出队头的数据,把它的左孩子和右孩子依次从队尾入队列(NULL也入队列)。
- 重复进行步骤2,直到读取到的队头数据为NULL时停止入队列。
- 检查队列中剩余数据,若全为NULL,则是完全二叉树;若其中有一个非空的数据,则不是完全二叉树。
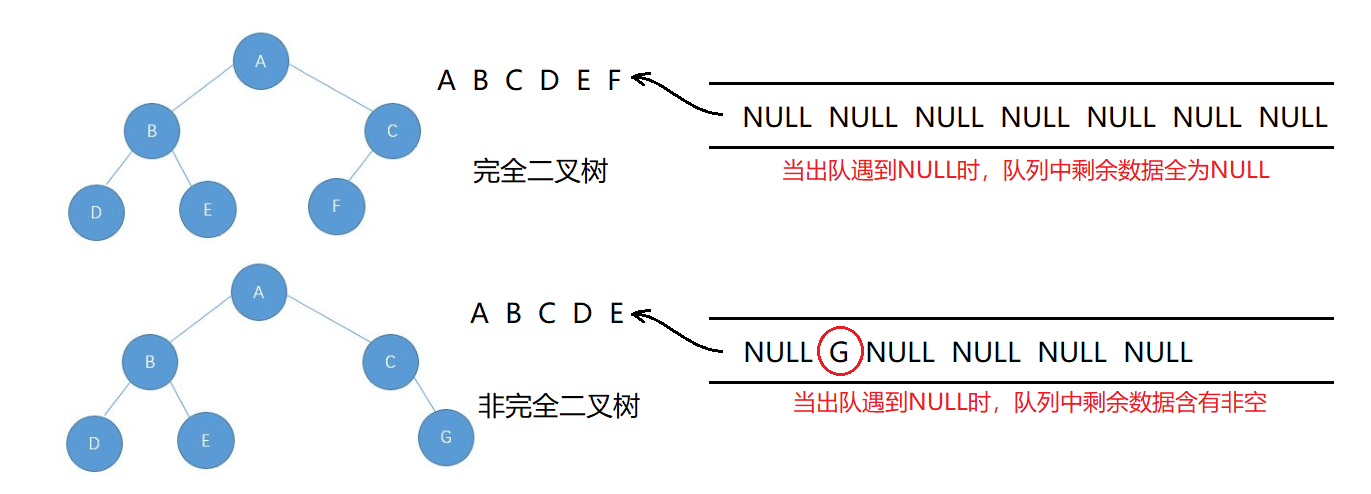
代码:
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BinaryTreeNode *root) {// 层序走,走到第一个为空的时候,就跳出去,如果是满二叉树,后面的节点都应该为空Queue q;QueueInit(&q);if (root) {QueuePush(&q, root);}while (!QueueEmpty(&q)) {BinaryTreeNode *front = QueueFront(&q);QueuePop(&q);if (front == NULL) {break;} else {QueuePush(&q, front->left);QueuePush(&q, front->right);}}// 出到空以后,如果后面全是空,则是完全二叉树while (!QueueEmpty(&q)) {BinaryTreeNode *front = QueueFront(&q);QueuePop(&q);if (front != NULL) {QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
判断二叉树是否是单值二叉树
单值二叉树,所有节点的值都相同的二叉树即为单值二叉树,判断某一棵二叉树是否是单值二叉树的一般步骤如下:
- 判断根的左孩子的值与根结点是否相同。
- 判断根的右孩子的值与根结点是否相同。
- 判断以根的左孩子为根的二叉树是否是单值二叉树。
- 判断以根的右孩子为根的二叉树是否是单值二叉树。
若满足以上情况,则是单值二叉树。
注:空树也是单值二叉树。
代码:
//求单值二叉树
bool isUnivalTree(BinaryTreeNode *root) {if (root == nullptr) {return true;}if (root->left && root->data != root->left->data) {return false;}if (root->right && root->data != root->right->data) {return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}
判断二叉树是否是对称二叉树
对称二叉树,这里所说的对称是指镜像对称:
要判断某二叉树是否是对称二叉树,则判断其根结点的左子树和右子树是否是镜像对称即可。因为是镜像对称,所以左子树的遍历方式和右子树的遍历方式是不同的,准确来说,左子树和右子树的遍历是反方向进行的。
代码:
//求对称二叉树
bool _isSymmetric(BinaryTreeNode *left, BinaryTreeNode *right) {// 两个都为NULL,对称if (left == NULL && right == NULL)return true;// 两个其中一个为NULL,一个不为NULL,不对称if (left == NULL || right == NULL)return false;// left的左孩子的值和right的值不相等,不对称if (left->data != right->data)return false;// 左子树的左孩子,和右子树的右孩子对比,然后左子树的右孩子和右子树的左孩子在对比return _isSymmetric(left->left, right->right) && _isSymmetric(left->right, right->left);
}bool isSymmetric(BinaryTreeNode *root) {if (root == nullptr) {return true;}return _isSymmetric(root->left, root->right);
}
翻转二叉树
思路:
- 翻转左子树。
- 翻转右子树。
- 交换左右子树的位置。
代码:
BinaryTreeNode *invertTree(BinaryTreeNode *root) {if (root == nullptr) {return nullptr;}BinaryTreeNode *leftTree = invertTree(root->left);BinaryTreeNode *rightTree = invertTree(root->right);root->left = rightTree;root->right = leftTree;return root;
}
二叉树的构建和销毁
// 申请树节点
BinaryTreeNode *BuyBinaryTreeNode(BTDataType x) {BinaryTreeNode *newnode = (BinaryTreeNode *) malloc(sizeof(BinaryTreeNode));if (newnode == NULL) {perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BinaryTreeNode *BinaryTreeCreate(BTDataType *a, int *pi) {if (a[*pi] == '#') {(*pi)++;return NULL;}BinaryTreeNode *root = (BinaryTreeNode *) malloc(sizeof(BinaryTreeNode));if (root == NULL) {perror("malloc fail");exit(-1);}root->data = a[(*pi)++];root->left = BinaryTreeCreate(a, pi);root->right = BinaryTreeCreate(a, pi);return root;
}
销毁:
// 二叉树销毁
void BinaryTreeDestory(BinaryTreeNode **root) {if (*root == NULL) {return;}// 后序遍历销毁,根要最后释放BinaryTreeDestory(&(*root)->left);BinaryTreeDestory(&(*root)->right);free(*root);*root = NULL;
}
相关文章:

【数据结构】二叉树的链式结构
【数据结构】二叉树的链式存储结构 二叉树的存储结构 typedef int BTDataType; // 二叉树的结构 typedef struct BinaryTreeNode {BTDataType data; // 树的值struct BinaryTreeNode *left; // 左孩子struct BinaryTreeNode *right;// 右孩子 } BinaryTreeNode;二…...
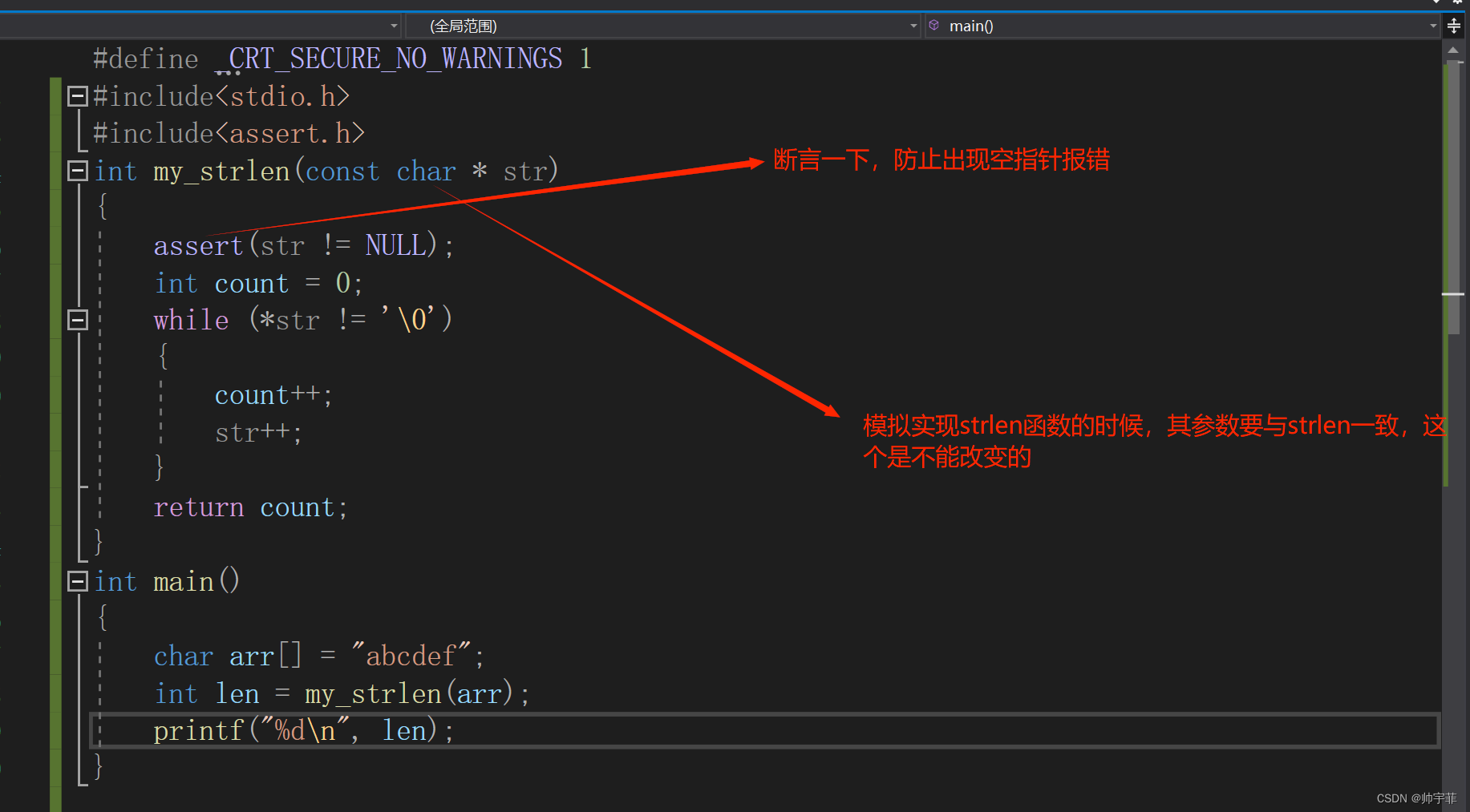
模拟实现C语言--strlen函数
模拟实现C语言–strlen函数 模拟实现C语言--strlen函数一、strlen函数是什么?二、strlen函数的模拟实现2.1 计数器方式实现strlen函数2.2 不创建临时变量计数器方式实现strlen函数2.3 指针-指针方式实现strlen函数 三、strlen函数的返回类型 一、strlen函数是什么&a…...

Spring Boot + Vue的网上商城之物流系统实现
Spring Boot Vue的网上商城之物流系统实现 思路 当构建一个物流系统时,我们可以按照以下步骤进行: 设计数据模型:首先确定系统中需要存储的数据,例如物流公司信息、物流订单信息等。根据需求设计相应的数据模型,包括…...

释放数据价值这道难题,Smartbi V11有解
《未来简史》预言:数据将成为人们未来的信仰。 未来已来,将至已至。如今,数据所扮演的角色与作用超乎想象。从政府将数据要素列入生产要素之中,到数据驱动型业务场景涌现,企业与组织对于数据及其价值的认可度明显提升…...

Day_14 > 指针进阶(3)> bubble函数
目录 1.回顾回调函数 2.写一个bubble_sort函数 2.1认识一下qsort函数 编辑2.2写bubble_sort函数 今天我们继续深入学习指针 1.回顾回调函数 我们回顾一下之前学过的回调函数 回调函数就是一个通过函数指针调用的函数 如果你把函数的指针(地址)…...
sql中怎么查books表下面的内容
要查询 books 表中的所有内容,你可以使用以下 SQL 语句: USE bookmanagement; -- 选择数据库 SELECT * FROM books; -- 查询books表中的所有内容如果你使用的是命令行界面 (mysql 客户端) 来操作数据库,可以直接在命令提示符中输入上述命令…...
Vulnhub系列靶机---HarryPotter-Aragog-1.0.2哈利波特系列靶机-1
文章目录 方式一信息收集主机发现端口扫描目录扫描wpscan工具 漏洞利用msf工具数据库权限用户权限root提权 方式二信息收集gobuster扫描wpscan扫描 漏洞利用POC 靶机文档:HarryPotter: Aragog (1.0.2) 下载地址:Download (Mirror) 方式一 信息收集 主机…...

.NET 8发布首个RC,比.NET 7的超级快更快
.NET 8 发布了首个 RC。据称 RC 阶段会发布两个版本,正式版将于 2023 年 11 月 14 日至 16 日在 .NET Conf 2023 上推出。.NET 8 是长期支持 (LTS) 版本,将会获得 3 年技术支持。 公告写道,此版本为 Android 和 WASM 引入了全新的 AOT 模式、…...
在 Substance Painter中自定义Shader
为什么要学习在Substance Painter中自定义Shader? 答:需要实现引擎与Substance Painter中的渲染效果一致,材质的配置也一致,所见即所得。 基础概述 首先在着色器设置这里,我们可以查看当前渲染使用的着色器 如果没有…...
【自学开发之旅】Flask-restful-Jinjia页面编写template-回顾(五)
restful是web编程里重要的概念 – 一种接口规范也是一种接口设计风格 设计接口: 要考虑:数据返回、接收数据的方式、url、方法 统一风格 rest–表现层状态转移 web–每一类数据–资源 资源通过http的动作来实现状态转移 GET、PUT、POST、DELETE path…...
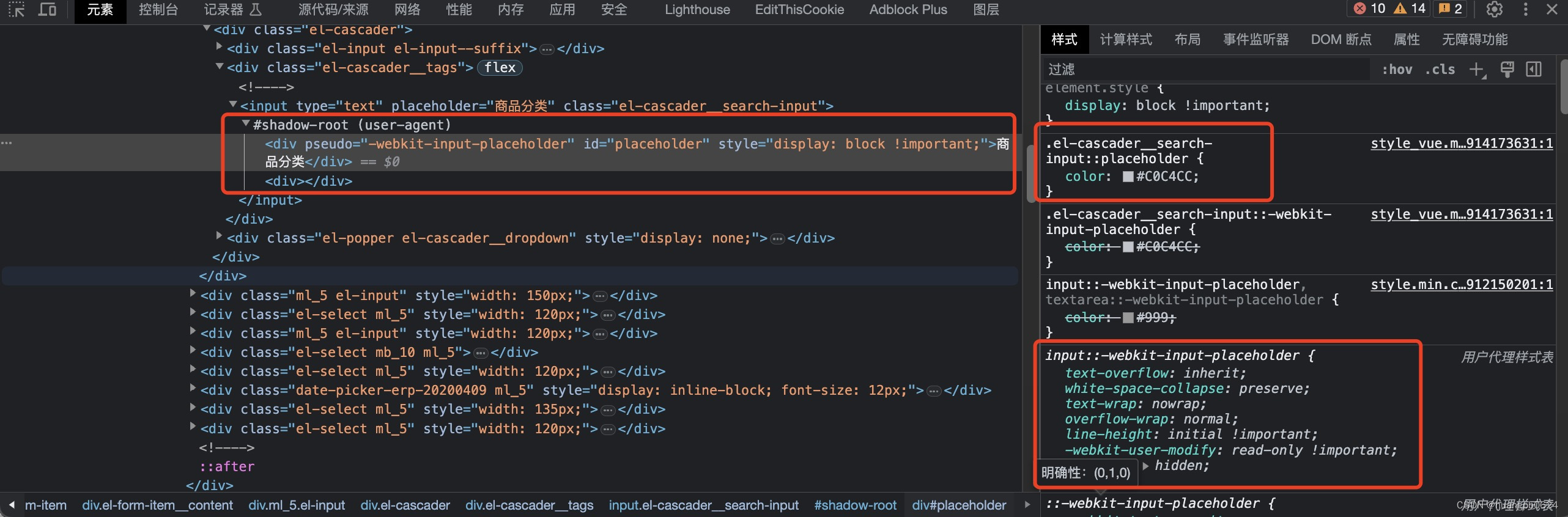
input 的 placeholder 样式
::placeholder 伪元素 这个伪元素可以改变 input、textarea 占位文本的样式。 input::placeholder {color: green; }完整的兼容性写法: input {&::-webkit-input-placeholder, /* WebKit browsers*/ &:-moz-input-placeholder, /* Mozilla Firefox 4 to …...

4.4-Spring源码循环依赖终极讲解
回顾上期内容 new 容器 new AnnotateBeanDefinitionReader 的时候创建很多创世纪的类,其中有一个ConfigurationPostProcessor是用来解析配置类的,将其注册起来存到Bean定义的Map中【这个类是基于Bean工厂后置处理器的】 这一步是将配置类注册到Bean定…...

腾讯云4核8G服务器选CVM还是轻量比较好?价格对比
腾讯云4核8G云服务器可以选择轻量应用服务器或CVM云服务器标准型S5实例,轻量4核8G12M服务器446元一年,CVM S5云服务器935元一年,相对于云服务器CVM,轻量应用服务器性价比更高,轻量服务器CPU和CVM有区别吗?性…...

数学实验-素数(Mathematica实现)
一、实验名称:素数 二、实验环境:Mathematica 10.3软件 三、实验目的:本实验将探讨素数的规律,研究素数的判别、最大的素数、构成生成素数的公式和素数的分布,并学会求解某些范围内的素数。 四、实验内容、步骤以及…...

Vue3样式绑定
文章目录 Vue3样式绑定1. class 属性绑定1.1 v-bind:class 设置一个对象,从而动态的切换 class1.2 在对象中传入更多属性用来动态切换多个 class1.3 直接绑定数据里的一个对象1.4 绑定一个返回对象的计算属性。这是一个常用且强大的模式1. 5 数据语法1.6 errorClass…...
【深度学习】 Python 和 NumPy 系列教程(廿二):Matplotlib详解:2、3d绘图类型(8)3D饼图(3D Pie Chart)
一、前言 Python是一种高级编程语言,由Guido van Rossum于1991年创建。它以简洁、易读的语法而闻名,并且具有强大的功能和广泛的应用领域。Python具有丰富的标准库和第三方库,可以用于开发各种类型的应用程序,包括Web开发、数据分…...
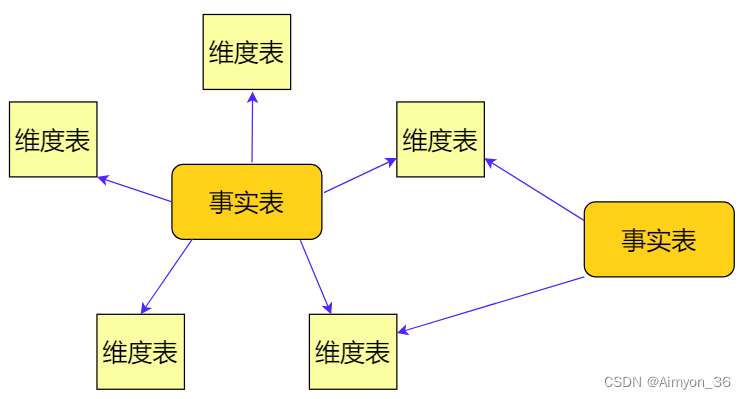
数仓主题域和数据域、雪花模型,星型模型和星座模型
数仓模型和领域划分 一、主题域和数据域的差别二、雪花模型,星座模型和星型模型 一、主题域和数据域的差别 明确数据域作为数仓搭建的重要一环,能够让数仓的数据便于管理和应用。 数据域和主题域都是数据仓库中的重要概念,但含义略有不同&am…...
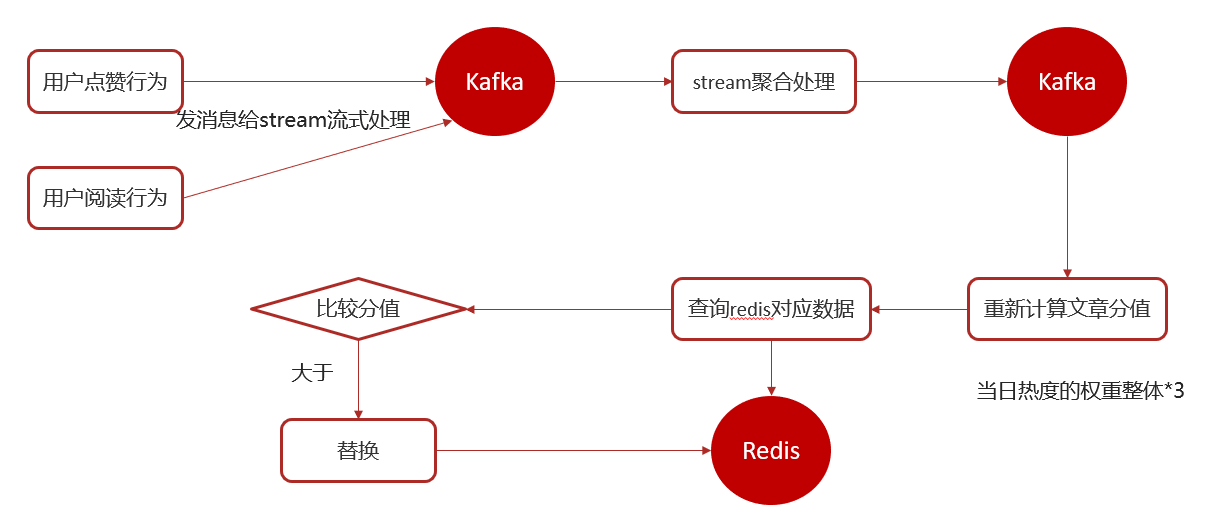
黑马头条 热点文章实时计算、kafkaStream
热点文章-实时计算 1 今日内容 1.1 定时计算与实时计算 1.2 今日内容 kafkaStream 什么是流式计算kafkaStream概述kafkaStream入门案例Springboot集成kafkaStream 实时计算 用户行为发送消息kafkaStream聚合处理消息更新文章行为数量替换热点文章数据 2 实时流式计算 2…...

数据分析:利用gpt进行归因分析
prompt: 你是某电商平台的一名数据分析师,发现昨日的GMV环比下降了5%,请对这数据变动做出归因。 output: 在电商行业中,GMV(总销售额)是一个非常重要的指标,用于衡量业务的整体健康…...
Python工程师Java之路(p)Module和Package
文章目录 1、Python的Module和Package2、Java的Module和Package2.1、Module2.1.1、分模块开发意义2.1.2、模块的调用 2.2、Package Module通常译作模块,Package通常译作包 1、Python的Module和Package Python模块(Module):1个以.…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
