算法leetcode|80. 删除有序数组中的重复项 II(rust重拳出击)
文章目录
- 80. 删除有序数组中的重复项 II:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
80. 删除有序数组中的重复项 II:
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {print(nums[i]);
}
样例 1:
输入:nums = [1,1,1,2,2,3]输出:5, nums = [1,1,2,2,3]解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
样例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]输出:7, nums = [0,0,1,1,2,3,3]解释:函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
提示:
- 1 <= nums.length <= 3 * 104
- -104 <= nums[i] <= 104
- nums 已按升序排列
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 这道题和 26. 删除有序数组中的重复项 非常相似,不同的是,本题允许相同元素最多有一次重复。
- 如果要删除重复,使用映射表等数据结构去计数是比较直观的想法,但是题目要求只能使用常数级别的额外空间,所以不能靠装备只能靠技巧了。
- 题目中有一个非常重要的信息,那就是有序,这意味着相同的数字都会挨在一起,也就是最多允许当前下标和前一个下标的数字相同,判断当前下标和前面的前面的下标数字是否相同即可快速判断重复,即
nums[i]和nums[i - 2]相同时,就要删除该元素。 - 由于要求是原地修改,所以我们需要一个新数组的长度(本身返回值也要求新数组的长度),还需要一个遍历下标,即双指针,只需要遍历一次,并且只需要常数级的额外空间,非常高效。
- 另外如果数组元素少于3个(或者说数组长度小于/等于2个),是肯定满足题意的,可以直接返回,不需要做任何处理。
题解:
rust:
impl Solution {pub fn remove_duplicates(nums: &mut Vec<i32>) -> i32 {let n = nums.len();if n <= 2 {return n as i32;}let (mut slow, mut fast) = (2, 2);while fast < n {if nums[slow - 2] != nums[fast] {nums[slow] = nums[fast];slow += 1;}fast += 1;}return slow as i32;}
}
go:
func removeDuplicates(nums []int) int {n := len(nums)if n <= 2 {return n}slow, fast := 2, 2for fast < n {if nums[slow-2] != nums[fast] {nums[slow] = nums[fast]slow++}fast++}return slow
}
c++:
class Solution {
public:int removeDuplicates(vector<int>& nums) {const int n = nums.size();if (n <= 2) {return n;}int slow = 2, fast = 2;while (fast < n) {if (nums[slow - 2] != nums[fast]) {nums[slow] = nums[fast];++slow;}++fast;}return slow;}
};
python:
class Solution:def removeDuplicates(self, nums: List[int]) -> int:slow = 2for fast in range(2, len(nums)):if nums[fast] != nums[slow - 2]:nums[slow] = nums[fast]slow += 1return slowjava:
class Solution {public int removeDuplicates(int[] nums) {final int n = nums.length;if (n <= 2) {return n;}int slow = 2, fast = 2;while (fast < n) {if (nums[slow - 2] != nums[fast]) {nums[slow] = nums[fast];++slow;}++fast;}return slow;}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:
)
算法leetcode|80. 删除有序数组中的重复项 II(rust重拳出击)
文章目录 80. 删除有序数组中的重复项 II:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 80. 删除有序数组中的重复项 II: …...

Vite 完整版详解
1. 打包构建: Vite 使用 Rollup 作为默认的构建工具。通过运行 npm run build 命令,Vite 会将应用程序的源代码打包成一个或多个优化的静态文件,以便在生产环境中进行部署。Vite 的构建过程会根据需要进行代码拆分、压缩和优化,以…...

AI入门指南:探索人工智能的基础原理和实际应用
引言 介绍AI的基本概念:什么是人工智能,为什么它如此重要。 引出博客的主要内容,即AI的基础原理和实际应用。 第一部分:AI的基础原理 什么是人工智能: 解释AI的定义和范畴。 介绍AI的历史和发展。 机器学习入门&#x…...
使用 Webpack 从 0 到 1 构建 Vue3 项目 + ts
使用 Webpack 从 0 到 1 构建 Vue3 项目 1.初始化项目结构2.安装 webpack,补充智能提示3.初步编写 webpack.config.js3.1设置入口文件及出口文件3.2 指定 html 模板位置 4.配置 运行/打包 命令,首次打包项目5.添加 Vue 及相关配置5.1安装并引入 vue5.2 补…...

【Git】Git 分支
Git 分支 1.分支简介 为了真正理解 Git 处理分支的方式,我们需要回顾一下 Git 是如何保存数据的。 或许你还记得 起步 的内容, Git 保存的不是文件的变化或者差异,而是一系列不同时刻的 快照 。 在进行提交操作时,Git 会保存一…...
.NET Upgrade Assistant 升级 .NET MAUI
.NET Upgrade Assistant 是一种可帮助您将应用程序升级到最新的 .NET版本 的工具,并且您可以使用这个工具将您的应用程序从旧平台(例如 Xamarin Forms 和 UWP)迁移到新的平台。此外,这个新版本的工具,可以让您在不更改…...
记一次诡异的Cannot find declaration to go to,Cannot resolve method
记一次诡异的 Cannot find declaration to go to, Cannot resolve method getOnExpressions in Join 对于项目中通常问题,清除缓存,重启idea,或者仔细检查语法通常都能解决问题,但是这次却失效了,以下是原…...
智慧园区:AI边缘计算技术与视频监控汇聚平台打造智慧园区解决方案
一、行业趋势与背景 智慧园区是现代城市发展的重要组成部分,通过智能化技术提高园区的运营效率、降低成本、增强环境可持续性等具有重要作用。在智慧园区中,人工智能和视频汇聚技术是重要的前置技术。人工智能技术可以实现对数据的智能化处理和分析&…...

SpringCloud(17~21章):Alibaba入门简介、Nacos服务注册和配置中心、Sentinel实现熔断与限流、Seata处理分布式事务
17 SpringCloud Alibaba入门简介 17.1 why会出现SpringCloud alibaba Spring Cloud Netflix项目进入维护模式 https://spring.io/blog/2018/12/12/spring-cloud-greenwich-rc1-available-now 说明 Spring Cloud Netflix Projects Entering Maintenance Mode 什么是维护模…...
Jmeter安装与测试
目录 一:JMeter简介: 二:JMeter安装与配置 三:JMeter主要原件 一:JMeter简介: JMeter,一个100%的纯Java桌面应用,由Apache组织的开放源代码项目,它是功能 …...

java开发环境从0开始 【汇总版】
java开发环境从零开始 第一步:jdk第二步:安装 mysql第三步:安装maven第四步:idea最新免费安装第五步:安装navicate第六步 :安装git, 第一步:jdk 第一步当然是最先安装java开发环境啦。 看这个链…...
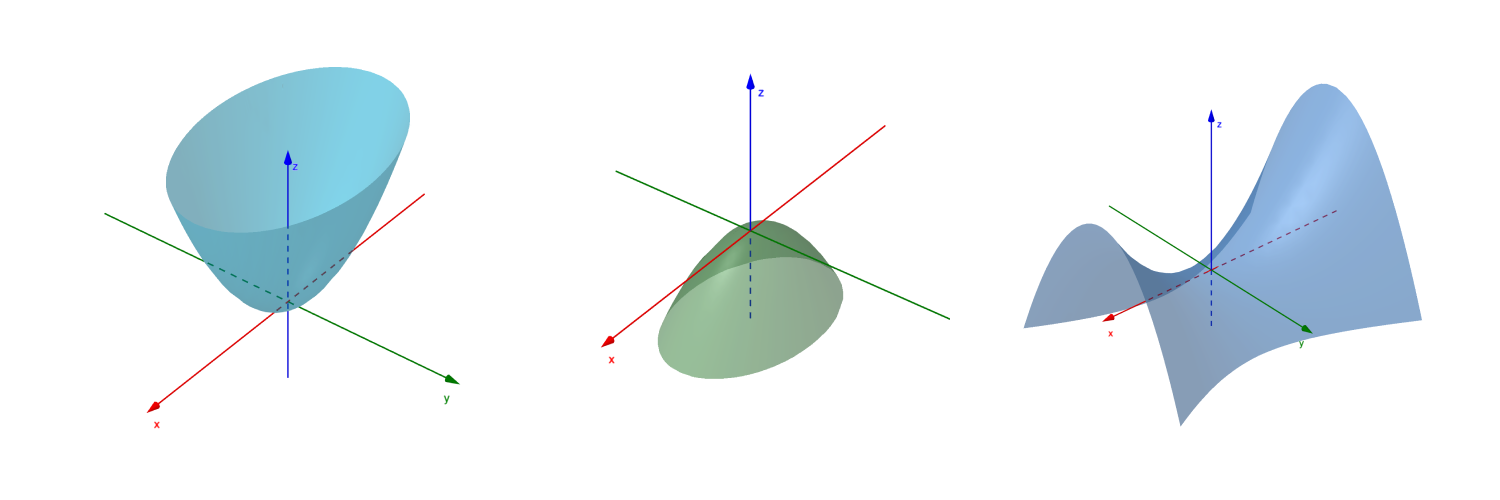
线性代数的本质(九)——二次型与合同
文章目录 二次型与合同二次型与标准型二次型的分类度量矩阵与合同 二次型与合同 二次型与标准型 Grant:二次型研究的是二次曲面在不同基下的坐标变换 由解析几何的知识,我们了解到二次函数的一次项和常数项只是对函数图像进行平移,并不会改变…...
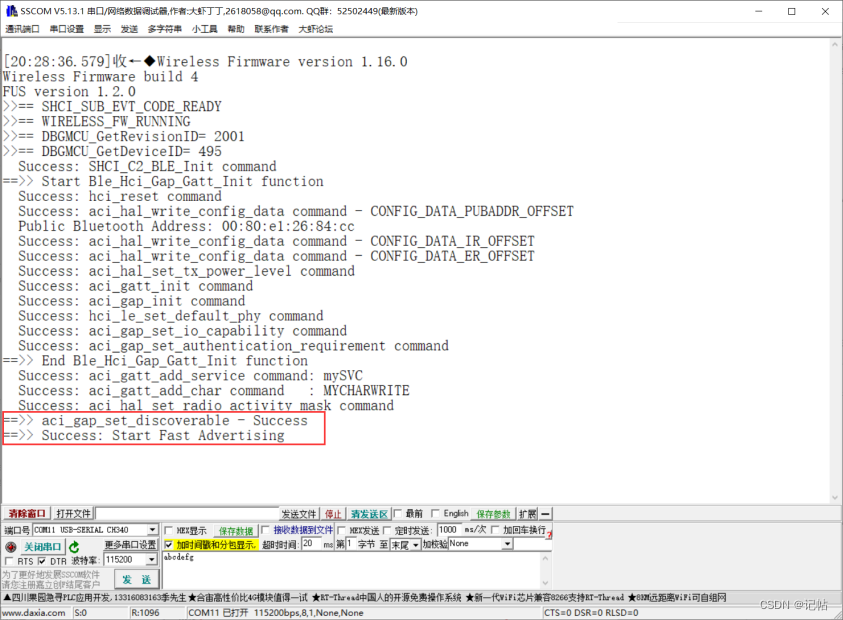
STM32WB55开发(4)----配置串口打印Debug调试信息
STM32WB55开发----4.配置串口打印Debug调试信息 概述硬件准备视频教学样品申请选择芯片型号配置时钟源配置时钟树RTC时钟配置查看开启STM32_WPAN条件配置HSEM配置IPCC配置RTC启动RF开启蓝牙开启串口调试配置蓝牙参数设置工程信息工程文件设置Keil工程配置代码配置结果演示 概述…...

云原生服务无状态(Stateless)特性的实现
文章目录 为何要使用无状态服务?无状态服务的实现方法1. 会话状态外部化2. 负载均衡3. 自动伸缩4. 容器编排5. 数据存储6. 安全性 示例:使用Spring Boot实现无状态服务结论 🎉欢迎来到云计算技术应用专栏~云原生服务无状态(Statel…...
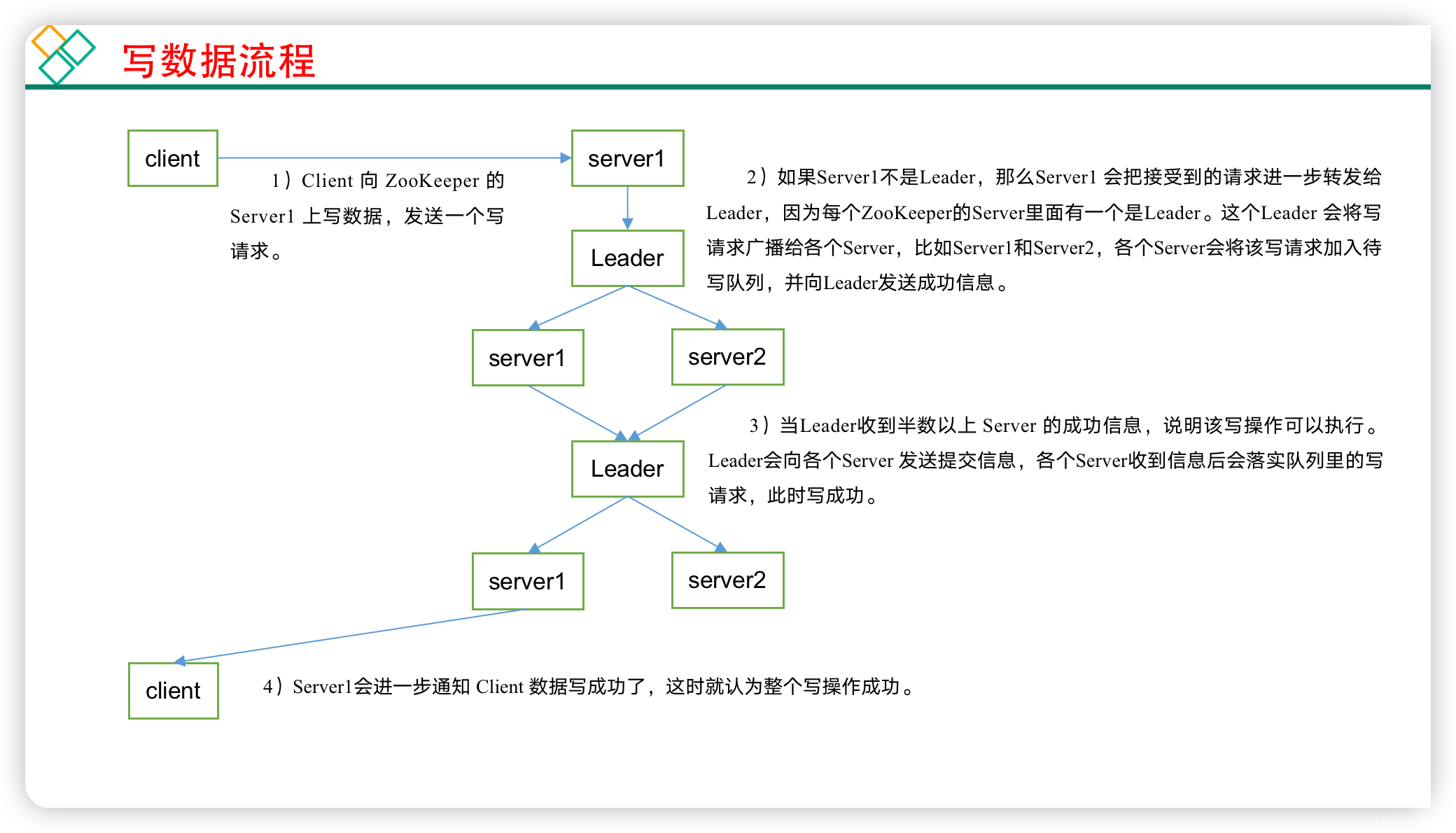
zookeeper最基础教程
文章目录 一、简介1、工作机制2、特点3、数据结构4、应用场景5、选举机制 二、软件安装1、单机版安装2、集群安装3、配置参数解读(zoo.cfg)4、ZK集群启动脚本 三、命令行操作1、语法2、使用3、节点相关4、监听器原理5、节点删除与查看 三、写数据流程 一、简介 1、工作机制 官…...

又一重磅利好来袭!Zebec Payroll 集成至 Nautilus Chain 主网
流支付协议 Zebec Protocol 正在积极的拓展自身生态,随着此前其全新路线图的发布,揭示了该生态从 Web3 世界向 Web2 世界跨越的决心。根据其最新路线图,Zebec Protocol 正在从最初构建在 Solana 上的流支付协议,拓展为囊括模块化公…...

NLP模型的tokenize方法中return_tensors参数
NLP模型的tokenize方法中return_tensors参数 在许多NLP模型的tokenize方法中,return_tensors参数可以指定tokenize之后返回的张量类型,常见的可选值包括: ‘tf’: 返回TensorFlow的张量对象Tensor。 ‘pt’: 返回PyTorch的张量对象torch.Tensor。 ‘np’: 返回NumPy的ndarray对…...
模方新建工程时,显示空三与模型坐标系不一致怎么解决
答:检查空三xml与模型的metadata.xml的坐标系是否一致,metadata文件是否有在data目录外面。 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.0新增单体化建模模块,…...

氧化锌避雷器绝缘电阻测试
氧化锌避雷器 绝缘电阻测试 试验目的 避雷器绝缘电阻包括本体绝缘电阻和底座绝缘电阻, 主要目的在于初步检查避雷 器内部是否受潮; 有并联电阻者可检查其通、 断、 接触和老化等情况。 试验设备 高压绝缘电阻测试仪 厂家: 湖北众拓高试 试验方法 本体绝缘电阻试验…...

链动2+1系统开发
什么是链动21模式? 链动21主要是一个集团队搭设、快速提升产品销量,与消费者做到合作共赢的一个商业模式,让用户在享受购物折扣的同时,也能获得相对收益,同时公司也能达到产品快速销售这样的一个目的,而链…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
