DFS寻找从s到t的所有路径
问题描述:
输入一个有向图,输出从s到t的所有路径的结点
输入:
3 3
0 1
1 2
0 2
输出:
0 1 2
0 2
代码:
#include<bits/stdc++.h>
using namespace std;const int N = 103;
vector<int>e[N];//用行为N的,列为可变长度的二维数组表示邻接表
bool vis[N];//定义访问标记数组
int path[N],cnt;//path用于记录路径,cnt用于记录路径长度(cnt初值为0,全局变量默认为0)
int n,m;//n为结点数,m为边数 void dfs(int s,int t){//找到从s到t的所有路径vis[s] = 1;//第一件事永远都是把当前结点置为已访问path[cnt++] = s;//把当前结点加入路径中 if(s==t){//如果找到一条从s到t的路径for(int i=0;i<cnt;++i){printf("%d ",path[i]);//打印路径}printf("\n");vis[s] = 0;//回溯操作,如果不回溯,则结果只能找到一条从s到t的路径 cnt--;//回溯 return;}for(int i=0;i<e[s].size();++i){//如果当前还没找到s到t路径,继续访问当前s的下一个邻接点 e.[s].size表示,当前结点s的邻接点的个数 if(!vis[e[s][i]]){//如果第s行,第i个结点没有被访问过,则继续访问 dfs(e[s][i],t);//继续从当前扫描到的结点出发去寻找到t的路径 }}vis[s]=0;//回溯,如果没有找到路径,也要回溯,因为如果访问过s之后,就无法再访问当前这个s结点了,也只会找到一条路径 cnt--;
}int main(void){while(~scanf("%d%d",&n,&m)&&(n||m)){//输入结点数n和边数m for(int i=0;i<n;++i){e[i].clear();//把邻接表中每一行的节点数清空,相当于初始化邻接表 } for(int i=0;i<m;++i){//输入边 int x,y;scanf("%d%d",&x,&y);e[x].push_back(y);//如果是有向图,只需要在x后面连上y即可 // e[y].push_back(x);如果是无向图,同样也要在y结点后面加上x } dfs(0,n-1);}return 0;
}相关文章:

DFS寻找从s到t的所有路径
问题描述: 输入一个有向图,输出从s到t的所有路径的结点 输入: 3 3 0 1 1 2 0 2输出: 0 1 2 0 2 代码: #include<bits/stdc.h> using namespace std;const int N 103; vector<int>e[N];//用行为N的…...
分享!JetBrains IDE中的GitLab支持
GitLab是流行的基于git的软件开发和部署平台之一,虽然很长一段时间以来,所有基本git操作都已经可以通过GitLab实现,但GitLab集成仍是JetBrains社区的一大最热门请求。为此,JetBrains团队今年与GitLab联手提供了这种类型的集成。 …...
jq弹窗拖动改变宽高
预览效果 <div classtishiMask><div class"tishiEm"><div id"coor"></div><div class"topNew ismove"><span class"ismove">提示</span><p onclick"closeTishi()"></p&…...

时间不确定度在分布式系统中的说明
On the one hand 时间不确定度问题和影响在分布式系统中 说明 时钟不确定度(Clock Uncertainty)是指在分布式系统中,由于网络延迟、时钟漂移等因素导致系统中各个节点时钟的不同步现象。这种不同步可能会影响到分布式系统的一致性和正确性…...

VMware vCenter 从6.7跨版本升级至7.0U3N
本文尝试使用 vCenter Server Appliance 管理界面 (VAMI) 进行对vCenter Server Appliance7应用进行小版本升级,从6.7.0.47000升级到7.0.3.01600(7.0U3N)。 一、升级前的准备工作 1、检查当前运行环境(当前为6.7.0.47000&#x…...
大麦订单生成器最新版 大麦订单一键生成截图
1.可以一键添加,生成的假订单没有水印,界面也很真实。 2.在软件中输入生成的信息,这是产品信息,选择生成的产品图像,最后生成它。 后台一键生成,独立后台管理 教程:解压源码,修改数…...

如何对Map集合的key进行大小写转换?
工具类: ToUpperCaseKeyMapUtil.java public class ToUpperCaseKeyMapUtil {//对单一的mappublic static <T> Map<String, T> toUpperCaseKeyMap(Map<String, T> map) {if (map ! null) {List<String> mapKeyList new ArrayList<>…...

将函数实现放到CPP报“无法解析的外部符号...”,系VS Bug
发现一个现象,就是项目中有一个类,如果将函数实现全部放到头文件中,编译不报错,如果将函数实现放到CPP中则始终提示“无法解析的外部符号...”,考虑到放到头文件中能正常编译运行,显然这里不符合“无法解析…...
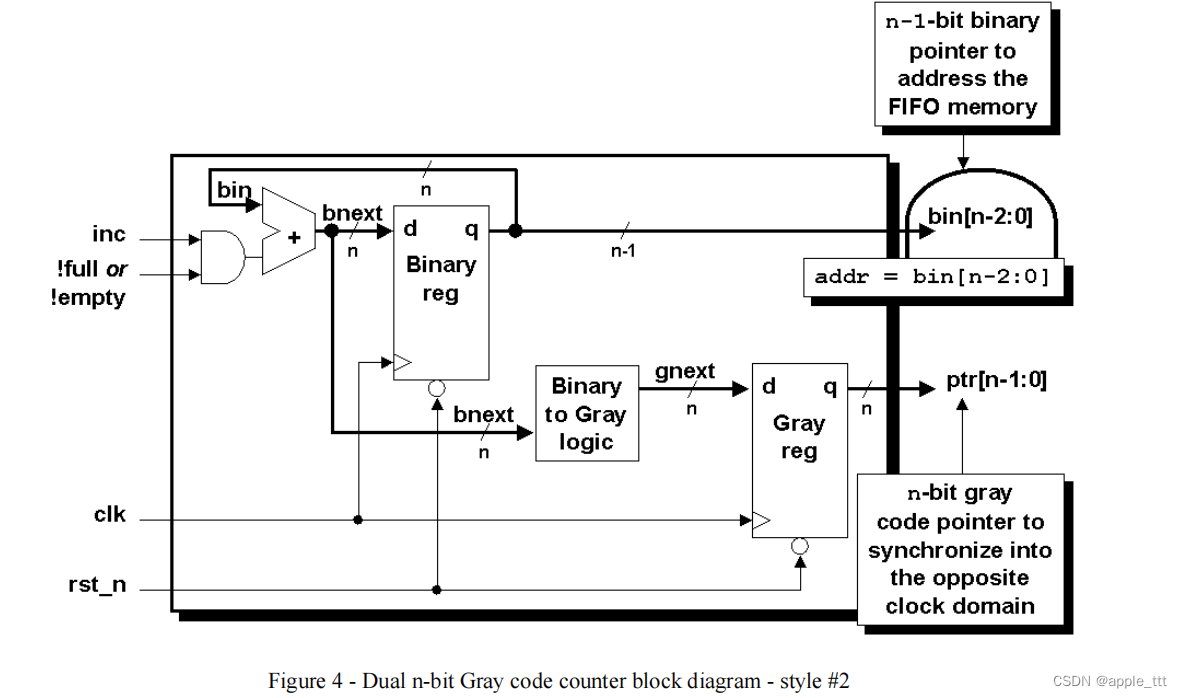
异步FIFO设计的仿真与综合技术(3)
概述 本文主体翻译自C. E. Cummings and S. Design, “Simulation and Synthesis Techniques for Asynchronous FIFO Design 一文,添加了笔者的个人理解与注释,文中蓝色部分为笔者注或意译。前文链接: 异步FIFO设计的仿真与综合技术…...

什么是区块链,解释区块链的原理和应用场景
1、什么是区块链,解释区块链的原理和应用场景。 区块链是一种分布式数据库,它由一系列按照时间顺序排列的数据块组成,并采用密码学方式保证不可篡改和不可伪造。区块链技术最初起源于比特币,作为比特币的底层技术,用于…...

使用bert进行文本二分类
构建BERT(Bidirectional Encoder Representations from Transformers)的训练网络可以使用PyTorch来实现。下面是一个简单的示例代码: import torch import torch.nn as nn from transformers import BertModel, BertTokenizer# Load BERT to…...

用Windows Installer CleanUp Utility 在windows server上面将软件卸载干净,比如SQLSERVER
这里写自定义目录标题 下载文件:Windows Installer CleanUp Utility。 通过以上工具可以将一个应用程序卸载干净。...

Java手写LinkedList和拓展
Java手写LinkedList和拓展 思维导图 #mermaid-svg-K0RTlFFvnikDRvqp {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-K0RTlFFvnikDRvqp .error-icon{fill:#552222;}#mermaid-svg-K0RTlFFvnikDRvqp .error-text{fill…...
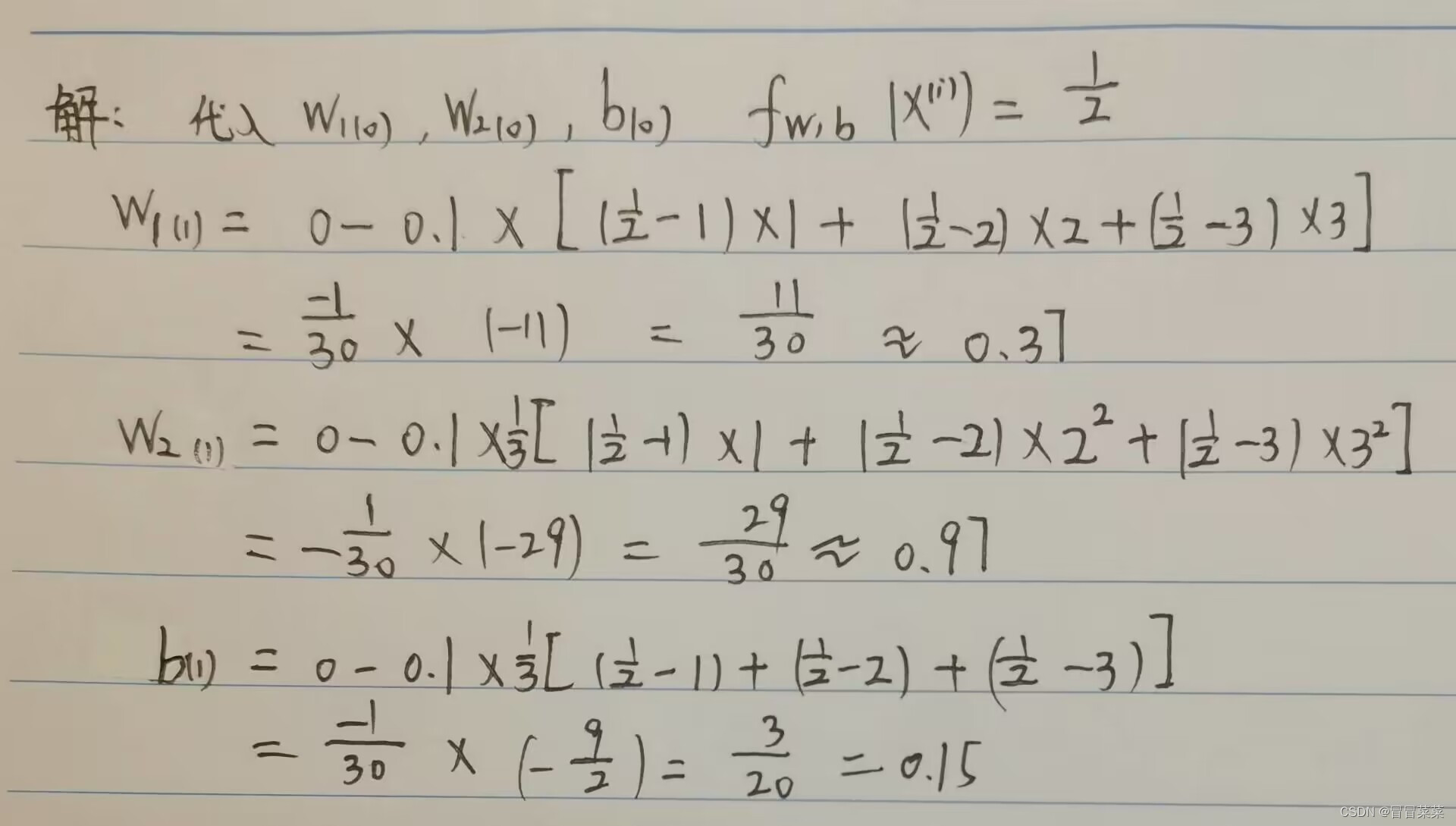
机器学习(14)---逻辑回归(含手写公式、推导过程和手写例题)
逻辑回归 一、逻辑回归概述二、模型、策略和优化(手写)三、w和b的梯度下降公式推导四、例题分析4.1 题目4.2 解答 一、逻辑回归概述 1. 逻辑回归也称作logistic回归分析,是一种广义的线性回归分析模型,属于机器学习中的监督学习。…...
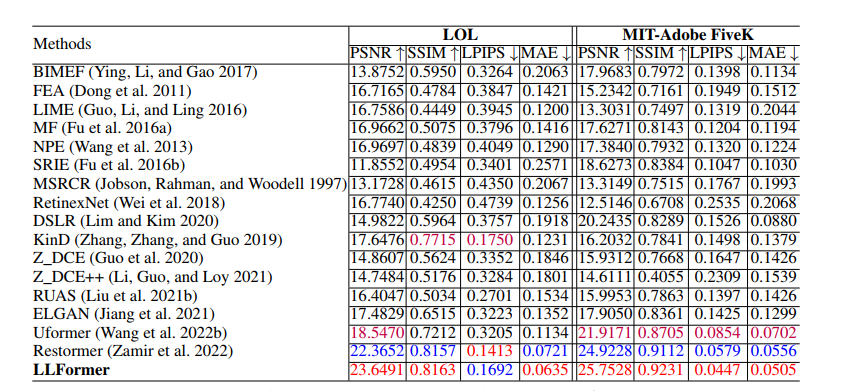
LLFormer 论文阅读笔记
Ultra-High-Definition Low-Light Image Enhancement: A Benchmark and Transformer-Based Method 这是南京大学在AAAI 2023发表的一篇AAAI2023 超高清图像暗图增强的工作。提出了一个超高清暗图增强数据集,提供了4K和8K的图片,同时提出了一个可用于暗图…...

JSP语法基础习题
目录 简答题:jsp中静态include和动态include的区别是什么? 简答题:jsp有哪些内置对象,作用分别是什么? 简答题:Request对象的主要方法有哪些? 代码题: 简答题:jsp中静态…...

vue类与样式的绑定列表渲染
目录 1.类与样式的绑定 1.1绑定 HTML class 1.2绑定数组 1.3绑定内联样式 绑定数组 2.列表渲染 2.1v-for 2.2v-for 与对象 2.3在 v-for 里使用范围值 1.类与样式的绑定 1.1绑定 HTML class 我们可以给 :class (v-bind:class 的缩写) 传递一个对象来动态切换 class…...

vue3+element-plus权限控制实现(el-tree父子级不关联情况处理)
文章目录 前言一、遇到的交互场景el-tree 中 check-strictly 属性 二、处理父级的半选中以及选中交互el-treecheck,check-change 事件编辑进来,父级的半选状态处理 总结 前言 在开发后台管理系统的时候,用户的权限控制是一个常见的需求。这里…...

js中事件委托和事件绑定之间的区别
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 事件绑定(Event Binding)⭐事件委托(Event Delegation)⭐ 选择事件绑定或事件委托⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本…...

Android 11.0 系统system模块开启禁用adb push和adb pull传输文件功能
1.使用场景 在进行11.0的系统定制化开发中,在一些产品中由于一些开发的功能比较重要,防止技术点外泄在出货产品中,禁用 adb pull 和adb push等命令 来获取系统system下的jar 和apk 等文件,所以需要禁用这些命令 2.系统system模块开启禁用adb push和adb pull传输文件功能的…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
