【洛谷 P1364】医院设置 题解(图论+深度优先搜索)
医院设置
题目描述
设有一棵二叉树,如图:
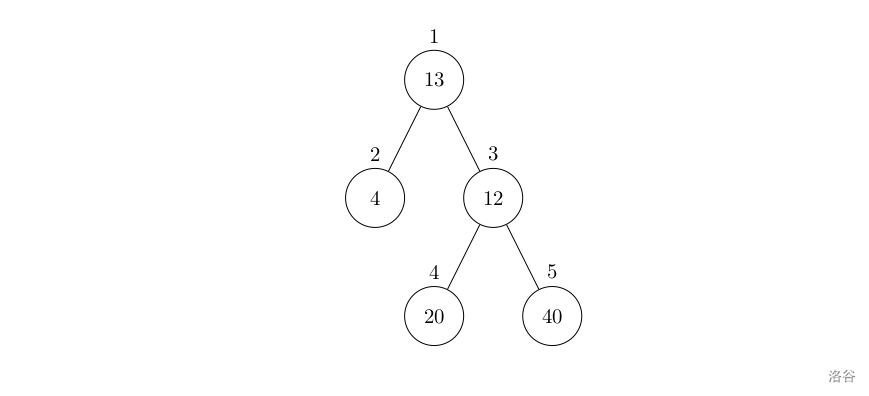
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 1 1 1。如上图中,若医院建在 1 1 1 处,则距离和 = 4 + 12 + 2 × 20 + 2 × 40 = 136 =4+12+2\times20+2\times40=136 =4+12+2×20+2×40=136;若医院建在 3 3 3 处,则距离和 = 4 × 2 + 13 + 20 + 40 = 81 =4\times2+13+20+40=81 =4×2+13+20+40=81。
输入格式
第一行一个整数 n n n,表示树的结点数。
接下来的 n n n 行每行描述了一个结点的状况,包含三个整数 w , u , v w, u, v w,u,v,其中 w w w 为居民人口数, u u u 为左链接(为 0 0 0 表示无链接), v v v 为右链接(为 0 0 0 表示无链接)。
输出格式
一个整数,表示最小距离和。
样例 #1
样例输入 #1
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
样例输出 #1
81
提示
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 1 ≤ n ≤ 100 1 \leq n \leq 100 1≤n≤100, 0 ≤ u , v ≤ n 0 \leq u, v \leq n 0≤u,v≤n, 1 ≤ w ≤ 1 0 5 1 \leq w \leq 10^5 1≤w≤105。
思路
将二叉树储存为一张图,存图时要存双向边。
暴力枚举每个节点作为医院,然后分别计算所有节点到这个医院的距离的加权和。
使用 DFS 遍历整张图,对于当前遍历的节点 x x x,用一个变量 s u m sum sum 记录所有已经遍历的节点到当前节点 x x x 的距离的加权和,用一个 bitset 变量 v i s vis vis 记录所有已经遍历过的节点,然后递归地遍历 x x x 的所有邻接节点,计算它们到 x x x 的距离的加权和,并将其加到 s u m sum sum 上。
为了避免重复遍历已经遍历过的节点,并方便计算节点到达医院的距离,需要在遍历之前将 v i s [ x ] vis[x] vis[x] 设为 1 1 1,在遍历之后再将其设为 0 0 0。
遍历完所有的节点后,用一个变量 a n s ans ans 记录所有节点作为医院时的最小距离和,然后每次更新 a n s = min ( a n s , s u m ) ans=\min(ans,sum) ans=min(ans,sum)。最后输出 a n s ans ans 即可。
AC代码
#include <iostream>
#include <bitset>
#include <algorithm>
#include <cstring>
#define AUTHOR "HEX9CF"
using namespace std;const int N = 1005;// 链式前向星
struct Sedge
{int to;int next;
} edge[N];
int head[N];
int cnt = 0;
int w[N];int n;
int tmp;
int sum;
int ans;bitset<N> vis;void add(int u, int v)
{if (u && v){edge[cnt].to = v;edge[cnt].next = head[u];head[u] = cnt++;}
}void dfs(int x)
{if (vis[x]){return;}sum += w[x] * vis.count();// cout << x << endl;vis[x] = 1;for (int i = head[x]; ~i; i = edge[i].next){dfs(edge[i].to);}vis[x] = 0;
}int main()
{memset(head, -1, sizeof(head));cin >> n;for (int i = 1; i <= n; i++){int a, b;cin >> w[i] >> a >> b;add(i, a);add(i, b);add(a, i);add(b, i);}for (int i = 1; i <= n; i++){sum = 0;vis.reset();dfs(i);if (1 == i){ans = sum;}else{ans = min(ans, sum);}// cout << sum << endl;}cout << ans << endl;return 0;
}相关文章:

【洛谷 P1364】医院设置 题解(图论+深度优先搜索)
医院设置 题目描述 设有一棵二叉树,如图: 其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接…...

【Java基础】- RMI原理和使用详解
【Java基础】- RMI原理和使用详解 文章目录 【Java基础】- RMI原理和使用详解一、什么RMI二、RMI原理2.1 工作原理图2.2 工作原理 三、RMI远程调用步骤3.1 RMI远程调用运行流程图3.2 RMI 远程调用步骤 四、JAVA RMI简单实现4.1 如何实现一个RMI程序4.2 JAVA实现RMI程序 一、什么…...

无水印免费4K视频素材网站 可商用-Free Stock Video
Free Stock Video是一个在线无水印免费4K视频素材网站,提供各种类型的4k、1080p的视频素材共免费下载,包括美食、水、自然、冬季、无人机、云朵、慢动作、夕阳、动态背景、缩时摄影、旅游和烟火,也可通过关键词搜索方式找到相关视频素材内容&…...

kubesphere中间件部署
微服务部署前中间件部署 一、MySQL部署 1.1 使用Docker实现MySQL主从复制 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql/master/log:/var/log/mysql \ -v /mydata/mysql/master/data:/var/lib/mysql \ -v /mydata/mysql/master/conf:/etc/mysql \ -e My…...

使用 AWS S3 SDK 访问 COS-腾讯云国际站代充
腾讯云国际站对象存储(Cloud Object Storage,COS)提供了 AWS S3 兼容的 API,因此当用户的数据从 S3 迁移到 COS 之后,只需要进行简单的配置修改,即可让客户端应用轻松兼容 COS 服务。下面unirech小编主要介…...

c语言每日一练(15)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。 五道选择题: 1、程序运行的结果…...
如何利用软文推广进行SEO优化(打造优质软文,提升网站排名)
在当今的互联网时代,SEO优化成为了网站推广的关键。而软文推广作为一种有效的推广方式,其优点不仅仅局限于SEO,还可以带来更多的曝光和用户流量。本文将深入探讨如何做好软文推广,从而提升网站排名和流量。 了解目标受众群体 内容…...
)
Java线程池ExecutorService和Executors应用(Spring Boot微服务)
记录:476 场景:在Spring Boot微服务中使用ExecutorService管理Java线程池。使用Executors创建线程池。使用Runnable接口实现类提交线程任务到线程池执行。 版本:JDK 1.8,Spring Boot 2.6.3。 1.线程和线程池基础 JDK自带线程和线程池包位…...

机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[中] 引言回顾:最速下降算法的缺陷经典牛顿法基本介绍经典牛顿法的问题经典牛顿法的优点与缺陷经典牛顿法示例 修正牛顿法介绍拟牛顿法拟牛顿法的算法过程 矩阵 B k 1 \mathcal B_{k1} Bk1的…...

Django系列:Django简介与MTV架构体系概述
Django系列 Django简介与MTV架构体系概述 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/132890054 【介…...

锐捷交换机WEB管理系统EXCU_SHELL密码信息泄漏漏洞
一、漏洞简介 锐捷交换机 WEB 管理系统 EXCU_SHELL存在密码信息泄露漏洞,攻击者可从漏洞获取到管理员账号密码,从而以管理员权限登录。 二、影响版本 锐捷交换机 WEB 管理系统 三、资产测绘 hunterweb.body"img/free_login_ge.gif"&&…...

线性代数(六) 线性变换
前言 《线性空间》定义了空间,这章节来研究空间与空间的关联性 函数 函数是一个规则或映射,将一个集合中的每个元素(称为自变量)映射到另一个集合中的唯一元素(称为因变量)。 一般函数从 “A” 的每个元…...

Python基础运算分享
Python的运算符和其他语言类似 (我们暂时只了解这些运算符的基本用法,方便我们展开后面的内容,高级应用暂时不介绍) 数学运算 >>>print 19 # 加法>>>print 1.3-4 # 减法>>>print 3*5 …...
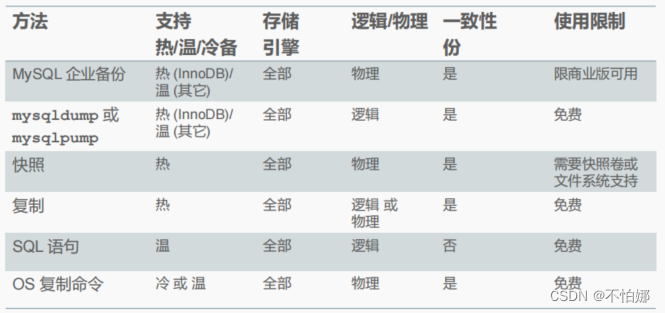
【MySQL】mysql中有哪几种类型的备份技术?它们各自有什么优缺点?
为什么要备份?备份类型(从类型的角度)备份技术(从技术手段的角度)不同备份方法的比较感谢 💖 为什么要备份? 数据库或它所在的平台可能会出现问题,这时候数据库中的数据可能就遭到了…...

5基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。
基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。程序已调通,可以直接运行。 5pytorch多目标粒子群算法最优解5pytorch多目标粒子群算法最优解 (xiaohongshu.co…...

002 Linux 权限
前言 本文将会向您介绍关于linux权限方面的内容,包括文件类型,如何切换用户、基本权限、粘滞位等等 Linux具体的用户 超级用户:可以再linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的…...

【Java 基础篇】Java可变参数:灵活处理不定数量的方法参数
在Java编程中,可变参数是一项强大的功能,它允许你编写更加灵活的方法,接受不定数量的参数。本文将详细解释Java可变参数的用法、语法以及最佳实践。 什么是可变参数? 可变参数是Java 5引入的一项功能,它允许你在方法…...

“网站建设流程详解:从概念到上线的每个细节“
以下是网站建设流程的详细步骤,从概念到上线的每个细节: 确定网站目标和定位:明确网站的主题和目标,根据目标受众和市场定位来决定网站的内容和设计风格。考虑网站的目的、目标受众、行业或领域等方面,以及网站的定位…...

DC/DC开关电源学习笔记(七)低压大电流DC/DC变换技术
低压大电流DC/DC变换技术 1. 无暂态要求的低压大电流DC/DC变换技术2. 负载极其快速变化的低压大电流DC/DC变换技术2.1 非隔离型 VRM2.2 隔离型VRM低压大电流高功率 DC/DC 变换技术,已从前些年的 3.3V 降至现在的 1.0V 左右,电流目前已可达到几十安至几百安。同时,电源的输出指标…...

XUbuntu22.04之查找进程号pidof、pgrep总结(一百九十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
