【数据结构】—堆排序以及TOP-K问题究极详解(含C语言实现)

食用指南:本文在有C基础的情况下食用更佳
🔥这就不得不推荐此专栏了:C语言
♈️今日夜电波:ルミネセンス—今泉愛夏
1:01 ━━━━━━️💟──────── 5:05
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
☸️一、前置知识:两种调整方法
向上调整方法
向下调整方法
✡️二、堆排序
堆排序的思想
记住一个公式!(非常重要!!!)
代码实现
🔯三、TOP-K问题
什么是TOP-K问题?
基本思路
🌰
☸️一、前置知识:两种调整方法
向上调整方法
堆的向上调整方法将新插入的节点从下往上逐层比较,如果当前节点比其父节点大(或小,根据是大根堆还是小根堆),则交换这两个节点。一直向上比较,直到不需要交换为止。这样可以保证堆的性质不变。
具体步骤如下:
1.将新插入的节点插入到堆的最后一位。
2.获取该节点的父节点的位置,比较该节点与其父节点的大小关系。
.如果该节点比其父节点大(或小,根据是大根堆还是小根堆),则交换这两个节点。
4.重复步骤2-3,直到不需要交换为止,堆的向上调整完成。
堆的向上调整的时间复杂度为O(logn),其中n为堆的大小。
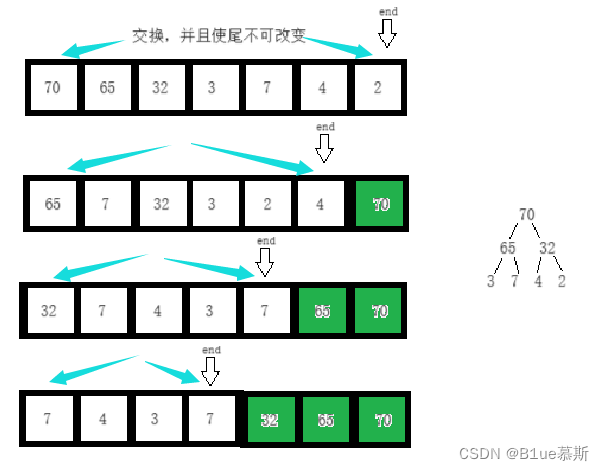
一图让你了解~(以大堆为例)

实现如下:
void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustup(HPDataType* a, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent])//建大堆,小堆则<{swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}向下调整方法
堆的向下调整方法是指将某个节点的值下放至其子节点中,以维护堆的性质的过程。
假设当前节点为 i,其左子节点为 2i+1,右子节点为 2i+2,堆的大小为 n
则向下调整的步骤如下:
-
从当前节点 i 开始,将其与其左右子节点中较小或较大的节点比较,找出其中最小或最大的节点 j。
-
如果节点 i 小于等于(或大于等于,取决于是最小堆还是最大堆)节点 j,则说明它已经满足堆的性质,调整结束;否则,将节点 i 与节点 j 交换位置,并将当前节点 i 更新为 j。
-
重复执行步骤 1 和步骤 2,直到节点 i 没有子节点或已经满足堆的性质。
一图让你了解~(以大堆为例)

实现如下:
void swap(HPDataType* s1, HPDataType* s2)
{HPDataType temp = *s1;*s1 = *s2;*s2 = temp;
}void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个,此为大堆,如果要实现小堆则 改 >{++child;}if (a[child] > a[parent])//此为大堆,如果要实现小堆则 改 >{swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}✡️二、堆排序
堆排序的思想
将待排序的序列构建成一个大根堆或小根堆,然后将堆顶元素与堆底元素交换,再重构堆,重复操作直到有序。堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。算是一种较为高效的排序方法。
具体的实现步骤如下:
-
构建最大堆或最小堆。(建大堆排升序,建小堆排降序)
-
将堆顶元素(最大或最小值)与堆底元素交换。
-
从堆顶开始逐级向下调整堆,保证每个节点都符合堆的性质。
-
重复步骤2和步骤3,直到整个序列有序。
通常而言我们用的都是向下调整法来建堆以及排序,为什么呢?
向下调整法具有较好的时间复杂度:与向上调整法相比,向下调整法的时间复杂度更低,因为向下调整法只需要考虑每个非叶子节点的子树是否满足堆性质,而向上调整法需要考虑每个节点到根节点是否满足堆性质,时间复杂度较高。
记住一个公式!(非常重要!!!)
这个公式是用来干什么的呢?用来找第一个有叶子节点的父节点的!
一图让你了解~

你可能有一个疑惑,我们这样建堆的意义是什么?答案是我们要将所有节点的左子树以及右子树都建成一个我们需要的堆(建大堆排升序,建小堆排降序)。这样做的意义是:让堆顶的元素在同最后一个堆的元素进行调换位置后,能够仅仅通过一次向下调整,(以大堆为例)就能让堆的最大元素排到队尾,并且不打乱顺序!!!
在理解了怎么建堆后,对于排序这件事实际上已经很简单了!
一图让你了解~
代码实现
void HeapSort(int* a, int n)//整体时间复杂度为nlog(n)
{//建大堆排升序,建小堆排降序//用的都是向下调整法来建堆以及排序//这里演示升序,如果要降序则修改向下调整法中的 > 变为 < ,使得建立的为小堆,并且后面的排序也将为降序!//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--)//注意这里的i表示为第一个有叶子结点的父节点{Adjustdown(a, n, i);}//排序int end = n - 1;while (end > 0){swap(&a[0], &a[end]);Adjustdown(a, end, 0);--end;}}🔯三、TOP-K问题
什么是TOP-K问题?
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决。
基本思路
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K 个最小或者最大的元素。
🌰
在随机的10000000个数据中找出前5大的数据。(通过文件建立以及读取实现)
该🌰的堆实现在这篇博文中:堆详解(点我跳转!!!)
实现如下:
void PrintTopK(const char* filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}// 前k个数建小堆for (int i = (k-2)/2; i >=0 ; --i){AdjustDown(minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){// 替换你进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}// fprintf fscanfvoid CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}int main()
{//CreateNDate();PrintTopK("data.txt", 5);return 0;
}感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

【数据结构】—堆排序以及TOP-K问题究极详解(含C语言实现)
食用指南:本文在有C基础的情况下食用更佳 🔥这就不得不推荐此专栏了:C语言 ♈️今日夜电波:ルミネセンス—今泉愛夏 1:01 ━━━━━━️💟──────── 5:05 …...

Python语言概述
视频版教程 Python3零基础7天入门实战视频教程 Python作为一门非常流行的高级编程语言,自从22年开始,TIOBE编程语言排行榜Python一直排第一。 Python简洁高效,丰富的应用场景,受到广大程序员,科研工作者的喜爱。 …...

电子电路学习笔记之NCV84120DR2G——车规级单通道高压侧驱动器
关于车规级芯片: 关于车规级芯片(Automotive Grade Chip),车规级芯片是专门用于汽车行业的芯片,具有高可靠性、高稳定性和低功耗等特点,以满足汽车电子系统的严格要求。这些芯片通常用于车载电子控制单元&…...
YOLO DNF辅助教程完结
课程完结!撒花、撒花、撒花 课程完结!撒花、撒花、撒花 课程完结!撒花、撒花、撒花 呕心沥血三个月,《利用人工智能做DNF游戏辅助》系列实战课程已完结,技术路线贯穿串口通信、目标检测、opencv特征匹配等前沿技术…...

Hadoop-Hive
1. hive安装部署 2. hive基础 3. hive高级查询 4. Hive函数及性能优化 1.hive安装部署 解压tar -xvf ./apache-hive-3.1.2-bin.tar.gz -C /opt/soft/ 改名mv apache-hive-3.1.2-bin/ hive312 配置环境变量:vim /etc/profile #hive export HIVE_HOME/opt/soft/hive…...
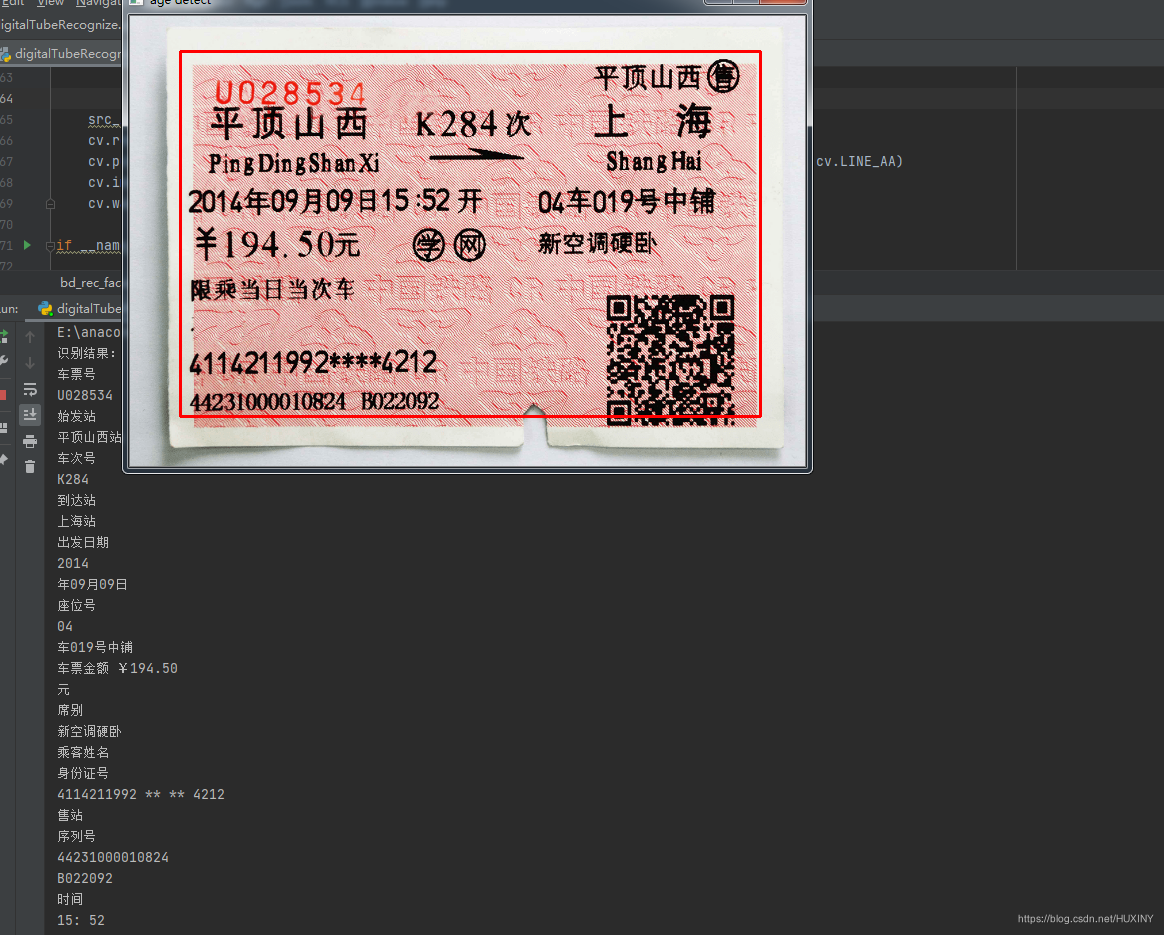
竞赛 基于机器视觉的火车票识别系统
文章目录 0 前言1 课题意义课题难点: 2 实现方法2.1 图像预处理2.2 字符分割2.3 字符识别部分实现代码 3 实现效果最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于机器视觉的火车票识别系统 该项目较为新颖,适合作为竞赛…...

conda与pip镜像源环境配置
文章目录 一. 参考二. conda三. pip 一. 参考 b站环境配置视频 校园网镜像站 二. conda 利用校园网镜像站, 找到conda的镜像源配置文档. 将下面的文档复制到电脑上的.condarc文件中. channels:- defaults show_channel_urls: true default_channels:- https://mirrors.tuna…...

Golang1.21更新内容全面介绍~
我的掘金平台原文地址Golang1.21更新内容全面介绍~ 前言 在Golang1.21这一次更新中,主要更新内容为: for range的一个语义变更 、 新加入max、min、clear方法、 contenxt增添api、 WASI的支持 本文主要带大家熟悉这些变更的内容~ 1.for语义的变更…...
ArcGIS 10.4安装教程!
软件介绍:ArcGIS是一款专业的电子地图信息编辑和开发软件,提供一种快速并且使用简单的方式浏览地理信息,无论是2D还是3D的信息。软件内置多种编辑工具,可以轻松的完成地图生产全过程,为地图分析和处理提供了新的解决方…...
华为云云服务器云耀L实例评测 | 从零开始:华为云云服务器L实例使用教程
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

ElasticSearch配置
2) 搭建ElasticSearch环境 2.1) 拉取镜像 docker pull elasticsearch:7.4.02.2) 创建容器 docker run -id --name elasticsearch -d --restartalways -p 9200:9200 -p 9300:9300 -v /usr/share/elasticsearch/plugins:/usr/share/elasticsearch/plugins -e "discovery.…...

MySQL优化第二篇
MySQL优化第二篇 性能分析小表驱动大表慢查询日志日志分析工具mysqldumpslow Show Profile进行SQL分析(重中之重) 七种JOIN 1、inner join :可以简写为join,表示的是交集,也就是两张表的共同数据 sql语句:…...

基于python解决鸡兔同笼问题
一、什么是鸡兔同笼问题? 鸡兔同笼问题是一个经典的数学问题。问题描述:鸡和兔子共有头数a和脚数b,求鸡和兔子的数量。 解析:设鸡的数量为x,兔子的数量为y,那么可以得到以下两个方程: 1. x y…...

2023 Google 开发者大会|Mobile开发专题追踪
文章目录 前言大会介绍涉及内容MobileWebAICloud Mobile开发专题多终端应用的开发适配大屏视频流可穿戴设备电视新的设计中心 构建高质量的应用高级相机和媒体功能用户的安全和隐私更精细的视觉体验 小结 前言 哈喽大家好,我是阿Q。近期,【2023 Google …...

最新版WPS 2023 加载Zotero方法
安装wps2019vba.exe,获取链接:链接:https://pan.baidu.com/s/1eeoc6Tmwyzxh3n1MFQTVeA 提取码:6431 –来自百度网盘超级会员V8的分享 打开WPS的工具的加载项 添加文件路径,我的在: C:\Users\Administrat…...

详解爬虫策略,反爬虫策略,反反爬爬虫策略
爬虫策略 爬取策略是网络爬虫在执行网页抓取任务时所遵循的规则或策略。这些策略决定了爬虫如何从一个页面转到另一个页面,什么时间进行抓取,以及应该抓取哪些内容。以下是几种常见的爬取策略: 深度优先搜索(DFS) 在…...

ES6中的Promise对象
1. Promise是什么 Promise简单来说就是一个容器,里面保存着未来才会结束的事件的结果(这个事件就是异步操作)。Promise是一个对象(构造函数),可以获取异步操作的结果。 特点: 对象的状态不受外…...

vue 知识点———— 生命周期
1.什么是生命周期 Vue实例从创建到销毁的过程,叫生命周期。 从开始创建、初始化数据、编译模版、挂载Dom-渲染、更新-渲染、销毁等过程。 2.生命周期一共有几个阶段 创建前/后, 载入前/后,更新前/后,销毁前/销毁后 3.初始化相关属性 beforeCreate(创建前…...
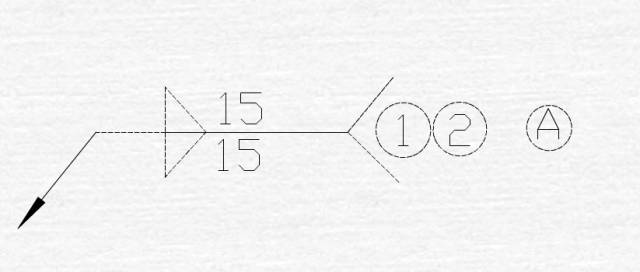
焊接符号学习
欧美焊接符号举例 4.5------表示焊点直径 【3】------根据图示说明,表示此项为CC项或者SC项 6-------表示此处为第六CC项或者SC项 BETWEEN①AND②------表示①件和②件俩点之间的焊点 12X------表示俩点之间的焊点个数为12个 日本焊接符号举例 A------根据图示&…...

记录linux清理空间的步骤
sudo du -sh /* 看整体空间占用情况 [roothost ~]# sudo du -sh /* 0 /bin 143M /boot 85M /data 0 /dev 38M /etc 4.0K /home 0 /lib 0 /lib64 16K /lostfound 4.0K /media 4.0K /mnt 31M /opt 0 /proc 260K /r…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
