python经典百题之水仙花数
题目:打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数
本身。例如:153是一个“水仙花数”,因为153=1的三次方+5的三次方+3的三次方。
方法一:暴力穷举法
思路:先从100开始,依次枚举每个三位数,然后求该数的各位数字的立方和,判断该数是否等于这个立方和。
优点:思路简单,易于理解和实现。
缺点:时间复杂度较高,需要枚举所有的三位数,因此效率较低。
代码实现如下:
for num in range(100, 1000):temp = numsum = 0while temp:digit = temp % 10sum += digit ** 3temp //= 10if sum == num:print(num)
方法二:优化穷举法
思路:可以在穷举的过程中加入一些剪枝操作,例如可以只对各位数字和为指定值的数进行计算,这样可以减少不必要的计算。
优点:在一定程度上提高了效率。
缺点:仍然需要枚举所有的三位数。
代码实现如下:
for i in range(1, 10):for j in range(0, 10):for k in range(0, 10):num = i * 100 + j * 10 + kif num == i ** 3 + j ** 3 + k ** 3:print(num)
方法三:数学公式法
思路:根据水仙花数的定义,可以得到一个三位数的各位数字立方和的公式,即 num = i3 + j3 + k**3。根据这个公式,可以迅速判断一个数是否是水仙花数。
优点:不需要枚举所有的三位数,直接根据公式进行判断,效率较高。
缺点:思维难度较大,难以想到该公式。
代码实现如下:
for num in range(100, 1000):i = num // 100j = num // 10 % 10k = num % 10if num == i**3 + j**3 + k**3:print(num)
综上所述,数学公式法是最优解,但需要对数学公式有一定的理解和掌握。暴力穷举法虽然简单易懂,但效率较低,优化穷举法则在一定程度上提高了效率,但仍需要枚举所有的三位数。
相关文章:

python经典百题之水仙花数
题目:打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数 本身。例如:153是一个“水仙花数”,因为1531的三次方+5的三次方+3的三次方。 方法一:暴…...

jvm的调优工具
1. jps 查看进程信息 2. jstack 查看进程的线程 59560为进程id 产生了死锁就可以jstack查看了 详细用途可以看用途 3. jmap 如何使用dump文件看下 查看 4.jstat 空间占用和次数 5. jconsole可视化工具 各种使用情况,以及死锁检测 6. visualvm可视化工具…...
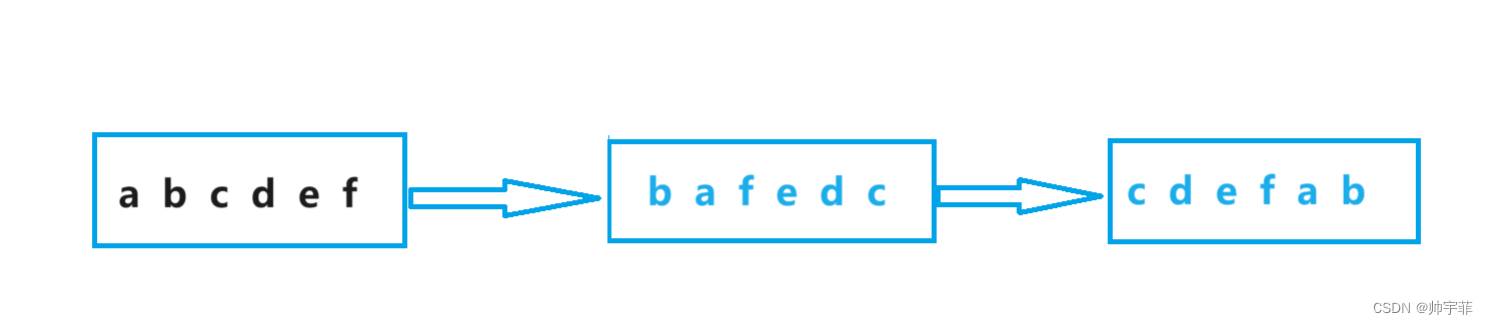
C语言--字符串旋转笔试题
C语言–字符串旋转笔试题 文章目录 C语言--字符串旋转笔试题一、字符串左旋1.1 思路11.2 思路1代码1.3 思路21.4 思路2代码 二、字符串旋转结果判断2.1 思路12.2 思路2 一、字符串左旋 实现一个函数,可以左旋字符串中的k个字符。 例如: ABCD左旋一个字…...
IntelliJ IDEA使用_常规设置
文章目录 版本说明主题设置取消检查更新依赖自动导入禁止import xxx.*、允许import内部类显示行号、方法分割线、空格代码提示(匹配所有字母)自定义注释颜色添加头部注释自定义字体设置字符编码关联本地GitJDK编译版本Maven配置Tomcat配置代码注释设置头…...

ResponseBodyAdvice 获取参数
废话不多说,简练,一针见血,解决问题,才是最好的。 首先肯定是重写了这个beforeBodyWrite方法 重点来了,获取请求参数: request.getBody()返回一个inputStream流,这里你可以 使用很多方法把这个…...

人力资源服务升级正当时,法大大助力佩信集团加速数字化
人力资源服务业是现代服务业的一个重要门类,在促进就业创业、提供人才服务方面发挥重要作用。同时面对产业转型升级、平台经济快速发展、企业用工成本提高等新形势,发展人力资源服务业对于促进社会化就业、更好发挥我国人力资源优势、服务经济社会发展具…...
UG\NX二次开发 二维向量相加
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 简介: UG\NX二次开发 二维向量相加 效果: 代码: #include "me.hpp"void doIt() {const double vec1[2] = { 1.0,2.0 };const double vec2[2] = { 2.0,2.…...

RabbitMQ深入 —— 持久化和发布确认
前言 前面的文章荔枝梳理了如何去配置RabbitMQ环境并且也介绍了两种比较简单的运行模式,在这篇文章中荔枝将会继续梳理有关RabbitMQ的持久化机制以及发布确认模式的相关知识,希望能够帮助到大家~~~ 文章目录 前言 一、持久化 1.1 队列持久化 1.2 消息…...

人脸识别三部曲
人脸识别三部曲 首先看目录结构图像信息采集 采集图片.py模型训练 训练模型.py人脸识别 人脸识别.py效果 首先看目录结构 引用文121本 opencv │ 采集图片.py │ 训练模型.py │ 人脸识别.py │ └───trainer │ │ trainer.yml │ └───data │ └──…...
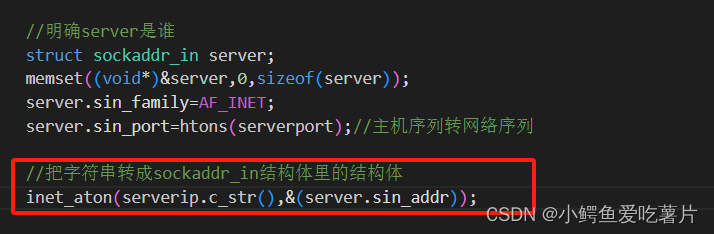
【Linux网络编程】Socket-TCP实例
netstat -nltp 无法用read函数读取UDP套接字的数据,因为UDP是面向数据报,而TCP是面向数据流。 客户端不需要 bind,listen,accept,但是客户端需要connect,connect会自动做bind工作。 #include <sys/sock…...

<OpenCV> 边缘填充
OpenCV边缘填充 1、边缘填充类型 enum cv::BorderTypes ORDER_CONSTANT iiiiii|abcdefgh|iiiiiii with some specified i -常量法,常熟值填充; BORDER_REPLICATE aaaaaa|abcdefgh|hhhhhhh -复制法,复制边缘像素; BORDER_R…...
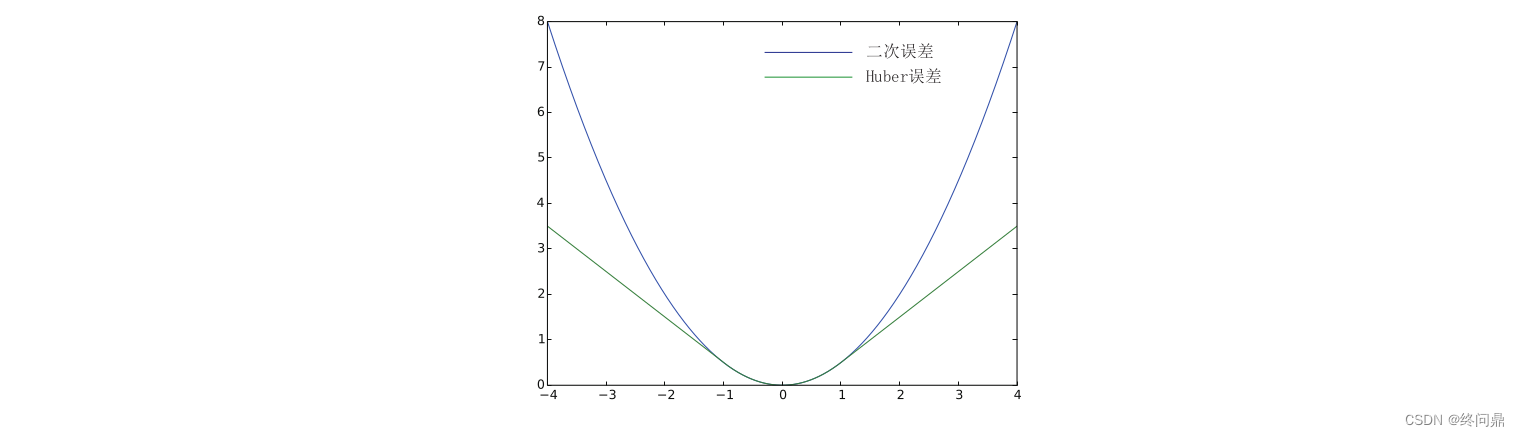
【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端,推导及举例分析
"时间倾诉我的故事" 1. 理论推导2. 主流解法3. 用EKF估计状态3.1. 基于EKF代表解法的感悟 4. 用BA法估计状态4.1 构建最小二乘问题4.2 求解BA推导4.3 H的稀疏结构4.4 根据H稀疏性求解4.5 鲁棒核函数4.6 编程注意 5.总结 引入: 前端里程计能给出一个短时间…...
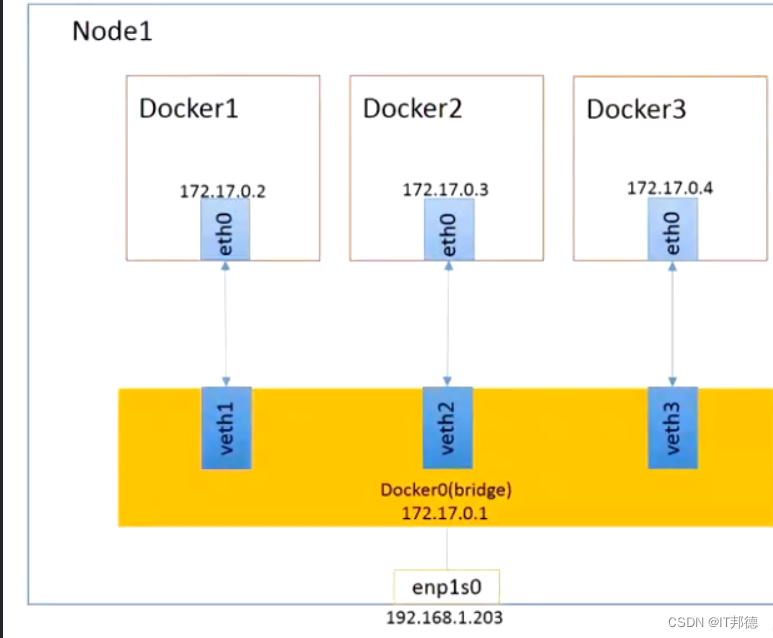
Docker概念通讲
目录 什么是Docker? Docker的应用场景有哪些? Docker的优点有哪些? Docker与虚拟机的区别是什么? Docker的三大核心是什么? 如何快速安装Docker? 如何修改Docker的存储位置? Docker镜像常…...

PHP请求API接口案例采集电商平台数据获取淘宝/天猫优惠券查询示例
优惠券查询API接口对于用户和商家来说具有重要作用,可以方便地获取优惠券信息,进行优惠券搜索和筛选,参与活动和促销推广,提供数据分析和决策支持,提升用户体验和忠诚度,为商家增加销售额和市场竞争力。 t…...
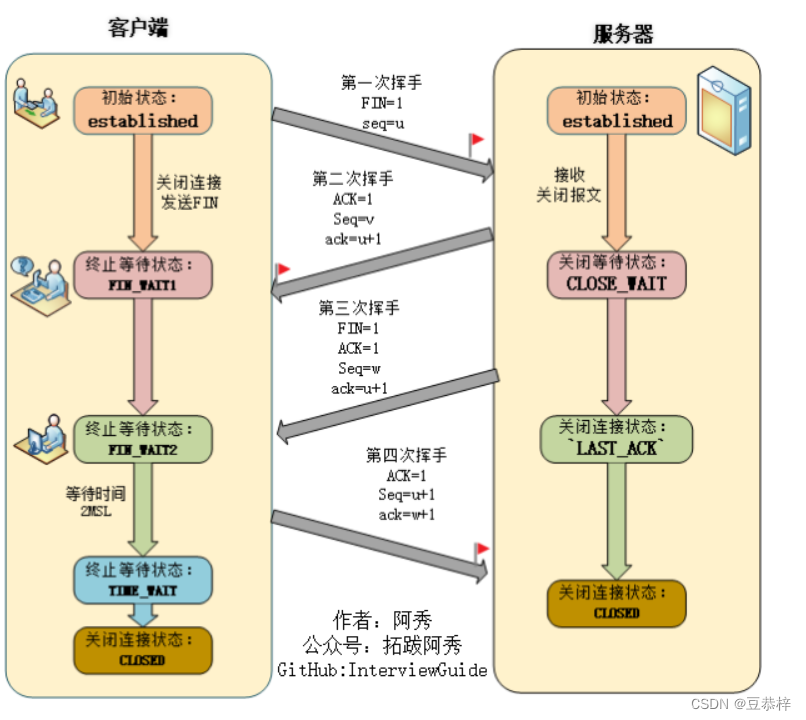
计算机网络:三次握手与四次挥手
摘取作者:拓跋阿秀 三次握手 三次握手(Three-way Handshake)其实就是指建立一个TCP连接时,需要客户端和服务器总共发送3个包。进行三次握手的主要作用就是为了确认双方的接收能力和发送能力是否正常、指定自己的初始化序列号为后…...
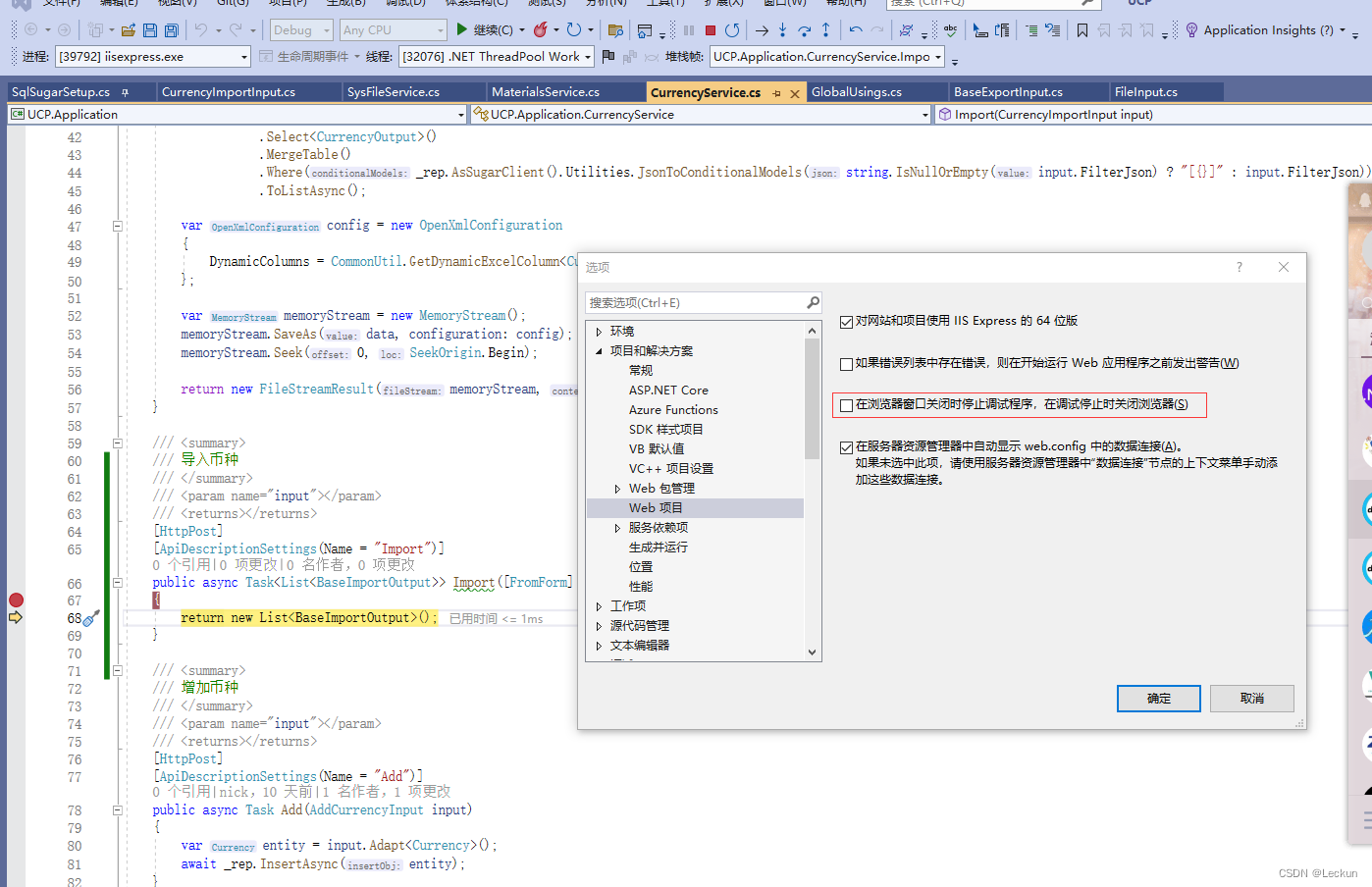
Visual Studio 调试上传文件时自动停止运行的解决方法
进入:选项,项目和解决方案,Web项目, 找到在浏览器窗口关闭时停止调试程序,在调试停止时关闭浏览器 将它不要勾关闭,然后重新启动下Visual Studio,上传文件时就可以调试了...

使用scp命令失败出错
使用scp命令失败出错,无反应。 解决: 1.使用ifconfig查看目标主机公网IP地址 ifconfig需使用公网ip 2.配置免密登录 可参考 远程登录ssh ssh-copy-id root目标主机ip再次尝试scp命令。 SCP(Secure Copy)是一个用于在本地主机和…...
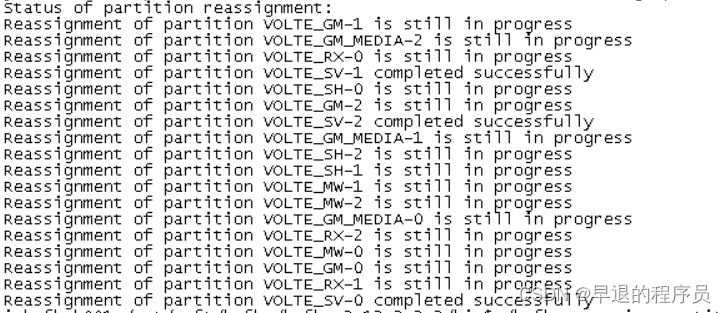
kafka增加磁盘或者分区,topic重分区
场景:kafka配置文件log.dirs增加了几个目录,但是新目录没有分区数据写入,所以打算进行重分区一下。 1.生成迁移计划 进入kafka/bin目录 新建 topic-reassign.json,把要重分区的topic按下面格式写。 { "topics": [{ …...

SpringMVC系列(五)之JSR303和拦截器
目录 一. JSR303 1.1 JSR303是什么 1.2 为什么要使用JSR303 1.3 JSR303常用注解 1.4 JSR303快速入门 1. 导入相关pom依赖 2. 配置校验规则 3. 入门示例 二. SpringMVC的拦截器 2.1 什么是拦截器 2.2 拦截器与过滤器的区别 2.3 拦截器工作原理 2.4 入门示例 1. 创建…...

LCP 01.猜数字
题目来源: leetcode题目,网址:LCP 01. 猜数字 - 力扣(LeetCode) 解题思路: 遍历比较即可。 解题代码: class Solution {public int game(int[] guess, int[] answer) {int res0;for(int …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
