【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端,推导及举例分析
"时间倾诉我的故事"
- 1. 理论推导
- 2. 主流解法
- 3. 用EKF估计状态
- 3.1. 基于EKF代表解法的感悟
- 4. 用BA法估计状态
- 4.1 构建最小二乘问题
- 4.2 求解BA推导
- 4.3 H的稀疏结构
- 4.4 根据H稀疏性求解
- 4.5 鲁棒核函数
- 4.6 编程注意
- 5.总结
引入:
- 前端里程计能给出一个短时间内的轨迹和地图,时间长则不准确;
- 为了得到长时间内最优轨迹和地图,构建一个规模更大的优化问题。在后端优化中,通常考虑更长时间内的状态估计问题。
1. 理论推导
还是摆出最经典的SLAM运动和观测方程
f ( x ) = { x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j f(x)= \begin{cases} x_k = f(x_{k-1}, u_k) + w_k \\ z_{k,j} = h(y_j, x_k) + v_{k,j} \end{cases} f(x)={xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,j
实际上要解决: 拥有某些运动数据 u u u 和观测数据 z z z 时,如何确定状态量 x x x 和 y y y 的分布。
- 解决如下:
令 x k x_k xk 为 k k k 时刻所有的未知量, x k ≜ { x k , y 1 , . . . , y m } x_k \triangleq \{x_k, y_1,...,y_m \} xk≜{xk,y1,...,ym}
同时,令 k 时刻所有的观测值为 z k z_k zk。
代入上式,运动和观测方程以后如下:
f ( x ) = { x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j f(x)= \begin{cases} x_k = f(x_{k-1}, u_k) + w_k \\ z_{k,j} = h(y_j, x_k) + v_{k,j} \end{cases} f(x)={xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,j
在 k k k 时刻,用 0 − k 0-k 0−k 的数据估计现在的状态分布:
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) ⇓ B a y e s 法则交换 z 和 x P ( z k ∣ x k ) P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) ⇓ 按 x k − 1 时刻为条件概率展开 ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 P(x_k|x_0, u_{1:k}, z_{1:k}) \\\;\\\Downarrow Bayes法则交换z和x \\\;\\ P(z_k|x_k)P(x_k|x_0, u_{1:k},z_{1:k-1}) \\\;\\\Downarrow 按x_{k-1}时刻为条件概率展开 \\\;\\ \int P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1})P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1})\, \text d x_{k-1} P(xk∣x0,u1:k,z1:k)⇓Bayes法则交换z和xP(zk∣xk)P(xk∣x0,u1:k,z1:k−1)⇓按xk−1时刻为条件概率展开∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1
2. 主流解法
上式 ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 \int P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1})P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1})\, \text d x_{k-1} ∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1
主流的有两种做法:
-
- 假设马尔科夫性,当前状态仅和上个时态有关,用EKF等滤波器方法做状态估计;前两讲讲到过
-
- 当前状态和之前所有状态都有关系,基于BA用非线性优化等优化框架做。
3. 用EKF估计状态
在马尔科夫性成立后,当前状态仅和上个时态有关,上边左右式可分别简化为(右式中, u k u_k uk 和 k − 1 k-1 k−1 时刻的状态无关,拿掉!):
左边: P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k ∣ x k − 1 , u k ) 右边: P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) 左边:\qquad P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1}) = P(x_k|x_{k-1}, u_k)\\\; \qquad右边:\qquad P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1}) = P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1}) 左边:P(xk∣xk−1,x0,u1:k,z1:k−1)=P(xk∣xk−1,uk)右边:P(xk−1∣x0,u1:k,z1:k−1)=P(xk−1∣x0,u1:k,z1:k−1)
- 由前边的两节知识,可知上式中我们只需维护一个状态量即可,不断迭代更新即可。假设它满足高斯分布,只需要考虑维护状态量的均值和协方差即可。
- 另记: x ^ \hat x x^ 表示先验, x ˉ \bar x xˉ 表示后验
根据高斯分布性质可得EKF中的预测环节:
P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = N ( A k x ˉ k − 1 + u k , A k P ^ k − 1 A k T + R ) = 记为 N ( x ˉ k , P ˉ k ) P(x_k|x_0,u_{1:k}, z_{1:k-1}) = N(A_k\bar x_{k-1}+u_k, \;\;\;A_k\hat P_{k-1}A_k^T+R) = 记为\quad N(\bar x_k, \bar P_k) P(xk∣x0,u1:k,z1:k−1)=N(Akxˉk−1+uk,AkP^k−1AkT+R)=记为N(xˉk,Pˉk)
如此,就可以带入我们的EKF中进行使用。
3.1. 基于EKF代表解法的感悟
运算快,资源低;
局限:
-
- 马尔科夫性质—无法解决类似回环等当前状态与很久之前数据有关的问题
-
- 对 x k x_k xk 在当前时刻的一次线性化,计算出后验概率,是假设该点的线性化在后验概率处还是有效的,实际上不然。只有小范围成立,在远处的地方并不能近似,这是EKF的 非线性误差 。
- 2.1 而在非线性优化方法中,在每迭代一次,状态发生改变后就会做一阶或者二阶近似,重新做泰勒展开,适用范围更加广泛,状态变化大时候也适用。
-
- EKF SLAM不可适用于大场景,landmark多的时候,均值和方差是很大的。
4. 用BA法估计状态
BA(Bundle Adjustment):源于三维重建,在这里的意义是 通过不断调整相机的姿态和特征点的位置,使从每一个特征点反射出来的几束光线都收束到相机中心,类似求解只有观测方程的SLAM问题。
4.1 构建最小二乘问题
针对此问题,观测方程:
z = h ( ξ , p ) z = h(\xi, p) z=h(ξ,p)
ξ \xi ξ 是位姿(李代数表示) , p p p 是路标(特征点的位置), 观测误差如下:
e = z − h ( ξ , p ) e = z - h(\xi, p) e=z−h(ξ,p)
代价函数(Cost Function)如下:
1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ e i j ∣ ∣ 2 = 1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ 2 \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||e_{ij}||^2 = \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||z_{ij}-h(\xi_{i},p_j)||^2 21i=1∑mj=1∑n∣∣eij∣∣2=21i=1∑mj=1∑n∣∣zij−h(ξi,pj)∣∣2
- 其中 z ( i , j ) z(i,j) z(i,j) 表示在位姿 ξ i \xi_i ξi 处观察路标 p j p_j pj 产生的数据。当该式最小时,我们的估计位姿 ξ i \xi_i ξi 和 路标 p j p_j pj 最接近真实值。
为了便于理解这里的 h h h ,举在相机中的例子:
- 这里 h h h 表示将世界坐标下的点 p [ x , y , z ] p[x,y,z] p[x,y,z] 转到像素坐标(也就是程序可读图片的点位置的坐标)下的点 u , v u,v u,v :如下

这就是一个观测方程 h h h 的一种具体参数化的过程。
4.2 求解BA推导
再看要求解的非线性最小二乘问题( h h h 非线性显然 ):
1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ 2 \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||z_{ij}-h(\xi_{i},p_j)||^2 21i=1∑mj=1∑n∣∣zij−h(ξi,pj)∣∣2
首先定义要优化的变量:
x = [ ξ 1 , . . . , ξ m , p 1 , . . . , p n ] T x = [\xi_1, ..., \xi_m,p_1, ..., p_n]^T x=[ξ1,...,ξm,p1,...,pn]T
注意:虽然一个误差项针对的是单个位姿和路标点,但是在整体BA中,必须将优化变量定义为所有待优化的变量。
根据前文:求解非线性问题,要给一个小增量和增量方向,最终要求的也是这个 Δ x \Delta x Δx,这里给增量以后的代价函数为:
1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ e i j + F i j Δ ξ i + E i j Δ p j ∣ ∣ 2 \frac{1}{2}||f(x+\Delta x)||^2 \approx \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||e_{ij}+F_{ij}\Delta \xi_i + E_{ij}\Delta p_j||^2 21∣∣f(x+Δx)∣∣2≈21i=1∑mj=1∑n∣∣eij+FijΔξi+EijΔpj∣∣2
其中 F i j F_{ij} Fij 表示代价函数对相机姿态的偏导数, E i j E_{ij} Eij 表示对路标点位置的偏导数。
将相机位姿,和空间点变量分别放在一起:上式如下:
x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m , x p = [ p 1 , p 2 , . . . , p m ] T ∈ R 3 n ⇓ 1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 = 1 2 ∣ ∣ e + F Δ x c + E Δ x p ∣ ∣ 2 x_c = [\xi_1, \xi_2, ..., \xi_m]^T \in \R^{6m}, \qquad x_p = [p_1, p_2, ..., p_m]^T \in \R^{3n} \\\;\Downarrow\\\;\\ \frac{1}{2}||f(x+\Delta x)||^2 = \frac{1}{2} ||e + F\Delta x_c + E \Delta x_p||^2 xc=[ξ1,ξ2,...,ξm]T∈R6m,xp=[p1,p2,...,pm]T∈R3n⇓21∣∣f(x+Δx)∣∣2=21∣∣e+FΔxc+EΔxp∣∣2
根据前边的非线性优化,最终我们要面临
H Δ x = g H \Delta x = g HΔx=g
而求解它要用的雅克比矩阵可以根据位姿和路标分别定义为:
J = [ F E ] J = [F \quad E] J=[FE]
则:
H = J T J = [ F T F F T E E T F E T E ] H = J^TJ= \begin{bmatrix} F^TF & F^TE \\ E^TF & E^TE \end{bmatrix} H=JTJ=[FTFETFFTEETE]
点越多,就代表这个H的维度越大,计算复杂,资源占得多,接下来分析如何观察这个 H H H 的特点。
4.3 H的稀疏结构
根据前边,我们知道 H = J T J H = J^TJ H=JTJ, H H H的研究放在 J J J 上,对于J,考虑一个 e i j e_{ij} eij 它的表述如下:
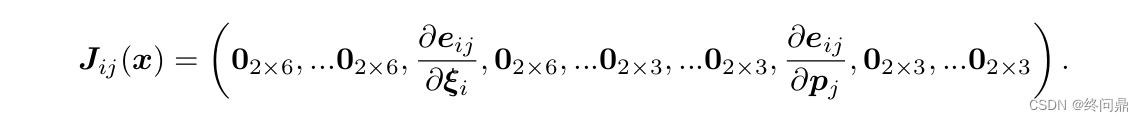
几何意义就是:它只涉及第 i 个矩阵和第 j 个路标,其余都为0,描述的是 ξ i \xi_i ξi看到 p j p_j pj 这件事,且前边的是位姿导数(6维),后边的是路标(三维)。
- 举例说明
假设有2个相机,6个路标。可视化它们的关系如下(可以观测到,则底下用实线连接):
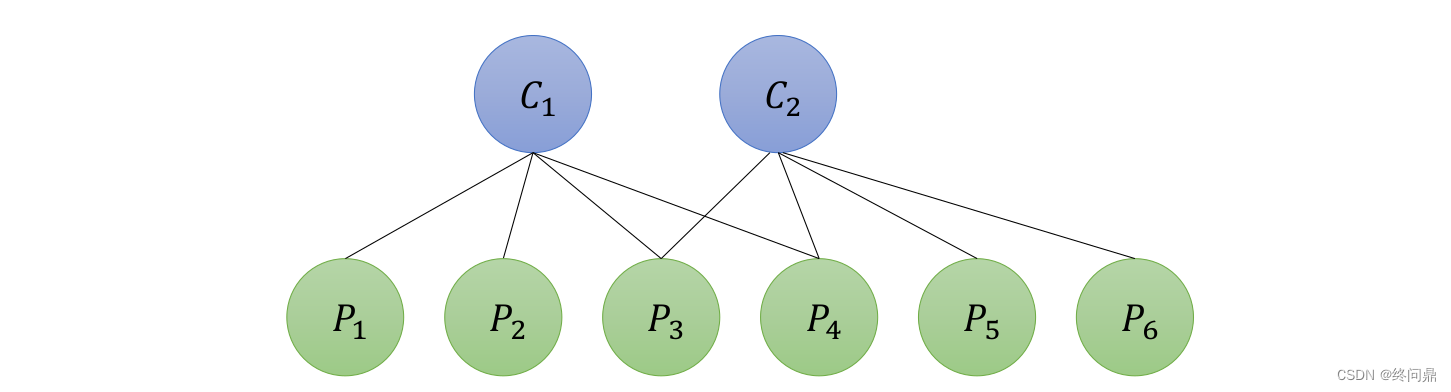 根据上边,把 C 1 C_1 C1 观察到 P 1 P_1 P1 的雅克比直观出来,则如下,因为 C 1 C_1 C1 六维:
根据上边,把 C 1 C_1 C1 观察到 P 1 P_1 P1 的雅克比直观出来,则如下,因为 C 1 C_1 C1 六维:
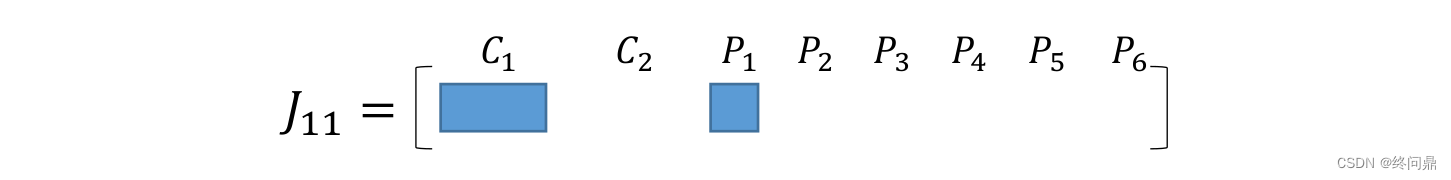
这个时候,将所有 J i j J_{ij} Jij 和 它们相乘之后的 H H H 同样直观展示:
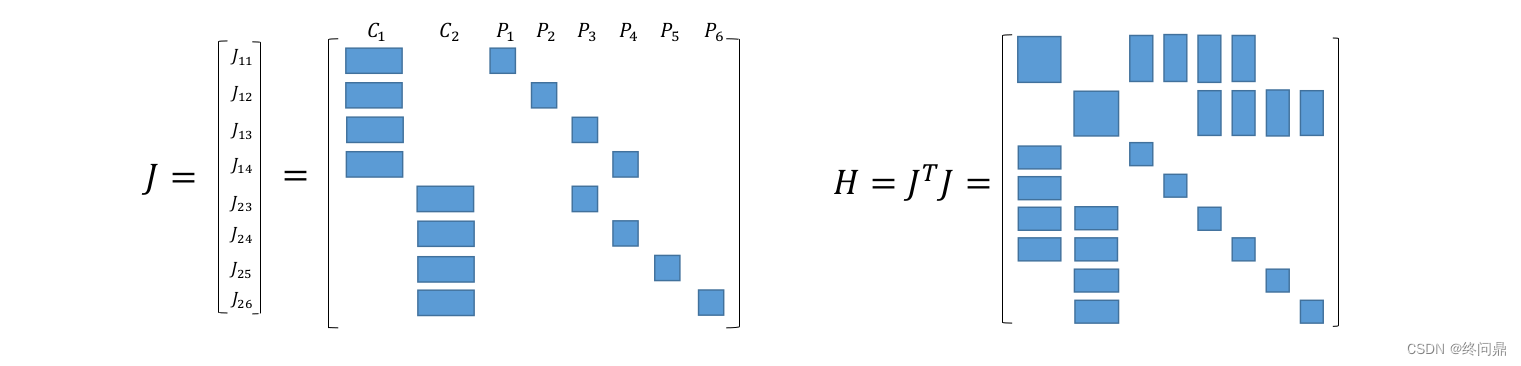
我们发现:H对应邻接矩阵,可以知道 假如 C i C_i Ci 可以观察到 P j P_j Pj ,那么 H i j H_{ij} Hij 则是有值的,否则是为0.如下:
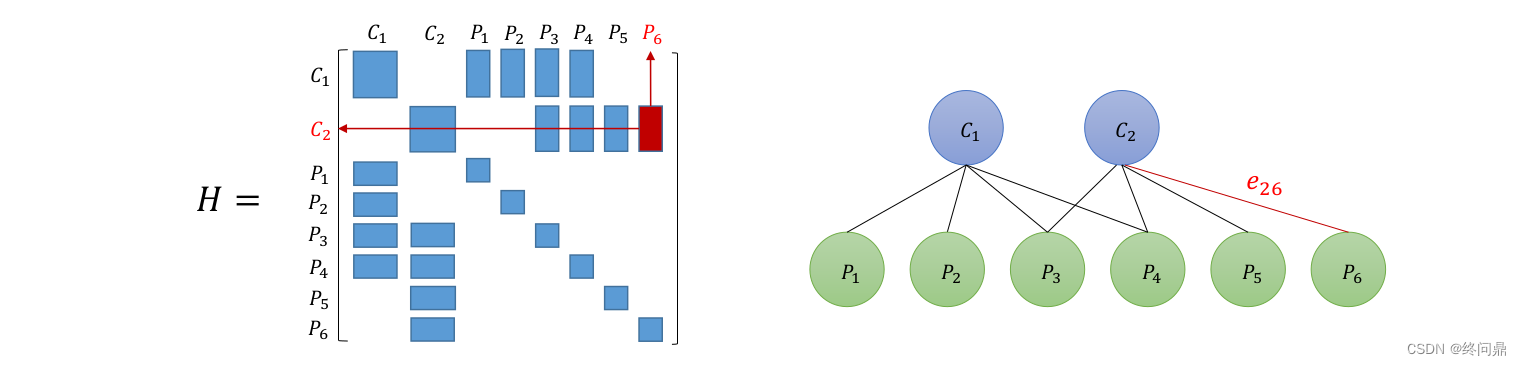
4.4 根据H稀疏性求解
根据以上H性质,可以将H分块为:其中 B B B 纯位姿, C C C对角线纯路标,B非对角非零表示共视关系:
H = [ B E E T C ] H = \begin{bmatrix} B & E \\ E^T & C \end{bmatrix} H=[BETEC]
这个时候就可以求解 H Δ x = g H \Delta x = g HΔx=g 这个方程:
[ B E E T C ] [ Δ x c Δ x p ] = [ v w ] \begin{bmatrix} B & E \\ E^T & C \end{bmatrix} \begin{bmatrix}\Delta x_c \\ \Delta x_p\end{bmatrix} = \begin{bmatrix} v \\w \end{bmatrix} [BETEC][ΔxcΔxp]=[vw]
此时通过Schur消元(也叫边缘化)—就是先求一个比如 Δ x c \Delta x_c Δxc 然后再反代回去求 Δ x p \Delta x_p Δxp 的方法去求解。
4.5 鲁棒核函数
- 说明问题:我们采用的是误差项的二范数平方和,如果出现误匹配,单个项的误差就很大,此时优化算法会均摊误差去调整其他正确的数据。
- 问题原因:误差很大时,二范数增长过快(平方嘛)
- 解决:鲁棒核函数–把二范数度量换成增长较低,同时保证光滑(求导要求)的表述,因为它使得整个优化结果更为鲁棒,所以又叫它鲁棒核函数(Robust Kernel)。
列举一个常见的鲁棒核函数,Huber核:
f ( x ) = { 1 2 e 2 i f ∣ e ∣ ≤ δ , δ ( ∣ e ∣ − 1 2 δ ) o t h e r w i s e . f(x)= \begin{cases} \frac{1}{2}e^2 \qquad\qquad\qquad if|e| \le \delta, \\ \delta(|e| - \frac{1}{2} \delta)\qquad\quad otherwise . \end{cases} f(x)={21e2if∣e∣≤δ,δ(∣e∣−21δ)otherwise.
它的图像如下:
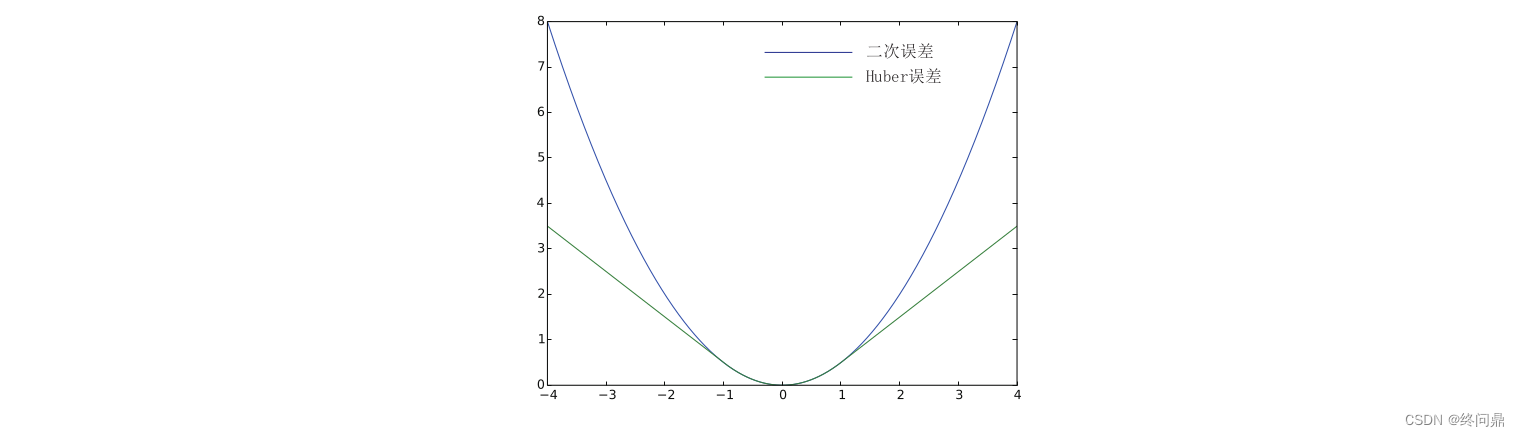
此外还有Cauchy核,Tukey核等。
4.6 编程注意
在使用G2O求解时,所有点云都要进行Schur,因为定义的Matrix维度仅仅是相机姿态参数的维度,要确保它不包含其他路标维度,不然报错。
5.总结
- 假设马尔科夫,EKF代表的滤波器模型
- 考虑所有状态,构成最小二乘问题,只有观测时又称BA。
相关文章:

【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端,推导及举例分析
"时间倾诉我的故事" 1. 理论推导2. 主流解法3. 用EKF估计状态3.1. 基于EKF代表解法的感悟 4. 用BA法估计状态4.1 构建最小二乘问题4.2 求解BA推导4.3 H的稀疏结构4.4 根据H稀疏性求解4.5 鲁棒核函数4.6 编程注意 5.总结 引入: 前端里程计能给出一个短时间…...
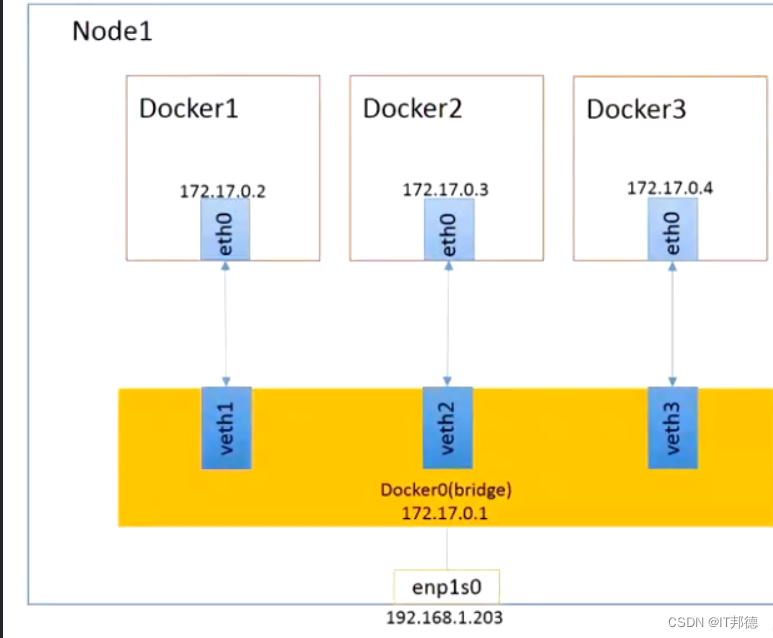
Docker概念通讲
目录 什么是Docker? Docker的应用场景有哪些? Docker的优点有哪些? Docker与虚拟机的区别是什么? Docker的三大核心是什么? 如何快速安装Docker? 如何修改Docker的存储位置? Docker镜像常…...

PHP请求API接口案例采集电商平台数据获取淘宝/天猫优惠券查询示例
优惠券查询API接口对于用户和商家来说具有重要作用,可以方便地获取优惠券信息,进行优惠券搜索和筛选,参与活动和促销推广,提供数据分析和决策支持,提升用户体验和忠诚度,为商家增加销售额和市场竞争力。 t…...
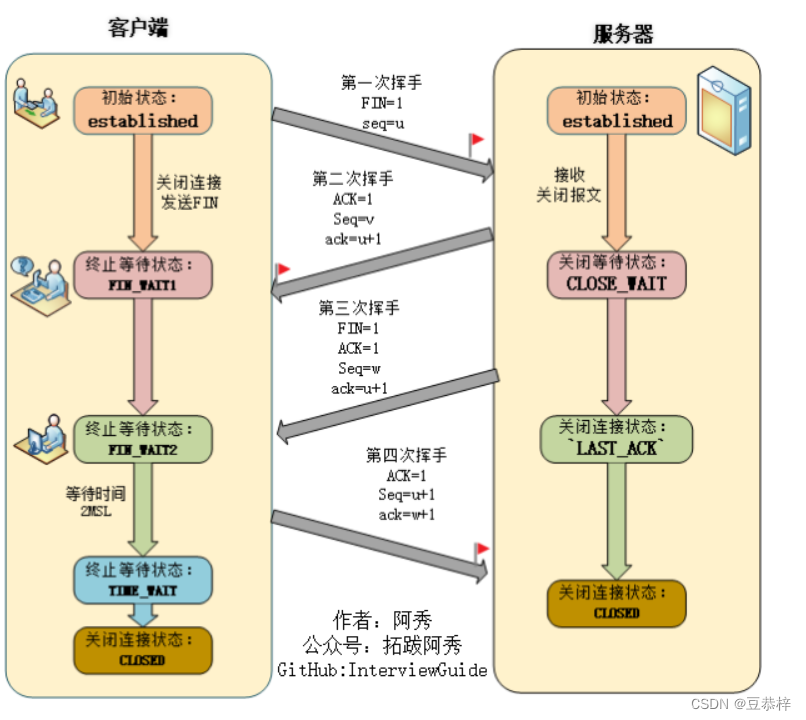
计算机网络:三次握手与四次挥手
摘取作者:拓跋阿秀 三次握手 三次握手(Three-way Handshake)其实就是指建立一个TCP连接时,需要客户端和服务器总共发送3个包。进行三次握手的主要作用就是为了确认双方的接收能力和发送能力是否正常、指定自己的初始化序列号为后…...
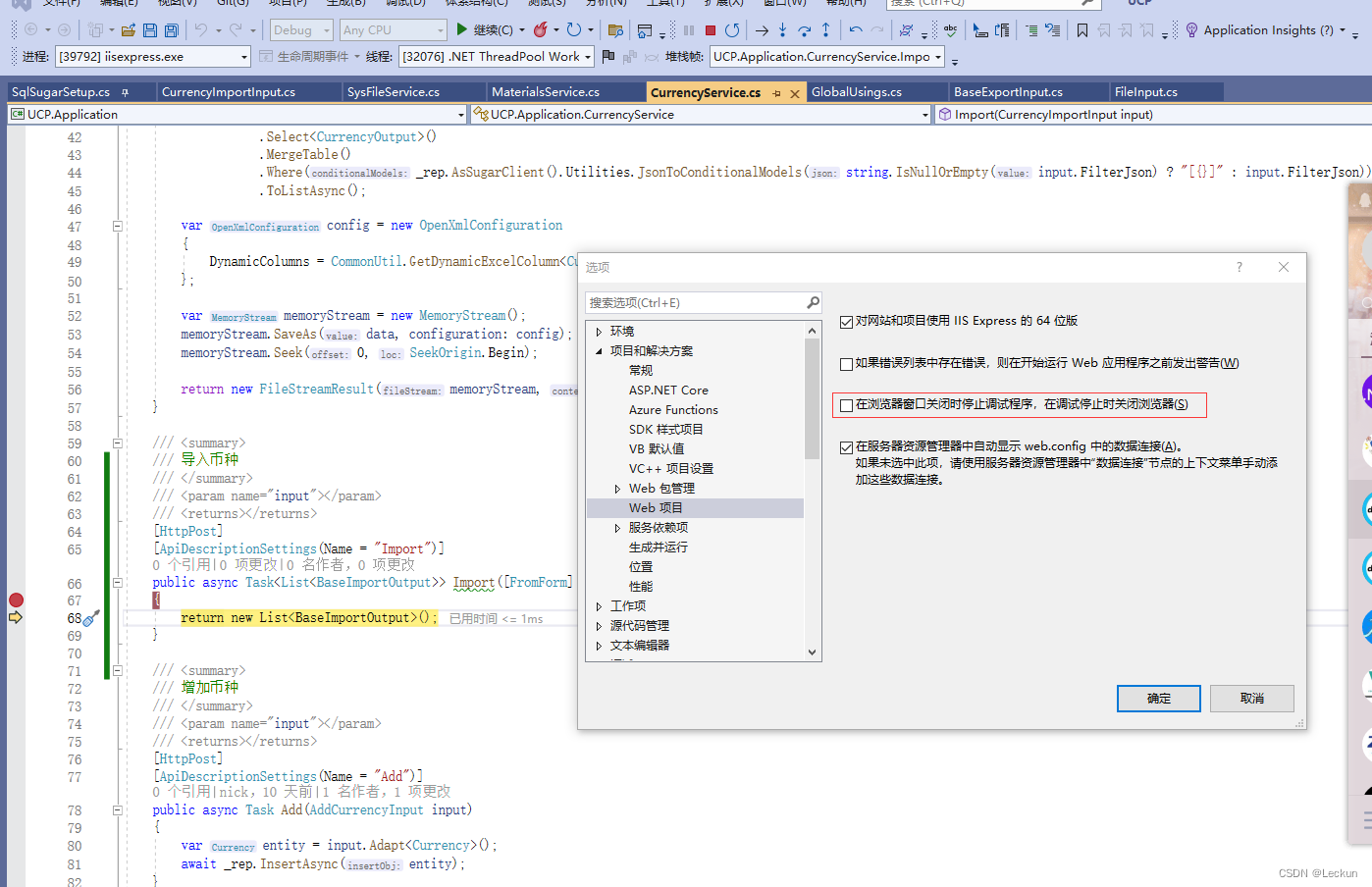
Visual Studio 调试上传文件时自动停止运行的解决方法
进入:选项,项目和解决方案,Web项目, 找到在浏览器窗口关闭时停止调试程序,在调试停止时关闭浏览器 将它不要勾关闭,然后重新启动下Visual Studio,上传文件时就可以调试了...

使用scp命令失败出错
使用scp命令失败出错,无反应。 解决: 1.使用ifconfig查看目标主机公网IP地址 ifconfig需使用公网ip 2.配置免密登录 可参考 远程登录ssh ssh-copy-id root目标主机ip再次尝试scp命令。 SCP(Secure Copy)是一个用于在本地主机和…...
kafka增加磁盘或者分区,topic重分区
场景:kafka配置文件log.dirs增加了几个目录,但是新目录没有分区数据写入,所以打算进行重分区一下。 1.生成迁移计划 进入kafka/bin目录 新建 topic-reassign.json,把要重分区的topic按下面格式写。 { "topics": [{ …...

SpringMVC系列(五)之JSR303和拦截器
目录 一. JSR303 1.1 JSR303是什么 1.2 为什么要使用JSR303 1.3 JSR303常用注解 1.4 JSR303快速入门 1. 导入相关pom依赖 2. 配置校验规则 3. 入门示例 二. SpringMVC的拦截器 2.1 什么是拦截器 2.2 拦截器与过滤器的区别 2.3 拦截器工作原理 2.4 入门示例 1. 创建…...

LCP 01.猜数字
题目来源: leetcode题目,网址:LCP 01. 猜数字 - 力扣(LeetCode) 解题思路: 遍历比较即可。 解题代码: class Solution {public int game(int[] guess, int[] answer) {int res0;for(int …...

智能小车开发
1.材料 店铺:店内搜索页-risym旗舰店-天猫Tmall.com 1.四个小车轮子 2.四个直流减速电机 3.两节18650锂电池(每节3.7V),大概电压在7.4V左右,电压最好不要超过12V不然会损坏电机驱动 4.一个18650锂电池盒 5.一个L…...

RDMA性能测试工具集preftest_README
文章目录 1 概述2 安装3 测试方法说明4 测试说明5 运行测试所有测试的通用选项延迟测试选项带宽测试选项ib_send_lat(发送延迟测试)和 ib_send_bw(发送带宽测试)的选项ib_atomic_lat(原子延迟测试)和 ib_at…...

墨天轮专访星环科技刘熙:“向量热”背后的冷思考,Hippo如何打造“先发”优势?
导读: 深耕技术研发数十载,坚持自主可控发展路。星环科技一路砥砺前行、坚持创新为先,建设了全面的产品矩阵,并于2022年作为首个独立基础软件产品公司成功上市。星环科技在今年的向星力•未来技术大会上发布了分布式向量数据库Tra…...

逆向-beginners之非递归
/* * 非递归 */ void f() { } void main() { f(); } #if 0 /* * intel */ 0000000000001129 <f>: 1129: f3 0f 1e fa endbr64 112d: 55 push %rbp 112e: 48 89 e5 mov %rsp,%…...

Spring for Apache Kafka概述和简单入门
一、概述 Spring for Apache Kafka 的高级概述以及底层概念和可运行的示例代码。 二、准备工作 注意:进行工作开始之前至少要有一个 Apache Kafka 环境 2.1、依赖 使用 Spring Boot<dependency><groupId>org.springframework.kafka</groupId><artifact…...
基于SSM+Vue的医院医患管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用Vue技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
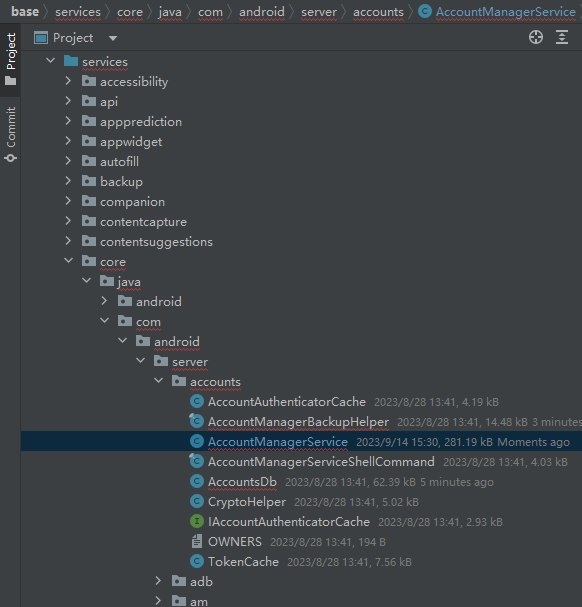
再次理解Android账号管理体系
目录 ✅ 0. 需求 📂 1. 前言 🔱 2. 使用 2.1 账户体系前提 2.2 创建账户服务 2.3 操作账户-增删改查 💠 3. 源码流程 ✅ 0. 需求 试想,自己去实现一个账号管理体系,该如何做呢? ——————————…...
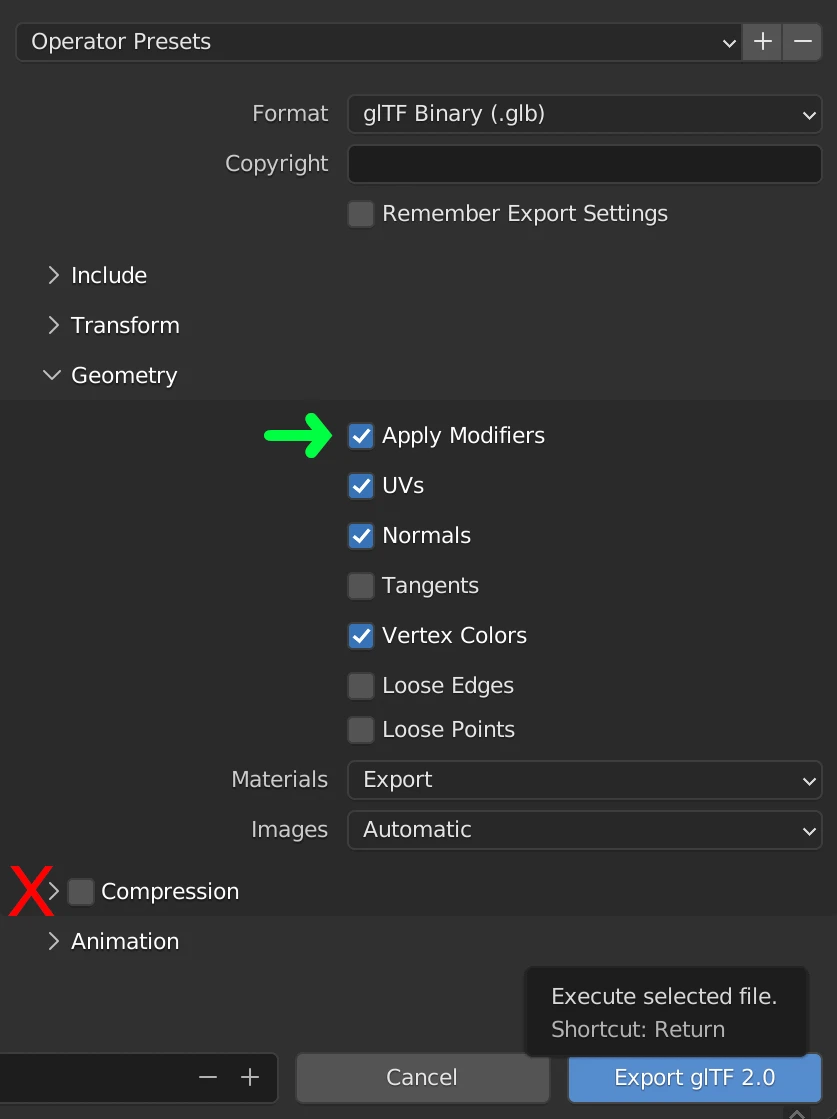
如何在Blender中压缩/减小GLTF模型的大小
GLTF 如何在Blender中压缩/减小GLTF模型的大小 Blender是一款功能强大的开源软件,旨在创建3D图形,动画和视觉效果。它支持多种文件格式的导入和导出,包括GLB,GLTF,DAE,OBJ,ABC,USD…...

IntelliJ IDEA使用_Plugin插件推荐
官网插件库:https://plugins.jetbrains.com/search 代码规范检测:Alibaba Java Coding Guidelines码云:Giteemybatis插件:MyBatisX多颜色括号:Rainbow Brackets操作快捷键提示:Key Promoter X力扣ÿ…...
Ajax fetch navigator.sendBeacon 三个的区别
Ajax、fetch 和 navigator.sendBeacon 是用于发送网络请求的不同方法。 Ajax: Ajax 是一种传统的用于发送异步请求的技术。它使用 XMLHttpRequest 对象来发送数据和接收响应。通过创建 XMLHttpRequest 对象,你可以通过调用其 open() 方法指定请求的类型和 URL&#…...

map-reduce执行过程
Map阶段 Map 阶段是 MapReduce 框架中的一个重要阶段,它负责将输入数据转换为中间数据。Map 阶段由一个或多个 Map 任务组成,每个 Map 任务负责处理输入数据的一个子集。 执行步骤 Map 阶段的过程可以分为以下几个大步骤: 输入数据分配&a…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
