排序算法-归并排序
属性
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使 子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
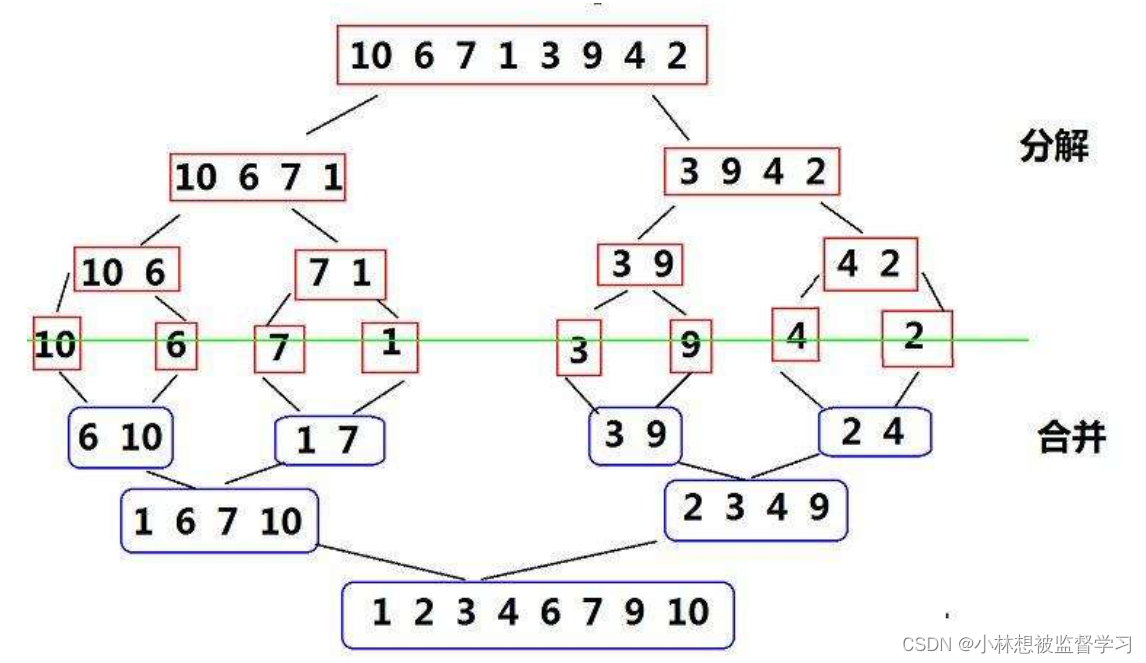 归并排序总结
归并排序总结
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
代码及注释(递归实现)
//mergeSort是归并排序提供使用的方法public static void mergeSort(int[]arr){//用mergeSortChild进行递归排序mergeSortChild(arr,0,arr.length-1);}private static void mergeSortChild(int[]arr,int left,int right){//出递归if(left>=right){return;}//先计算出要排序数据的中间位置int mid=(left+right)/2;//先分别归并排序左边和右边的数据,排序好以后再将左边和右边的数据合并mergeSortChild(arr,left,mid);mergeSortChild(arr,mid+1,right);merge(arr,left,right);}private static void merge(int[]arr,int left,int right){int mid=(left+right)/2;//left和right范围的数据分为了两个部分//用s1,e1表示第一部分的数据范围,s2,e2表示第二部分的数据范围//两个部分的数据分别是排序好了的,要将两个部分的数据进行合并int s1=left;int e1=mid;int s2=mid+1;int e2=right;//定义辅助数组help来帮助合并int[]help=new int[right-left+1];//放数据的时候有以下的几种情况//1.两个部分的数据还没有哪个部分全放到help数组中int k=0; //k是用于指向help数组的下标while (s1<=e1&&s2<=e2){//当s1下标的数据比s2下标的小时,s1下标的数据就先放到help数组中if(arr[s1]<arr[s2]){help[k++]=arr[s1++];}else {help[k++]=arr[s2++];}}//2.s1>e1 第一部分的数据都放到了help数组中//直接将第二部分的数据全放到help数组中while (s2<=e2){help[k++]=arr[s2++];}//3.s2>e1 第二部分的数据都放到了help数组中//直接将第一部分的数据全放到help数组中while (s1<=e1){help[k++]=arr[s1++];}//此时两个部分的数据都放到了help数组中//将数组中对应部分的数据改为help数组中的数据(help数组中的数据是合并好了的)for(int i=left,j=0;i<=right;i++,j++){arr[i]=help[j];}}代码及注释(非递归实现)
//归并排序---非递归public static void mergeSortNo(int[] array){//一个数据为一组int gap=1;while (gap<array.length){for(int i=0;i<array.length;i+=2*gap){int left=i;int mid=left+gap-1;int right=mid+gap;merge(array,left,mid,right);}gap=gap*2;}} //合并private static void merge(int[] array,int left,int mid,int right){int s1=left;int e1=mid;int s2=mid+1;int e2=right;//定义辅助数组int[]help=new int[right-left+1];int k=0;//两组数据都没放完while (s1<=e1&&s2<=e2){if(array[s1]<array[s2]){help[k++]=array[s1++];}else {help[k++]=array[s2++];}}//当有一组中的数据放完while (s1<=e1){help[k++]=array[s1++];}while (s2<=e2){help[k++]=array[s2++];}//将合并好的数据返回给数组arrayfor (int i=0;i<help.length;i++){array[left+i]=help[i];}}
相关文章:

排序算法-归并排序
属性 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序&#…...

vue3 整合 springboot 打完整jar包
前端 .env.developmen VITE_APP_BASE_URL/api.env.production VITE_APP_BASE_URL/axios 配置 axios.defaults.baseURL import.meta.env.VITE_APP_BASE_URLpackage.json "scripts": {"dev": "vite --mode development","build": &…...

依赖倒转原则是什么?
依赖倒转原则(Dependency Inversion Principle)是面向对象设计中的另一个基本原则,它是由Robert C. Martin提出的,它的中心思想是面向接口编程,该原则指出高层模块不应该依赖于低层模块,两者都应该依赖于抽…...

什么是GPT与MBR
GPT(GUID Partition Table)和MBR(Master Boot Record)是两种不同的磁盘分区表格式。 MBR是一种较早的磁盘分区表格式,它使用512字节的扇区作为存储空间。MBR分区表可以定义最多4个主分区,每个主分区都可以…...

前后端开发接口联调对接参数
前言 一个完整的互联网系统项目,需要前后端配合,进行上线,针对前端开发者,现在互联网主流的项目都是前后端分离 也就是后端负责提供数据接口,前端负责UI界面数据渲染 凡是在前台数据展示与用户交互的,都是由前端来实现的,而数据来源是由后台服务提供的 在浏览器c端能够发送后端…...

定时任务框架-xxljob
1.定时任务 spring传统的定时任务Scheduled,但是这样存在这一些问题 : 做集群任务的重复执行问题 cron表达式定义在代码之中,修改不方便 定时任务失败了,无法重试也没有统计 如果任务量过大,不能有效的分片执行 …...
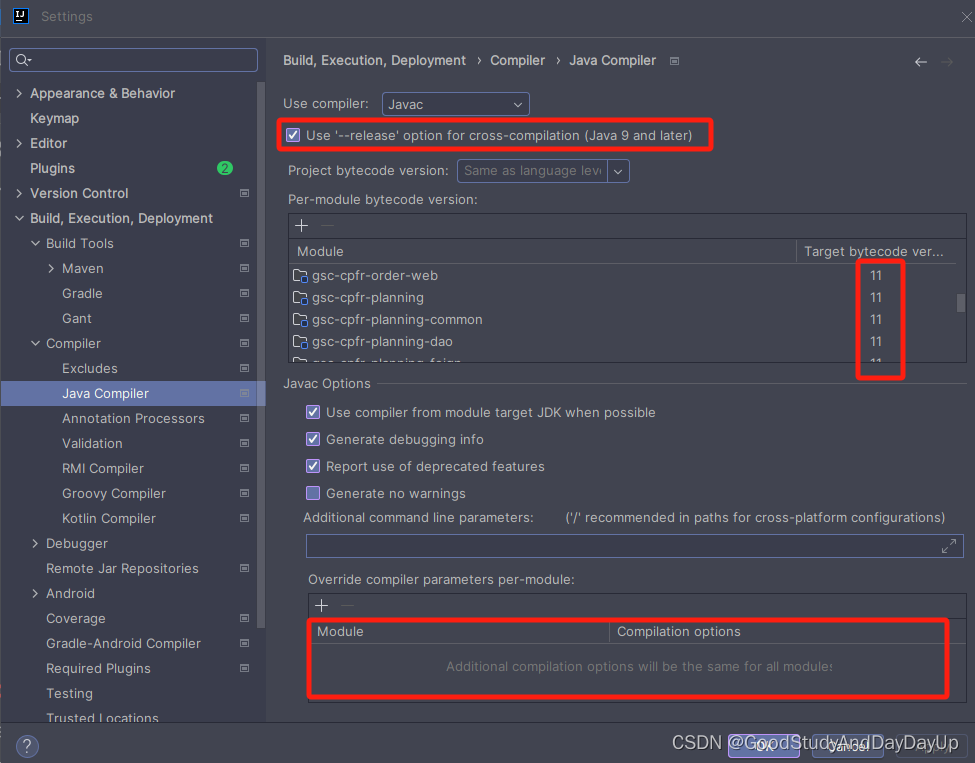
idea项目配置三大步
场景: 使用 idea 打开一个新项目的时候,想让项目迅速跑起来, 其实只需要下面简单三步: 1. 首先,配maven 2. 其次,配置 jdk 这里配置 project 就行了,不用管Modules中的配置。 3. 最后&#…...

学会SpringMVC之自定义注解各种场景应用,提高开发效率及代码质量
目录 一、简介 ( 1 ) 是什么 ( 2 ) 分类 ( 3 ) 作用 二、自定义注解 ( 1 ) 如何自定义注解 ( 2 ) 场景演示 场景一(获取类与方法上的注解值) 场景二( 获取类属性上的注解属性值 ) 场景三( 获取参数修…...
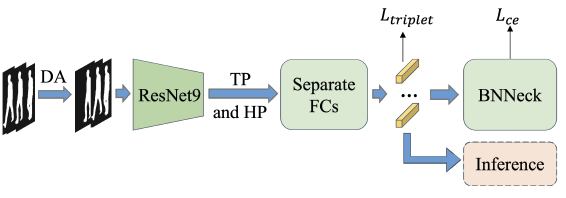
步态识别常见模块解读及代码实现:基于OpenGait框架
步态识别常见模块解读及代码实现:基于OpenGait框架 最近在看步态识别相关论文,但是因为记忆力下降的原因,老是忘记一些内容。因此记录下来方便以后查阅,仅供自己学习参考,没有背景知识和论文介绍。 目录 步态识别常见…...

前端八股文之“闭包”
一、定义 一句话概括闭包:能够访问函数内部变量的函数与这个变量的组合构成了闭包结构。如下代码 function fuc1(){let num 999return function fuc2(){console.log(num)}}fuc1()(); 如代码所示,fuc2和父级变量num构成了一个闭包环境。 二、原理 子…...

数据可视化:掌握数据领域的万金油技能
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...
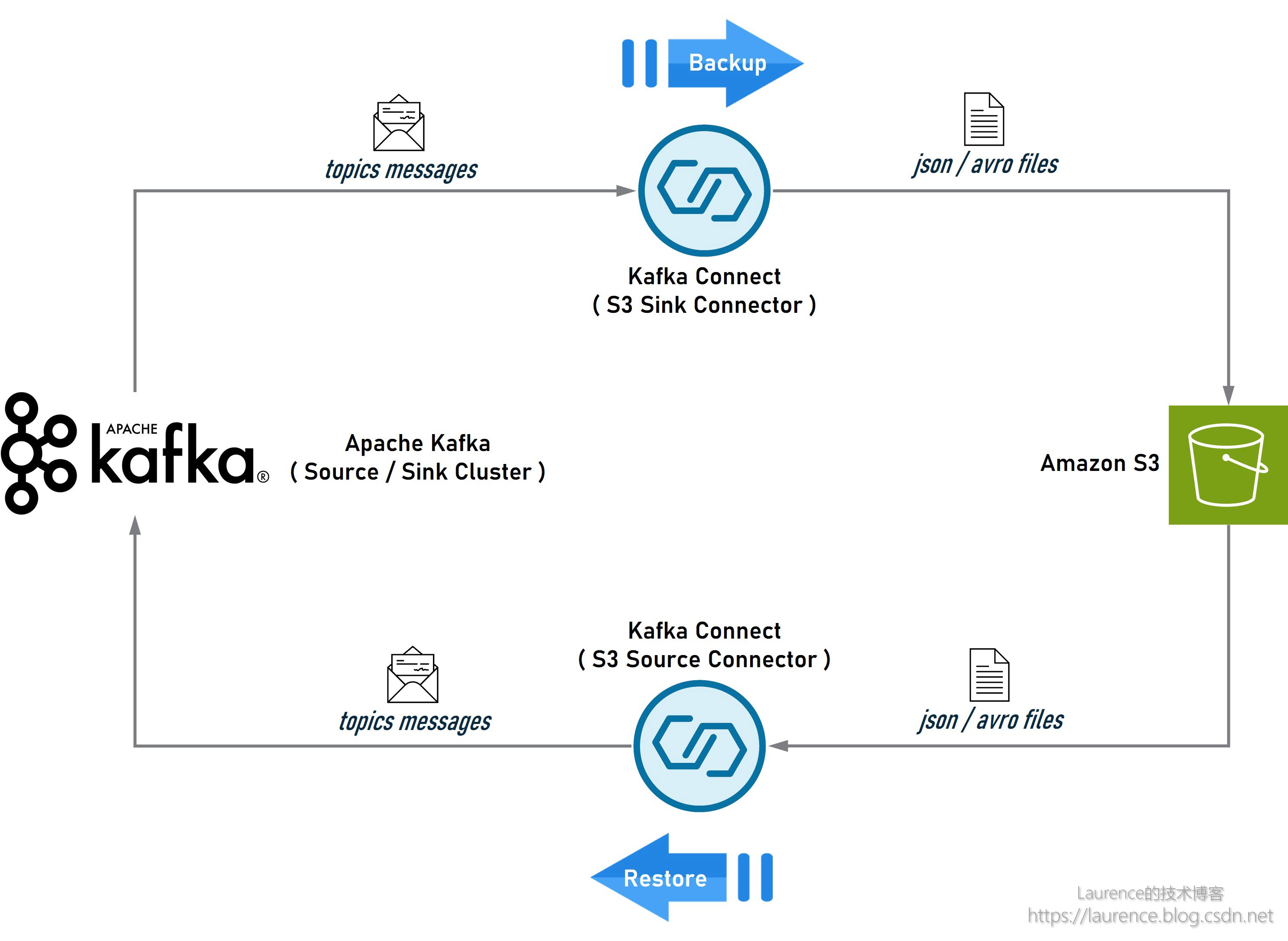
Apache Kafka 基于 S3 的数据导出、导入、备份、还原、迁移方案
在系统升级或迁移时,用户常常需要将一个 Kafka 集群中的数据导出(备份),然后在新集群或另一个集群中再将数据导入(还原)。通常,Kafka集群间的数据复制和同步多采用 Kafka MirrorMaker࿰…...

事务管理AOP
事务管理 事务回顾 概念:事务是一组操作的集合,它是一个不可分割的工作单位,这些操作要么同时成功,要么同时失败 操作: 开启事务:一组操作开始前,开启事务-start transaction/be…...

Java从Tif中抽取最大的那张图进行裁剪成x*y份
之前我有一篇帖子《kfb格式文件转jpg格式》讲述到 kfb > tif > jpg,但是针对于超大tif中的大图是无法顺利提取的,就算是能顺利提取,试想一下,2G的tif文件,如果能提取处理最大的那张图,并且在不压缩的…...

人工智能AI界的龙头企业,炸裂的“英伟达”时代能走多远
原创 | 文 BFT机器人 1、AI芯片的竞争格局已趋白热化 尽管各类具有不同功能和定位的AI芯片在一定程度上可实现互补,但同时也在机遇与挑战并存中持续调整定位。在AI训练端,英伟达的GPU凭着高算力的门槛,一直都是训练端的首选。 只有少数芯片能…...

【实战】H5 页面同时适配 PC 移动端 —— 旋转横屏
文章目录 一、场景二、方案三、书单推荐01 《深入实践Kotlin元编程》02 《Spring Boot学习指南》03 《Kotlin编程实战》 一、场景 一个做数据监控的单页面,页面主要内容是一个整体必须是宽屏才能正常展示,这时就不能用传统的适配方案了,需要…...
使用凌鲨进行聚合搜索
作为研发人员,我们经常需要在多个来源之间查找信息,以便进行研发工作。除了常用的搜索引擎如百度和必应之外,我们还需要查阅各种代码文档和依赖包等资源。这些资源通常分散在各个网站和文档库中,需要花费一定的时间和精力才能找到…...

程序设计之——手把手教你如何从Excel文件中读取学生信息
在当今信息化时代,计算机技术已经深入到各个领域,而程序设计则成为推动信息化建设的关键技术之一。在众多领域中,学生信息管理系统无疑是其中一个重要的应用。本文将从学生信息管理系统的开发入手,探讨开如何高效且保证质量的完成…...

Docker容器化技术(从零学会Docker)
文章目录 前言一、初识Docker1.初识Docker-Docker概述2.初识Docker-安装Docker3.初识Docker-Docker架构4.初识Docker-配置镜像加速器 二、Docker命令1.Docker命令-服务相关命令2.Docker命令-镜像相关命令3.Docker命令-容器相关命令 三、Docker容器的数据卷1.Docker容器数据卷-数…...

【新版】系统架构设计师 - 案例分析 - 总览
个人总结,仅供参考,欢迎加好友一起讨论 架构 - 案例分析 - 总览 新旧大纲对应 旧版新版系统规划软件架构设计设计模式系统设计系统建模分布式系统设计嵌入式系统设计系统的可靠性分析与设计系统的安全性和保密性设计系统计划信息系统架构的设计理论和实…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
