9.15 滴滴笔试
T1(二分)
#include <bits/stdc++.h>#define endl '\n'using namespace std;typedef long long LL;const int N = 1e5 + 10;int n, k;
int a[N];bool check(int mid) {int rec = 1e9, cnt = 1;for(int i = 0; i < n; i ++) {int j = i;while(j < n && a[j] - a[i] < mid) j ++ ;if(j < n) rec = min(rec, a[j] - a[i]), cnt ++;i = j - 1;}return cnt >= k && rec >= mid;
}void solve() {cin >> n >> k;for(int i = 0; i < n; i ++) cin >> a[i];int l = 1, r = 1e6 + 10;while(l < r) {int mid = l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << r << endl;
}int main() {cin.tie(0); cout.tie(0);std::ios::sync_with_stdio(false);int T = 1;
// cin >> T;while(T --) {solve();}return 0;
}
T2(01BFS)
#include <bits/stdc++.h>#define x first
#define y second#define endl '\n'using namespace std;typedef long long LL;
typedef pair<int, int> PII;const int N = 1e5 + 10;int n, m;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};void solve() {cin >> n >> m;vector<vector<int>> g(n, vector<int> (m));vector<vector<int>> dist(n, vector<int> (m, 1e9));for(int i = 0; i < n; i ++) {for(int j = 0; j < m; j ++) {cin >> g[i][j];}}deque<PII> q;q.push_back({0, 0});dist[0][0] = g[0][0];while(q.size()) {auto t = q.front(); q.pop_front();int x = t.x, y = t.y;for(int i = 0; i < 4; i ++) {int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m) {if(dist[a][b] > dist[x][y] + g[a][b]) {dist[a][b] = dist[x][y] + g[a][b];if(g[a][b] == 1) {q.push_back({a, b});} else {q.push_front({a, b});}}}}}cout << dist[n - 1][m - 1] << endl;
}int main() {cin.tie(0); cout.tie(0);std::ios::sync_with_stdio(false);int T = 1;
// cin >> T;while(T --) {solve();}return 0;
}
相关文章:

9.15 滴滴笔试
T1(二分) #include <bits/stdc.h>#define endl \nusing namespace std;typedef long long LL;const int N 1e5 10;int n, k; int a[N];bool check(int mid) {int rec 1e9, cnt 1;for(int i 0; i < n; i ) {int j i;while(j < n &…...
有趣的设计模式——适配器模式让两脚插头也能使用三孔插板
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 场景与问题 众所周知,我们国家的生活用电的电压是220V而笔记本电脑、手机等电子设备的工作压没有这么高。为了使笔记本、手机等设备可以使用220V的生活用电就需…...
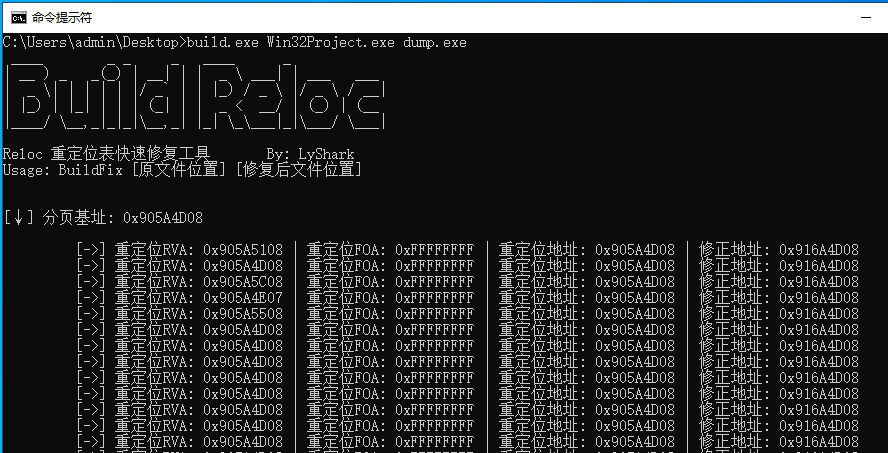
2.10 PE结构:重建重定位表结构
Relocation(重定位)是一种将程序中的一些地址修正为运行时可用的实际地址的机制。在程序编译过程中,由于程序中使用了各种全局变量和函数,这些变量和函数的地址还没有确定,因此它们的地址只能暂时使用一个相对地址。当…...
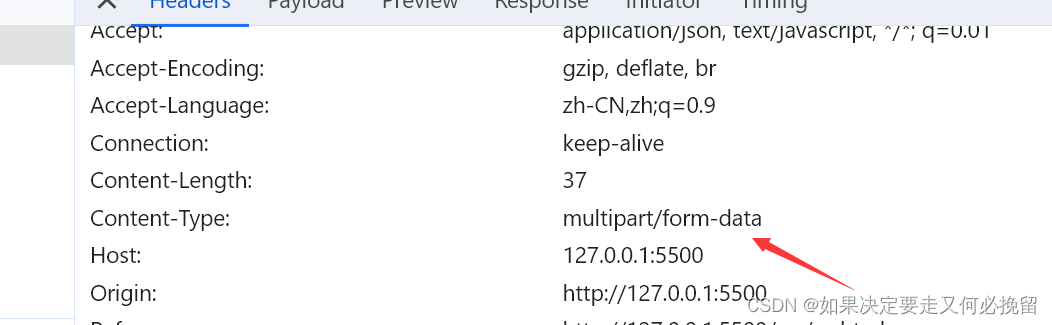
关于content-type的理解
一.content-type的结论 告诉后端传过去的数据是什么类型的数据 二.没有请求体 (1)没有请求体的情况下content-type没有意义。 (2):图示 里面是没有请求体的 (3)有请求体的情况 二.常见的三种方式 (1)application/x-www-form-urlencoded(默认) 参数的表现形式: 传递之前可以…...

<图像处理> 空间滤波基础二
空间滤波基础二:锐化 锐化的作用的突出灰度中的过渡。图像锐化通过空间微分来实现,微分将增强边缘和其他不连续(噪声),不强化灰度变化缓慢的区域。图像锐化也叫做高通滤波,通过高频,抑制低频。…...

Java中的队列Queue
Queue(队列)是一种在计算机科学中常见的数据结构,它基于先进先出(FIFO)的原则,即最先进入队列的元素最先出队。在Java中,Queue是一个接口,定义了一组操作队列的方法,而具体的实现类可以选择性地实现这些方法。 以下是Queue的一些常见用途和操作: 添加元素: 使用off…...
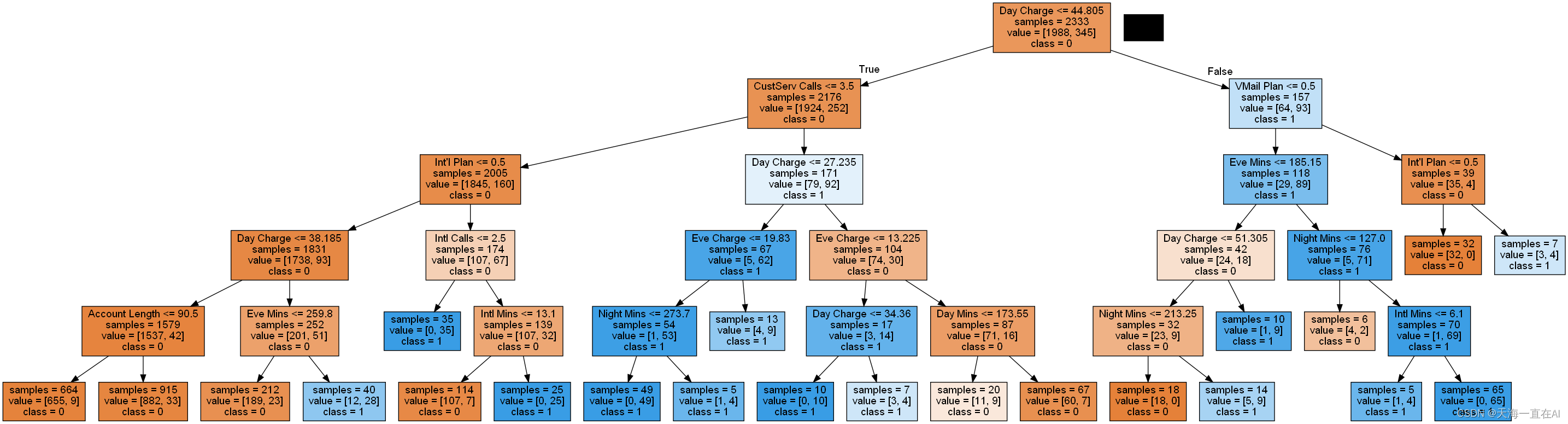
机器学习技术(十)——决策树算法实操,基于运营商过往数据对用户离网情况进行预测
机器学习技术(十)——决策树算法实操 文章目录 机器学习技术(十)——决策树算法实操一、引言二、数据集介绍三、导入相关依赖库四、读取并查看数据1、读取数据2、查看数据 五、数据预处理1、选择数据2、数据转码 六、建模与参数优…...
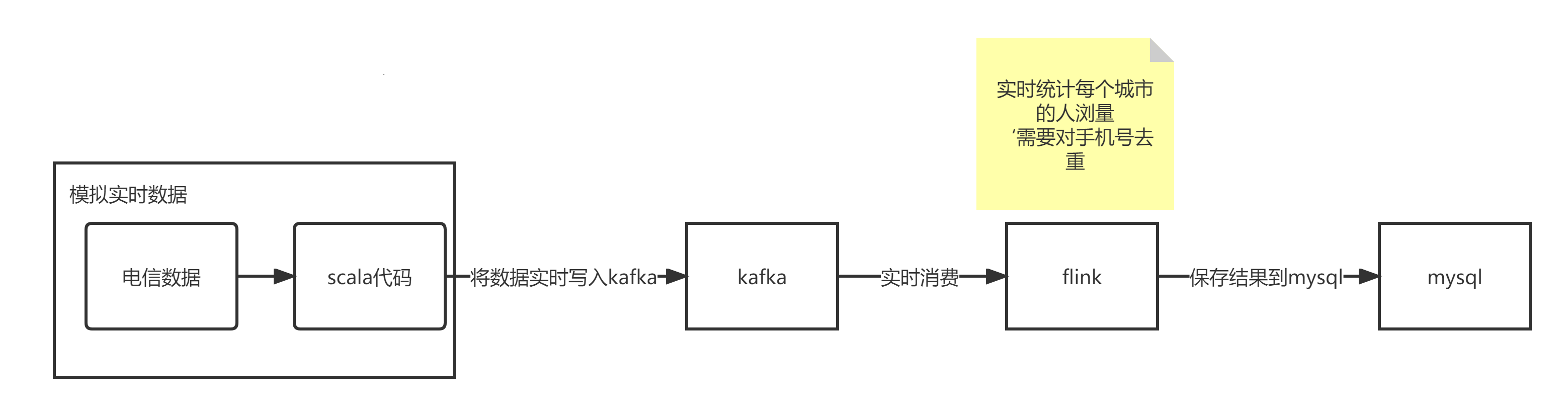
大数据之-kafka学习笔记
Kafka Kafka 是一个分布式的基于发布/订阅模式的消息队列(Message Queue),主要应用于大数据实时处理领域。 Kafka可以用作Flink应用程序的数据源。Flink可以轻松地从一个或多个Kafka主题中消费数据流。这意味着您可以使用Kafka来捕获和传输…...

虚幻动画系统概述
本文主要整理一下高层次的概述,方便后续查阅 1.动画流程 DCC产出动画文件 -> UE动画导入 -> 动画蓝图驱动(类似unity的动画状态机) ->动画后处理蓝图驱动(例如修型骨,骨骼矫正等后期处理) 2.动…...

什么是集成测试?集成测试方法有哪些?
1、基本概念: 将软件集成起来后进行测试。集成测试又叫子系统测试、组装测试、部件测试等。集成测试主要是针对软件高层设计进行测试,一般来说是以模块和子系统为单位进行测试。 2、集成测试包含的层次: 1. 模块内的集成,主要是…...

elementUI中的el-form常用校验规则
elementUI中的el-form常用校验规则: 校验使用方式: rules: {name: [{ required: true, message: 请输入活动名称, trigger: blur },{ min: 3, max: 5, message: 长度在 3 到 5 个字符, trigger: blur }],region: [{ required: true, message: 请选择活动区域, trig…...

蓝桥杯打卡Day9
文章目录 直角三角形最长平衡串 一、直角三角形IO链接 本题思路:本题就是利用欧几里得距离求解即可。 #include <bits/stdc.h>int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T;std::cin>>T;while(T--){int x…...
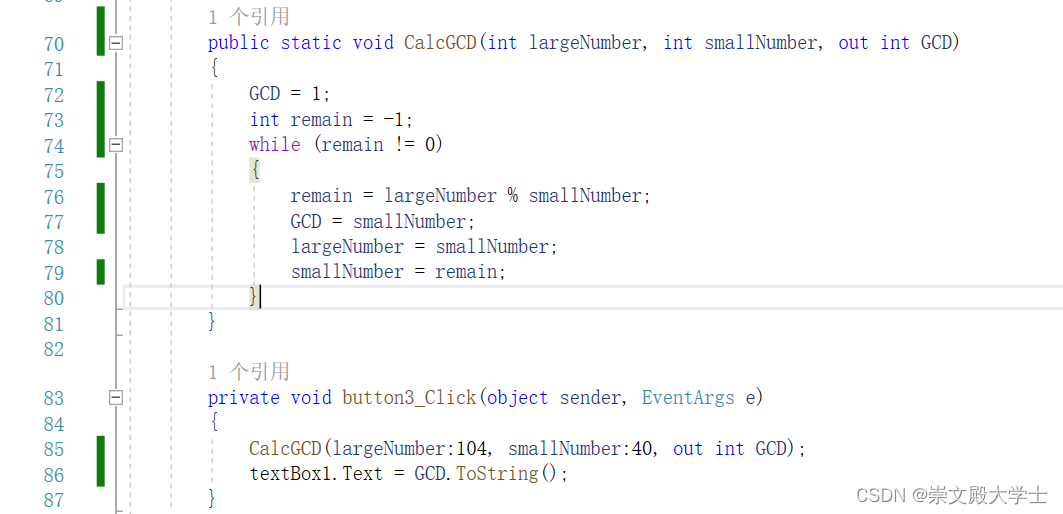
C# 辗转相除法求最大公约数
辗转相除法求最大公约数 public static void CalcGCD(int largeNumber, int smallNumber, out int GCD){GCD 1;int remain -1;while (remain ! 0){remain largeNumber % smallNumber;GCD smallNumber;largeNumber smallNumber;smallNumber remain;}}...
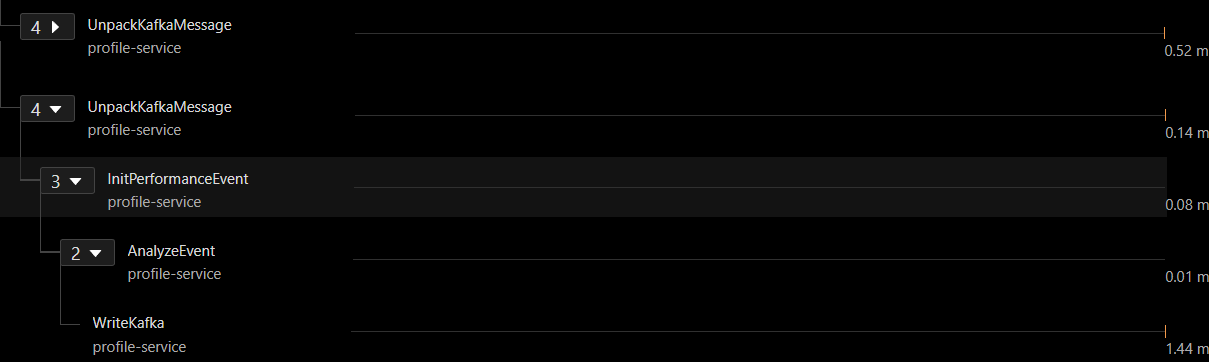
腾讯mini项目-【指标监控服务重构】2023-08-03
今日已办 a,b两组的trace放到一个分支里 可以看到先前的没看到的 profile trace 的耗时,是由于时间跨度较长,没有滑动到 trace 末尾 明日待办 组长会议汇报项目进度和问题...

redis缓存穿透、击穿、雪崩介绍
缓存穿透 概念 缓存穿透指某一特定时间批量请求打进来并访问了缓存和数据库都没有的key,此时会直接穿透缓存直达数据库,从而造成数据库瞬时压力倍增导致响应速度下降甚至崩溃的风险; 解决方案 一、通过布隆过滤器解决 原理:将…...

Redis 基础总结
1、NoSQL概述 1.1 数据库分类 目前数据库分:关系型数据库与非关系型数据库 常用的关系型数据库: Oracle,MySQL,SqlServer,DB2 常用的非关系数据库:Redis,MongoDB,ElasticSearch&…...
)
基于nginx的tomcat负载均衡和集群(超简单)
今天看到"基于apache的tomcat负载均衡和集群配置 "这篇文章成为javaEye热点。 略看了一下,感觉太复杂,要配置的东西太多,因此在这里写出一种更简洁的方法。 要集群tomcat主要是解决SESSION共享的问题,因此我利用memcac…...
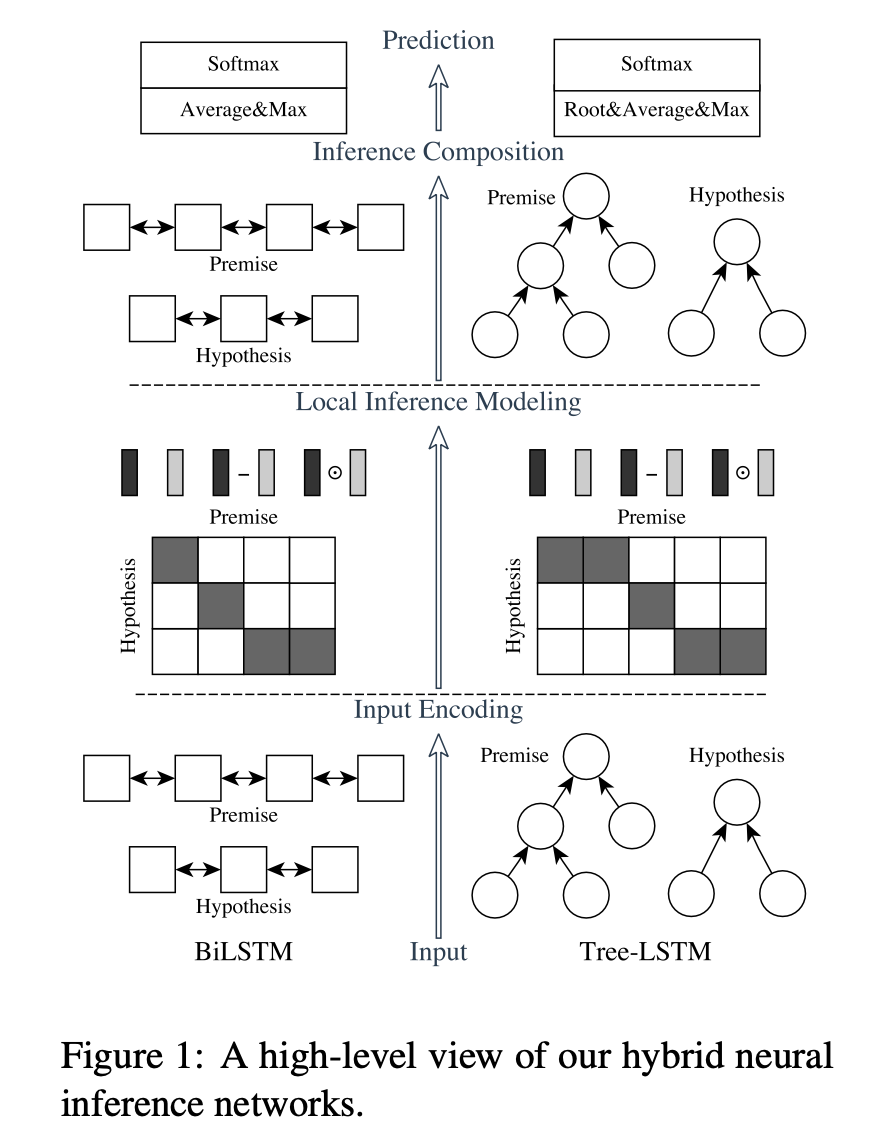
ESIM实战文本匹配
引言 今天我们来实现ESIM文本匹配,这是一个典型的交互型文本匹配方式,也是近期第一个测试集准确率超过80%的模型。 我们来看下是如何实现的。 模型架构 我们主要实现左边的ESIM网络。 从下往上看,分别是 输入编码层(Input Ecoding) 对前…...
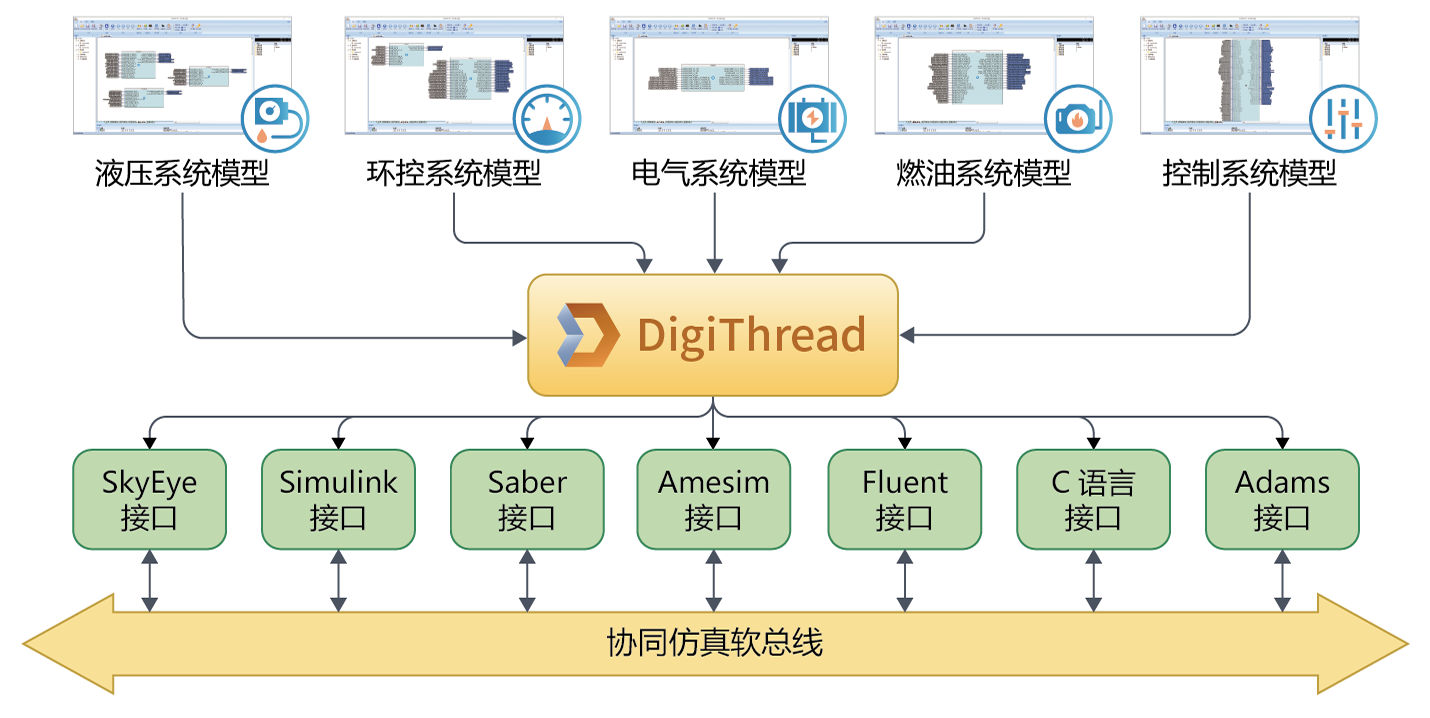
基于虚拟仿真技术的汽车燃油泵控制
在当前激烈的竞争环境下,汽车行业正在加速产业和技术更迭,整车厂对大型ECU嵌入式控制系统和软件的需求迫在眉睫。 然而,复杂而庞大的汽车系统往往由多个物理系统组成,系统所对应的模型都需要在不同的领域实现:发动机、…...

angular:HtmlElement的子节点有Shadow dom时奇怪的现象
描述: 这样写时,会自动跳过shadow dom节点的遍历 const cloneElement this.contentElement.cloneNode(true) as HTMLElement; for(let childNodeIndex 0; childNodeIndex < cloneElement.childNodes.length; childNodeIndex) {element.appendChild…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
