解决IntelliJ IDEA执行maven打包,执行java -jar命令提示jar中没有主清单属性
问题场景
IDEA执行
mvn clean package -DskipTest=true命令或者借助工具的Maven菜单进行打包操作,然后执行java -jar app.jar命令后,提示jar中没有主清单属性
D:\WorkSpace\demo\target>java -jar demo-SNAPSHOT.jar
demo-SNAPSHOT.jar中没有主清单属性
原因分析
这个错误通常是由于生成的JAR文件缺少一个主清单属性引起的。在使用
java -jar命令运行JAR文件时,JVM需要查找JAR文件中包含Main-Class属性的清单文件。如果没有找到这个属性,就会出现该错误。
验证分析
打开Jar包,查看其构建的jar目录,可以看到有一个MANIFEST.MF文件。该文件就是jar运行时要查找的清单目录,其中主清单数据,就是要运行的主类,即main函数入口所在的类
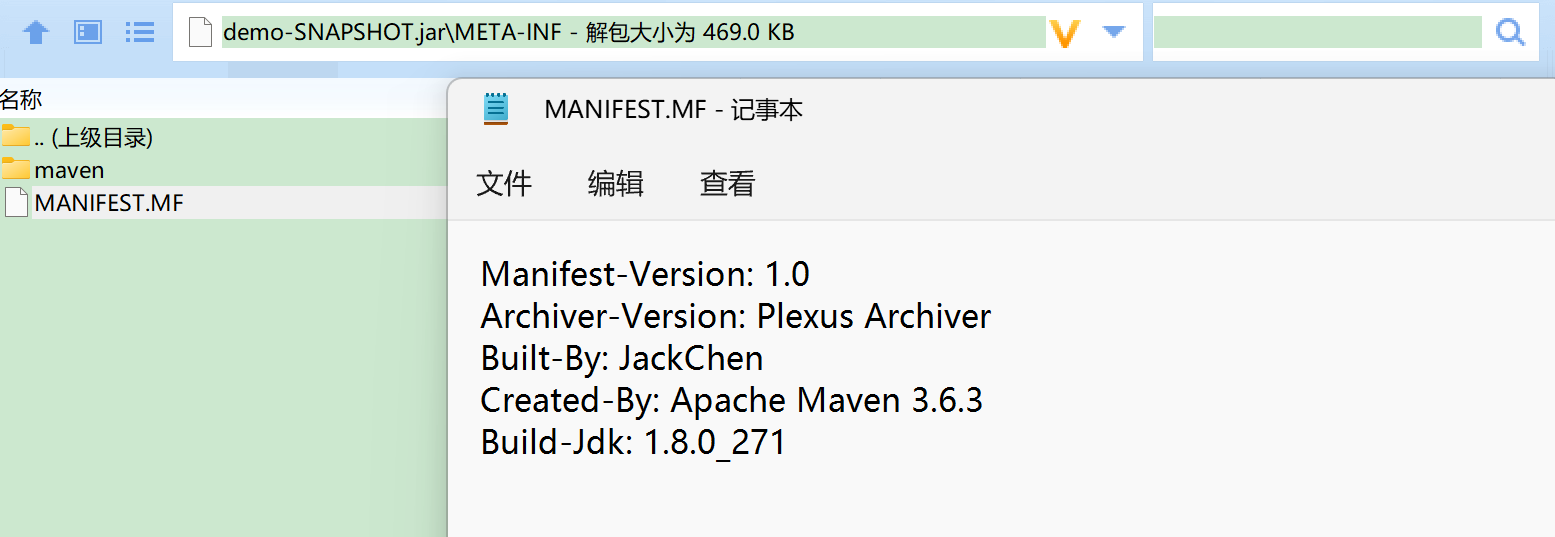
正常情况下,该清单文件内会有一个:
Main-Class:cn.ybzy.demo.mainDemo
解决方案
添加Main-Class
手动创建一个包含
Main-Class清单属性的MANIFEST.MF文件,然后将其添加到JAR文件中
打开Jar包,在MANIFEST.MF文件中,添加Main-Class主类
Main-Class:cn.ybzy.demo.mainDemo
使用插件
1.使用maven-jar-plugin插件
在pom.xml文件中使用
maven-jar-plugin插件,并在其中指定了<mainClass>属性。
<build><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-jar-plugin</artifactId><version>3.2.0</version><configuration><archive><manifest><addClasspath>true</addClasspath><mainClass>com.example.MainClass</mainClass></manifest></archive></configuration></plugin></plugins>
</build>
2.使用maven-shade-plugin插件
<build><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-shade-plugin</artifactId><version>3.2.4</version><executions><execution><phase>package</phase><goals><goal>shade</goal></goals><configuration><transformers><transformer implementation="org.apache.maven.plugins.shade.resource.ManifestResourceTransformer"><mainClass>com.example.MainClass</mainClass></transformer></transformers></configuration></execution></executions></plugin></plugins></build>
相关文章:

解决IntelliJ IDEA执行maven打包,执行java -jar命令提示jar中没有主清单属性
问题场景 IDEA执行mvn clean package -DskipTesttrue命令或者借助工具的Maven菜单进行打包操作,然后执行java -jar app.jar命令后,提示jar中没有主清单属性 D:\WorkSpace\demo\target>java -jar demo-SNAPSHOT.jar demo-SNAPSHOT.jar中没有主清单属性…...

Python--文件和异常
目录 1、读取文件 1.1 读取文件的全部内容 1.2 相对路径和绝对路径 1.3 访问文件中的各行 1.4 使用文件中的内容 1.5 包含100万位的大型文件 1.6 圆周率中的生日 2、写入文件 2.1 写入一行 2.2 写入多行 3、异常 3.1 处理ZeroDivisionError 异常 3.2 使用try-exce…...

IDEFICS 简介: 最先进视觉语言模型的开源复现
我们很高兴发布 IDEFICS ( Image-aware Decoder Enhanced la Flamingo with Ininterleaved Cross-attention S ) 这一开放视觉语言模型。IDEFICS 基于 Flamingo,Flamingo 作为最先进的视觉语言模型,最初由 DeepMind 开发,但目前尚未公开发布…...

玩转Mysql系列 - 第20篇:异常捕获及处理详解
这是Mysql系列第20篇。 环境:mysql5.7.25,cmd命令中进行演示。 代码中被[]包含的表示可选,|符号分开的表示可选其一。 需求背景 我们在写存储过程的时候,可能会出现下列一些情况: 插入的数据违反唯一约束ÿ…...

一些工具类
1、字符串处理工具类 1.1、StrUtils package com.study.java8.util;/*** Classname:StrUtils* Description:字符串工具类* Date:2023/9/9 9:37* Author:jsz15*/import org.apache.commons.lang.text.StrBuilder; import org.apa…...

20230916后台面经整理
1.面对抢优惠券这样的高负载场景,你从架构、负载均衡等方面说一下你的设计? 答了参考Nginx进行负载均衡,然后在每台服务器怎么怎么弄(架构每一层怎么设计) 参考https://toutiao.io/posts/6z3uu2m/preview,h…...
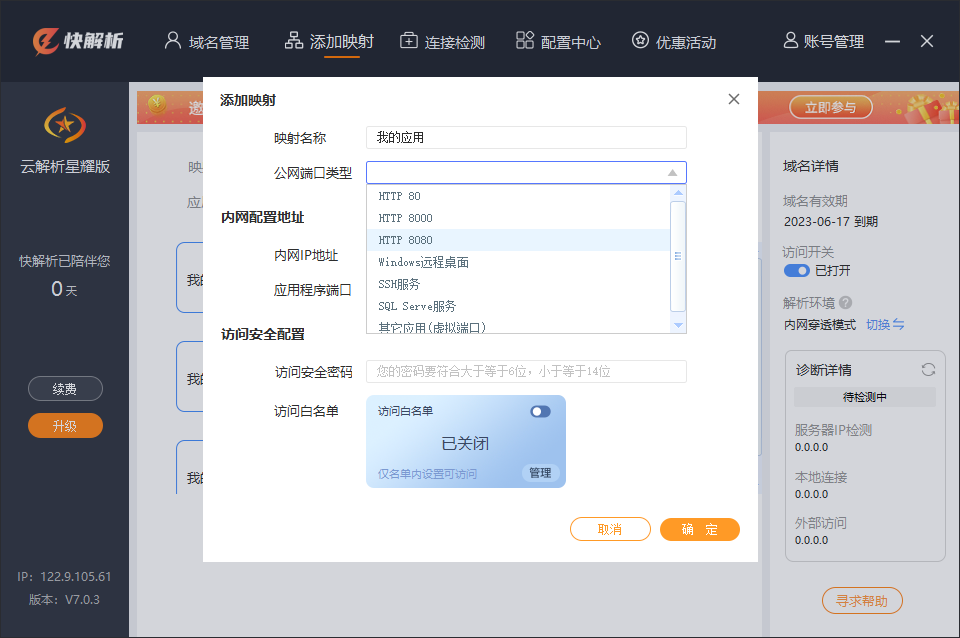
如何通过快解析测试接口内外网?本地内网ip让外网访问连接
接口调试测试是网络技术员经常工作内容之一。如在公司内部api项目webserver测试,在公司内办公室个人电脑是正常用内网IP访问连接测试的,但在外网电脑需要远程测试时需要怎么测试呢?这里提供一种内网地址让外网访问的通用方法:快解…...
用c++实现五子棋小游戏
五子棋是一款经典小游戏,今天我们就用c实现简单的五子棋小游戏 目录 用到的算法: 思路分析 定义变量 开始写代码 完整代码 结果图: 用到的算法: 合法移动的判断:isValidMove 函数通过检查指定位置是否在棋盘范…...
Android 12.0 SystemUI下拉状态栏定制化之隐藏下拉通知栏布局功能实现(二)
1.前言 在12.0的系统定制化开发中,由于从12.0开始SystemUI下拉状态栏和11.0的变化比较大,所以可以说需要从新分析相关的SystemUI的 布局,然后做分析来实现不同的功能,今天就开始实现关于隐藏SystemUI下拉状态栏中的通知栏布局系列二,去掉下拉状态栏中 通知栏部分 白色的…...
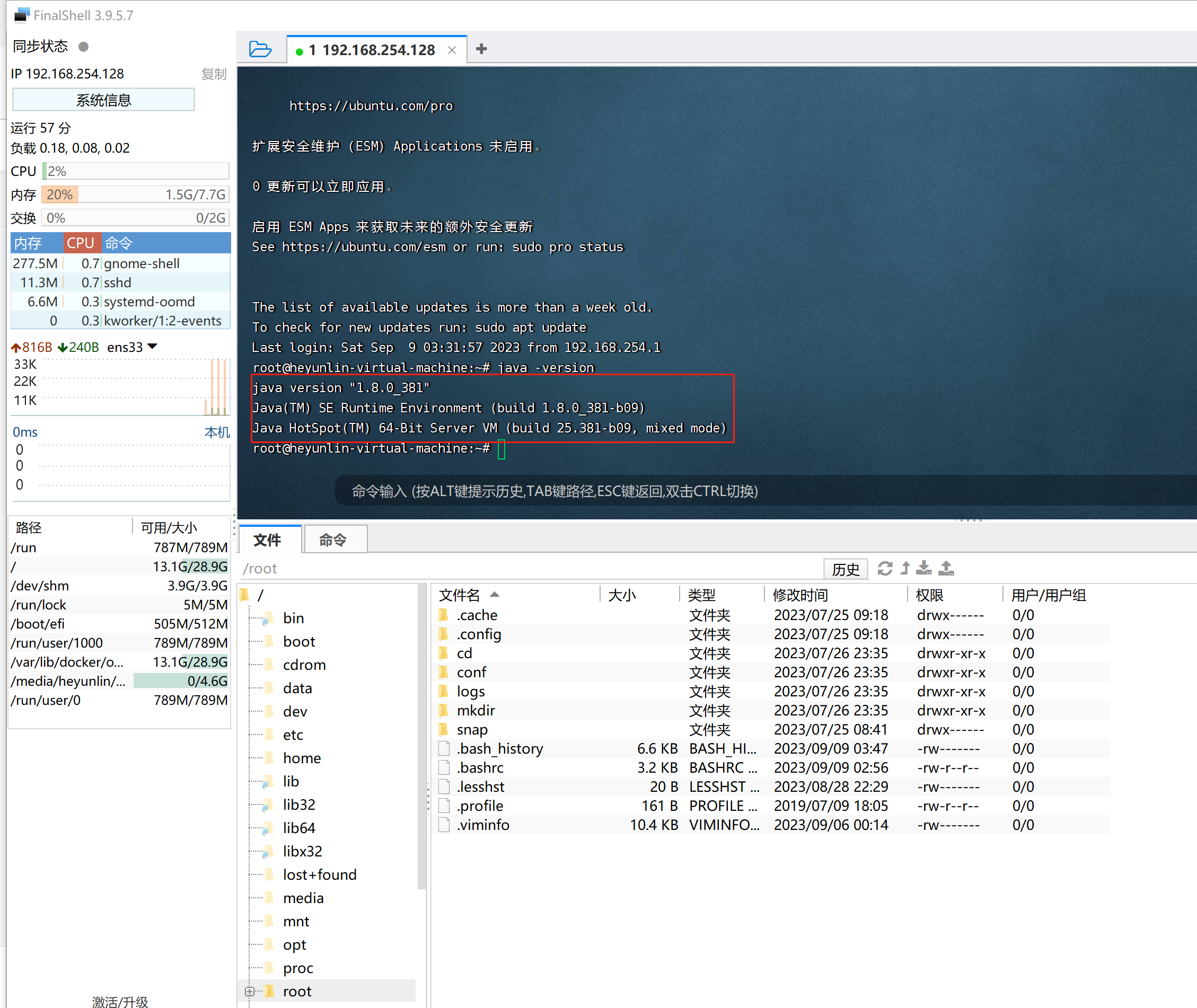
通过finalshell快速在ubuntu上安装jdk1.8
这篇文章主要介绍一下怎么通过finalshell连接ubuntu,然后在ubuntu上安装jdk1.8,让不熟悉linux操作系统的童鞋也能快速地完成安装。 目录 一、准备一台虚拟机 二、安装finalshell远程连接工具 三、获取ubuntu虚拟机的ip地址 四、通过finalshell连接u…...
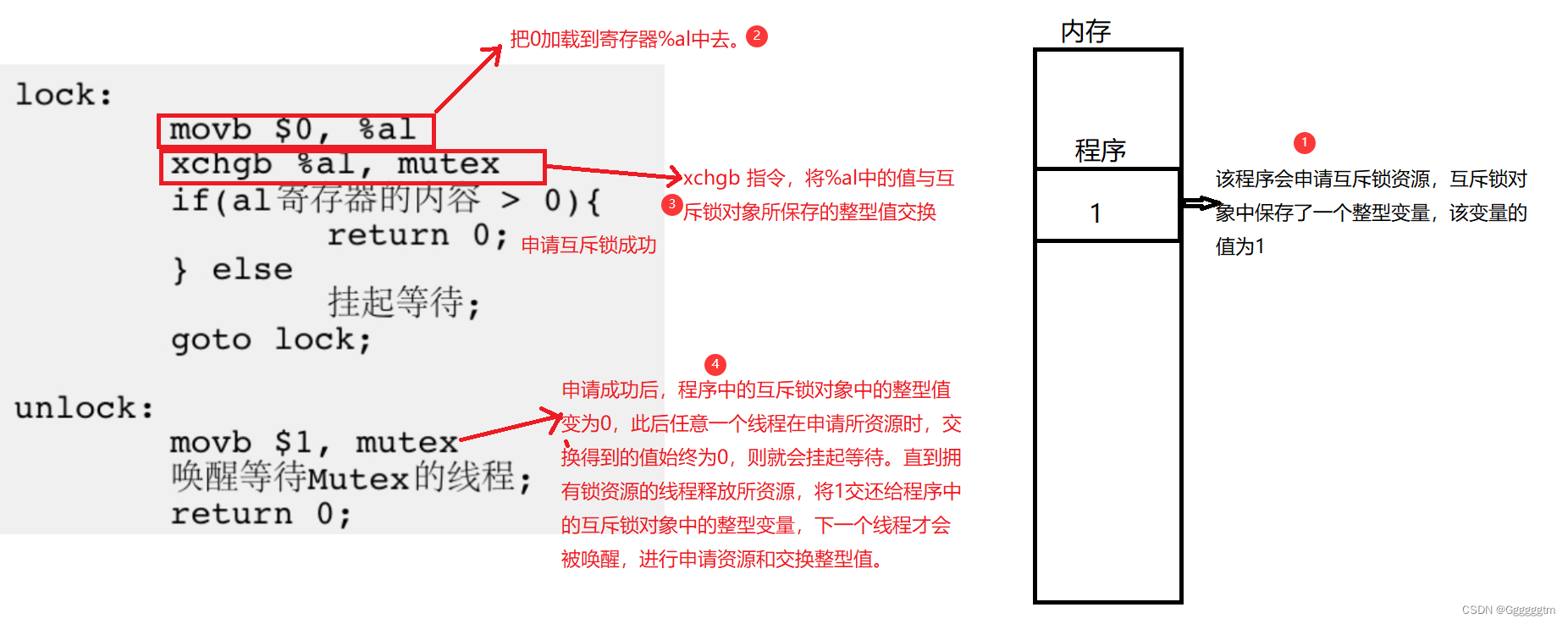
【Linux从入门到精通】多线程 | 线程互斥(互斥锁)
上篇文章我们对线程 | 线程介绍&线程控制介绍后,本篇文章将会对多线程中的线程互斥与互斥锁的概念进行详解。同时结合实际例子解释了可重入与不被重入函数、临界资源与临界区和原子性的概念。希望本篇文章会对你有所帮助。 文章目录 引入 一、重入与临界 1、1 可…...
Echarts 散点图的详细配置过程
文章目录 散点图 简介配置步骤简易示例 散点图 简介 Echarts散点图是一种常用的数据可视化图表类型,用于展示两个或多个维度的数据分布情况。散点图通过在坐标系中绘制数据点的位置来表示数据的关系。 Echarts散点图的特点如下: 二维数据展示ÿ…...
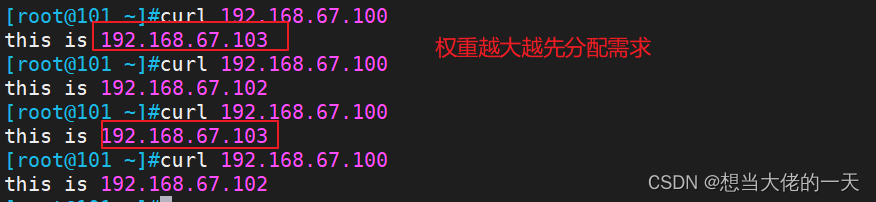
Nginx详解 五:反向代理
文章目录 1. 正向代理和反向代理1.1 正向代理概述1.1.1 什么是正向代理1.1.2 正向代理的作用1.1.3 正向代理的基本格式 1.2 反向代理概述1.2.1 什么是反向代理1.2.2 反向代理可实现的功能1.2.3 反向代理的可用模块 2. 配置反向代理2.1 反向代理配置参数2.1.1 proxy_pass2.1.2 其…...

【PDF密码】PDF文件打开之后不能打印,怎么解决?
正常的PDF文件是可以打印的,如果PDF文件打开之后发现文件不能打印,我们需要先查看一下自己的打印机是否能够正常运行,如果打印机是正常的,我们再查看一下,文件中的打印功能按钮是否是灰色的状态。 如果PDF中的大多数功…...
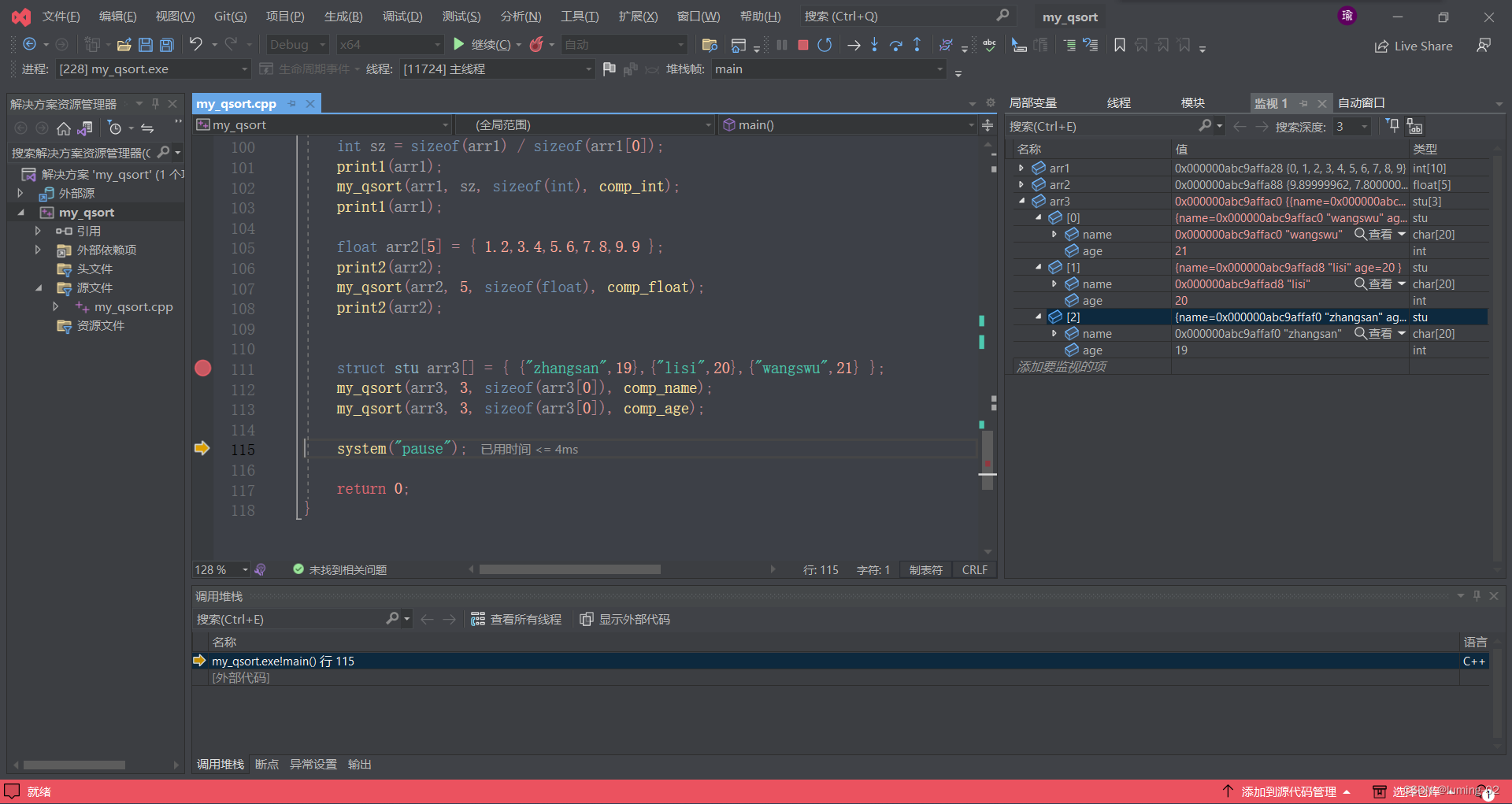
深入解析 qsort 函数(下),用冒泡排序模拟实现 qsort 函数
前言:对于库函数有适当了解的朋友们,对于 qsort 函数想必是有认知的,因为他可以对任意数据类型进行排序的功能属实是有点厉害的,本次分享,笔者就给大家带来 qsort 函数的全面的解读 本次知识的分享笔者分为上下俩卷文章…...

Azure + React + ASP.NET Core 项目笔记一:项目环境搭建(二)
有意义的标题 pnpm 安装umi4 脚手架搭建打包语句变更Visual Studio调试Azure 设置变更发布 pnpm 安装 参考官网,或者直接使用npm安装 npm install -g pnpmumi4 脚手架搭建 我这里用的umi4,官网已附上 这里需要把clientapp清空,之后 cd Cl…...

Vmware通过VMware tools设置共享文件夹
步骤说明: 先安装VMware tools,再设置共享文件夹即可。 写在前面: 刚安装虚拟机时,窗口可能显得太小,这是窗口分辨率没有调整导致的。 点击设置->显示->分辨率调整即可 一、安装VMware tools 1.1 点击虚拟机…...
)
RPA机器人流程自动化专题培训大纲 (针对大学生的版本)
一、课程简介 RPA机器人流程自动化是一种新兴的技术,它通过软件机器人模拟人类操作计算机完成重复性任务,从而实现业务流程的自动化。本课程旨在介绍RPA机器人流程自动化的基本概念、原理和应用,并通过实践案例演示如何应用RPA机器人流程自动…...

数据在内存中的存储——练习4
题目: int main() {char a[1000];int i;for(i0; i<1000; i){a[i] -1-i;}printf("%d",strlen(a));return 0; }思路分析: 已知条件: 通过循环遍历,我们得到的结果是 -1、-2、-3、-4等等。这些是数组内部的存储的元…...

Python 06 之面向对象基础
😀前言 在日常编程和软件开发中,我们通常会遇到各种各样的问题,其中很多问题都可以通过面向对象的程序设计方法来解决。面向对象编程不仅可以使代码更加组织化和系统化,而且还可以提高代码的重用性和可维护性。 . 在本教程中&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
