线性dp,优化,272. 最长公共上升子序列
272. 最长公共上升子序列 - AcWing题库
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。
小沐沐说,对于两个数列 A 和 B,如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个数列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过,只要告诉奶牛它的长度就可以了。
数列 A 和 B 的长度均不超过 3000。
输入格式
第一行包含一个整数 N,表示数列 A,B 的长度。
第二行包含 N 个整数,表示数列 A。
第三行包含 N 个整数,表示数列 B。
输出格式
输出一个整数,表示最长公共上升子序列的长度。
数据范围
1≤N≤3000,序列中的数字均不超过 231−1。
输入样例:
4
2 2 1 3
2 1 2 3
输出样例:
2解析
(DP,线性DP,前缀和) O(n2)
这道题目是AcWing 895. 最长上升子序列和AcWing 897. 最长公共子序列的结合版,在状态表示和状态计算上都是融合了这两道题目的方法。状态表示:
f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合;
f[i][j]的值等于该集合的子序列中长度的最大值;
状态计算(对应集合划分):首先依据公共子序列中是否包含a[i],将f[i][j]所代表的集合划分成两个不重不漏的子集:
不包含a[i]的子集,最大值是f[i - 1][j];
包含a[i]的子集,将这个子集继续划分,依据是子序列的倒数第二个元素在b[]中是哪个数:
子序列只包含b[j]一个数,长度是1;
子序列的倒数第二个数是b[1]的集合,最大长度是f[i - 1][1] + 1;
…
子序列的倒数第二个数是b[j - 1]的集合,最大长度是f[i - 1][j - 1] + 1;
如果直接按上述思路实现,需要三重循环:作者:yxc
链接:https://www.acwing.com/solution/content/4955/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
for (int i = 1; i <= n; i ++ )
{for (int j = 1; j <= n; j ++ ){f[i][j] = f[i - 1][j];if (a[i] == b[j]){int maxv = 1;for (int k = 1; k < j; k ++ )if (a[i] > b[k])maxv = max(maxv, f[i - 1][k] + 1);f[i][j] = max(f[i][j], maxv);}}
}作者:yxc
链接:https://www.acwing.com/solution/content/4955/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。优化后将三重循环压缩成两成层循环
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>using namespace std;
typedef long long LL;
const int N = 3e3 + 5;
int n;
int a[N], b[N],f[N][N];int main() {scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);}for (int i = 1; i <= n; i++) {scanf("%d", &b[i]);}for (int i = 1; i <= n; i++) {int maxv = 1;for (int j = 1; j <= n; j++) {f[i][j] = f[i - 1][j];if (a[i] == b[j]) {f[i][j] = max(f[i][j], maxv);}if (a[i] > b[j])maxv = max(maxv, f[i - 1][j]+1);}}int ans = 0;for (int i = 1; i <= n; i++) {ans = max(ans, f[n][i]);}cout << ans << endl;return 0;
}相关文章:

线性dp,优化,272. 最长公共上升子序列
272. 最长公共上升子序列 - AcWing题库 熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。 小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。 小沐沐说,对于两个数列 A 和 B&…...
基于Java+SpringBoot+Vue+uniapp点餐小程序(包含协同过滤算法和会员系统,强烈推荐!)
校园点餐小程序 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 系统功能结构设计4.2 主要功能描述 五…...
)
ActiveMQ面试题(二)
文章目录 前言一、死信队列二、ActiveMQ 中的消息重发时间间隔和重发次数吗?总结 前言 死信队列ActiveMQ 中的消息重发时间间隔和重发次数吗? 一、死信队列 如果你想在消息处理失败后,不被服务器删除,还能被其他消费者处理或重试…...
)
解决Oracle SQL语句性能问题——SQL语句改写(in、not in、exists及not exists)
8. in改为join in为Oracle数据库支持的条件语法,该语法会使得代码看起来思路清晰,逻辑分明。该语法有时也会导致SQL语句产生次优的执行计划,而导致SQL语句的性能问题。因此,为了解决相关SQL语句的性能问题,有时我们需要通过join来改写和消除in,具体改写方法如下所示。 …...
列表对象复制属性到另一个列表对象 从List<Object>另一个List<Object>
目录 事件起因环境和工具解决办法结束语 事件起因 在写一个市级的项目时,遇到了一个问题,这个项目涉及的数据内容非常大,光是数据库文件的大小就已经达到了12G,数据的规模大致是在百万级的,光是我这次参与处理的数据就…...

Python基本情况
Python(发音:/ˈpaɪθən/ )是一种强大的编程语言,它简单易学,提供众多高级的数据结构,让我们可以面向对象进行编程。Python 的语法优雅,由于是一个解释性语言,更贴近人类自然语言&…...

【精华】AI Agent:大模型改变世界的“钥匙”
文章目录 1.Auto-GPT2.BabyAGI3.AgentGPT4.GodMode5.AI Town6.ChatDev 当前大模型的本质是大语言模型(Large Language Model, LLM)。相较于传统的自然语言处理模型,LLM通过无监督训练,从大量文本数据中学习自然语言的模式和结构&a…...
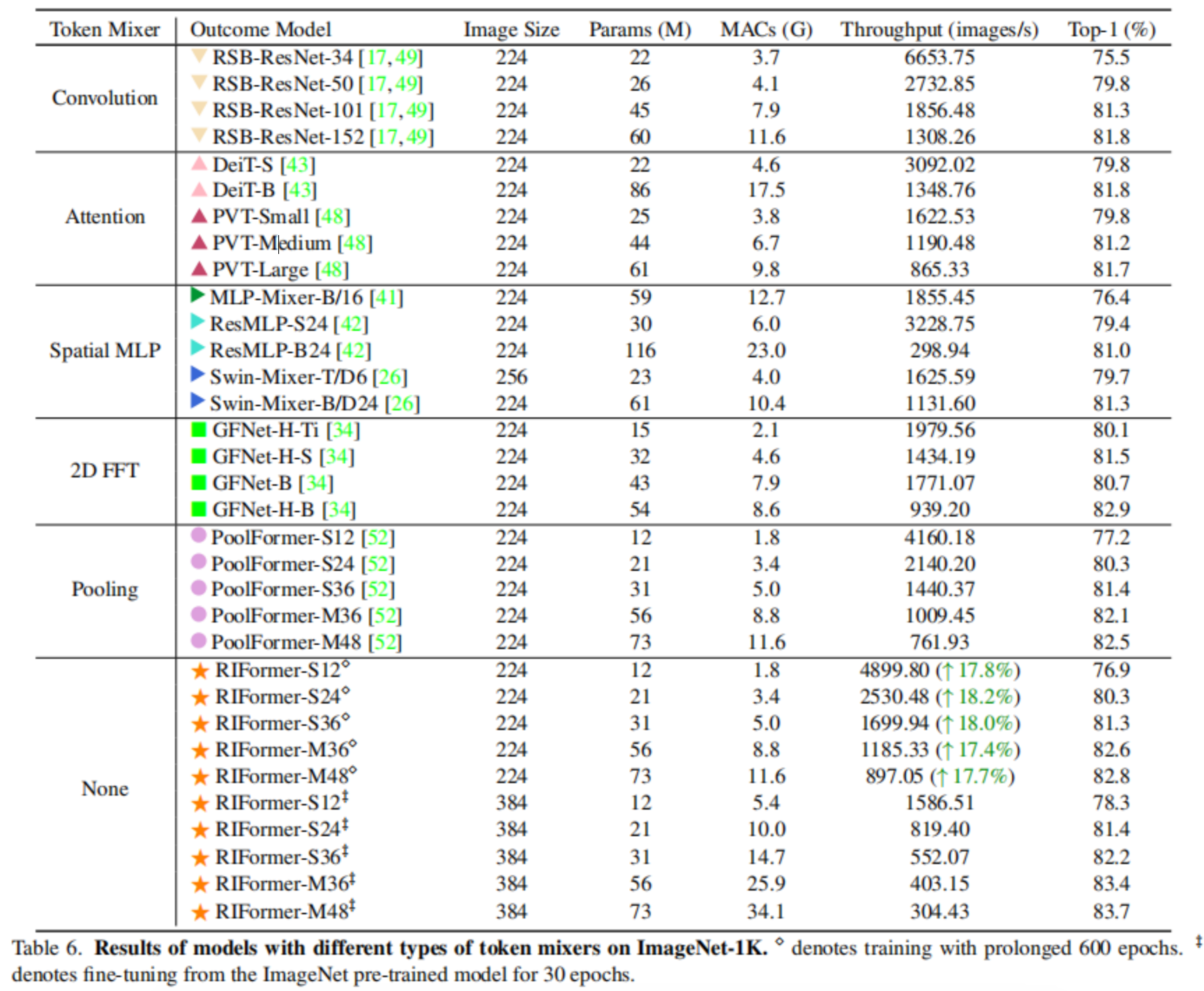
CVPR2023 RIFormer, 无需TokenMixer也能达成SOTA性能的极简ViT架构
编辑 | Happy 首发 | AIWalker 链接 | https://mp.weixin.qq.com/s/l3US8Dsd0yNC19o7B1ZBgw project, paper, code Token Mixer是ViT骨干非常重要的组成成分,它用于对不同空域位置信息进行自适应聚合,但常规的自注意力往往存在高计算复杂度与高延迟问题。…...

瑞萨MCU入门教程(非常详细的瑞萨单片机入门教程)
瑞萨MCU零基础入门系列教程 前言 得益于瑞萨强大的MCU、强大的软件开发工具(e studio),也得益于瑞萨和RA生态工作室提供的支持,我们团队编写了《ARM嵌入式系统中面向对象的模块编程方法》,全书37章,将近500页: 讲解面向对象编程…...

【Java】采用 Tabula 技术对 PDF 文件内表格进行数据提取
某天项目组来了个需求说需要提取 PDF 文件中数据作为数据沉淀使用,这是因为第三方系统不提供数据接口所以只能够出此下策。 就据我所知,PDF 文件内数据提取目前有 3 种解决方案: 第一种,资金足够的话可以直接通过人工智能对 PDF…...
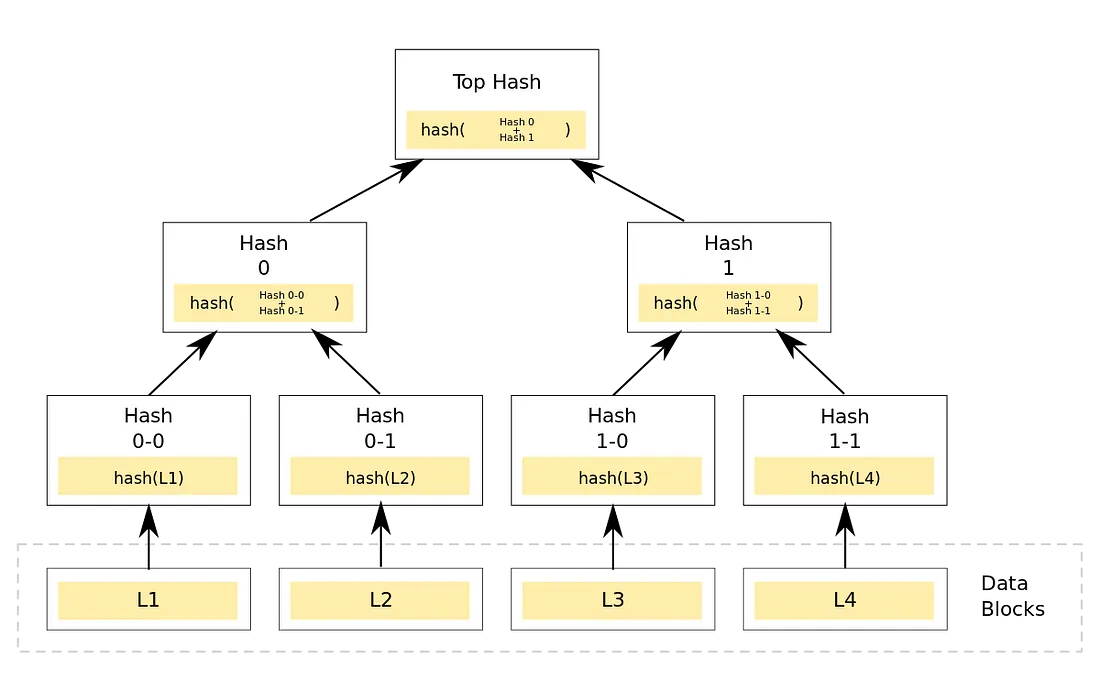
完全保密的以太坊交易:Aztec网络的隐私架构
1. 引言 Aztec为隐私优先的以太坊zkRollup:即其为具有完全隐私保护的L2。 为了理解私有交易的范式变化性质,以及为什么将隐私直接构建到网络架构中很重要,必须首先讨论为什么以太坊不是私有的。 2. 以太坊:公有链 以太坊为具有…...

初识Java 9-1 内部类
目录 创建内部类 到外部类的链接 使用.this和.new 内部类和向上转型 在方法和作用域中的内部类 匿名内部类 嵌套类 接口中的类 从多嵌套的内部类中访问外部人员 本笔记参考自: 《On Java 中文版》 定义在另一个类中的类称为内部类。利用内部类,…...
)
合宙Air724UG LuatOS-Air LVGL API控件-屏幕横屏竖屏切换(Rotation)
屏幕横屏竖屏切换(Rotation) lvgl.disp_set_rotation(nil, lvgl.DISP_ROT_angle) 屏幕横屏竖屏切换显示,core版本号要>3202参数 参数类型释义取值nil无意义nilangle显示角度0,90,270,360 返回值nil 例子 lvgl.init()- -初始化 lvgl.disp_set_rotation(nil,…...

在Unity中,Instantiate函数用于在场景中创建一个新的游戏对象实例
在Unity中,Instantiate函数用于在场景中创建一个新的游戏对象实例。它的语法如下所示: public static Object Instantiate(Object original, Vector3 position, Quaternion rotation); original:要实例化的原始游戏对象。position࿱…...

解决 tesserocr报错 Failed to init API, possibly an invalid tessdata path : ./
问题描述 我们在初次使用tesserocr库的时候,可能会报以下错误: RuntimeError: Failed to init API, possibly an invalid tessdata path: ./ 这是因为我们在使用 conda 创建的环境中找不到"tessdata"这个文件夹。 解决办法 这时候把Tessera…...

使用Python CV2融合人脸到新图片--优化版
优化说明 上一版本人脸跟奥特曼图片合并后边界感很严重,于是查找资料发现CV2还有一个泊松函数很适合融合图像。具体代码如下: import numpy as np import cv2usrFilePath "newpic22.jpg" atmFilePath "atm2.jpg" src cv2.imrea…...

Python分享之对象的属性
Python一切皆对象(object),每个对象都可能有多个属性(attribute)。Python的属性有一套统一的管理方案。 属性的__dict__系统 对象的属性可能来自于其类定义,叫做类属性(class attribute)。类属性可能来自类定义自身,也可能根据类定义继承来的…...

编程参考 - std::exchange和std::swap的区别
这两个功能是C standard library中的Standard template library中的一部分。容易混淆,我们来看下它们的区别。 exchange: 这个函数是一个返回原先值的set函数。 std::exchange is a setter returning the old value. int z std::exchange(x, y); Af…...

Sentinel整合RestTemplate
resttemplate开启sentinel保护配置resttemplate.sentinel.enabledtrue配置sentinel-dashboard地址spring.cloud.sentinel.transport.dashboardlocalhost:8858\ spring.cloud.sentinel.transport.dashboard.port8739 实例化RestTemplate并加入SentinelRestTemplate注解Configura…...
)
微前端学习(下)
一、课程目标 qiankun 整体运行流程微前端实现方案二、课程大纲 qiankun 整体流程微前端方案实现DIY微前端核心能力1、微前端方案实现 基于 iframe 完全隔离的方案、使用纯的Web Components构建应用EMP基于webpack module federationqiankun、icestark 自己实现JS以及样式隔离2…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
