【数据结构】C++实现二叉搜索树
二叉搜索树的概念
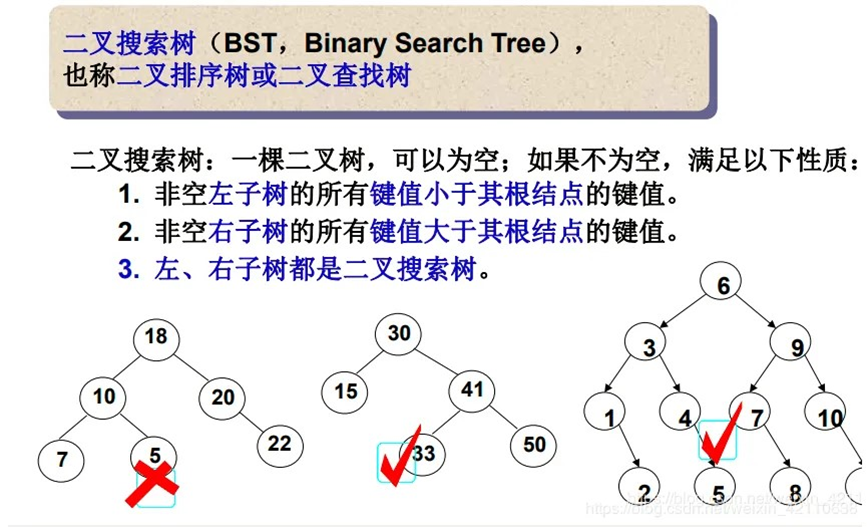
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。
- 若它的右子树不为空,则右子树上所有结点的值都大于根结点的值。
- 它的左右子树也分别是二叉搜索树。
由于二叉搜索树中,每个结点左子树上所有结点的值都小于该结点的值,右子树上所有结点的值都大于该结点的值,因此对二叉搜索树进行中序遍历后,得到的是升序序列也就不难理解了。
二叉搜索树的操作
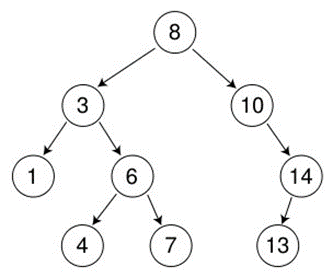
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到空,还没找到,这个值不存在。
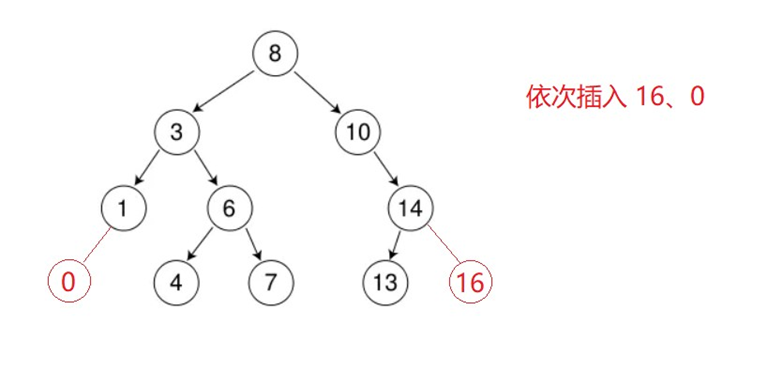
二叉搜索树的插入
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
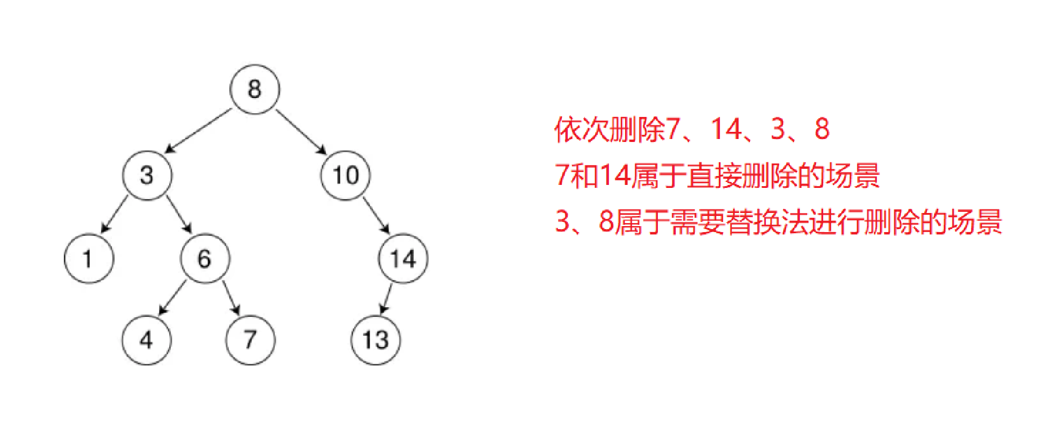
二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d:在被删除的结点的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题–替换法删除
二叉搜索树的实现
结点类
要实现二叉搜索树,我们首先需要实现一个结点类:
- 结点类当中包含三个成员变量:结点值、左指针、右指针。
- 结点类当中只需实现一个构造函数即可,用于构造指定结点值的结点。
template<class K>
// 二叉树的结构
struct BSTreeNode {BSTreeNode<K> *_left; //左孩子指针BSTreeNode<K> *_right;//右孩子指针K _key; //结点值//构造函数BSTreeNode(const K &key = 0): _left(nullptr), _right(nullptr), _key(key) {}
};
BSTree类
#pragma once
#include <iostream>
using namespace std;template<class K>
class BSTree {typedef BSTreeNode<K> Node;public:BSTree() = default;//指定强制生成默认构造//默认构造BSTree();//拷贝构造BSTree(const BSTree<K> &t);//赋值重载BSTree<K> &operator=(BSTree<K> t);//析构函数~BSTree();//插入key值bool Insert(const K &key);//查找key值bool Find(const K &key);//删除key值bool Erase(const K &key);//递归查找 bool FindR(const K &key);//递归插入bool InsertR(const K &key);//递归删除bool EraseR(const K &key);//中序遍历void InOrder();
private:Node *_root = nullptr;// 二叉搜索树的根
};
构造函数
//构造一个空树
BSTree(): _root(nullptr) {
}
拷贝构造函数
拷贝构造函数也并不难,拷贝一棵和所给二叉搜索树相同的树即可。
Node *Copy(Node *root) {if (root == nullptr) {return nullptr;}//前序遍历copy树Node *newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;
}//构造树的深拷贝
BSTree(const BSTree<K> &t) {_root = Copy(t._root);
}
赋值运算符重载函数
对于赋值运算符重载函数,下面提供两种实现方法:
传统写法:
//传统写法
const BSTree<K> &operator=(const BSTree<K> &t) {//避免自己拷贝自己if (this != &t) {_root = Copy(t._root);}return *this;//为了支持连续赋值
}
现代写法:
//现代写法
BSTree<K> &operator=(BSTree<K> t) {swap(_root, t._root);return *this;
}
赋值运算符重载函数的现代写法非常精辟,函数在接收右值时并没有使用引用进行接收,因为这样可以间接调用BSTree的拷贝构造函数完成拷贝构造。我们只需将这个拷贝构造出来的对象的二叉搜索树与this对象的二叉搜索树进行交换,就相当于完成了赋值操作,而拷贝构造出来的对象t会在该赋值运算符重载函数调用结束时自动析构。
注意:两种方法都是深拷贝,效率并没有什么区别
析构函数
析构函数完成对象中二叉搜索树结点的释放,注意释放时采用后序释放,当二叉搜索树中的结点被释放完后,将对象当中指向二叉搜索树的指针及时置空即可。
void Destroy(Node *&root) {if (root == nullptr) {return;}//后序遍历析构Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;
}//析构函数
~BSTree() {Destroy(_root);
}
查找函数
根据二叉搜索树的特性,我们在二叉搜索树当中查找指定值的结点的方式如下:
- 若树为空树,则查找失败,返回nullptr。
- 若key值小于当前结点的值,则应该在该结点的左子树当中进行查找。
- 若key值大于当前结点的值,则应该在该结点的右子树当中进行查找。
- 若key值等于当前结点的值,则查找成功,返回对应结点的地址。
非递归实现
// 查找
bool Find(const K &key) {Node *cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;} else if (key < cur->_key) {cur = cur->_left;} else {return true;}}return false;
}
递归实现
bool _FindR(Node *root, const K &key) {if (root == nullptr) {return false;}if (root->_key == key) {return true;}if (key > root->_key) {return _FindR(root->_right, key);} else {return _FindR(root->_left, key);}
}bool FindR(const K &key) {return _FindR(_root, key);
}
插入函数
根据二叉搜索树的性质,其插入操作非常简单:
如果是空树,则直接将插入结点作为二叉搜索树的根结点。
如果不是空树,则按照二叉搜索树的性质进行结点的插入。
若不是空树,插入结点的具体操作如下:
- 若待插入结点的值小于根结点的值,则需要将结点插入到左子树当中。
- 若待插入结点的值大于根结点的值,则需要将结点插入到右子树当中。
- 若待插入结点的值等于根结点的值,则插入结点失败。
如此进行下去,直到找到与待插入结点的值相同的结点判定为插入失败,或者最终插入到某叶子结点的左右子树当中(即空树当中)。
非递归实现
使用非递归方式实现二叉搜索树的插入函数时,我们需要定义一个parent指针,该指针用于标记待插入结点的父结点。这样一来,当我们找到待插入结点的插入位置时,才能很好的将待插入结点与其父结点连接起来。
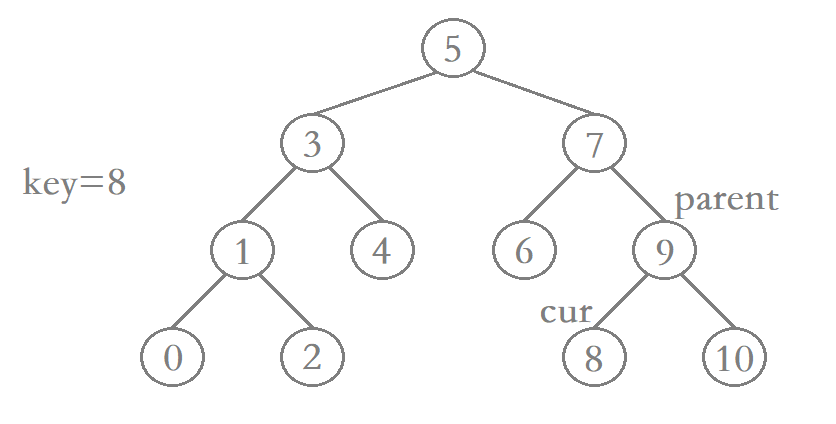
但是需要注意在连接parent和cur时,需要判断应该将cur连接到parent的左边还是右边。
bool Insert(const K &key) {// 如果根一开始就为nullptr,那么就直接构建初始的根if (_root == nullptr) {_root = new Node(key);return true;}// 如果_root不为nullptr,那么就从根开始遍历,找适合的位置Node *parent = nullptr;// parent跟着cur遍历找到合适的位置,充当插入的父亲节点Node *cur = _root;while (cur) {//key < cur->_key 需要走左子树//key > cur->_key 需要走右子树if (key < cur->_key) {parent = cur; //记录父亲结点cur = cur->_left;//走左树} else if (key > cur->_key) {parent = cur;cur = cur->_right;//走右数} else {// 如果key == cur->_key 那么就直接返回false,二叉搜索树的值不允许相同return false;}}// 找到后就开始链接cur = new Node(key);// 这里不知道cur最终走到了parent的左边还是右边,所以还要进行判断// key>parent->_key 链接右树// key<parent->_key 链接左树if (key > parent->_key) {parent->_right = cur;//右树} else if (key < parent->_key) {parent->_left = cur;//左树}return true;
}
递归实现
递归实现二叉搜索树的插入操作也是很简单的,但是要特别注意的一点就是,递归插入函数的子函数接收参数root时,必须采用引用接收,因为只有这样我们才能将二叉树当中的各个结点连接起来。
bool _InsertR(Node *&root, const K &key) {if (root == nullptr) {root = new Node(key);return root;}if (key > root->_key) {return _InsertR(root->_right, key);} else if (key < root->_key) {return _InsertR(root->_left, key);} else {return false;}
}
删除函数
二叉搜索树的删除函数是最难实现的,若是在二叉树当中没有找到待删除结点,则直接返回false表示删除失败即可,但若是找到了待删除结点,此时就有以下三种情况:
- 待删除结点的左子树为空(待删除结点的左右子树均为空包含在内)。
- 待删除结点的右子树为空。
- 待删除结点的左右子树均不为空。
下面我们分别对这三种情况进行分析处理:
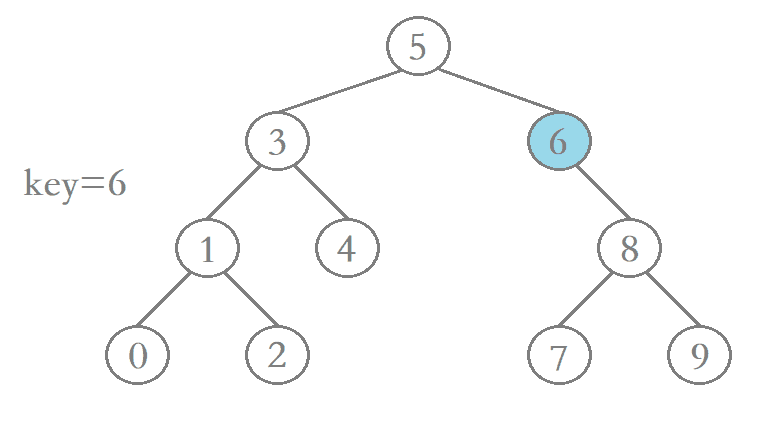
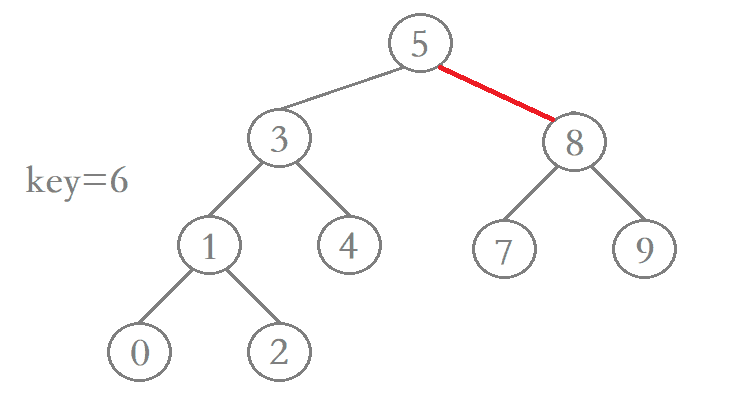
1、待删除结点的左子树为空
若待删除结点的左子树为空,那么当我们在二叉搜索树当中找到该结点后,只需先让其父结点指向该结点的右孩子结点,然后再将该结点释放便完成了该结点的删除,进行删除操作后仍保持二叉搜索树的特性。
2、待删除结点的右子树为空
若待删除结点的右子树为空,那么当我们在二叉搜索树当中找到该结点后,只需先让其父结点指向该结点的左孩子结点,然后再将该结点释放便完成了该结点的删除,进行删除操作后仍保持二叉搜索树的特性。

3、待删除结点的左右子树均不为空
若待删除结点的左右子树均不为空,那么当我们在二叉搜索树当中找到该结点后,可以使用替换法进行删除。
可以将让待删除结点左子树当中值最大的结点,或是待删除结点右子树当中值最小的结点代替待删除结点被删除(下面都以后者为例),然后将待删除结点的值改为代替其被删除的结点的值即可。而代替待删除结点被删除的结点,必然左右子树当中至少有一个为空树,因此删除该结点的方法与前面说到的情况一和情况二的方法相同。
注意只能是待删除结点左子树当中值最大的结点,或是待删除结点右子树当中值最小的结点代替待删除结点被删除,因为只有这样才能使得进行删除操作后的二叉树仍保持二叉搜索树的特性。

非递归函数
// 删除
bool Erase(const K &key) {Node *parent = nullptr;Node *cur = _root;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;} else if (key < cur->_key) {parent = cur;cur = cur->_left;} else {// 开始删除// 1.如果要删除的cur左边是nullptr,那么我们就进行判断,判断cur在parent的左子树还是右子树,// 如果是左子树,那么就由parent的left指向cur的右子树,如果是右子树,就由parent的right指向cur的右子树if (cur->_left == nullptr) {// if (parent == nullptr)if (cur == _root) {_root = cur->_right;} else {if (parent->_left == cur) {parent->_left = cur->_right;} else {parent->_right = cur->_right;}}delete cur;} else if (cur->_right == nullptr) {// 2.cur的右边为nullptr// if (parent == nullptr)if (cur == _root) {_root = cur->_left;} else {if (parent->_left == cur) {parent->_left = cur->_left;} else {parent->_right = cur->_left;}}delete cur;} else {// 都不为nullptr,替代法,用被删除的cur的左子树的最大节点,右子树的最大节点替换// 找cur右子树的最大节点Node *pminRight = cur;Node *minRight = cur->_right;// 找右子树,右子树的最小位置在右子树的左边while (minRight->_left) {pminRight = minRight;minRight = minRight->_left;}// 找到最小的值赋值给curcur->_key = minRight->_key;// pminRight->_left==minRight 那么左边已经是最小了,所以minRight的左子树肯定为空了// 那么可能minRight还有右子树,所以需要pinRight来领养if (pminRight->_left == minRight) {pminRight->_left = minRight->_right;} else {// 如果不是,比如删除根节点,那么就需要将pminRight->_right指向minRight->right(最小值左边一定为NULL。不需要领养)//minRight是其父结点的右孩子pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;
}
递归函数
递归实现二叉搜索树的删除函数的思路如下:
- 若树为空树,则结点删除失败,返回false。
- 若所给key值小于树根结点的值,则问题变为删除左子树当中值为key的结点。
- 若所给key值大于树根结点的值,则问题变为删除右子树当中值为key的结点。
- 若所给key值等于树根结点的值,则根据根结点左右子树的存在情况不同,进行不同的处理。
bool _EraseR(Node *&root, const K &key) {if (root == nullptr)return false;if (key > root->_key) {return _EraseR(root->_right, key);} else if (key < root->_key) {return _EraseR(root->_left, key);} else {Node *del = root;//开始准备删除,root谁上层root->_left/_right的引用if (root->_right == nullptr) {//root是上层的左右子树root = root->_left;} else if (root->_left == nullptr) {root = root->_right;} else {Node *maxleft = root->_left;//找最大,最大在右边while (maxleft->_right) {maxleft = maxleft->_right;}swap(root->_key, maxleft->_key);//转换在子树去删除//这里不能传maxleft,maxleft是局部变量return _EraseR(root->_left, key);}delete del;return true;}
}
完整代码
//BSTree.h
#pragma once
#include <iostream>
using namespace std;template<class K>
// 二叉树的结构
struct BSTreeNode {BSTreeNode<K> *_left; //左孩子指针BSTreeNode<K> *_right;//右孩子指针K _key; //结点值//构造函数BSTreeNode(const K &key = 0): _left(nullptr), _right(nullptr), _key(key) {}
};template<class K>
class BSTree {typedef BSTreeNode<K> Node;public:BSTree() = default;//指定强制生成默认构造//默认构造,构造一个空树//构造树的深拷贝BSTree(const BSTree<K> &t) {_root = Copy(t._root);}//传统写法const BSTree<K> &operator=(const BSTree<K> &t) {//避免自己拷贝自己if (this != &t) {_root = Copy(t._root);}return *this;//为了支持连续赋值}//现代写法,接收一个t的拷贝,临时对象,然后进行交换BSTree<K> &operator=(BSTree<K> t) {swap(_root, t._root);return *this;}//析构函数~BSTree() {Destroy(_root);}bool Insert(const K &key) {// 如果根一开始就为nullptr,那么就直接构建初始的根if (_root == nullptr) {_root = new Node(key);return true;}// 如果_root不为nullptr,那么就从根开始遍历,找适合的位置Node *parent = nullptr;// parent跟着cur遍历找到合适的位置,充当插入的父亲节点Node *cur = _root;while (cur) {//key < cur->_key 需要走左子树//key > cur->_key 需要走右子树if (key < cur->_key) {parent = cur; //记录父亲结点cur = cur->_left;//走左树} else if (key > cur->_key) {parent = cur;cur = cur->_right;//走右数} else {// 如果key == cur->_key 那么就直接返回false,二叉搜索树的值不允许相同return false;}}// 找到后就开始链接cur = new Node(key);// 这里不知道cur最终走到了parent的左边还是右边,所以还要进行判断// key>parent->_key 链接右树// key<parent->_key 链接左树if (key > parent->_key) {parent->_right = cur;//右树} else if (key < parent->_key) {parent->_left = cur;//左树}return true;}// 查找bool Find(const K &key) {Node *cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;} else if (key < cur->_key) {cur = cur->_left;} else {return true;}}return false;}// 删除bool Erase(const K &key) {Node *parent = nullptr;Node *cur = _root;while (cur) {if (key > cur->_key) {parent = cur;cur = cur->_right;} else if (key < cur->_key) {parent = cur;cur = cur->_left;} else {// 开始删除// 1.如果要删除的cur左边是nullptr,那么我们就进行判断,判断cur在parent的左子树还是右子树,// 如果是左子树,那么就由parent的left指向cur的右子树,如果是右子树,就由parent的right指向cur的右子树if (cur->_left == nullptr) {// if (parent == nullptr)if (cur == _root) {_root = cur->_right;} else {if (parent->_left == cur) {parent->_left = cur->_right;} else {parent->_right = cur->_right;}}delete cur;} else if (cur->_right == nullptr) {// 2.cur的右边为nullptr// if (parent == nullptr)if (cur == _root) {_root = cur->_left;} else {if (parent->_left == cur) {parent->_left = cur->_left;} else {parent->_right = cur->_left;}}delete cur;} else {// 都不为nullptr,替代法,用被删除的cur的左子树的最大节点,右子树的最大节点替换// 找cur右子树的最大节点Node *pminRight = cur;Node *minRight = cur->_right;// 找右子树,右子树的最小位置在右子树的左边while (minRight->_left) {pminRight = minRight;minRight = minRight->_left;}// 找到最小的值赋值给curcur->_key = minRight->_key;// pminRight->_left==minRight 那么左边已经是最小了,所以minRight的左子树肯定为空了// 那么可能minRight还有右子树,所以需要pinRight来领养if (pminRight->_left == minRight) {pminRight->_left = minRight->_right;} else {// 如果不是,比如删除根节点,那么就需要将pminRight->_right指向minRight->right(最小值左边一定为NULL。不需要领养)//minRight是其父结点的右孩子pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}bool _FindR(Node *root, const K &key) {if (root == nullptr) {return false;}if (root->_key == key) {return true;}if (key > root->_key) {return _FindR(root->_right, key);} else {return _FindR(root->_left, key);}}Node *Copy(Node *root) {if (root == nullptr) {return nullptr;}//前序遍历copy树Node *newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node *&root) {if (root == nullptr) {return;}//后序遍历析构Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool FindR(const K &key) {return _FindR(_root, key);}bool _InsertR(Node *&root, const K &key) {if (root == nullptr) {root = new Node(key);return root;}if (key > root->_key) {return _InsertR(root->_right, key);} else if (key < root->_key) {return _InsertR(root->_left, key);} else {return false;}}bool InsertR(const K &key) {return _InsertR(_root, key);}bool _EraseR(Node *&root, const K &key) {if (root == nullptr)return false;if (key > root->_key) {return _EraseR(root->_right, key);} else if (key < root->_key) {return _EraseR(root->_left, key);} else {Node *del = root;//开始准备删除,root谁上层root->_left/_right的引用if (root->_right == nullptr) {//root是上层的左右子树root = root->_left;} else if (root->_left == nullptr) {root = root->_right;} else {Node *maxleft = root->_left;//找最大,最大在右边while (maxleft->_right) {maxleft = maxleft->_right;}swap(root->_key, maxleft->_key);//转换在子树去删除//这里不能传maxleft,maxleft是局部变量return _EraseR(root->_left, key);}delete del;return true;}}bool EraseR(const K &key) {return _EraseR(_root, key);}// 一般调用为t.InOrder() 不传参数,所以这里进行了封装void InOrder() {_InOrder(_root);cout << endl;}void _InOrder(Node *root) {if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node *_root = nullptr;// 二叉搜索树的根
};
测试代码:
#include "BSTree.h"void test_BStree1() {int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};BSTree<int> t;for (auto e: a) {t.Insert(e);}t.Erase(7);t.Erase(14);t.Erase(3);t.Erase(8);t.InOrder();
}void test_BSTree2() {int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};BSTree<int> t;for (auto e: a) {t.InsertR(e);}t.EraseR(7);t.EraseR(14);t.EraseR(3);t.EraseR(8);t.EraseR(6);t.InOrder();
}void test_BSTree3() {int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};BSTree<int> t1;for (auto e: a) {t1.InsertR(e);}t1.InOrder();BSTree<int> t2(t1);t2.InOrder();
}int main() {test_BSTree3();return 0;
}
二叉搜索树的应用
-
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
-
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
-
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
-
-
KV模型:每一个关键码key,都有与之对应的值Value,即<Key,Value>的键值对。该种方式在现实生活中非常常见:
-
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文**<word,chinese>**就构成一种键值对;
-
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数**,单词与其出现次数就是就构成一种键值对。**
-
KV结构的二叉搜索树:
#include <iostream>
#include <string>
using namespace std;
// 改造二叉搜索树为KV结构s
template<class K, class V>
struct BSTNode {BSTNode(const K &key = K(), const V &value = V()): _pLeft(nullptr), _pRight(nullptr), _key(key), _Value(value) {}BSTNode<K, V> *_pLeft;BSTNode<K, V> *_pRight;K _key;V _value
};template<class K, class V>
class BSTree {typedef BSTNode<K, V> Node;typedef Node *PNode;public:BSTree() : _pRoot(nullptr) {}PNode Find(const K &key);bool Insert(const K &key, const V &value);bool Erase(const K &key);private:PNode _pRoot;
};void TestBSTree3() {// 输入单词,查找单词对应的中文翻译BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("tree", "树");dict.Insert("left", "左边、剩余");dict.Insert("right", "右边");dict.Insert("sort", "排序");// 插入词库中所有单词string str;while (cin >> str) {BSTNode<string, string> *ret = dict.Find(str);if (ret == nullptr) {cout << "单词拼写错误,词库中没有这个单词:" << str << endl;} else {cout << str << "中文翻译:" << ret->_value << endl;}}
}
void TestBSTree4() {// 统计水果出现的次数string arr[] = {"苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉"};BSTree<string, int> countTree;for (const auto &str: arr) {// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的节点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == NULL) {countTree.Insert(str, 1);} else {ret->_value++;}}countTree.InOrder();
}
二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。 但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
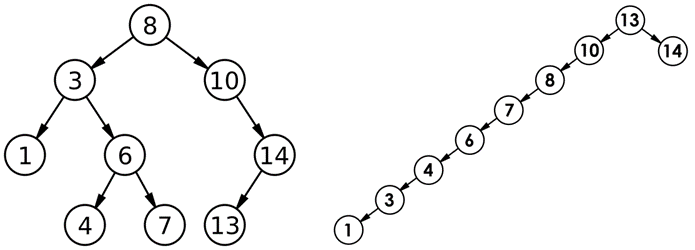
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:LogN
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N/2
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?答案就是使用AVL树和红黑树
相关文章:

【数据结构】C++实现二叉搜索树
二叉搜索树的概念 二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。若它的右子树不为空,则右子树上所有结点的值都大于根结…...

Python中Mock和Patch的区别
前言: 嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 在测试并行开发(TPD)中,代码开发是第一位的。 尽管如此,我们还是要写出开发的测试,…...
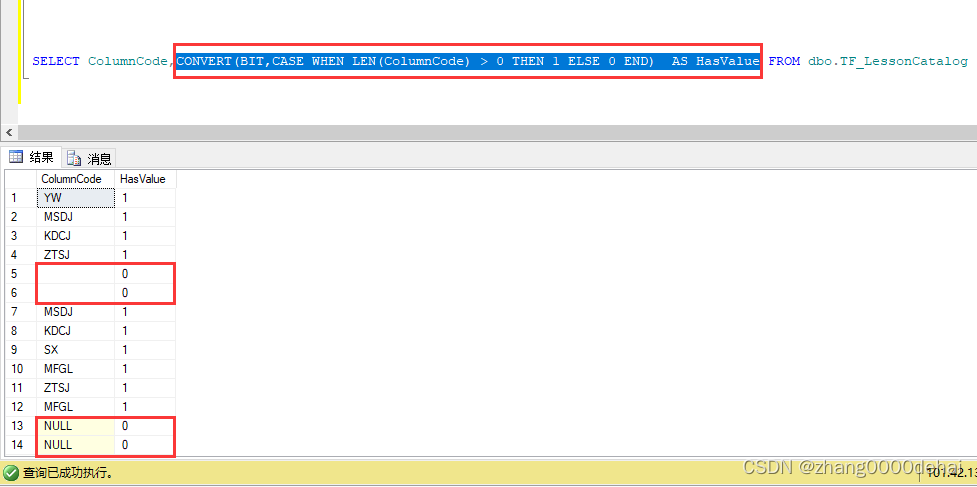
sql server 查询某个字段是否有值 返回bool类型
sql server 查询某个字段是否有值 返回bool类型,true 或 false SELECT ColumnCode,CONVERT(BIT,CASE WHEN LEN(ColumnCode) > 0 THEN 1 ELSE 0 END) AS HasValue FROM dbo.TF_LessonCatalog...

紫光展锐5G芯T820 解锁全新应用场景,让机器人更智能
数字经济的持续发展正推动机器人产业成为风口赛道。工信部数据显示,2023年上半年,我国工业机器人产量达22.2万套,同比增长5.4%;服务机器人产量为353万套,同比增长9.6%。 作为国内商用服务机器人领先企业,云…...

秋招前端面试题总结
1、this指向问题,以前总是迷糊,现在总算是一知半解了。应当遵循以下原则,应该就能做对题目了。 如果一个标准函数,也就是非箭头函数,作为某个对象的方法被调用时,那么这个this指向的就是这个对象。涉及到闭…...

【入门篇】ClickHouse 数据类型
文章目录 1. 引言2. ClickHouse 数据类型2.1 基本数据类型2.1.1 整型2.1.2 浮点型2.1.3 字符串型 2.2 复合数据类型2.2.1 数组2.2.2 枚举类型2.2.3 元组2.2.4 Map2.2.5 Nullable 2.3 特殊数据类型2.3.1 日期和时间类型2.3.2 UUID2.3.3 IP 地址2.3.4 AggregateFunction 2.4 数据…...

关于Python数据分析,这里有一条高效的学习路径
无处不在的数据分析 谷歌的数据分析可以预测一个地区即将爆发的流感,从而进行针对性的预防;淘宝可以根据你浏览和消费的数据进行分析,为你精准推荐商品;口碑极好的网易云音乐,通过其相似性算法,为不同的人…...

基于 json-server 工具,模拟实现后端接口服务环境
文章目录 本地配置后端接口一、安装json-server1、安装 JSON 服务器 安装 JSON 服务器2、创建一个db.json包含一些数据的文件(重点)3、启动 JSON 服务器 启动 JSON 服务器4、现在如果你访问http://localhost:3000/posts/1,你会得到 本地配置后…...

想要精通算法和SQL的成长之路 - 课程表II
想要精通算法和SQL的成长之路 - 课程表 前言一. 课程表II (拓扑排序)1.1 拓扑排序1.2 题解 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 课程表II (拓扑排序) 原题链接 1.1 拓扑排序 核心知识: 拓扑排序是专…...
【sgGoogleTranslate】自定义组件:基于Vue.js用谷歌Google Translate翻译插件实现网站多国语言开发
sgGoogleTranslate源码 <template><div :id"$options.name"> </div> </template> <script> export default {name: "sgGoogleTranslate",props: ["languages", "currentLanguage"],data() {return {//…...
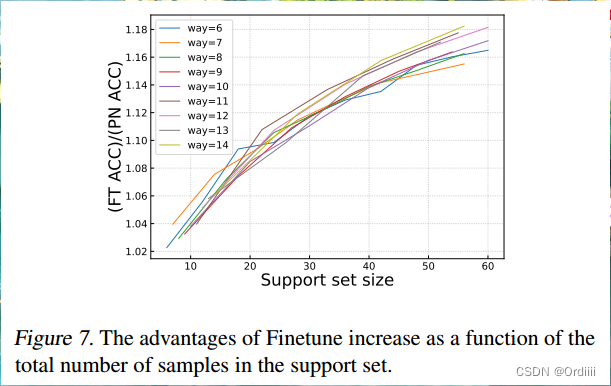
论文总结《A Closer Look at Few-shot Classification Again》
原文链接 A Closer Look at Few-shot Classification Again 摘要 这篇文章主要探讨了在少样本图像分类问题中,training algorithm 和 adaptation algorithm的相关性问题。给出了training algorithm和adaptation algorithm是完全不想关的,这意味着我们…...
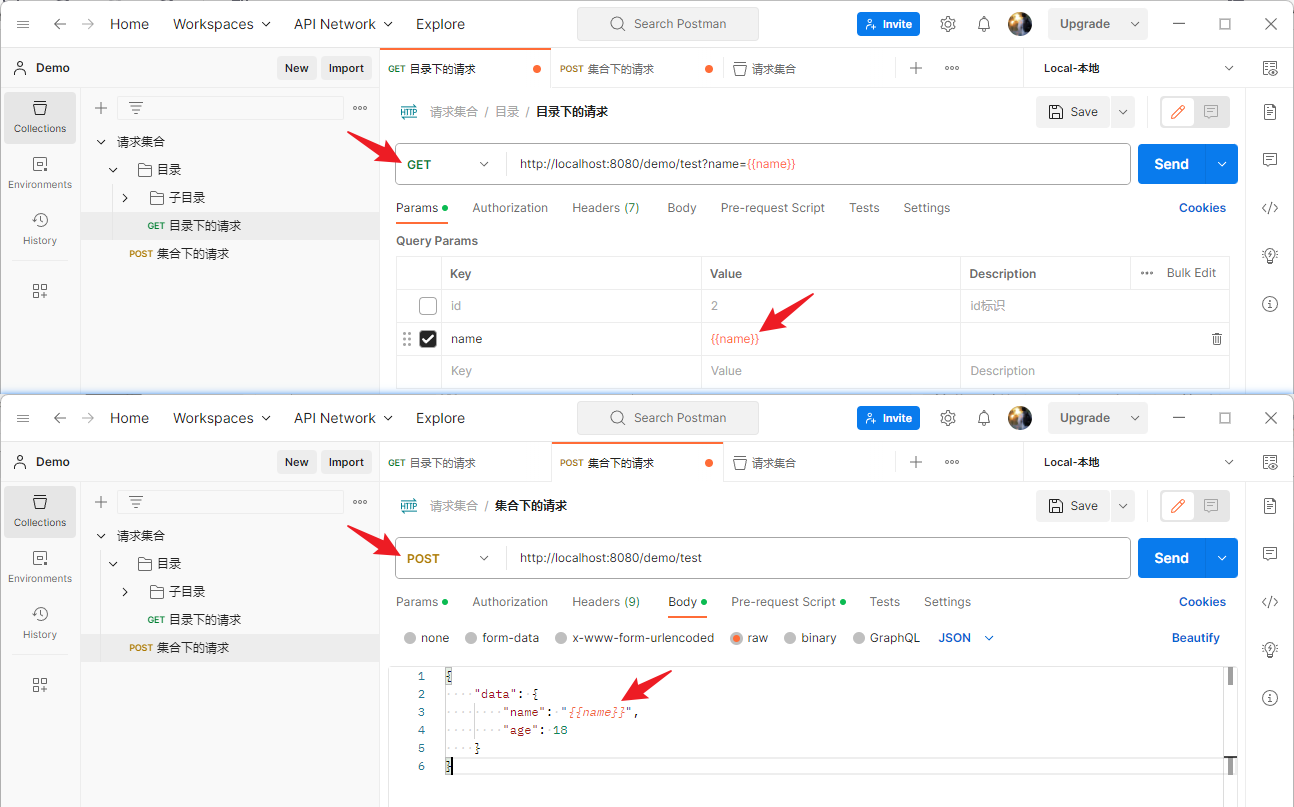
Postman使用_参数设置和获取
文章目录 参数引用内置动态参数手动添加参数脚本设置参数脚本获取参数 参数就像变量一样,它可以是固定的值,也可以是变化的值,比如:会根据一些条件或其他参数进行变化。我们如果要使用该参数就需要引用它。 参数引用 引用动态参数…...

【SQL】优化SQL查询方法
优化SQK查询 一、避免全表扫描 1、where条件中少使用! 或 <>操作符,引擎会放弃索引,进行全表扫描 2、in \or ,用between 或 exist 代替in 3、where 对字段进行为空判断 4、where like ‘%条件’ 前置百分号 5、where …...

Linux-相关操作
2.2.2 Linux目录结构 /:根目录,一般根目录下只存放目录,在Linux下有且只有一个根目录。所有的东西都是从这里开始。当你在终端里输入“/home”,你其实是在告诉电脑,先从/(根目录)开始…...
二十、MySQL多表关系
1、概述 在项目开发中,在进行数据库表结构设计时,会根据业务需求以及业务模块之间的关系,分析并设计表结构,由于业务之间相互关联,所以各个表结构之间也存在着各种对应关系 2、多表关系分类 (1࿰…...
HarmonyOS/OpenHarmony应用开发-DevEco Studio新建项目的整体说明
一、文件-新建-新建项目 二、传统应用形态与IDE自带的模板可供选用与免安装的元服与IDE中自带模板的选择 三、以元服务,远程模拟器为例说明IDE整体结构 1区是工程目录结构,是最基本的配置与开发路径等的认知。 2区是代码开发与修改区,是开发…...
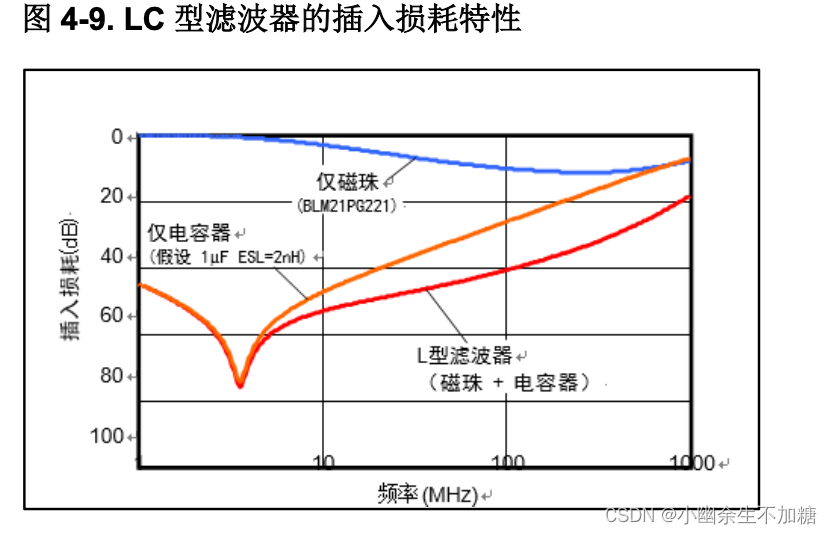
去耦电路设计应用指南(三)磁珠/电感的噪声抑制
(三)磁珠/电感的噪声抑制 1. 电感1.1 电感频率特性 2. 铁氧体磁珠3. LC 型和 PI 型滤波 当去耦电容器不足以抑制电源噪声时,电感器&磁珠/ LC 滤波器的结合使用是很有效的。扼流线圈与铁氧体磁珠 是用于电源去耦电路很常见的电感器。 1. …...

Spring Bean的获取方式
参考https://juejin.cn/post/7251780545972994108?searchId2023091105493913AF7C1E3479BB943C80#heading-12 记录并补充 1.通过BeanFactoryAware package com.toryxu.demo1.beans;import org.springframework.beans.BeansException; import org.springframework.beans.facto…...

4795-2023 船用舱底水处理装置 学习记录
声明 本文是学习GB-T 4795-2023 船用舱底水处理装置. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本文件规定了船用舱底水处理装置(以下简称处理装置)中舱底水分离器(以下简称分离器)和舱底 水报警装置(以下简称报警装置)的要求、试验方法…...
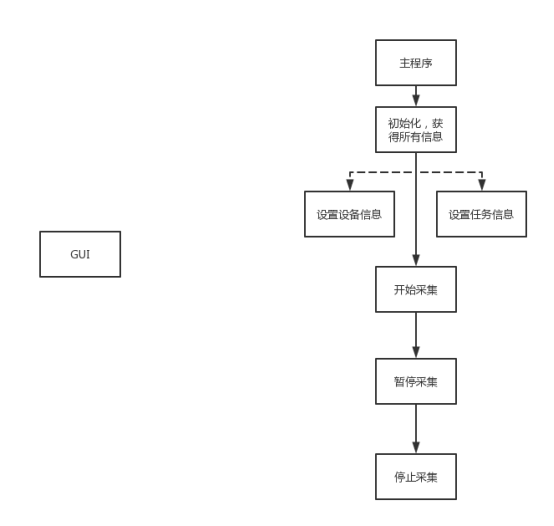
[框架设计之道(二)]设备、任务设置及业务流程
[框架设计之道(二)]设备、任务设置及业务流程 说明 此文档是开发中对设备设置项的管理。因为硬件在使用的过程中涉及大量设置项,因此需要单独开一篇文档说明设备的设置和任务的设置。 一、设备设置 1.基础接口 /// <summary> /// 配置…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
