线程安全问题的原因及解决方案
要想知道线程安全问题的原因及解决方案,首先得知道什么是线程安全,想给出一个线程安全的确切定义是复杂的,但我们可以这样认为:如果多线程环境下代码运行的结果是符合我们预期的,即在单线程环境应该的结果,则说这个程序是线程安全的。例如:使用两个线程分别对同一个变量进行修改,得出的结果与使用一个线程对这个变量进行修改的结果不同,这样的问题就可以说是该程序不是线程安全的。知道了什么是线程安全后,这样才好分析线程安全问题的原因及解决方案。
原因1)多个线程之间的调度顺序是随机的,操作系统使用抢占式策略来执行线程(根本原因),并且该原因无法改变,当前主流的操作系统都是如此:例如当两个线程分别对同时一个变量count++,则会使每次得到的结果不同,因为CPU的调度是抢占式的,且count++实际上有着三步操作,这就将导致得到的结果不同。因为count++的三步操作为:

public static volatile int count = 0;//倘若没有volatile,则该代码会一直进行下去
public static void main(String[] args) throws InterruptedException {Thread t1 = new Thread(() -> {while(count == 0){;}});Thread t2 = new Thread(() -> {try {Thread.currentThread().sleep(1000);} catch (InterruptedException e) {e.printStackTrace();}count = 1;});t1.start();t2.start();t1.join();
}
相关文章:

线程安全问题的原因及解决方案
要想知道线程安全问题的原因及解决方案,首先得知道什么是线程安全,想给出一个线程安全的确切定义是复杂的,但我们可以这样认为:如果多线程环境下代码运行的结果是符合我们预期的,即在单线程环境应该的结果,…...
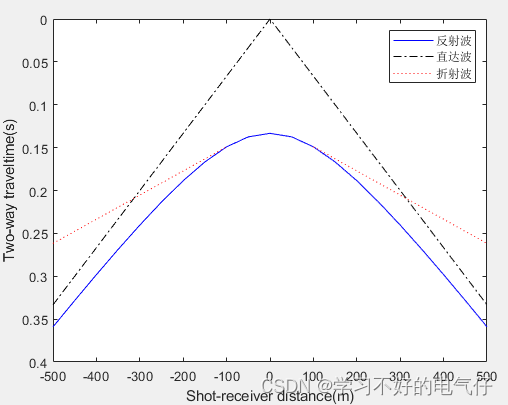
基于matlab中点放炮各类地震波时距曲线程序
完整程序: clear all dx50;x-500:dx:500;%炮检距 h100;V11500; theta25*pi/180; V2V1/sin(theta); t1sqrt(x.*x4*h*h)/V1;%反射波时距曲线 t2abs(x)./V1;%直达波时距曲线 %折射波时距曲线 xm2*h*tan(theta);%求盲区 k1; for i1:length(x) if x(i)<-xm …...

vue中el-dialog 中的内容没有预先加载,因此无法获得内部元素的ref 的解决方案 使用强制提前加载dialog方法
问题描述 在没有进行任何操作的时候,使用 this.$refs.xxxx 无法获取el-dialog中的内部元素,这个问题会导致很多bug,其中目前网络上也有许多关于这个问题的解决方案,但是大多数是使用el-dialog中的open在dialog打开的时候使用thi…...

vue-h5移动Web的rem配置
H5移动的适配方案 rem rem适配方案是兼容性比较好的移动端适配方案,rem支持大部分的移动端系统和机型。 rem是相对于根元素的字体大小的单位。本质上就是一个相对单位,和em的区别是:em是依赖父元素的字体来计算,rem是依赖根元素…...
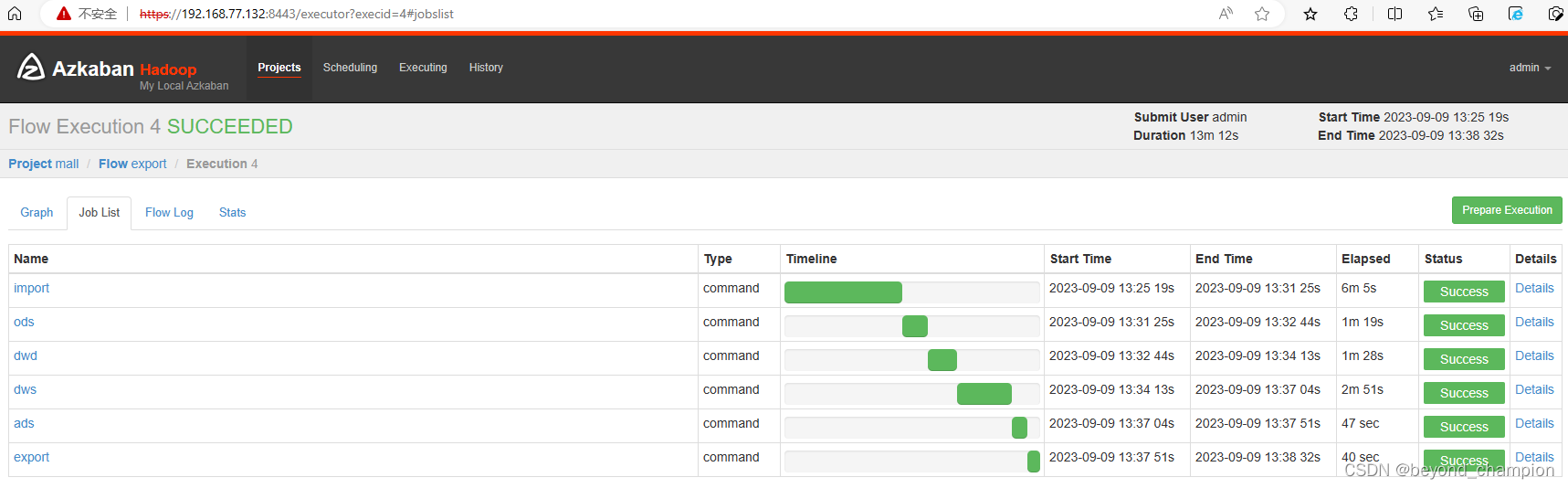
企业级数据仓库-数仓实战
数仓实战 安装包大小 安装清单 环境搭建 一、环境搭建01(机器准备) 准备好三台虚拟机,并进行修改hostname、在hosts文件增加ip地址和主机名映射 。 1、设置每个虚拟机的hostname vi /etc/sysconfig/network 修改HOSTNAMEnode02修改hostna…...

Spring Boot 下载文件(word/excel等)文件名中文乱码问题|构建打包不存在模版文件(templates等)
Spring Boot 下载文件(word/excel等)文件名中文乱码问题|构建打包不存在模版文件(templates等) 准备文件,这里我放在resource下的templates路径 在pom中配置构建打包的资源,更新maven 如果使用了assembly打包插件这样配置可能仍不生效&#…...

Ansible数组同步至Shell脚本数组中
1、ansible中定义数组,我以 ccaPojectList 数组为例子,如下图数组内容 2、需要写一个j2模板的Shell脚本,在j2模板的Shell脚本中引用ansible的 ccaPojectList 数组,大致如下图: {% for item in ccaPojectList %} "{{ item }…...
私域流量的优势
私域流量是指由自身品牌或个人拥有并具备完全掌控权的流量资源。它相比于传统的广告推广,拥有独特的优势。 首先,私域流量能够更加精准地定位目标用户,实现精准传播。不再盲目投放广告,而是通过建立自身社群、粉丝群,获…...

Java 中“1000==1000”为false,而”100==100“为true?
如果你运行下面的代码: Integer a 1000, b 1000; System.out.println(a b);//1Integer c 100, d 100; System.out.println(c d);//2你会得到: false true基本知识:我们知道,如果两个引用指向同一个对象,用表示它们是相等的。如果两…...
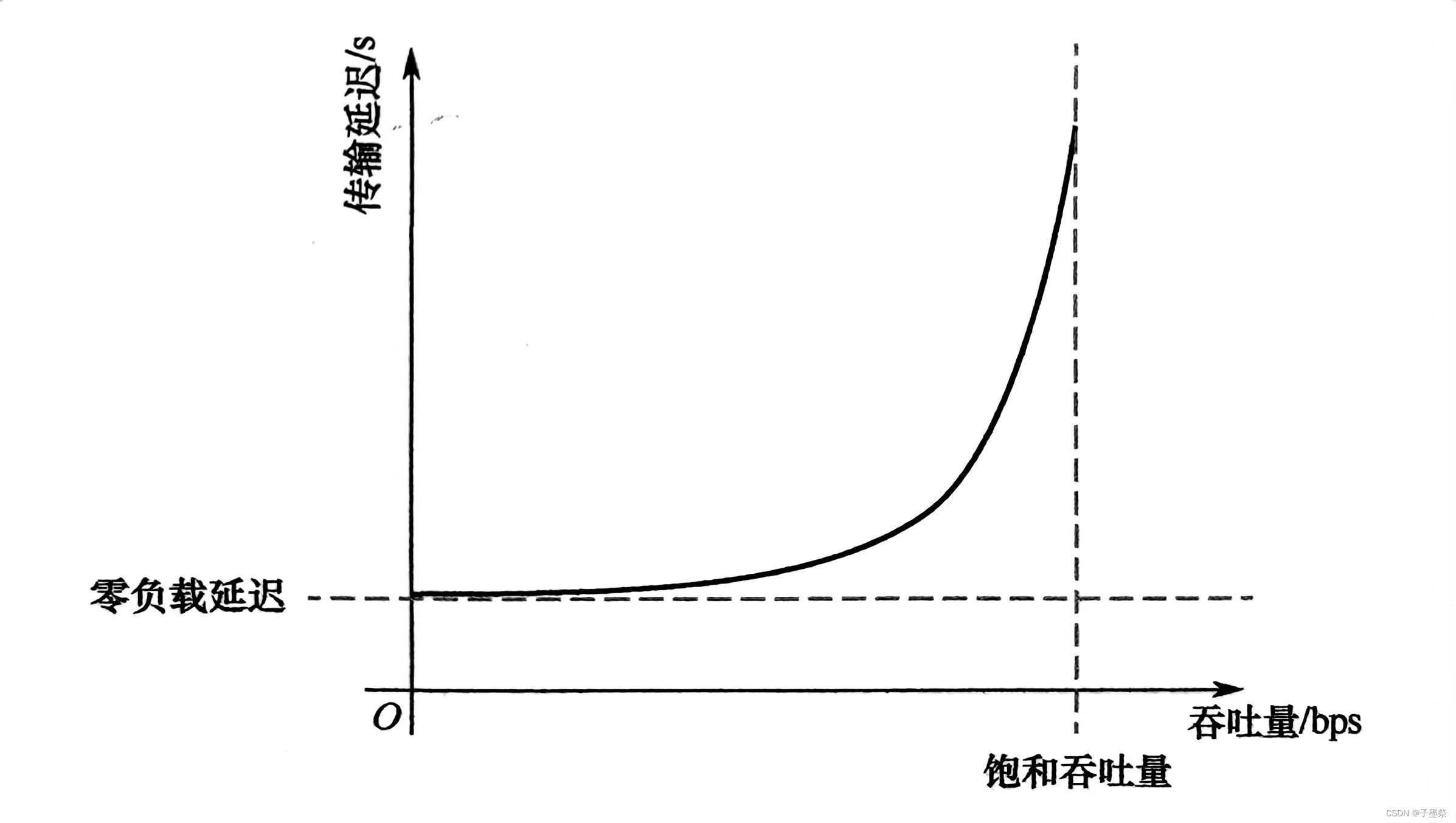
片上网络(1)概述
前言 NoC:On-Chip Networks,片上网络。 由于多核乃至众核时代的到来,用于连接它们的可扩展、低延迟、大带宽的通信结构变得至关重要。 在核心较少时,总线Bus和矩阵/交叉开关Crossbar是主要的互联结构。总线可以提供较低的传输延迟…...

使用 React Native 针对 Android 进行开发
🎬 岸边的风:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 概述 通过安装所需工具开始使用 React Native 创建新的 React Native 项目 本指南将有助于开始使用 Windows 上的…...

LeetCode 每日一题 2023/9/11-2023/9/17
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 9/11 630. 课程表 III9/12 1462. 课程表 IV9/13 2596. 检查骑士巡视方案9/14 1222. 可以攻击国王的皇后9/15 LCP 50. 宝石补给9/16 198. 打家劫舍9/17 9/11 630. 课程表 II…...

Linux系统调试篇——GDBSERVER远程调试
文章目录 安装 GDBSERVERgdbserver 用法具体步骤 本篇讲解如何使用gdbserver对目标开发板上的程序进行远程调试。 安装 GDBSERVER 首先在开发板上安装 gdbserver: apt install gdbservergdbserver 用法 gdbserver用法描述: Usage: gdbserver [OPTION…...

前端实现打字效果
前端实现打字效果 不带光标 只一次播放 HTML <!-- 需要在初始化的时候不显示文字 --> <div id"typing"></div>CSS #typing {position: relative;font-size: 24px;font-family: Arial, sans-serif;padding: 10px; }JS const text "要显…...

Unix和Linux、GNU和GPL、RHEL和Centos、Debian和Ubuntu
文章目录 Unix和LinuxGNU和GPLGNU/Linux名称的来源RHEL和CentosDebian和Ubuntu 以上都是操作系统,服务器操作系统、桌面操作系统。 对于刚刚接触Linux系统或者从事运维相关工作的人来说,肯定会听过很多名词,但是不知道他们的区别和联系&#…...

InfiniBand vs 光纤通道,存储协议的选择
数字时代,数据量爆发增长,企业越来越迫切地追求高吞吐量、低延迟和更高性能的网络基础设施,存储协议的选择变得愈发至关重要。在众多存储协议中,InfiniBand和光纤通道备受关注。本文旨在深入探讨InfiniBand和光纤通道作为存储协议…...

第2章_freeRTOS入门与工程实践之单片机程序设计模式
本教程基于韦东山百问网出的 DShanMCU-F103开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id724601559592 配套资料获取:https://rtos.100ask.net/zh/freeRTOS/DShanMCU-F103 freeRTOS系列教程之freeRTOS入…...

python LeetCode 刷题记录 58
题目 给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。 示例 输入:s "Hello World" 输出:5 解释&am…...

HarmonyOS开发:那些开发中常见的问题汇总(一)
前言 本来这篇文章需要讲述静态共享包如何实现远程依赖和上传以及关于静态共享包私服的搭建,非常遗憾的告诉大家,由于组织管理申请迟迟未通过,和部分文档官方权限暂未开放,关于这方面的讲解需要延后了,大概需要等到202…...
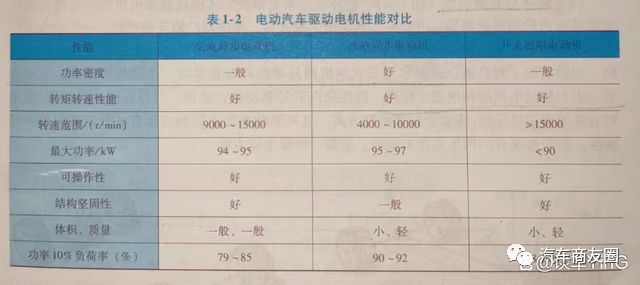
新能源汽车驱动电机的基本知识
学习目标:了解电机的基本知识。能力目标:培养学生搜集和整理相关资料的能力。素质目标:培养学生良好的职业素养。额定电店.在夫见定条件下电池工作的*于佳 电压知识准备术语和定义。 (1)驱动电机系统 通过有效的控制策略将动力蓄电池提供的直流电转化为交流实现电机的正转以及反…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
