第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导
第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导
本篇博客精简自本人关于曲面积分的博客:详情见:曲面积分(Surface Integral)
曲面参数化(曲面上的每个点都使用起点为原点、终点为该曲面上的点的向量表示)
x o y xoy xoy平面中区域 R R R(其实是曲面在 x o y xoy xoy平面上的投影)上方的曲面,其参数表示式 r ( u , v ) = f ( u , v ) i + g ( u , v ) j + h ( u , v ) k \bold{r}(u,v)=f(u,v)\bold{i}+g(u,v)\bold{j}+h(u,v)\bold{k} r(u,v)=f(u,v)i+g(u,v)j+h(u,v)k

点 P P P处的沿 u u u轴和 v v v轴的切向量分别是:
r u = ∂ r ( u , v ) ∂ u = ∂ f ( u , v ) ∂ u i + ∂ g ( u , v ) ∂ u j + ∂ h ( u , v ) ∂ u k \bold{r_u}=\frac{\partial \bold{r}(u,v)}{\partial u}=\frac{\partial f(u,v)}{\partial u}\bold{i}+\frac{\partial g(u,v)}{\partial u}\bold{j}+\frac{\partial h(u,v)}{\partial u}\bold{k} ru=∂u∂r(u,v)=∂u∂f(u,v)i+∂u∂g(u,v)j+∂u∂h(u,v)k
r v = ∂ r ( u , v ) ∂ v = ∂ f ( u , v ) ∂ v i + ∂ g ( u , v ) ∂ v j + ∂ h ( u , v ) ∂ v k \bold{r_v}=\frac{\partial \bold{r}(u,v)}{\partial v}=\frac{\partial f(u,v)}{\partial v}\bold{i}+\frac{\partial g(u,v)}{\partial v}\bold{j}+\frac{\partial h(u,v)}{\partial v}\bold{k} rv=∂v∂r(u,v)=∂v∂f(u,v)i+∂v∂g(u,v)j+∂v∂h(u,v)k

点P处的沿 u u u轴和 v v v轴的切向量叉乘的数值大小为两个切向量组成四边形的面积,使用该面积替代下方的曲面微元(以直平面替代曲面)
S 1 = ∣ r u × r v ∣ S_1=|\bold{r_u}×\bold{r_v}| S1=∣ru×rv∣

对 r u 、 r v r_u、r_v ru、rv进行缩放调整其大小基本和下方曲面边长大小差不多, Δ u r u 、 Δ v r v \Delta ur_u、\Delta vr_v Δuru、Δvrv,现在直平面面积变为了
S = ∣ Δ u r u × Δ v r v ∣ = ∣ r u × r v ∣ Δ u Δ v ≈ Δ σ x y S=|\Delta ur_u×\Delta vr_v|=|\bold{r_u}×\bold{r_v}|\Delta u\Delta v\approx \Delta\sigma_{xy} S=∣Δuru×Δvrv∣=∣ru×rv∣ΔuΔv≈Δσxy

曲面微元 d σ d\sigma dσ与 d u d v dudv dudv之间的关系
d σ = ∣ r u × r v ∣ d u d v d\sigma=|\bold{r_u}×\bold{r_v}|dudv dσ=∣ru×rv∣dudv
若曲面的面密度不是常数,即被积函数不是常数,则曲面S质量为:
∬ S G ( x , y , z ) d σ = ∬ R G ( f ( u , v ) , g ( u , v ) , h ( u , v ) ) ∣ r u × r v ∣ d u d v \iint\limits_{S}G(x,y,z)d\sigma=\iint\limits_{R}G(f(u,v),g(u,v),h(u,v))|\bold{r_u}×\bold{r_v}|dudv S∬G(x,y,z)dσ=R∬G(f(u,v),g(u,v),h(u,v))∣ru×rv∣dudv
若我们取 x = u 、 y = v 、 z = f ( x , y ) x=u、y=v、z=f(x,y) x=u、y=v、z=f(x,y),其中 z = f ( x , y ) z=f(x,y) z=f(x,y)是 x o y xoy xoy平面中区域 R R R上的曲面表达式
参数化后曲面的表示式
r ( u , v ) = u i + v j + f ( u , v ) k \bold{r}(u,v)=u\bold{i}+v\bold{j}+f(u,v)\bold{k} r(u,v)=ui+vj+f(u,v)k
点P处的沿 u u u轴和 v v v轴的切向量分别是:
r u = ∂ r ( u , v ) ∂ u = i + f u ′ ( u , v ) k \bold{r_u}=\frac{\partial \bold{r}(u,v)}{\partial u}=\bold{i}+f'_u(u,v)\bold{k} ru=∂u∂r(u,v)=i+fu′(u,v)k
r v = ∂ r ( u , v ) ∂ v = j + f v ′ ( u , v ) k \bold{r_v}=\frac{\partial \bold{r}(u,v)}{\partial v}=\bold{j}+f'_v(u,v)\bold{k} rv=∂v∂r(u,v)=j+fv′(u,v)k
r u × r v = ∣ i j k 1 0 f u ′ 0 1 f v ′ ∣ = − f u ′ i − f v ′ j + k \bold{r_u}×\bold{r_v}=\left | \begin{matrix} \bold{i}&\bold{j}&\bold{k}\\ 1 & 0 & f'_u \\ 0 & 1 & f'_v \\ \end{matrix} \right | =-f'_u\bold{i}-f'_v\bold{j}+\bold{k} ru×rv= i10j01kfu′fv′ =−fu′i−fv′j+k
∣ r u × r v ∣ = ( − f u ′ ) 2 + ( − f v ′ ) 2 + 1 2 = f u ′ 2 + f v ′ 2 + 1 |\bold{r_u}×\bold{r_v}|=\sqrt{(-f'_u)^2+(-f'_v)^2+1^2}=\sqrt{f'^2_u+f'^2_v+1} ∣ru×rv∣=(−fu′)2+(−fv′)2+12=fu′2+fv′2+1
∣ r u × r v ∣ d u d v = ( − f u ′ ) 2 + ( − f v ′ ) 2 + 1 2 d u d v = f u ′ 2 + f v ′ 2 + 1 d u d v |\bold{r_u}×\bold{r_v}|dudv=\sqrt{(-f'_u)^2+(-f'_v)^2+1^2}dudv=\sqrt{f'^2_u+f'^2_v+1}dudv ∣ru×rv∣dudv=(−fu′)2+(−fv′)2+12dudv=fu′2+fv′2+1dudv
将参数化后的参数替换为原参 x = u 、 y = v x=u、y=v x=u、y=v
曲面微元 d σ d\sigma dσ与其投影面积微元 d x d y dxdy dxdy之间的关系
d σ = f x ′ 2 + f y ′ 2 + 1 d x d y d\sigma=\sqrt{f'^2_x+f'^2_y+1}dxdy dσ=fx′2+fy′2+1dxdy
区域R(曲面投影)上方曲面的面积为:
∬ R d σ = ∬ R f x ′ 2 + f y ′ 2 + 1 d x d y \iint\limits_{R}d\sigma=\iint\limits_{R}\sqrt{f'^2_x+f'^2_y+1}dxdy R∬dσ=R∬fx′2+fy′2+1dxdy
曲面显式表达式: z = f ( x , y ) z=f(x,y) z=f(x,y),曲面隐式表达式: G ( x , y , z ) = z − f ( x , y ) G(x,y,z)=z-f(x,y) G(x,y,z)=z−f(x,y)
G x ′ ( x , y , z ) = − f x ′ ( x , y ) G y ′ ( x , y , z ) = − f y ′ ( x , y ) G z ′ ( x , y , z ) = 1 G'_x(x,y,z)=-f'_x(x,y)\\ ~\\ G'_y(x,y,z)=-f'_y(x,y)\\ ~\\ G'_z(x,y,z)=1 Gx′(x,y,z)=−fx′(x,y) Gy′(x,y,z)=−fy′(x,y) Gz′(x,y,z)=1
若曲面的面密度不是常数,即被积函数不是常数,则曲面S质量为:
∬ S G ( x , y , z ) d σ = ∬ R G ( x , y , f ( x , y ) ) f x ′ 2 + f y ′ 2 + 1 d x d y \iint\limits_{S}G(x,y,z)d\sigma=\iint\limits_{R}G(x,y,f(x,y))\sqrt{f'^2_x+f'^2_y+1}dxdy S∬G(x,y,z)dσ=R∬G(x,y,f(x,y))fx′2+fy′2+1dxdy
相关文章:

第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导
第一类曲面积分:曲面微元dσ与其投影面积微元dxdy之间的关系推导 本篇博客精简自本人关于曲面积分的博客:详情见:曲面积分(Surface Integral) 曲面参数化(曲面上的每个点都使用起点为原点、终点为该曲面上的点的向量表示&#x…...

vue学习之Font Awesome图标
官方文档 https://fontawesome.com.cn/v5 Font Awesome 安装 cnpm install font-awesome/src/main.js 引入css import Vue from vue; import ElementUI from element-ui; import element-ui/lib/theme-chalk/index.css; import App from ./App.vue;...

mysql内连接与外连接详解
内连接与外连接 内连接外连接 在数据库中,连接操作是一种把两个或者多个表的记录组合在一起的操作,常用的有内连接(Inner Join)、外连接(Outer Join)等。 内连接 内连接(Inner Join࿰…...

在Mujoco环境下详细实现PPO算法应用于Humanoid-v2的完整教程
第一部分:介绍 1. 背景介绍 MuJoCo,或称为多关节动力学与控制的物理引擎,已经成为了强化学习中仿真环境的首选工具。其精确的物理仿真和高效的速度使得研究者可以在这个环境下测试和验证各种算法。PPO,即近端策略优化,是一种深度强化学习中的策略优化方法。它解决了TRPO…...
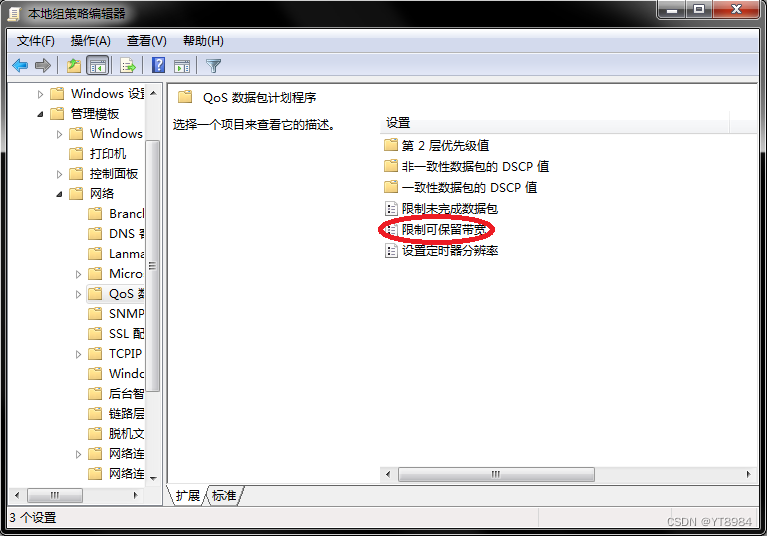
怎么给网络加速
首先,按winr,调出运行窗口。 输入cmd,回车,再输入gpedit.msc,调出本地组策略编辑器。 点击计算机配置下的管理模版。 再点击网络。 再点击Qos数据包计划程序。 再点击限制可保留宽带。 选择已启用,再把带宽…...
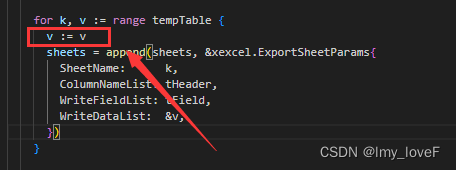
golang for循环append的数据重复
原因,因为使用了& 需要增加一行,问题解决...
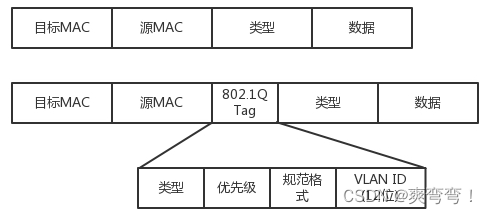
趣谈网络协议_1
趣谈网络协议_1 第1讲 | 为什么要学习网络协议?第4讲 | DHCP与PXE:IP是怎么来的,又是怎么没的?动态主机配置协议(DHCP) 第5讲 | 从物理层到MAC层:如何在宿舍里自己组网玩联机游戏?第…...

利用WebStorm开发react——本文来自AI创作助手
要在WebStorm中开发React应用程序,请按照以下步骤进行设置: 1.安装Node.js和npm(如果尚未安装)。 2.下载和安装WebStorm。 3.打开WebStorm,并在欢迎界面中选择“Create New Project”。 4.在弹出窗口中,…...

将本地构建的镜像推送到远程镜像库,构建多种系统架构支持的Docker镜像并推送到Docker Hub
目录 推送到 Docker Hub前提:需要在 [Docker Hub](https://hub.docker.com/) 创建账户、创建仓库。1. 创建 Dockerfile 和构建镜像:docker build -t2. 登录到远程镜像库:docker login3. 将镜像标记为远程仓库地址:docker tag4. 推…...

【技术分享】NetLogon于域内提权漏洞(CVE-2020-1472)
一、漏洞介绍 CVE-2020-1472是一个Windows域控中严重的远程权限提升漏洞。攻击者在通过NetLogon(MS-NRPC)协议与AD域控建立安全通道时,可利用该漏洞将AD域控的计算机账号密码置为空,从而控制域控服务器。该漏洞适用于Win2008及后…...

python学习之【模块】
前言 上一篇文章 python学习之【深拷贝】中学习了python中的深浅拷贝学习内容,这篇文章接着学习python中的模块。 什么是模块 在python中,一个文件(以“.py”为后缀名的文件)就叫做一个模块,每一个模块在python里都…...

dns电脑服务器发生故障怎么修复
DNS电脑服务器发生故障可能会导致网络连接问题、网页无法访问、或者电子邮件无法发送等情况。修复DNS电脑服务器故障可以采取多种方法,例如检查网络连接、更换DNS服务器等措施。当DNS电脑服务器发生故障时,可以采取以下修复措施: 尝试刷新DNS…...

Python项目Flask ipv6双栈支持改造
一、背景 Flask 是一个微型的(轻量)使用Python 语言开发的 WSGI Web 框架(一组库和模块),基于Werkzeug WSGI工具箱/库和Jinja2 模板引擎,当然,Python的WEB框架还有:Django、Tornado、Webpy,这暂且不提。 Flask使用BSD授权。 Flask也被称为microframework(微框架),F…...

hcia 目的mac为(单播 组播 广播)mac
从下往上看...
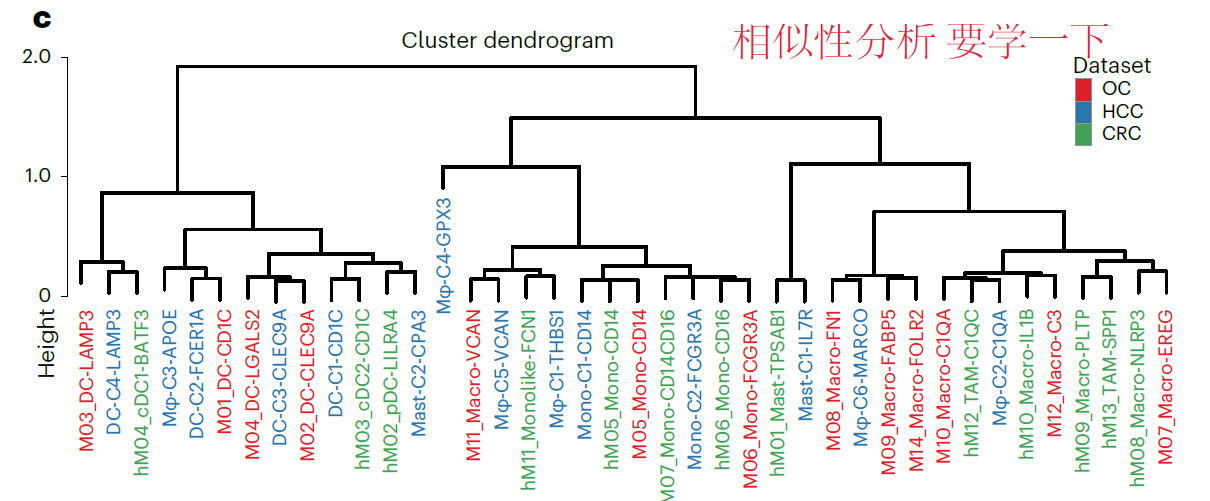
专栏十:10X单细胞的聚类树绘图
经常在文章中看到对细胞群进行聚类,以证明两个cluster之间的相关性,这里总结两种绘制这种图的方式和代码,当然我觉得这些五颜六色的颜色可能是后期加的,本帖子只总结画树状图的方法 例一 文章Single-cell analyses implicate ascites in remodeling the ecosystems of pr…...

linux查找命令使用的正则表达式
正则表达式是一种用于匹配和操作文本的强大工具,它是由一系列字符和特殊字符组成的模式,用于描述要匹配的文本模式。 正则表达式可以在文本中查找、替换、提取和验证特定的模式。 一般的查找命令是:grep,sed,awk 元字…...
ffmpeg6.0编译(NDK)
ffmpeg 6.0 支持vulkan 需要手动安装Vulkan 并将include里面的vk_video 和 vulkan 拷贝到 android-ndk-r25c/toolchains/llvm/prebuilt/linux-x86_64/sysroot/usr/include/ vulkan 下载 cp -r vk_video $NDK_HOME/toolchains/llvm/prebuilt/linux-x86_64/sysroot/usr/include/…...

达观RPA实战-编码与解码
一、应用背景 项目中我们经常需要获取某个服务的JSON数据。如果响应返回的是JSON格式的数据,客户端通过JSON工具可正常解析。但如果碰到值里面有中文的,特别是返回的格式是类似“{"name": "\u5927\u7231\u4e2d\u56fd"}”处理起来会比较麻烦。本文将从编…...

配置Swagger开发环境有效,生产环境无效
安全扫描:通用信息泄漏【未授权访问ip:端口号/swagger-ui.html】 步骤一:配置启用变量【开发环境可用生产环境不可用】 application-dev.yml: swagger:enable: true application-pro.yml: swagger:enable: false 步骤二:根据配置变量控…...
)
Jmeter系列-线程组的执行顺序(10)
重点 每个测试计划至少需要有一个线程组 线程组下不同组件的执行优先级/顺序 1、配置元件、监听器 2、前置处理器 3、定时器 4、逻辑控制器 5、取样器 6、后置处理器 7、断言 取样器执行顺序 在没有逻辑控制器情况下,取样器是按从上往下的顺序执行的 参考文章…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
