高阶数据结构(2)-----红黑树(未完成)
一)红黑树的基本概念和基本性质:
1)红黑树就是一种高度平衡的二叉搜索树,但是在每一个节点上面都增加了一个存储位来表示结点的颜色,可以是红色或者是黑色,通过对任何一条从根节点到叶子节点上面的路径各个节点着色方式的限制,红黑树会自动确保没有一条路经会比其他路径的长度高出两倍,而是接近平衡的
2)红黑树最长路径是最短路径的两倍
3)每一个节点不是红色就是黑色
4)根节点是黑色的
5)如果一个节点是红色的,那么他的左右孩子的节点都是黑色的,说明红黑树没有两个连续相同的红色节点
6)对于每一个节点,从该节点到达后代的叶子结点的所有简单路径里面,均包含相同数目的黑色节点(每一条路径上都包含着相同数目的黑色节点,路径的计算必须指向空)
在红黑树中,对于每个节点,从该节点到其所有后代叶子节点的简单路径上,应包含相同数量的黑色节点,这也是红黑树的基本性质之一。
在计算路径上的黑色节点数量时,通常会包括空节点(NIL节点)因为空节点被视为黑色节点的一部分,并且它们对于保持红黑树的平衡性和性质是必要的,所以,在判断从任意节点到达后代叶子节点的所有简单路径是否包含相同数量的黑色节点时,应该将空节点(NIL节点)也计算在内
7)每一个叶子节点都是黑色的,此处的叶子节点指的是空节点
8)红黑树的最长路径:路径上节点黑红相间,一黑一红,最短路径:路径上全部是黑色节点
9)假设黑色节点总共有X个,整棵树的节点数量在[X,2X]之间
当总节点个数是X个的时候最短路径的长度:logX
当总结点个数是2X的时候最短路径长度是:logX+1,logX趋近于logN
所以最终总结:
最短路径长度为:logN
最长路径长度为:2logN
10)一个正常的二叉树,不会出现这种一条路径全部都是黑色的情况
二)红黑树的插入:
1)首先要明白,插入的节点必须是红色的节点,如果最终插入的是黑色的节点,因为我们要最终保证每一条路径上都有数目相同的黑色节点,其他路经都必须得新增黑色节点,但是此时新插入的是一个黑色节点,其他路经也没有办法新增节点呀,但是此时就不满足一个条件,两个红色节点挨在一起了,所以需要调节成合适的颜色
2)红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可以分为两步
2.1)按照二叉搜索树的规则插入新节点
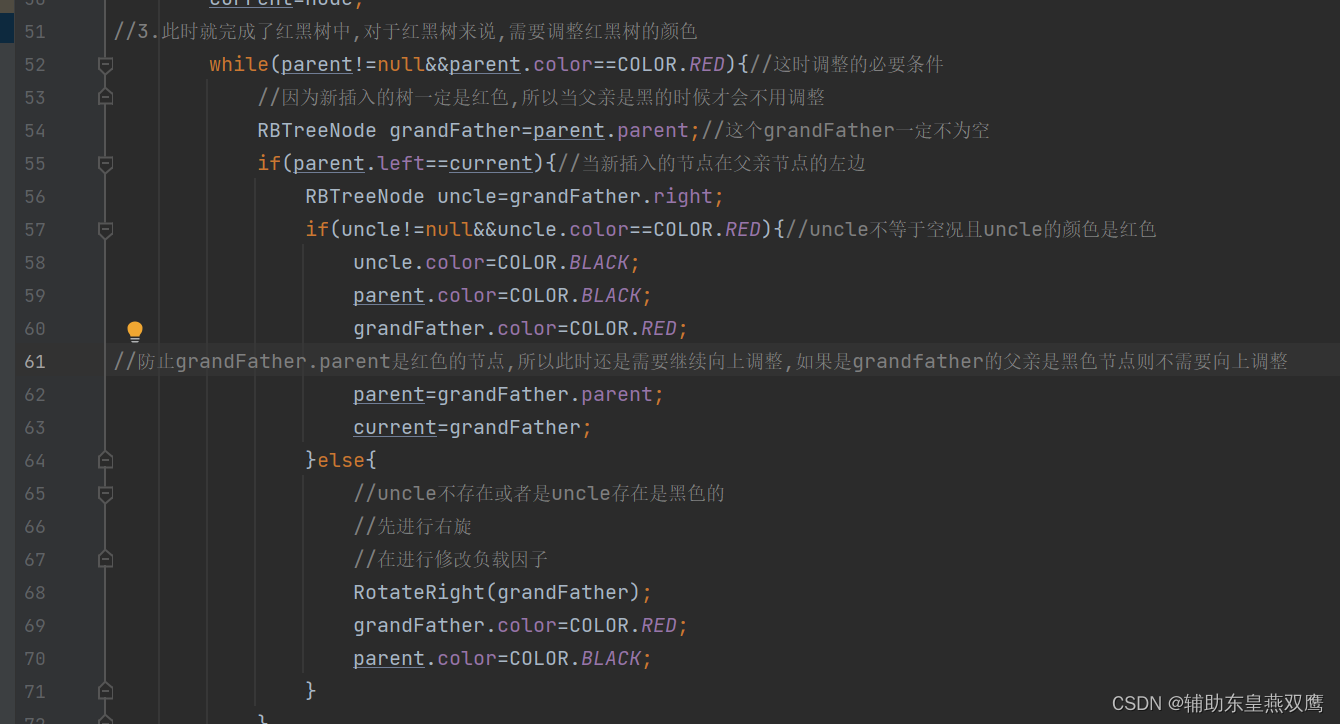
2.2)检测插入新节点之后,判断红黑树的性质是否已经遭受到了破坏,因为新节点的默认颜色是红色,因此如果双亲结点的颜色是黑色,那么其实本质上并没有违反红黑树的任何性质,那么就不需要进行调整,但是当插入的新节点的双亲结点是红色的时候,就违反了不能有连在一起的红色节点,此时需要对红黑树来分情况进行讨论:
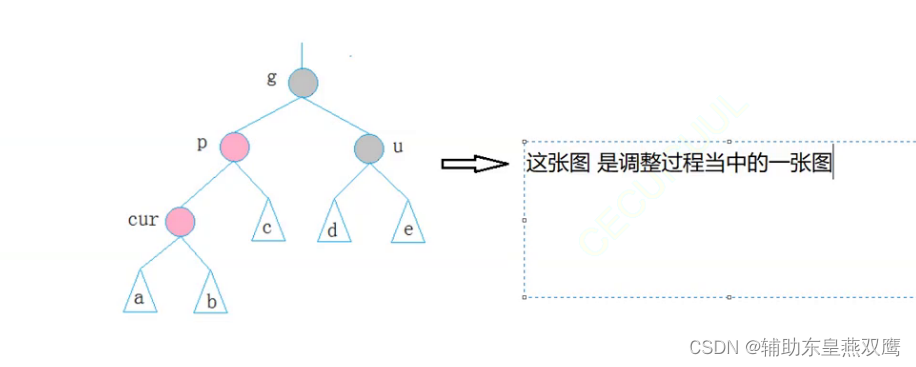
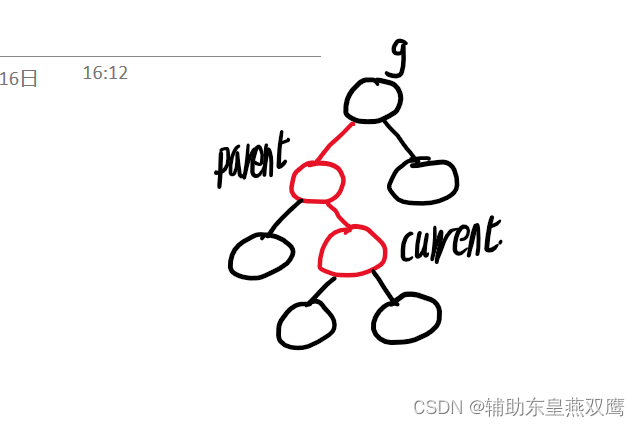
约定current为当前新插入的节点,parent为父亲节点,grandfather是祖父节点,uncle为叔叔节点
一)一共是有两种大的情况:parent是在grandfather的left节点:
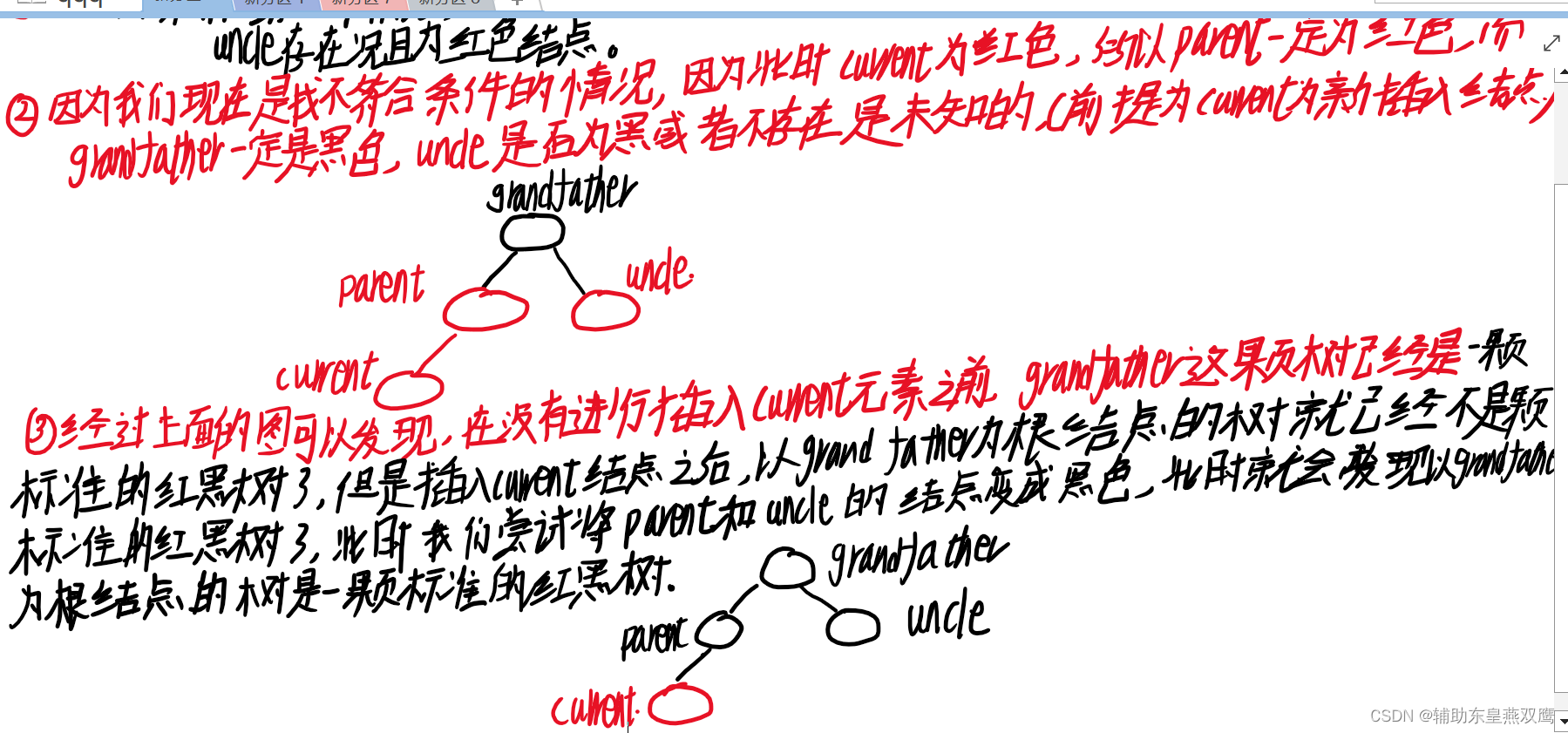
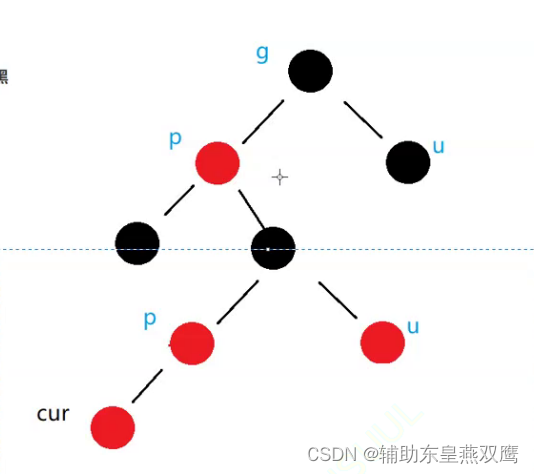
1)current为红色节点,parent是红色节点,grandfather是黑色节点,uncle存在是红色节点,下面都是默认讨论curent是parent的左子树,但是实际情况current下可能是parent的左子树,还有可能是parent的右子树;
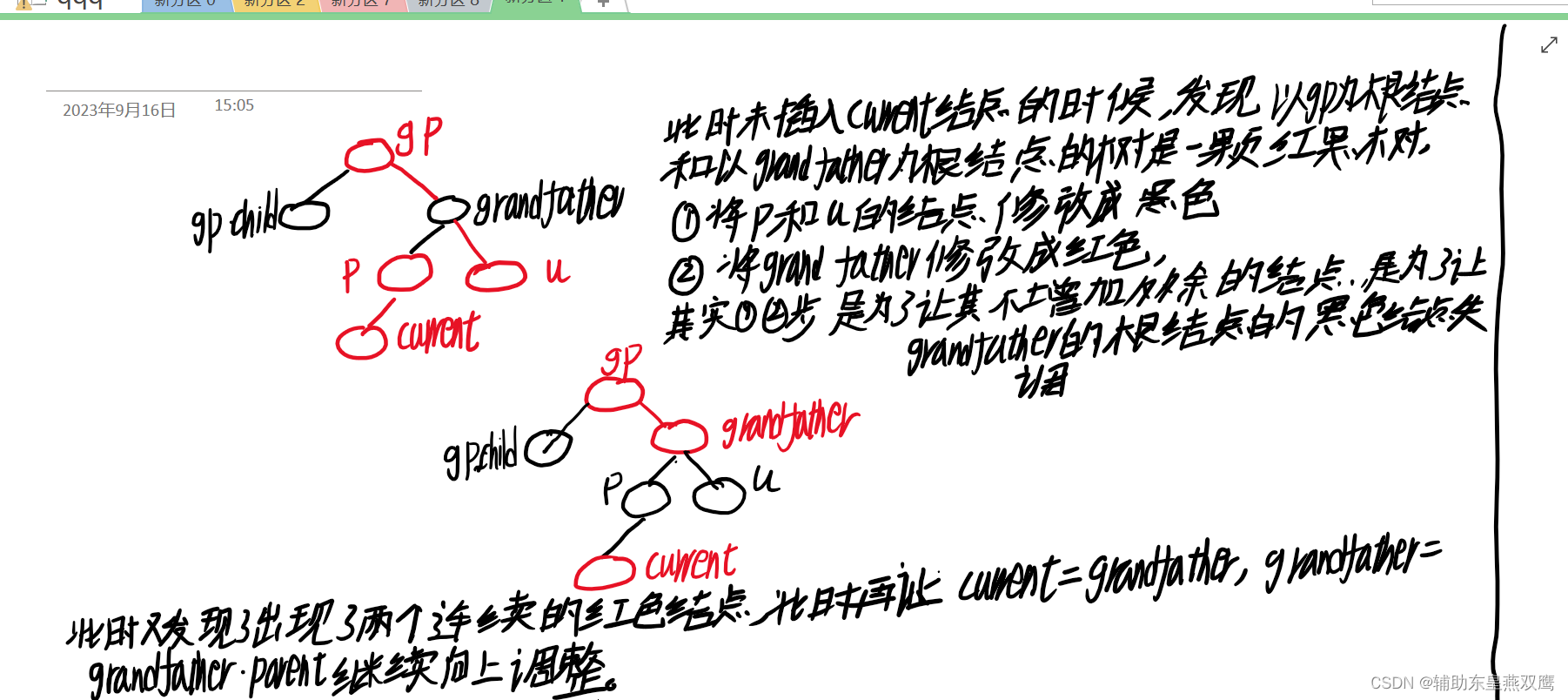
1.1)下面只是考虑到了grandfather以下的节点:发现只需要把parent节点和uncle节点变成黑色,就可以简单的满足以grandfather为根节点的树,从根节点到叶子节点的树是一颗标准的红黑树,此时gp的左子树一定是有一个黑色节点的;
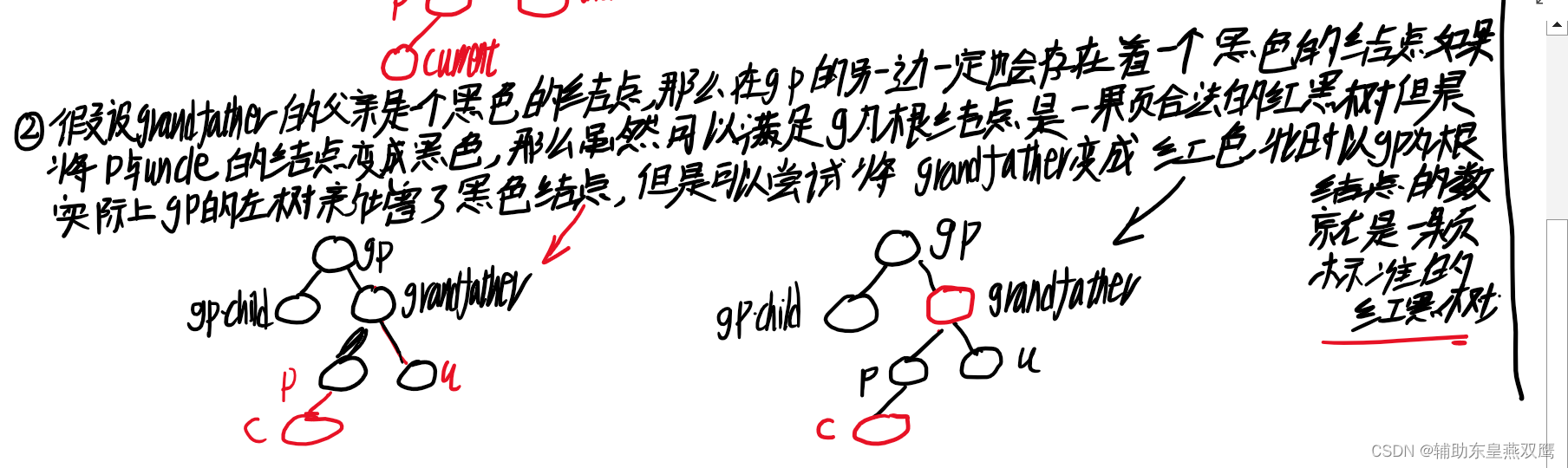
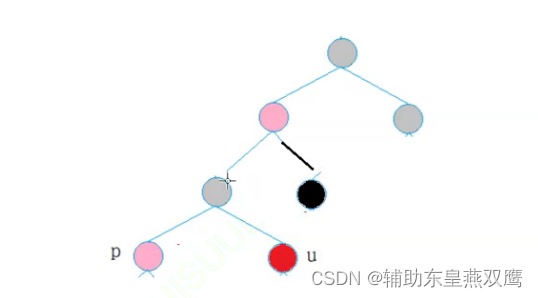
1.2)第二个横线更深一步考虑,当考虑到granfather的父亲节点的时候,当grandfather的父亲节点是黑色的时候或者是grandfather节点是红色的时候,需要再进一步分情况进行讨论:
1.3)当grandfather的父亲节点是黑色的时候说明,grandfather的另一个孩子也是黑色节点
此时如果将grandfather的这个节点的父亲节点是一个黑色的节点那么如果只是单纯的将p和u变成黑色是万万不可以的,这样只会增加黑色节点的个数
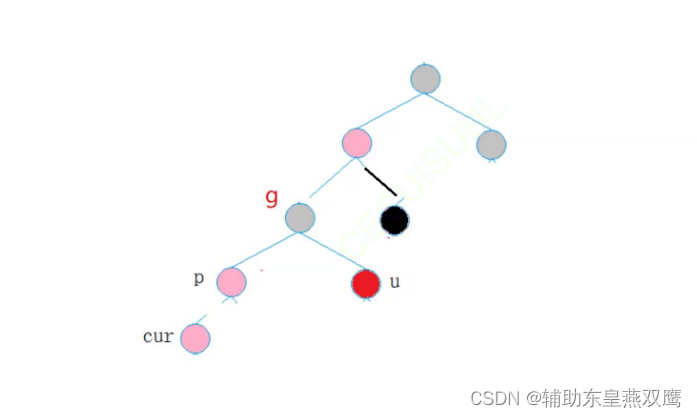
1.4)假设grandfather的父亲节点是红色,此时可以分析出gp的左孩子一定是黑色的
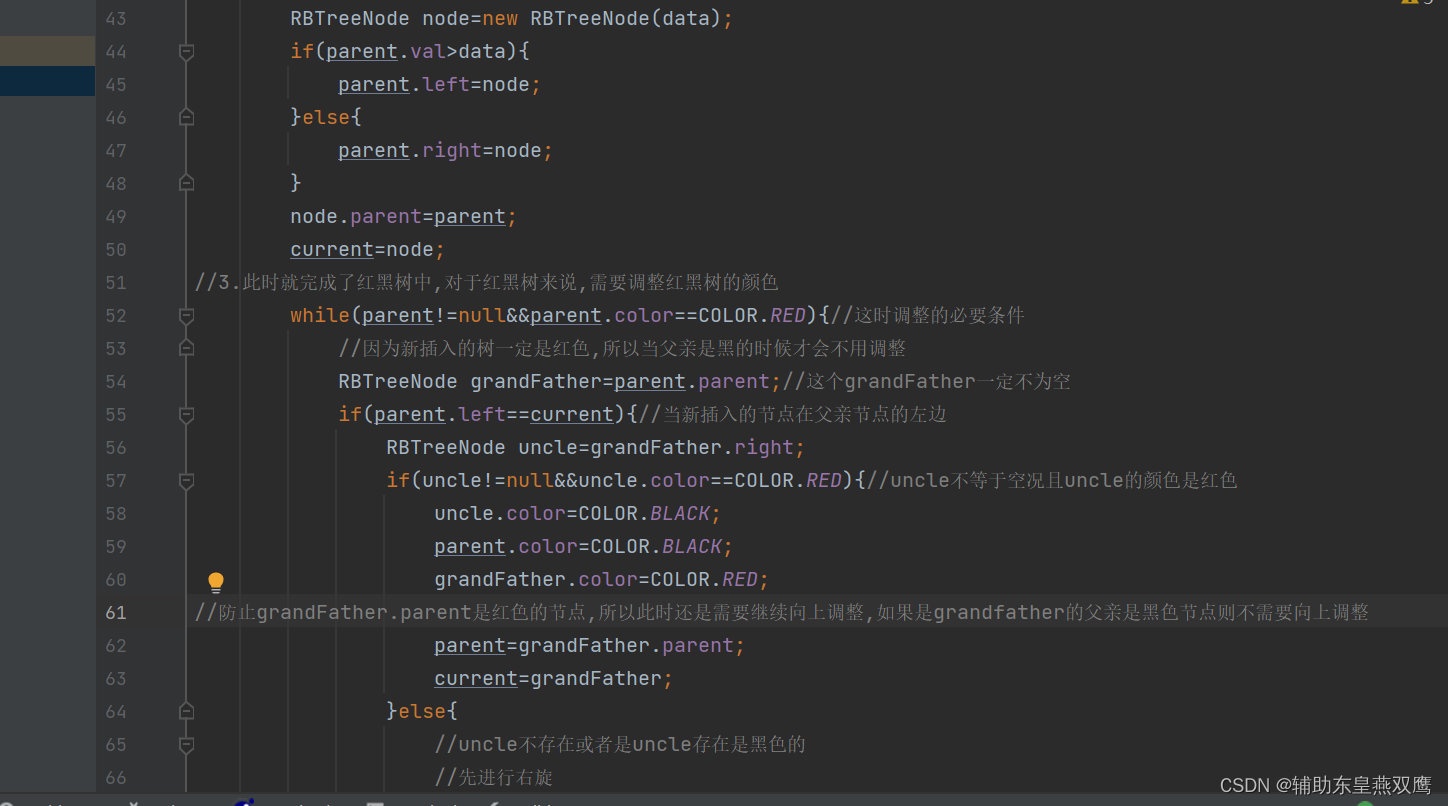
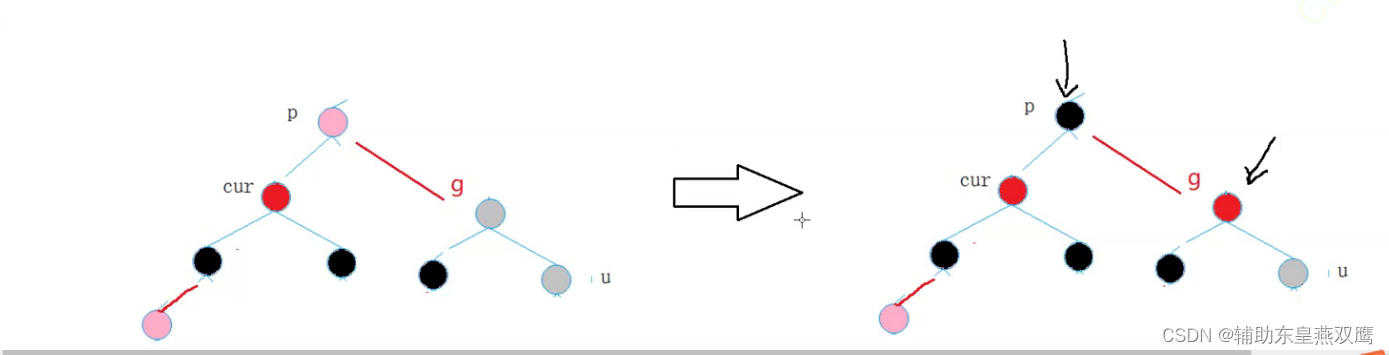
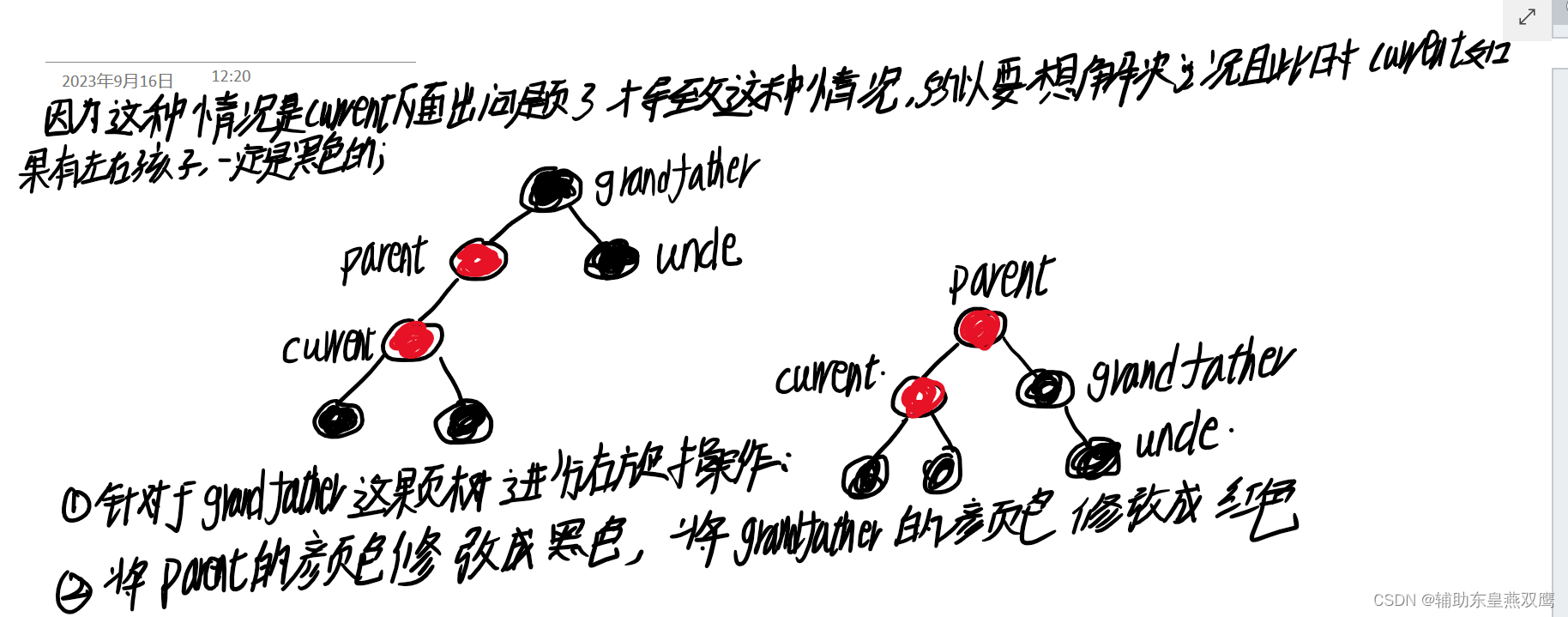
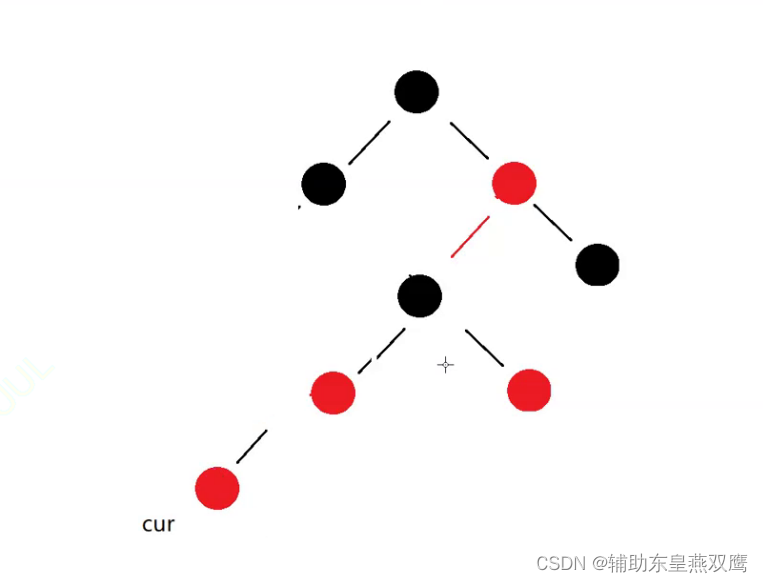
2)current为红色,parent是红色,grandfather是黑色,uncle不存在或者是uncle是黑色
此时current下面一定有子树其他节点:是再调整的过程中current变成红色的
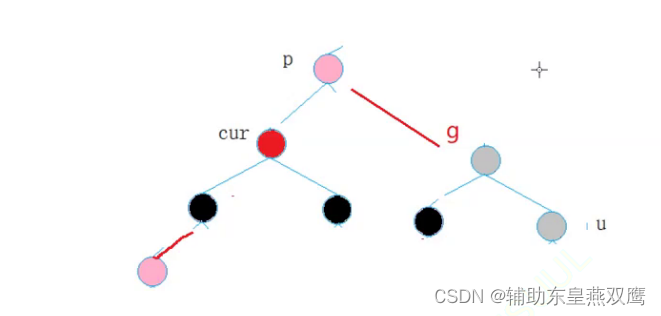
先进行右旋:
然后修改颜色:
3)current是红色,parent是红色,grandFather是黑色,uncle不存在或者uncle是黑色
二)第二种情况parent是在grandfather的right节点:
相关文章:
高阶数据结构(2)-----红黑树(未完成)
一)红黑树的基本概念和基本性质: 1)红黑树就是一种高度平衡的二叉搜索树,但是在每一个节点上面都增加了一个存储位来表示结点的颜色,可以是红色或者是黑色,通过对任何一条从根节点到叶子节点上面的路径各个节点着色方式的限制,红黑…...

[mockjs]Mock使用过程中的坑
[mockjs]Mock使用过程中的坑 现象描述原因分析解决方案修改源码处理无法识别的文件流 现象描述 mockjs在使用的过程中出现了下载文件无法正常打开的问题,但是在线上环境是正常的 console.log打印返回的response,发现是本地无法正常解析response.data 在代码中&am…...
华为云云耀云服务器L实例评测|部署前后端分离项目
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 学习测评 ✨特色专栏: MyS…...
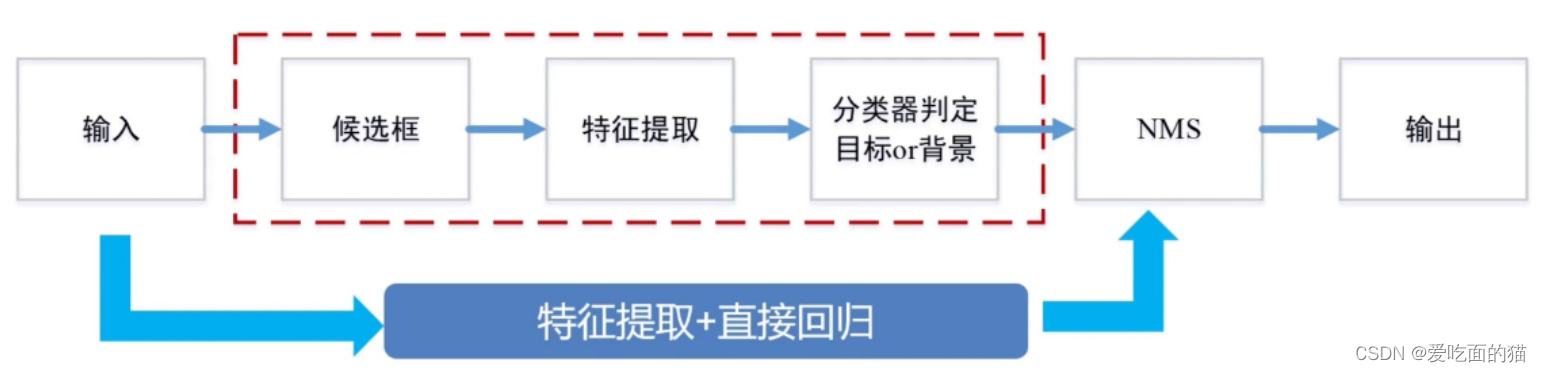
02目标检测-传统检测方法
目录 一、目标学习的检测方法变迁及对比 二、 基于传统手工特征的检测算法的定义 三、传统主要手工特征与算法 Haar特征与 人脸检测算法 - Viola-Jones(了解) HOG特征与 SVM 算法(了解)(行人检测、opencv实现) SIFT特征与SIFT算法(了解) DPM&#…...
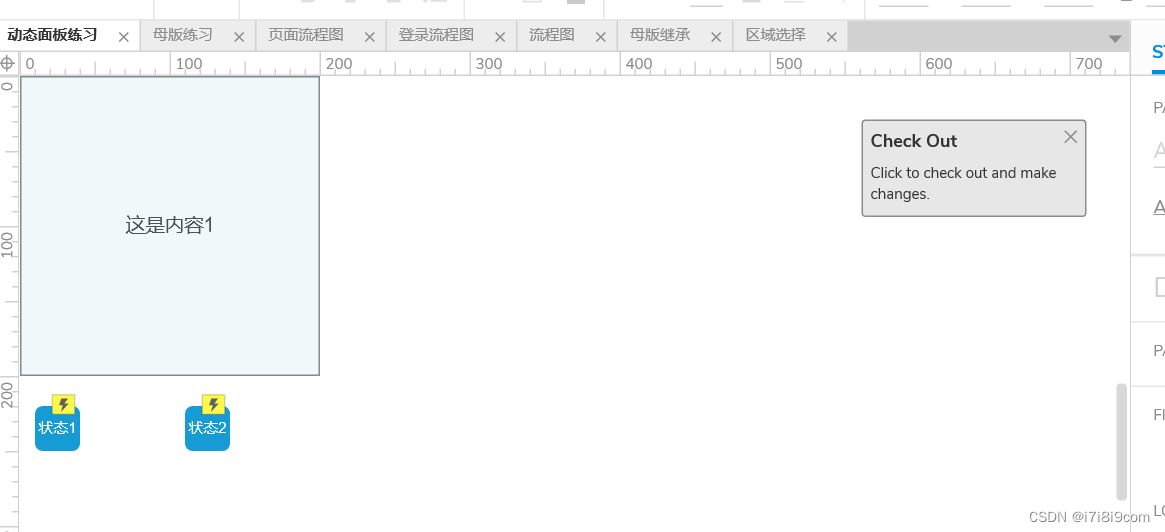
RP-母版 流程图 发布和预览 团队项目
母版 创建一个模版,可根据形态不同引用不同母版。若不想母版受页面变化影响,也可以在引用时脱离母版 创建母版: 1) 转换为母版 2)在母版页面中添加 母版拖放行为 拖放行为,在母版名称上右键, 、 任意…...
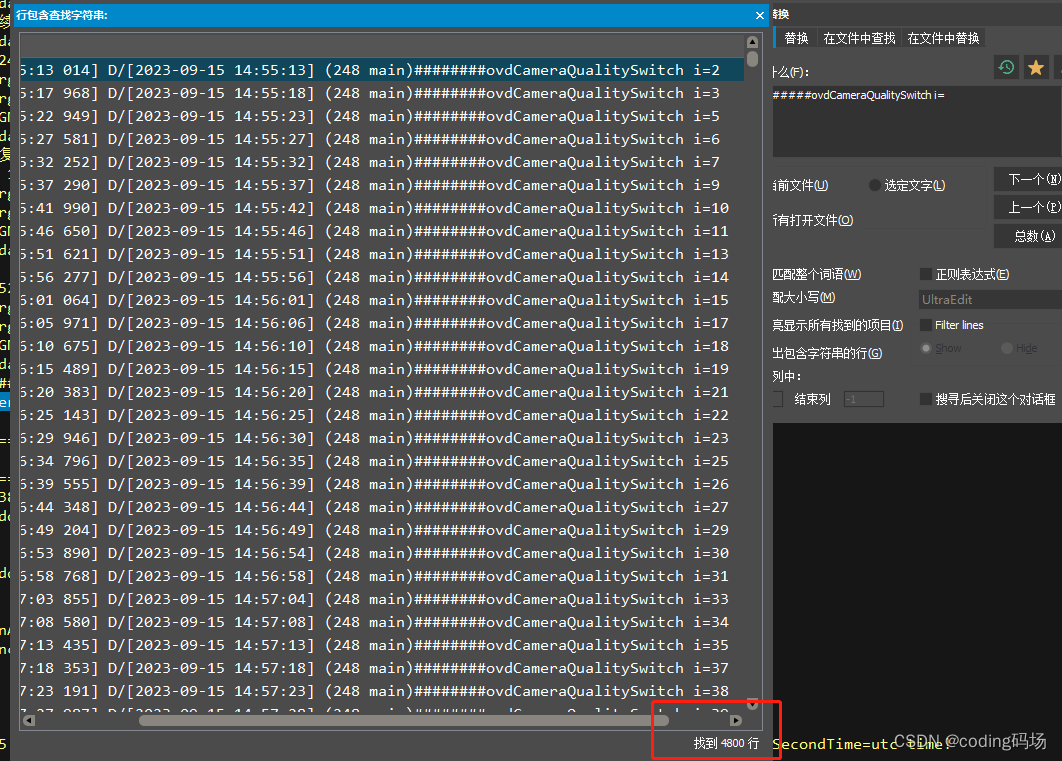
【第200篇原创文章】解决低于1%概率出现的芯片VPSS模块跑飞的问题
在发布SDK内测的时候,我们发现在切换视频分辨率的时候有低概率出现VPSS模块跑飞的情况,概率低于1%,试个两三百次,能出1~2次。切换视频分辨率这个功能在安防产品上也确实存在需求,网络带宽不大好的地方分辨率可以适当下…...

微信小程序——生命周期详解(代码解读)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
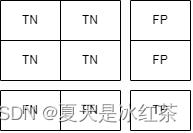
多分类中混淆矩阵的TP,TN,FN,FP计算
关于混淆矩阵,各位可以在这里了解:混淆矩阵细致理解_夏天是冰红茶的博客-CSDN博客 上一篇中我们了解了混淆矩阵,并且进行了类定义,那么在这一节中我们将要对其进行扩展,在多分类中,如何去计算TP࿰…...

Linux系统:OpenSSH7.4p升级到9.0p(服务器漏洞)
清华大学开源软件镜像站下载地址: https://mirrors.tuna.tsinghua.edu.cn/pub/OpenBSD/OpenSSH/portable/openssh-9.0p1.tar.gz 一、升级 0、安装Telnet (1)为防止安装失败,无法用ssh做远程连接,因此先安装telnet yum…...

【面试刷题】——C++的特点简单说明
C是一种通用的编程语言,具有许多强大的特点,以下是其中一些主要特点的简单说明: 面向对象编程(OOP): C支持面向对象编程,允许将数据和操作封装在类中,提高了代码的可维护性和重用性…...
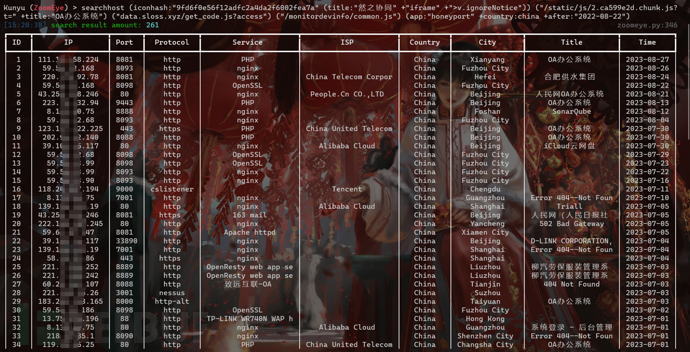
C2基础设施威胁情报对抗策略
威胁情报是指在信息安全和安全防御领域,收集、分析和解释与潜在威胁相关的信息,以便预先发现并评估可能对组织资产造成损害的潜在威胁,是一种多维度、综合性的方法,其通过信息的收集、分析和研判,帮助组织了解可能对其…...
)
差异备份详细说明(InsCode AI 创作助手)
差异备份详细说明 差异备份(Differential Backup)是一种备份策略,它与增量备份类似,但有一些关键区别。差异备份备份的是自上一次完整备份以来的所有更改数据,而不是自上一次备份以来的所有更改。这意味着差异备份文件…...

flask要点与坑
简介 Flask是一个用Python编写的Web应用程序框架,该框架简单易用、模块化、灵活性高。 该笔记主要记录Flask的关键要点和容易踩坑的地方 Flask 日志配置 Flask 中的自带logger模块(也是python自带的模块),通过简单配置可以实现…...
EasyUI combobox 实现搜索(模糊匹配)功能
很简单的一个下拉框搜索模糊匹配功能,在此记录: 1:页面实现: <select class"easyui-combobox" name"combobox" id"combobox" style"width:135px;height:25px;" headerValue"请选…...
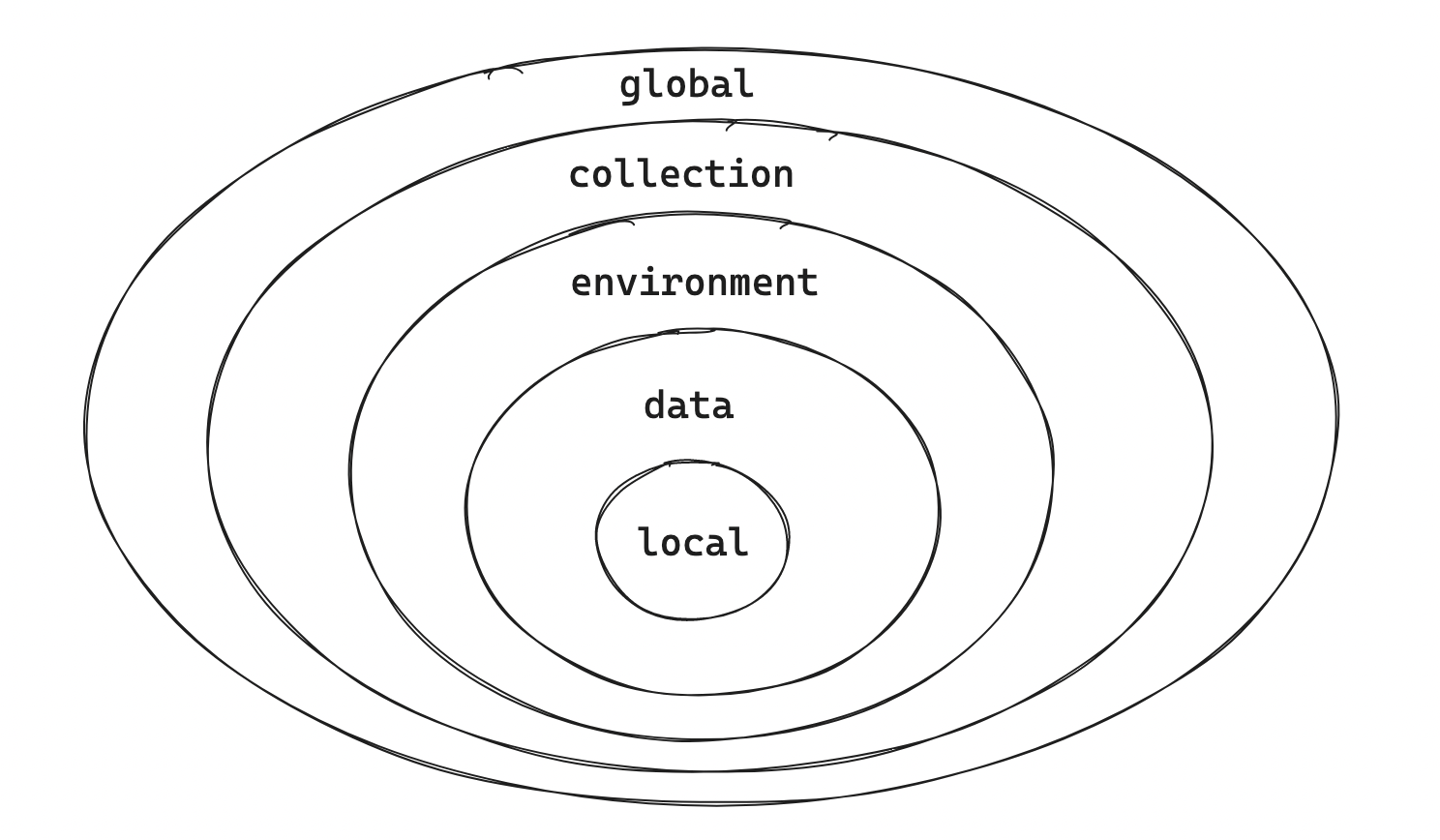
Postman的高级用法一:重新认识postman核心模块
本请求示例来自于免费天气API: 实况天气接口API开发指南 未来一天天气预报api - 天气API 关于Postman的核心模块 全局变量请求接口请求体预处理脚本 类似beforeTest,在发起请求前的预执行逻辑,通常是生成一些动态变量值 测试用例模块 测试者…...

git命令的操作
git命令操作及命令大全 1.创建一个新的本地仓库:2.添加文件到仓库:3.远程仓库操作:4.分支操作:5.git命令大全 1.创建一个新的本地仓库: 使用命令git init在本地目录中创建一个新的git仓库。 2.添加文件到仓库&#x…...
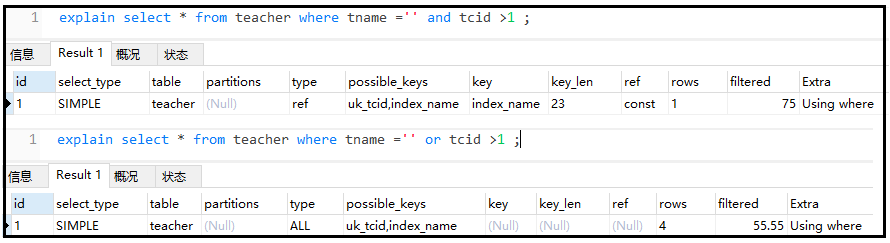
超级详细 SQL 优化大全
1、MySQL的基本架构 1)MySQL的基础架构图 左边的client可以看成是客户端,客户端有很多,像我们经常你使用的CMD黑窗口,像我们经常用于学习的WorkBench,像企业经常使用的Navicat工具,它们都是一个客户端。右…...

数据治理-数据存储和操作-数据库组织模型
数据库存储系统提供了一种将数据放入磁盘并管理和处理这些数据所需指令的封装方法,因此开发人员可以简单地使用指令来操作数据。数据库通常以3种形式进行组织:层次性、关系型和非关系型;这种归类并不是完全互斥的。一些数据库系统可以同时读写…...
IDEA最新激 20活23码
人狠话不多 大家好,最近Intelli Idea官方的校验规则进行了更新,之前已经成功激20活23的Idea可能突然无法使用了。 特地从网上整理了最新、最稳定的激20活23码分享给大家,希望可以帮助那些苦苦为寻找Idea激20活23码而劳累的朋友们。 本激23…...
flutter产物以aar形式嵌入android原生工程
以前做的项目中,flutter都是作为module嵌入原生工程中,新公司项目却是以aar形式嵌入android工程,这种优点是原生工程不必配置flutter环境也能跑了,这里记录一下简单步骤。 创建一个flutter module 通过android studio创建一个fl…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
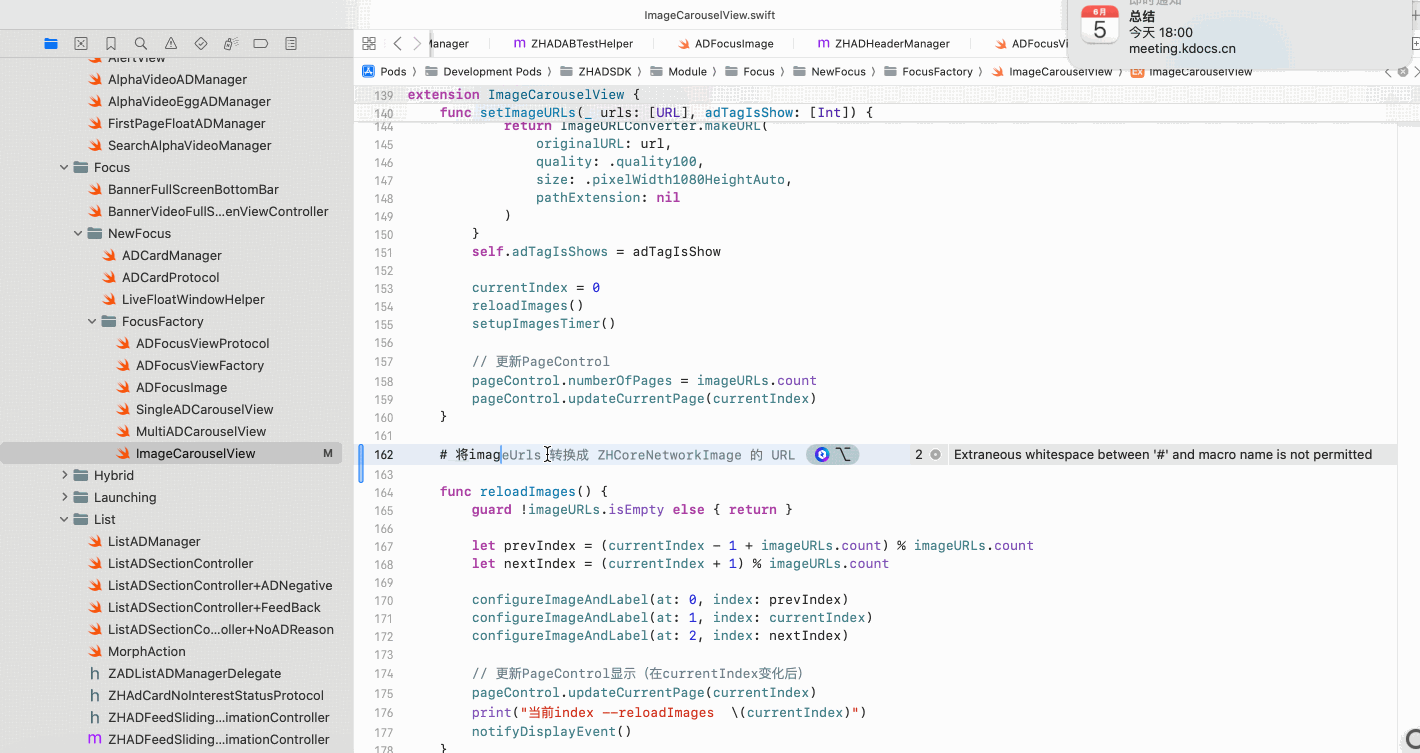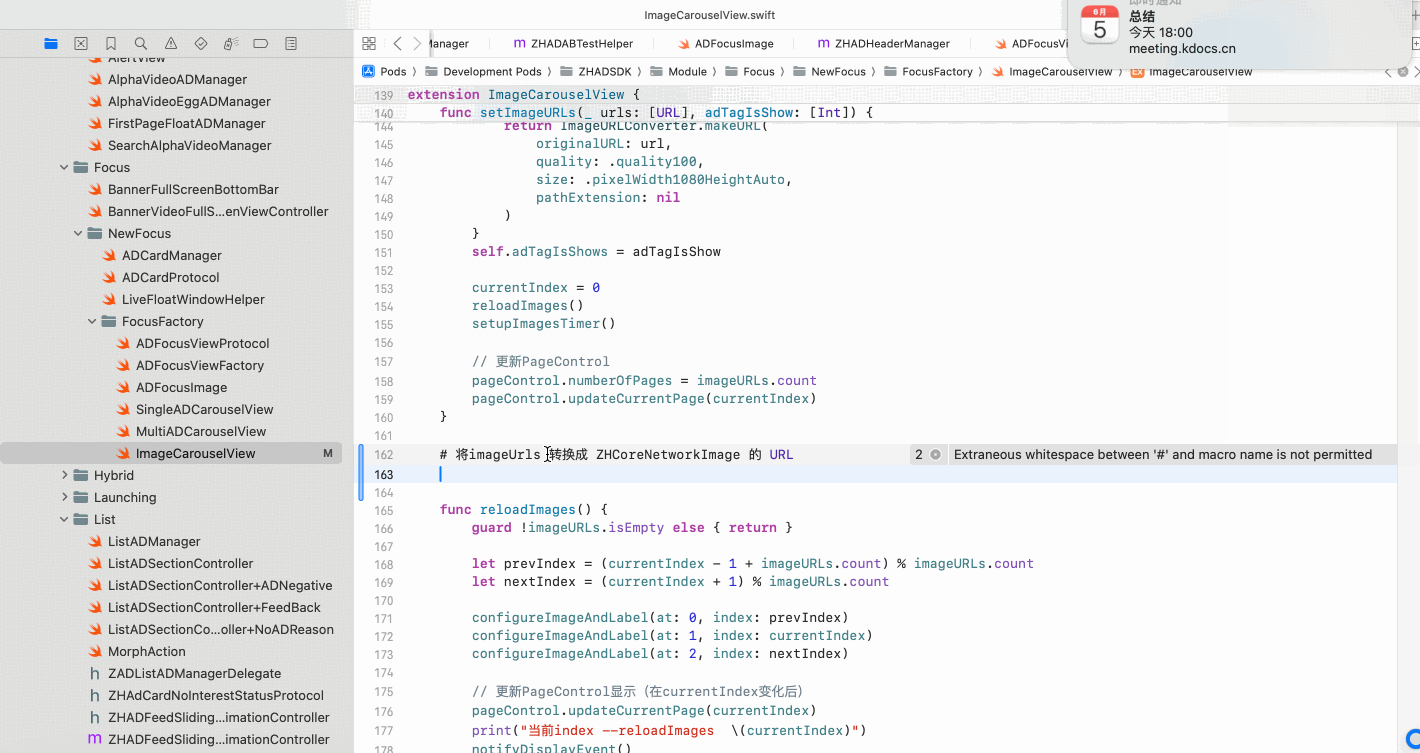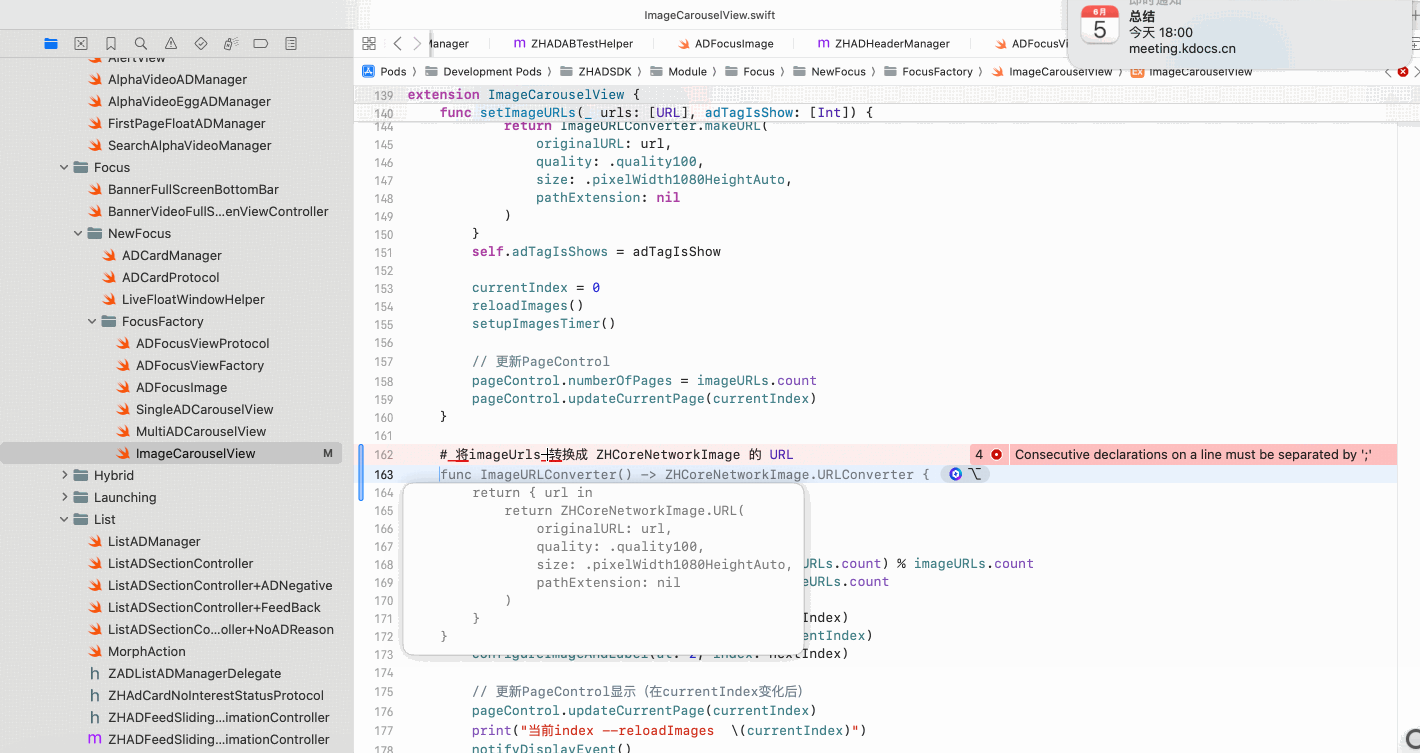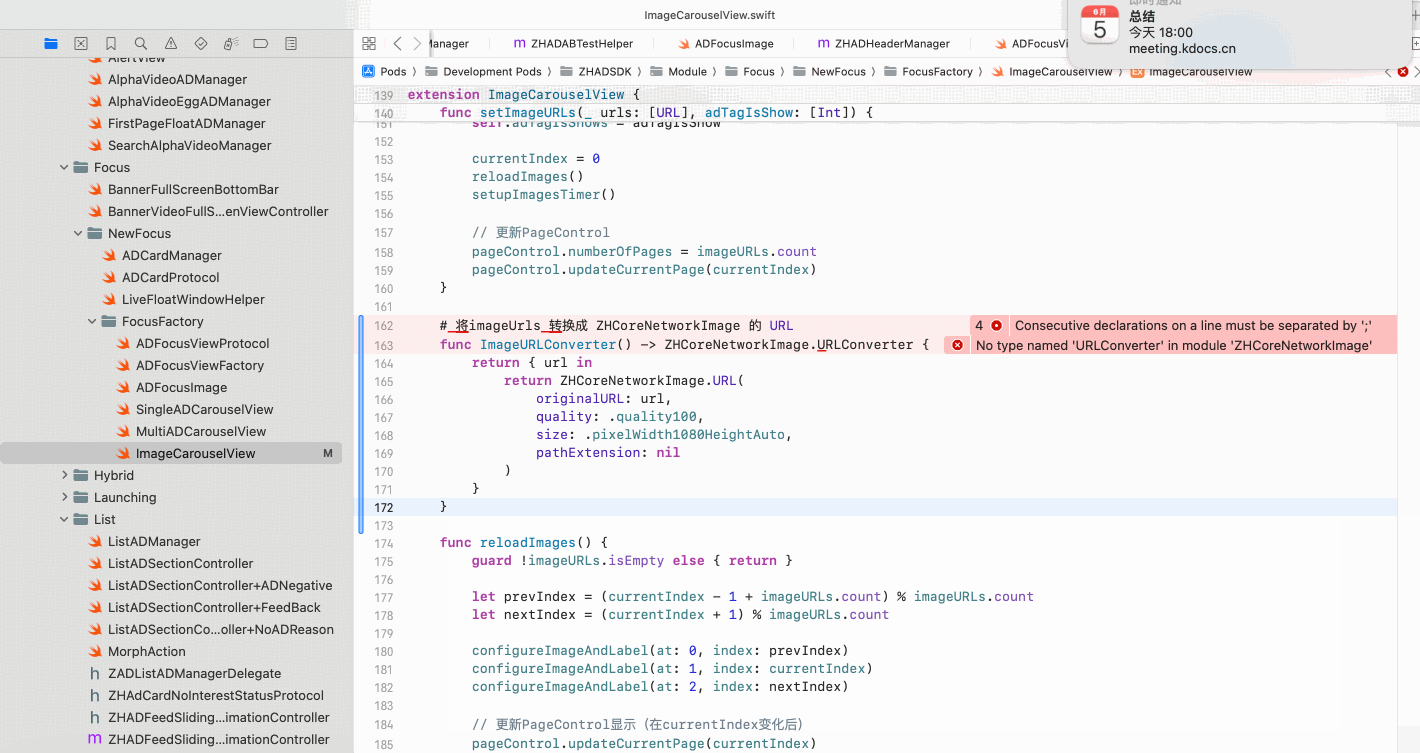
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...