Python傅立叶变换
1. 什么是傅里叶变换?
在数学中,变换技术用于将函数映射到与其原始函数空间不同的函数空间。傅里叶变换时也是一种变换技术,它可以将函数从时域空间转换到频域空间。例如以音频波为例,傅里叶变换可以根据其音符的音量和频率来表示它。
我们可以说,任何函数的傅里叶变换所执行的变换都是频率的函数。其中结果函数的大小是原始函数所包含的频率的表示。
让我们举一个信号的例子,它的时域函数如下所示:

在同一时间范围内获取另一个信号的一部分

将这两个信号的称为 A(n) 和 B(n),其中 n 是时域。因此,如果我们添加这些信号,信号的结构将如下所示:
C(n) = A(n) + B(n)

可以看到,函数的信号相加是将两个信号进行了加的操作,如果我们试图从这个相加信号 C 中提取信号 A 或 B,我们会遇到一个问题,因为 这些信号只是功率相加,和时间没有关系。也就是说相加的操作是同一时间上的功率的相加。

可以在上图中看到,频域可以很容易地突出信号之间的差异。如果希望将这些信号转换回时域,我们可以使用傅里叶逆变换。
2. numpy.fft与scipy.fft
Python的numpy和scipy模块提供了数学中所需的所有转换技术,所以可以直接使用它。
下面的例子都是用的scipy,但是实际使用中如果能不用scipy尽量不用,毕竟少用一个库就少一些部署上的麻烦。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
制作正弦波
# sample points
N = 1200# sample spacing
T = 1.0 / 1600.0x = np.linspace(0.0, N*T, N, endpoint=False)
sum = np.sin(50.0 * 2.0 * np.pi*x) + 0.5*np.sin(80.0 * 2.0 * np.pi*x)plt.plot(sum)
plt.title('Sine wave')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.grid(True, which='both')
plt.show()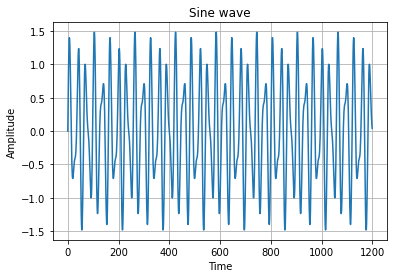
上面的输出中,可以看到使用 NumPy 生成的正弦波,现在可以使用 scipy 库的 FFT 模块对其进行转换。
sumf = fft(sum)
xf = fftfreq(N, T)[:N//2]
plt.ylabel('frequency')
plt.xlabel('sample')
plt.title("FFT of sum of two sines")
plt.plot(xf, 2.0/N * np.abs(sumf[0:N//2]))
plt.show()fft输出的结果是复数,其中实部表示频率,虚部表示相机,如果只关心频率,取绝对值即可。
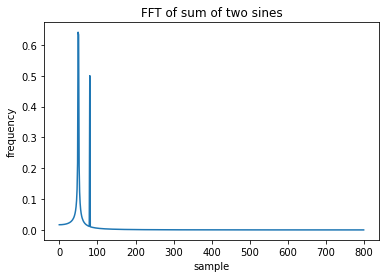
现在可以清楚地看到各种波的频率是多少,作为时域的函数形成的时这些并不明显,只有在频域表示时才能清楚的看到这些区别。
参考文献
主要内容来自下文,内容略有增加
神经网络与傅立叶变换有何关系?
相关文章:

Python傅立叶变换
1. 什么是傅里叶变换? 在数学中,变换技术用于将函数映射到与其原始函数空间不同的函数空间。傅里叶变换时也是一种变换技术,它可以将函数从时域空间转换到频域空间。例如以音频波为例,傅里叶变换可以根据其音符的音量和频率来表示…...

MATLAB向量化编程基础精讲教程
向量化编程是MATLAB中一种重要的编程技术,通过使用向量和矩阵运算代替循环,可以提高代码的执行效率和可读性。本文将介绍MATLAB向量化编程的基础知识,并提供多个案例代码,帮助读者理解和应用向量化编程。 一、向量化编程基础知识…...

【非对称加密算法】RSA算法
一、非对称加密算法 非对称加密算法使用了两个不同的密钥:公钥和私钥。公钥是公开的,可以被任何人使用,而私钥是只有特定的人能够使用的。这种算法的加密和解密过程使用不同的密钥,因此称为非对称加密算法。 在非对称加密算法中…...

【滑动窗口】438. 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词 滑动窗口解法 创建两个Map 一个记录实际需要的有效字符 另一个记录窗口内的有效字符个数初始化need每次遍历一个字符 判断是不是有效字符 如果是 更新window 另外判断window中有效字符的个数是不是等于need中有效字符的个数 如果是更新valid…...

【PowerQuery】Excel 一分钟以内刷新PowerQuery数据
当需要进行刷新的周期如果小于一分钟,采用数据自动刷新就无法实现自动刷新的目标。那就没有办法了吗?当然不是,这里就是使用VBA来实现自动刷新。这里实现VBA刷新的第一步就是将当前的Excel 保存为带有宏的Excel 文件,如果不带宏则无法运行带有宏代码的Excel文件,保存过程如…...
【C语言】用冒泡排序实现my_qsort
大家好,我是苏貝,本篇博客带大家了解如何用冒泡排序实现my_qsort,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一. 前言二. 冒泡排序三. 4个参数3.1 第一个参数void* base3.2 第二个参数…...

【css】深入理解flex属性
参考文章: 深入理解Flex属性 flex弹性布局教程-05-项目属性flex-shrink flex:flex-grow flex-shrink flex-basis flex:0 1 0 如何计算flex布局,有flex-shrink和flex-grow的情况下,每个元素的大小 flex-grow生效公式如…...
前端项目开发流程
一 参加需求对称(评审)会议 时间:在产品设计完成以后,进入正式的开发流程之前 组织者:产品&项目经理 目的:统一大家对产品的认识,及时发现产品设计缺陷,尽可能降低后续修改需求的频率 参与者ÿ…...

MybatisPlus逆向工程入门指南:让你的开发更高效、更简洁、更优雅
学会了,可以看看这篇文章:更新中~ 正向工程:先创建Java实体类,由框架负责根据实体类生成数据库表。Hibernate是支持正向工程的。 逆向工程:先创建数据库表,由框架负责根据数据库表,反向生成如下…...

通用商城项目(下)
记录一些踩坑的地方,以及理顺一些思路。 通过管理系统页面,完成商品属性分组和商品属性(基本属性)关联维护 属性表 与 属性组表 的功能完善:显示属性组与属性表的一对多关系 前端 1. 引入组件,是否显示使…...
k8s集群使用ingress转发grafana服务
文章目录 前言一、思路二、grafana准备1. grafana-configmap.yaml2. grafana.yaml 三、ingress准备1. ingress.yaml2. grafana-externalname.yaml3. ingress-nginx-controller 四、 本机host文件准备五、访问测试 前言 在k8s集群中,使用ingress服务转发grafana的页…...

MongoDB的备份和恢复
工具 mongodump 和 mongorestore是MongoDB自带的备份恢复工具。 参考文章 ## https://blog.csdn.net/GUDUzhongliang/article/details/131915625## https://blog.csdn.net/mingongge/article/details/130695422 备份 mongodump 参数 -h, --host<hostname> …...

Pytorch学习笔记(GPU训练)
GUP训练 配置pytorch的gup版本主要是在网络模型、输入和标记的数据、损失函数 方式一 直接.cuda()调用,在原有的模型训练代码中的网络模型、输入和标记的数据、损失函数部分直接调用即可 方式二 事先定义好设备device,然后直接.to(device)调用,在原…...
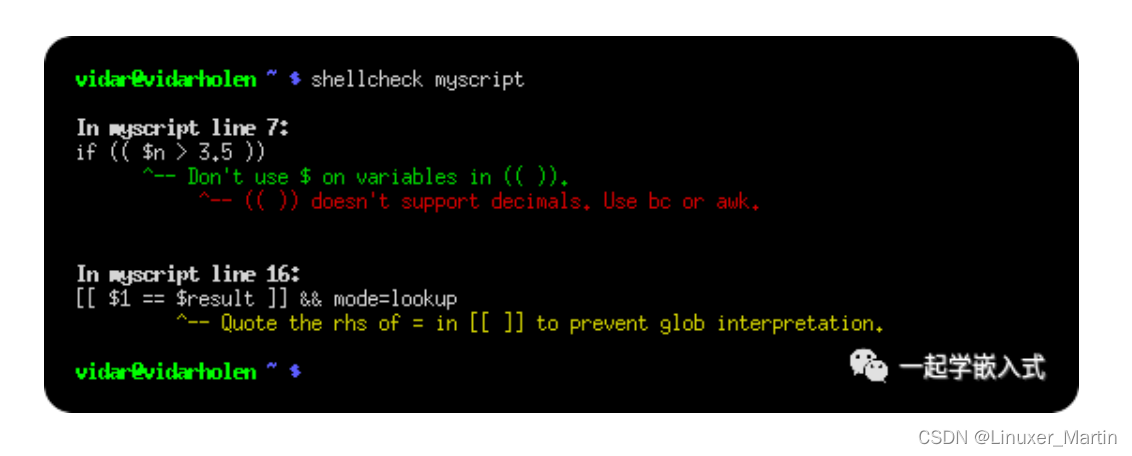
一款开源的shell脚本分析工具
大家好,今天分享一款开源工具--shellcheck。 shellcheck 简介 今天发现的一款神器,如果你日常会接触到shell脚本,或者说自己需要写一些shell脚本,那么强烈建议你用下这个工具。 shellcheck一个静态的shell脚本分析工具…...

HTML <video> 标签
实例 一段简单的 HTML5 视频: <video src="movie.ogg" controls="controls"> 您的浏览器不支持 video 标签。 </video>定义和用法 <video> 标签定义视频,比如电影片段或其他视频流。 浏览器支持 元素ChromeIEFirefoxSafariOpera&l…...
mac 本地运行 http-proxy-middleware ,请求超时
const http require(http)"/customer": {target: "http://10.10.111.192:8080/",// target: "http://user.jinfu.baohan.com/",changeOrigin: true, // 是否启用跨域// 解决mac 代理超时问题headers: {Connection: "keep-alive"},// …...

【Effective Python】读书笔记-05类与接口
1. 让组合起来的类来实现多层结构,不用使用嵌套的内置类型 2. 让简单的接口接收函数,而不是类的实例 from collections import defaultdictcurrent {a: 1,b: 2,c: 3, }add_to_current {f: 4,e: 5, }def increment():count 0def missing():nonlocal …...

【办公自动化】用Python在Excel中查找并替换数据(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
python学习随笔3
range的使用 range()在python很常用,可以进行初始化和遍历等。 # range(st,ed) # [st, ed)# range(st,ed,step) # range(st, ed, step) i,i step, i 2 * step ... () < ed切片 跟range类似。 ll[st:ed:step]容器 元组 python中的元组中内容不可以进行更…...

《TCP/IP网络编程》阅读笔记--epoll的使用
1--epoll的优点 select()的缺点: ① 调用 select() 函数后针对所有文件描述符的循环语句; ② 调用 select() 函数时需要向操作系统传递监视对象信息; epoll()的优点: ① 无需编写以监视状态变化为目的的针对所有文件描述符的循环语…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
