[USACO03FALL / HAOI2006] 受欢迎的牛 G(C++,强连通分量)
题目背景
本题测试数据已修复。
题目描述
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 AAA 喜欢 BBB,BBB 喜欢 CCC,那么 AAA 也喜欢 CCC。牛栏里共有 NNN 头奶牛,给定一些奶牛之间的爱慕关系,请你算出有多少头奶牛可以当明星。
输入格式
第一行:两个用空格分开的整数:NNN 和 MMM。
接下来 MMM 行:每行两个用空格分开的整数:AAA 和 BBB,表示 AAA 喜欢 BBB。
输出格式
一行单独一个整数,表示明星奶牛的数量。
样例 #1
样例输入 #1
3 3
1 2
2 1
2 3
样例输出 #1
1
提示
只有 333 号奶牛可以做明星。
【数据范围】
对于 10%10\%10% 的数据,N≤20N\le20N≤20,M≤50M\le50M≤50。
对于 30%30\%30% 的数据,N≤103N\le10^3N≤103,M≤2×104M\le2\times 10^4M≤2×104。
对于 70%70\%70% 的数据,N≤5×103N\le5\times 10^3N≤5×103,M≤5×104M\le5\times 10^4M≤5×104。
对于 100%100\%100% 的数据,1≤N≤1041\le N\le10^41≤N≤104,1≤M≤5×1041\le M\le5\times 10^41≤M≤5×104。
解题思路:
根据题意中的“喜欢可以传递”,在一个爱慕环中的奶牛可以缩成一头奶牛
因为环中任何一头奶牛所喜欢的也被环中其他的奶牛喜欢
喜欢环中任何一头奶牛也会喜欢环中所有的奶牛
采用tarjan缩点,生成一张新图,图中的所有奶牛都是“单相思”
只有图中出度为000的节点可能是明星奶牛
因为“单相思”不会得到回应,也就不会符合“被所有奶牛喜欢”这一条件
但是如果有多个出度为000的节点,那么就不存在明星奶牛,因为出度为000的奶牛不会互相喜欢
AC代码如下
#include <iostream>
#include <string.h>
#include <queue>
using namespace std;
const int max_n = 1e4;
const int max_m = 5e4;int n, m, u, v;
//链式前向星
int head[max_n + 1];
int tot = -1;
struct edge { int v, next; }edges[max_m];
//tarjan缩点
int timeclock = 0, dfn[max_n + 1], low[max_n + 1];
int in_stack[max_n + 1], stack[max_n], rsp = -1;
//新图
int belong[max_n + 1], power[max_n + 1], cnt = 0;
int out[max_n + 1];//入度void add_edge(int u, int v) {edges[++tot] = { v, head[u] }; head[u] = tot;
}void tarjan(int s) {dfn[s] = low[s] = ++timeclock;stack[++rsp] = s;in_stack[s] = 1;for (int i = head[s]; i != -1; i = edges[i].next) {int v = edges[i].v;if (!dfn[v]) {tarjan(v);low[s] = min(low[s], low[v]);}else if (in_stack[v]) {low[s] = min(low[s], low[v]);}}if (dfn[s] == low[s]) {cnt++;while (stack[rsp + 1] != s) {belong[stack[rsp]] = cnt;power[cnt]++;//记录合并节点的数量in_stack[stack[rsp]] = 0;rsp--;}}
}int main() {memset(head + 1, -1, sizeof(int) * max_n);cin >> n >> m;for (int i = 0; i < m; i++) {cin >> u >> v;add_edge(u, v);}for (int i = 1; i <= n; i++) {if (!dfn[i]) {tarjan(i);}}for (int i = 1; i <= n; i++) {for (int j = head[i]; j != -1; j = edges[j].next) {int v = edges[j].v;//出度计数if (belong[i] != belong[v]) {out[belong[i]]++;}}}int ans = 0, find = 0;for (int i = 1; i <= cnt; i++) {if (!out[i]) {if (find) {cout << 0 << endl;return 0;}else {find++;ans = i;}}}cout << power[ans] << endl;return 0;
}相关文章:
)
[USACO03FALL / HAOI2006] 受欢迎的牛 G(C++,强连通分量)
题目背景 本题测试数据已修复。 题目描述 每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 AAA 喜欢 BBB,BBB 喜欢 CCC,那么…...

Vue 动态路由接口数据结构化为符合VueRouter的声明结构及菜单导航结构、动态路由懒加载方法
Vue 动态路由接口数据结构化为符合VueRouter的声明结构及菜单导航结构、动态路由懒加载方法 实现目标 项目打包代码实现按需分割路由懒加载按需打包,排除引入子组件的冗余打包(仅处理打包冗余现象,不影响生产部署)解决路由懒加载…...
Python----------字符串
1.转义字符 注:转义字符放在你所想效果字符前 2.原始字符串 print(r"D:\three\two\one\now") ->D:\three\two\one\now注: 在使用原始字符串时,转义字符不再有效,只能当作原始的字符,每个字符都没有特殊…...
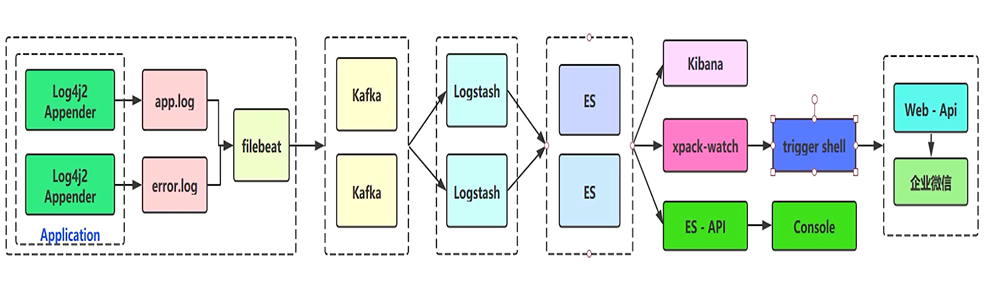
日志收集笔记(架构设计、Log4j2项目初始化、Lombok)
1 架构设计 ELK 技术栈架构设计图: 从左往右看, Beats:主要是使用 Filebeat,用于收集日志,将收集后的日志数据发送给 Kafka,充当 Kafka 的生产者Kafka:高性能消息队列,主要起缓冲…...
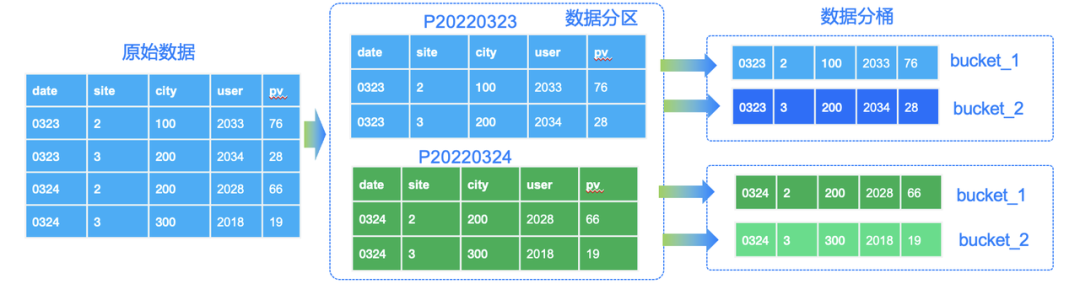
一文教你玩转 Apache Doris 分区分桶新功能|新版本揭秘
数据分片(Sharding)是分布式数据库分而治之 (Divide And Conquer) 这一设计思想的体现。过去的单机数据库在大数据量下往往面临存储和 IO 的限制,而分布式数据库则通过数据划分的规则,将数据打散分布至不同的机器或节点上…...
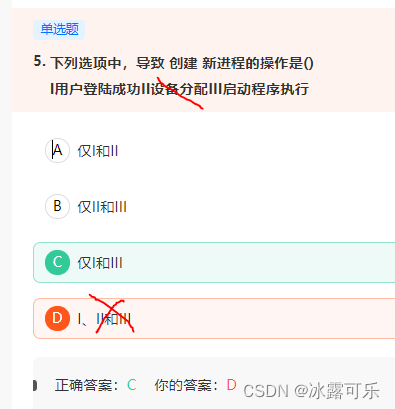
数据挖掘,计算机网络、操作系统刷题笔记54
数据挖掘,计算机网络、操作系统刷题笔记54 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,orac…...
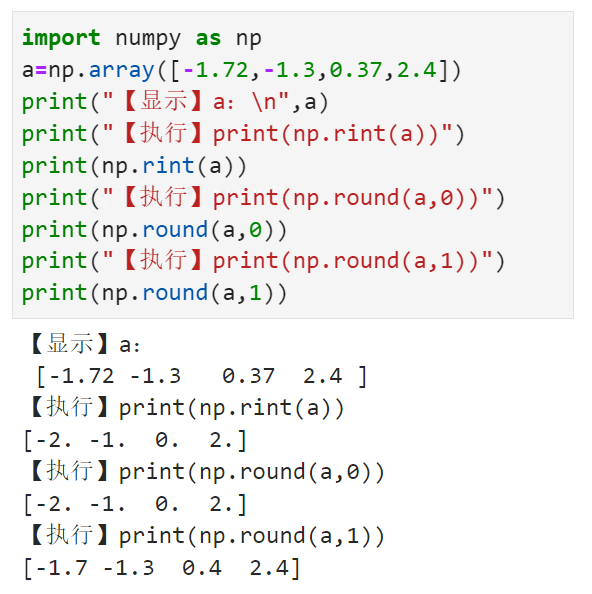
将数组中的每个元素四舍五入到指定的精度numpy.rint()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 将数组中的每个元素 四舍五入到指定的精度 numpy.rint() 选择题 请问np.rint(a)的输出结果是? import numpy as np anp.array([-1.72,-1.3,0.37,2.4]) print("【显示】a:\n…...
类漏洞详解及预防)
Web安全之服务器端请求伪造(SSRF)类漏洞详解及预防
如何理解服务器端请求伪造(SSRF)类漏洞当服务器向用户提交的未被严格校验的URL发起请求的时候,就有可能会发生服务器端请求伪造(SSRF,即Server-Side Request Forgery)攻击。SSRF是由攻击者构造恶意请求URL&…...

LeetCode:239. 滑动窗口最大值
239. 滑动窗口最大值 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1: 输入:nums [1,3,-…...
)
JS 函数参数(动态参数、剩余参数)
需求:求和函数 传入不同实参 求和出来1.动态参数 arguments 只存在于函数内function getSum() {//arguments 获取传递的所有参数 是一个伪数组let num 0for(let i0;i<arguments.length;i){num arguments[i]}return num}//调用console.log(getSum(1,2,3))consol…...
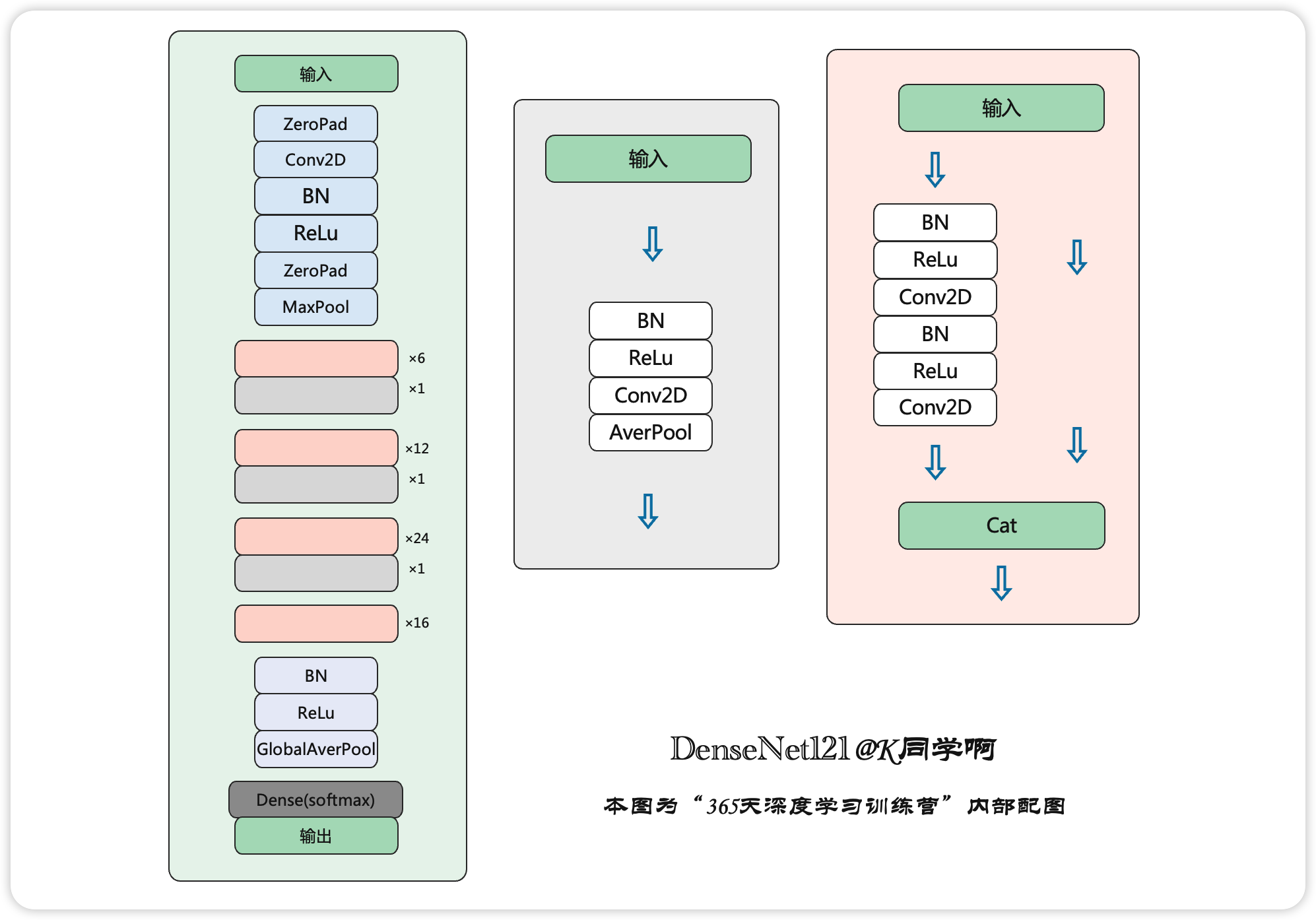
365天深度学习训练营-第J3周:DenseNet算法实战与解析
目录 一、前言 二、论文解读 1、DenseNet的优势 2、设计理念 3、网络结构 4、与其他算法进行对比 三、代码复现 1、使用Pytorch实现DenseNet 2、使用Tensorflow实现DenseNet网络 四、分析总结 一、前言 🍨 本文为🔗365天深度学习训练营 中的学习…...

Parisland NFT 作品集
该作品集用来自 Parisland 体验,共包含 11 个 NFT 资产,把你的土地装扮成一个眼花缭乱的热带天堂吧! 登上芭黎丝的爱情船和戴上豪华的螺旋爱情戒指,成为她在数位世界举办的真人秀的一部分吧!该系列还包含两个传奇级别的…...

uniapp: 基础开发官网文档
1、uniapp官网文档:https://uniapp.dcloud.net.cn/component/2、uView跨端UI组件库:http://v1.uviewui.com/components/intro.html3、lunch-request(类似axios的请求库):https://www.quanzhan.co/luch-request/handboo…...

mybatis中配置连接池的原理介绍分析
1.连接池:我们在实际开发中都会使用连接池。因为它可以减少我们获取连接所消耗的时间。2、mybatis中的连接池mybatis连接池提供了3种方式的配置:配置的位置:主配置文件SqlMapConfig.xml中的dataSource标签,type属性就是表示采用何…...
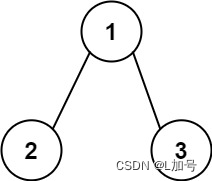
二叉树——路径总和
路径总和 链接 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点…...

WebDAV之π-Disk派盘+文件管理器
文件管理器 支持WebDAV方式连接π-Disk派盘。 推荐一款iOS上的免费文件管理器新秀。 文件管理器这是一款功能强大的文件管理工具,支持zip,rar,7z等压缩包的解压和压缩,支持小说,漫画,视频下载及播,极大提升日常办公,娱乐,文件管理的工作效率,使得文档的归档和管理随心…...

form表单单输入框回车提交事件处理
问题 form表单中如果只有一个输入框,在输入时按Enter回车键会出发默认事件自动提交表单,该交互是同步发生的,会导致页面刷新。 解决思路 有三种解决思路: 1. 增加input输入框的数量 如果form表单中不止一个input输入框&#…...
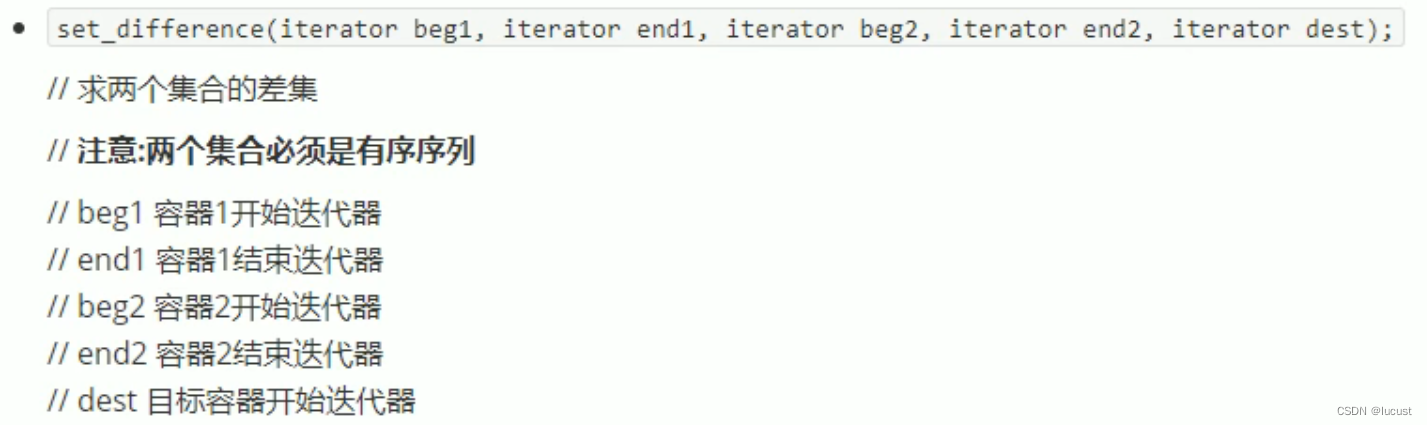
c++常用stl算法
1、头文件 这些算法通常包含在头文件<algorithm> <functional> <numeric>中。 2、常用遍历算法 for_each(v.begin(),v.end(), 元素处理函数/仿函数) 注意:在使用transform转存时,目标容器需要提取开辟合适的空间。 void printfunc(…...
非对称密钥PKCS#1和PKCS#8格式互相转换(Java)
目录一、序言二、代码示例1、Maven依赖2、工具类封装三、测试用例1、密钥文件2、公私钥PKCS1和PKCS8格式互相转换一、序言 之前在 《前后端RSA互相加解密、加签验签、密钥对生成》 中提到过PKCS#1格式和PKCS#8格式密钥的区别以及如何生成密钥。实际有些场景中有可能也会涉及到…...

java获取当前时间的方法:LocalDateTime、Date、Calendar,以及三者的比较
文章目录前言一、LocalDateTime1.1 获取当前时间LocalDate.now()1.2 获取当前时间的年、月、日、时分秒localDateTime.getYear()……1.3 给LocalDateTime赋值LocalDateTime.of()1.4 时间与字符串相互转换LocalDateTime.parse()1.5 时间运算——加上对应时间LocalDateTime.now()…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
