蓝桥杯2023年第十四届省赛真题-平方差--题解
蓝桥杯2023年第十四届省赛真题-平方差
时间限制: 3s 内存限制: 320MB 提交: 2379 解决: 469
题目描述
给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 x = y2 − z2。
输入格式
输入一行包含两个整数 L, R,用一个空格分隔。
输出格式
输出一行包含一个整数满足题目给定条件的 x 的数量。
样例输入
复制
1 5
样例输出
复制
4
提示
1 = 1^2 − 0^2 ;
3 = 2^2 − 1^2 ;
4 = 2^2 − 0^2 ;
5 = 3^2 − 2^2 。
对于 40% 的评测用例,LR ≤ 5000 ;
对于所有评测用例,1 ≤ L ≤ R ≤ 10^9 。
【思路解析 】
在暴力尝试中总结答案的规律
【代码实现】
import java.util.Scanner;/*** @ProjectName: study3* @FileName: Ex1* @author:HWJ* @Data: 2023/9/16 22:27*/
public class Ex1 {public static void main(String[] args) {Scanner input = new Scanner(System.in);int L = input.nextInt();int R = input.nextInt();//System.out.println(getNums2(L, R));System.out.println(getNums3(L, R));}public static int getNums1(int L, int R){// 这个方法可行,但是时间复杂度为O(N^2),不满足题目要求int s = (R + 1) / 2;int e = (int) Math.sqrt(L) + 1;int ans = 0;boolean[] have = new boolean[R - L + 1];for (int i = s; i >= e; i--) {for (int j = i - 1; j >= 0; j--) {int a = (i + j) * (i - j);if (a >= L && a <= R && !have[a - L]) {ans++;have[a - L] = true;} else if (a > R) {break;}}}return ans;}public static int getNums2(int L, int R){// 通过观察所有可行的x发现 x要么为奇数要么为4的倍数int ans = 0;for (int i = L; i <= R; i++) {if (i % 4 == 0 || i % 2 != 0){ans++;}}return ans;}public static int getNums3(int L, int R){// 通过观察所有可行的x发现 x要么为奇数要么为4的倍数// 得到这个规律后,可以统计这样的数目应当为 F(R) = R / 4 + (R + 1) / 2;假设 L == 1// 所以实际数目应该为F(R) - F(L - 1)return (R / 4 + (R + 1) / 2) - ((L - 1) / 4 + (L) / 2);}
}
相关文章:

蓝桥杯2023年第十四届省赛真题-平方差--题解
蓝桥杯2023年第十四届省赛真题-平方差 时间限制: 3s 内存限制: 320MB 提交: 2379 解决: 469 题目描述 给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 x y2 − z2。 输入格式 输入一行包含两个整数 L, R,用一个空格分隔。 输出格…...

iText实战--根据绝对位置添加内容
3.1 direct content 概念简介 pdf内容的4个层级 层级1:在text和graphics底下,PdfWriter.getDirectContentUnder() 层级2:graphics层,Chunk, Images背景,PdfPCell的边界等 层级3:text层,Chun…...
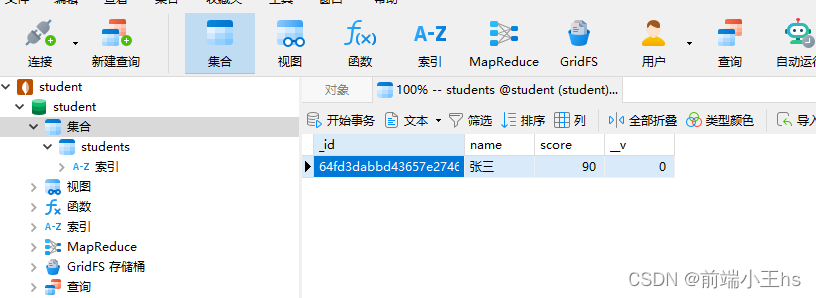
使用navicat for mongodb连接mongodb
使用navicat for mongodb连接mongodb 安装navicat for mongodb连接mongodb 安装navicat for mongodb 上文mongodb7.0安装全过程详解我们说过,在安装的时候并没有勾选install mongodb compass 我们使用navicat去进行可视化的数据库管理 navicat for mongodb下载地址…...
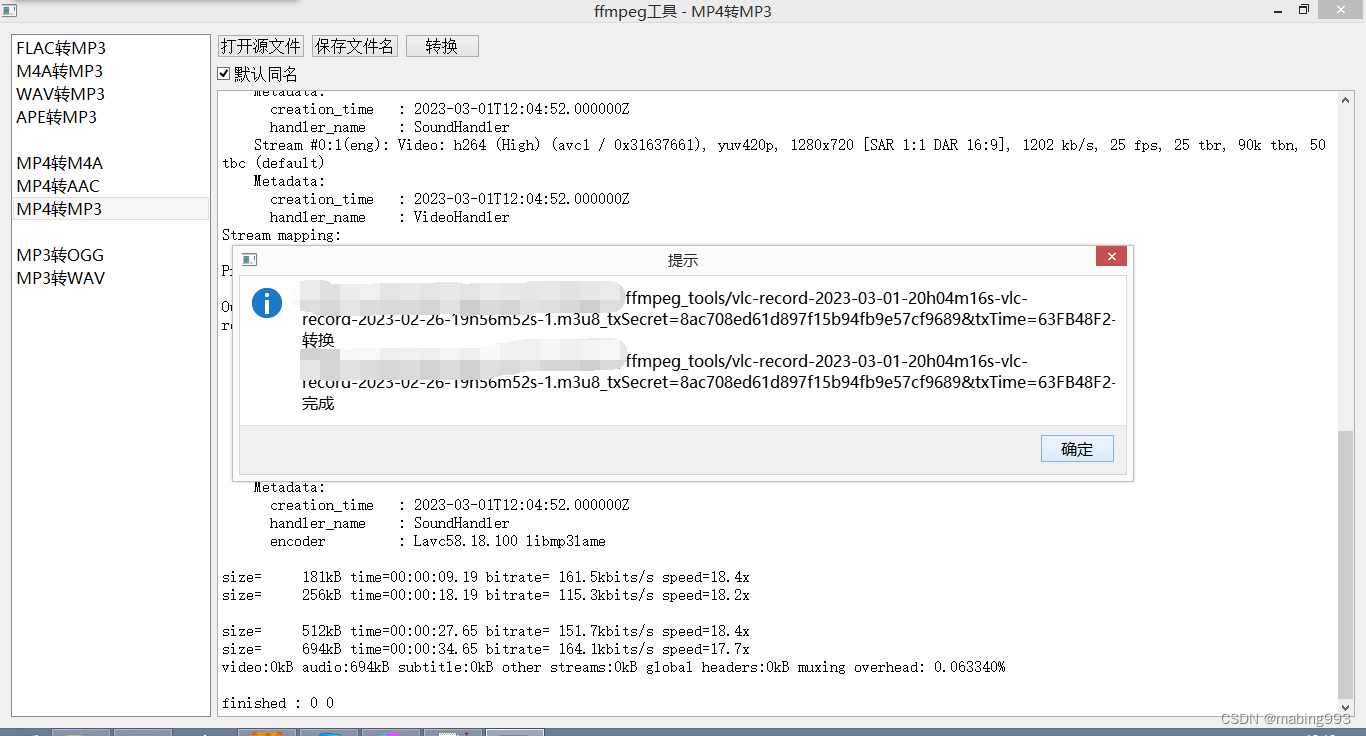
Qt ffmpeg音视频转换工具
Qt ffmpeg音视频转换工具,QProcess方式调用ffmpeg,对音视频文件进行格式转换,支持常见的音视频格式,主要在于QProcess的输出处理以及转换的文件名和后缀的处理,可以进一步加上音视频剪切合并和音视频文件属性查询修改的…...

机器学习笔记 - 视频分析和人类活动识别技术路线简述
一、理解人类活动识别 首先了解什么是人类活动识别,简而言之,是对某人正在执行的活动/动作进行分类或预测的任务称为活动识别。 我们可能会有一个问题:这与普通的分类任务有什么不同?这里的问题是,在人类活动识别中,您实际上需要一系列数据点来预测正确执行的动作。 看看…...
)
Redis从入门到精通(三:常用指令)
前边我们介绍了redis存储的四种基本数据类型,并纵向介绍了这四种数据类型的各种指令操作,现在我们这个章节从横向来总结一下关于key的常用指令和数据库常用指令 key常用指令 删除指定key del key 获取key是否存在 exists key 获取key的类型 type …...

代码随想录day39 || 动态规划 || 不同路径
62.不同路径 ● 力扣题目链接 ● 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 ● 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 ● 问总共有…...

电商平台API接口采集电商平台淘宝天猫京东拼多多数据获取产品详情信息,销量,价格,sku案例
淘宝SKU详情接口是指,获取指定商品的SKU(Stock Keeping Unit,即库存量单位)的详细信息。SKU是指提供不同的商品参数组合的一个机制,通过不同的SKU来标识商品的不同组合形式,如颜色、尺寸等。SKU详情接口可以…...

The ‘<‘ operator is reserved for future use. 错误解决
The < operator is reserved for future use. 错误解决 在 PowerShell 终端执行 python learnstock.py < ldata.txt 发生错误, The < operator is reserved for future use.解决方法, cmd /c python learnstock.py < ldata.txt完结&#x…...
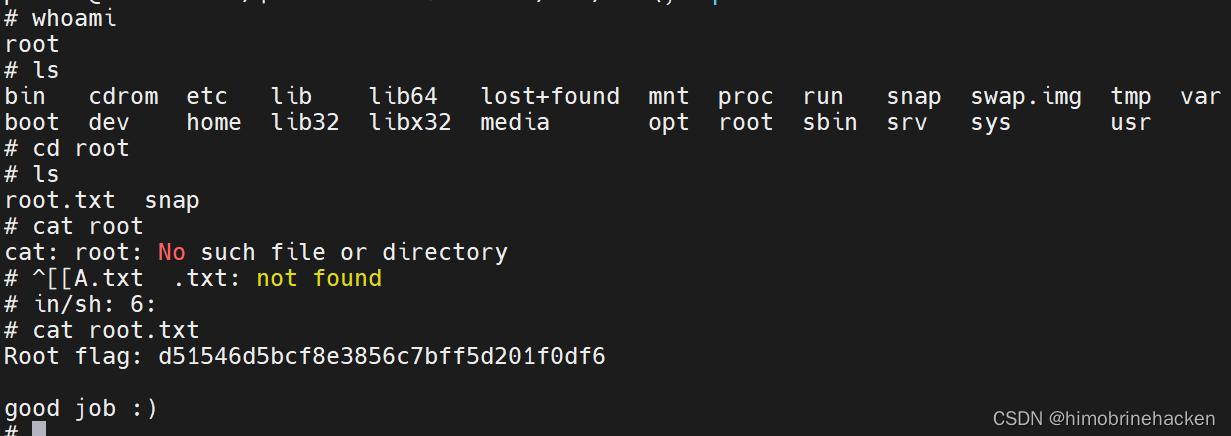
vulnhub靶机Thoth-Tech
下载地址:https://download.vulnhub.com/thothtech/Thoth-Tech.ova 主机发现 arp-scan -l 目标:192.168.21.148 端口扫描 nmap --min-rate 10000 -p- 192.168.21.148 服务扫描 nmap -sV -sT -O -p21,22,80 192.168.21.148 漏洞扫描 nmap --scriptvu…...
不可思议,无密码登录所有网站!
hello,我是小索奇 居然可以免密码登录你的网站?听起来是不是很恐怖 确实如此,Cookie可以用于保持用户在网站上的登录状态,从而实现 免密码登录,学会了不要做坏事哈 这里仅做免密码登录的实操,就不介绍Cooki…...

深度学习编译器关键组件
1 高层中间代码 为了克服传统编译器中采用的IR限制DL模型中复杂计算的表达的局限性,现有的DL编译器利用高层IR(称为图IR)进行高效的代码优化设计。 1.1 图表示 基于DAG的IR:基于DAG的IR是编译器构建计算图的最传统方法之一&…...
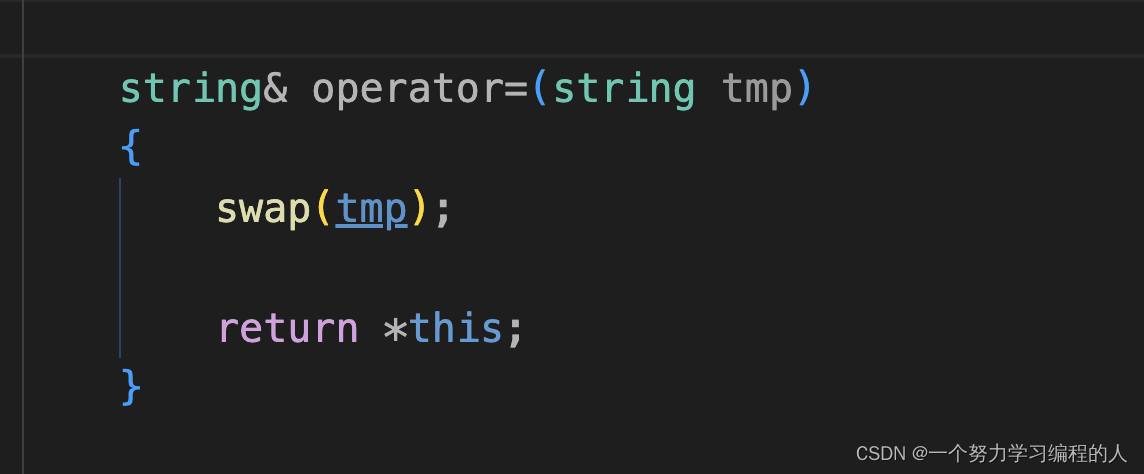
【C++】string类模拟实现下篇(附完整源码)
目录 1. resize2. 流插入<<和流提取>>重载2.1 流插入<<重载2.2 流提取 << 3. 常见关系运算符重载4. 赋值重载4.1浅拷贝的默认赋值重载4.2 深拷贝赋值重载实现4.3 赋值重载现代写法 5. 写时拷贝(了解)6.源码6.1 string.h6.2 test.cpp 1. res…...

Android高级开发-APK极致优化
九道工序 1. SVG(Scalable Vector Graphics)可缩放矢量图 使用矢量图代替位图可以减小 APK 的尺寸,因为可以针对不同屏幕密度调整同一文件的大小,而不会降低图像质量。 矢量图首次加载时可能消耗更多的 CPU 资源。之后,二者的内存使用率和…...
Rocketmq--消息驱动
1 MQ简介 1.1 什么是MQ MQ(Message Queue)是一种跨进程的通信机制,用于传递消息。通俗点说,就是一个先进先出的数据结构。 1.2 MQ的应用场景 1.2.1 异步解耦 最常见的一个场景是用户注册后,需要发送注册邮件和短信通…...

华为云云耀云服务器L实例评测|centos系统搭建git私服
搭建git私服 前言一、华为云云耀云服务器L实例租用二、华为云云耀云服务器L实例安装git三、华为云云耀云服务器L实例git配置1.创建文件用于存放公钥2.设置文件权限3.配置本地公钥 四、华为云云耀云服务器L实例部署git仓库四、git仓库到本地总结 前言 之前一直想搭建一个属于自…...

苹果CMS主题 MXonePro二开优化修复开源版影视网站源码
MXPro模板主题(又名:mxonepro)是一款基于苹果cms程序的一款全新的简洁好看UI的影视站模板类似于西瓜视频,不过同对比MxoneV10魔改模板来说功能没有那么多,也没有那么大气,但是比较且可视化功能较多简洁且有周更记录样式等多功能后台设置&…...

【新版】系统架构设计师 - 软件架构设计<轻量级架构>
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 软件架构设计<轻量级架构>考点摘要轻量级架构表示层业务逻辑层持久层数据库 SSH与SSMORMHibernate与Mybatis 架构 - 软件架构设计<轻量级架构> 考点…...
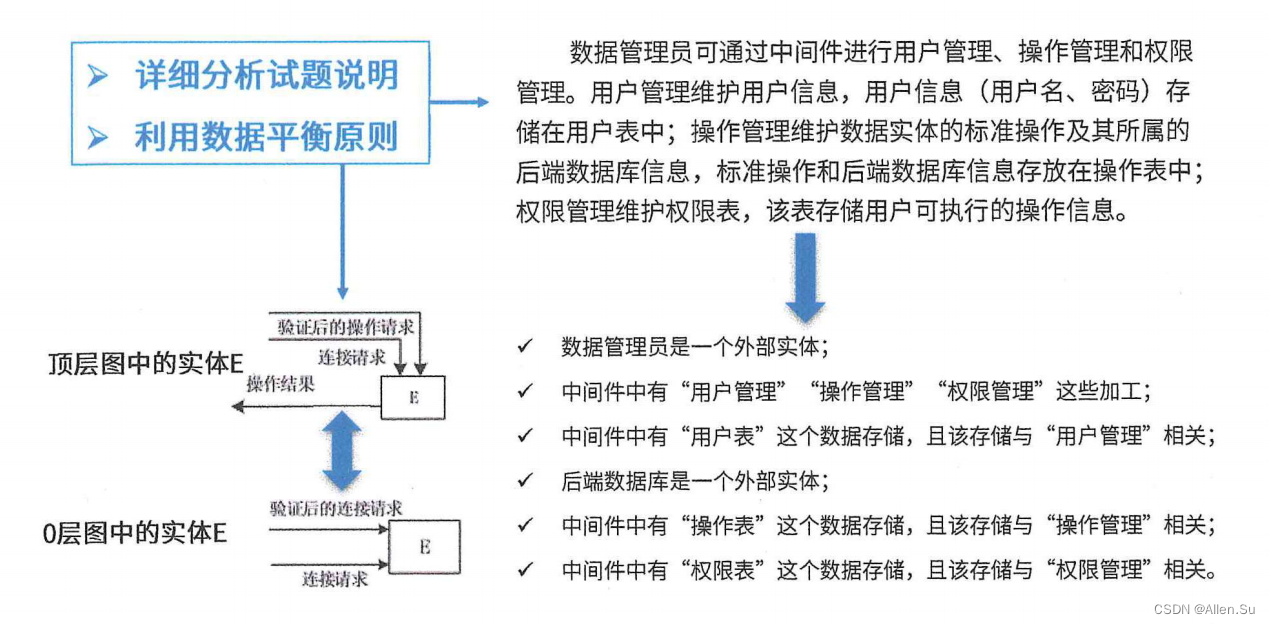
系统架构设计专业技能 ·结构化需求分析 - 数据流图
现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everything is for the future of dream weaving wings, let the dream fly in reality. 点击进入系列文章目录 系统架构设计高级技能 结构化需求分析 - 数据流图 一、数据流图的基本概念二、需…...

linux内核分析:线程和进程创建,内存管理
lec18-19:进程与线程创建 lec20-21虚拟内存管理 内核代码,全局变量这些只有一份,但是内核栈有多份,这可能就是linux线程模型1对1模式的由来。通过栈来做的 x86 CPU支持分段和分页(平坦内存模式)两种 分段,选择子那里就有特权标记了...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
