差分方程模型:国民总收入(GDP)的乘数-加速数模型
【背景知识-凯恩斯经济增长模型】
凯恩斯(John M.Keynes)建立了著名的国民经济增长模型。令Y表示国民总收入,C表示总消费,E为总支出,I表示投资,G为政府的投入(如基建等)。那么有
 【6.1】
【6.1】
其中,c0表示最低消费,它由储蓄率等决定;c(0≤c≤1)称为边际消费,反映了消费随着收入增加而增加的系数。
在[6.1]里,令Y=E,即有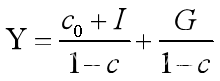 【6.2】
【6.2】
由【6.2】看出,I,G越大,Y越大;c越大,Y越大。即扩大消费、增加投资和国家投入可以促进国民总收入的增加。其中 称为乘数。
称为乘数。
【问题提出】
扩大消费促进投资,从而增加国民收入。诺贝尔经济学奖1970年获得者萨缪尔森(P.A.Samuelson)建立了一个十分简单的乘数-加速数模型,并可以化为一个二阶差分方程,通过求解此方程就可以解释经济增长中的一些重要现象。
【符号说明】
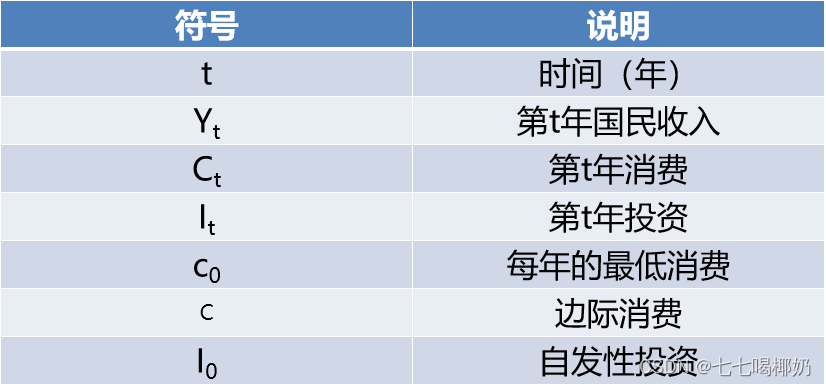
【模型构建】
第t年的国民总收入等于当年的总消费与总投资之和,即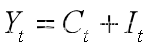
第t年的总消费等于基本消费c0与上一年的总收入与边际消费c之和 ![]()
第t年的总投资等于自发性投资与诱发性投资之和,即 ![]()
其中,β(0≤β≤1)刻画消费增长对投资的刺激作用。
总结上面的分析结果,就得到如下数学模型
 【6.3】
【6.3】
三个方程迭代后,整理出 【6.4】
【6.4】
这是一个关于国民收入的二阶常系数线性非齐次差分方程。其对应的齐次方程所对应的特征方程为

关于根的判别式为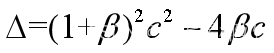
特征方程的两个根为
又由韦达定理, 所以有
所以有![]()
即特征根只有两种情况:![]()
令 代入【6.4】解得
代入【6.4】解得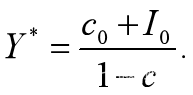 此平衡点稳定的充分必要条件是特征根都位于单位圆内,即
此平衡点稳定的充分必要条件是特征根都位于单位圆内,即![]() 【6.5】
【6.5】
即国民收入Y的用于消费的比例c和消费增量用于投资的比例β满足【6.5】即可。
相关文章:
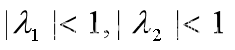
差分方程模型:国民总收入(GDP)的乘数-加速数模型
【背景知识-凯恩斯经济增长模型】 凯恩斯(John M.Keynes)建立了著名的国民经济增长模型。令Y表示国民总收入,C表示总消费,E为总支出,I表示投资,G为政府的投入(如基建等)。那么有 【6.1】 其中࿰…...

【C语言】指针和数组笔试题解析(1)
指针是C语言的灵魂,他的玩法多种多样,这篇文章带来指针的笔试题详解,可以帮助我们更好的理解与巩固指针的知识 目录 预备知识:题目:一维数组:二维数组: 题目比较多,但切记戒骄戒躁&a…...

Vue中组件的三种注册方式
组件的注册 1.全局注册: 在全局注册中,你需要确保在 Vue 根实例之前导入并注册组件。通常,你会在入口文件(例如 main.js)中执行这些操作。 // main.jsimport Vue from vue; import App from ./App.vue;// 导入全局组…...
docker 和k8s 入门
docker 和k8s 入门 本文是云原生的学习记录,可以参考以下文档 k8s https://www.yuque.com/leifengyang/oncloud 相关视频教程可参考如下 https://www.bilibili.com/video/BV13Q4y1C7hS?p2&vd_source0882f549dac54045384d4a921596e234 相对于公有云&#x…...

基于Yolov8的交通标志牌(TT100K)识别检测系统
1.Yolov8介绍 Ultralytics YOLOv8是Ultralytics公司开发的YOLO目标检测和图像分割模型的最新版本。YOLOv8是一种尖端的、最先进的(SOTA)模型,它建立在先前YOLO成功基础上,并引入了新功能和改进,以进一步提升性能和灵活…...

使用Python编写一个多线程的12306抢票程序
国庆长假即将到来,大家纷纷计划着自己的旅行行程。然而,对于很多人来说,抢购火车票人们成了一个令人头疼的问题。12306网站的服务器经常因为流量高而崩溃,导致抢票变得越来越严重异常困难。 首先,让我们来了解一下1230…...

DT Paint Effects工具(三)
管 分支 使用细枝 叶 力 使用湍流 流动画 渲染全局参数 建造盆栽植物...
SpringBoot整合Mybatis
目录 (1)引入依赖 (2)编写Mapper接口 (3)编写Mapper映射文件 (4)编写yml配置文件 (5)编写测试类 (1)引入依赖 <dependency>…...

Java后端使用POST请求向mysql中插入Json数据的问题
1.后端请求正常 但数据表中value没有值 原因 json数据属性不符合spring解析格式,json属性名称的大写字母不符合spring要求 以下为为错误示范 1 Test 以大写字母开头, 2 tTest 小写字母开头,但是第二个字母是大写解决方案 实体类属性加上Jso…...

豆瓣图书评分数据的可视化分析
导语 豆瓣是一个提供图书、电影、音乐等文化产品的社区平台,用户可以在上面发表自己的评价和评论,形成一个丰富的文化数据库。本文将介绍如何使用爬虫技术获取豆瓣图书的评分数据,并进行可视化分析,探索不同类型、不同年代、不同…...
SpringBoot整合Easy-ES操作演示文档
文章目录 SpringBoot整合Easy-ES操作演示文档1 概述及特性1.1 官网1.2 主要特性 2 整合配置2.1 导入POM2.2 Yaml配置2.3 EsMapperScan 注解扫描2.4 配置Entity2.5 配置Mapper 3 基础操作3.1 批量保存3.2 数据更新3.3 数据删除3.4 组合查询3.5 高亮查询3.6 统计查询 4 整合异常4…...
IDEA控制台取消悬浮全局配置SpringBoot配置https
IDEA控制台取消悬浮 idea 全局配置 SpringBoot(Tomcat) 配置https,同时支持http 利用JDK生成证书 keytool -genkey -alias httpsserver -keyalg RSA -keysize 2048 -keystore server.p12 -validity 3650配置类 Configuration public class TomcatConfig {Value(&quo…...

MySQL8--my.cnf配置文件的设置
原文网址:MySQL8--my.cfg配置文件的设置_IT利刃出鞘的博客-CSDN博客 简介 本文介绍MySQL8的my.cnf的配置。 典型配置 [client] default-character-setutf8mb4[mysql] default-character-setutf8mb4[mysqld] #服务端口号 默认3306 port3306datadir /work/docker…...

Qt基于paintEvent自定义CharView
Qt基于paintEvent自定义CharView 鼠标拖动,缩放,区域缩放, 针对x轴,直接上代码 charview.h #ifndef CHARVIEW_H #define CHARVIEW_H#include <QWidget> #include <QPainter> #include <QPaintEvent> #inclu…...
Mac FoneLab for Mac:轻松恢复iOS数据,专业工具助力生活
如果你曾经不小心删除了重要的iOS数据,或者因为各种原因丢失了这些数据,那么你一定知道这种痛苦。现在,有一个名为Mac FoneLab的Mac应用程序,它专门设计用于恢复iOS数据,这可能是你的救星。 Mac FoneLab for Mac是一种…...

代码随想录二刷day30
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、力扣332. 重新安排行程二、力扣51. N 皇后三、力扣37. 解数独 一、力扣332. 重新安排行程 class Solution {private LinkedList<String> res;private Li…...
工业检测 ocr
采用OpenCV和深度学习的钢印识别_菲斯奇的博客-CSDN博客采用OpenCV和深度学习的钢印识别[这个帖子标题党了很久,大概9月初立贴,本来以为比较好做,后来有事情耽搁了,直到现在才有了一些拿得出手的东西。肯定不会太监的。好…...

LVS负载均衡群集
这里写目录标题 LVS负载均衡群集一.集群cluster与分布式1.特点:2.类型1)负载均衡群集 LB2)高可用群集 HA3)高性能运输群集 HPC 3.分布式1)特点 二.LVS1.lvs的工作原理2.lvs的三种工作模式1)NAT 地址转换2&a…...

安卓截屏;前台服务
private var mediaProjectionManager: MediaProjectionManager? nullval REQUEST_MEDIA_PROJECTION 10001private var isstartservice true//启动MediaService服务fun startMediaService() {if (isstartservice) {startService(Intent(this, MediaService::class.java))iss…...
C++ PrimerPlus 复习 第八章 函数探幽
第一章 命令编译链接文件 make文件 第二章 进入c 第三章 处理数据 第四章 复合类型 (上) 第四章 复合类型 (下) 第五章 循环和关系表达式 第六章 分支语句和逻辑运算符 第七章 函数——C的编程模块(上ÿ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
