235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
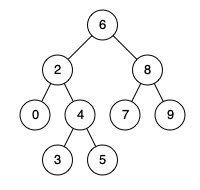
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点2和节点8的最近公共祖先是6。示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点2和节点4的最近公共祖先是2, 因为根据定义最近公共祖先节点可以为节点本身。说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==NULL)return root;if(root->val<q->val&&root->val<p->val)return lowestCommonAncestor(root->right,p,q);if(root->val>q->val&&root->val>p->val)return lowestCommonAncestor(root->left,p,q);else return root;}
};相关文章:
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己…...
DETR:End-to-End Object Detection with Transformers
代码:https://github.com/HuKai97/detr-annotations 论文:https://arxiv.org/pdf/2005.12872.pdf 参考视频:DETR 论文精读【论文精读】_哔哩哔哩_bilibili 团队:Meta AI 摘要 DETR 做目标检测任务既不需要proposal࿰…...
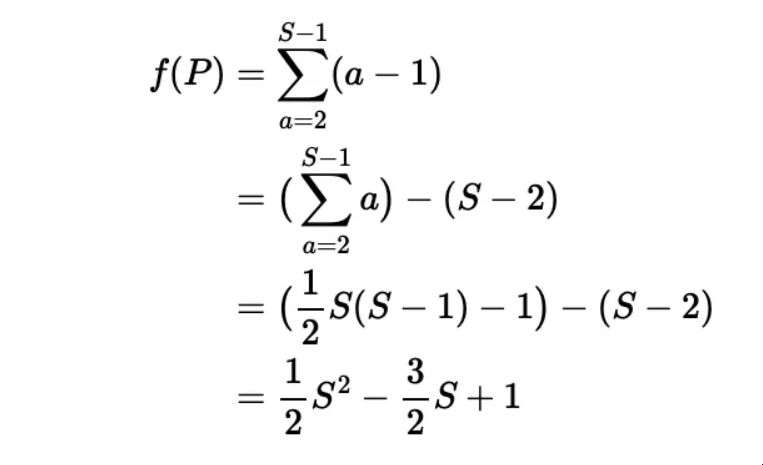
如何从第一性原则的原理分解数学问题
如何从第一性原则的原理分解数学问题 摘要:牛津大学入学考试题目展示了所有优秀数学家都使用的系统的第一原则推理,而GPT4仍然在这方面有困难 作者:Keith McNulty 我们中的许多人都熟悉直角三角形的边的规则。根据毕达哥拉斯定理,…...

实现strstr函数
一个字符串有没有在另一个字符串出现过 char* my_strstr(char* arr1, char* arr2) {char* cp;char* a1;char* a2;cp arr1;while (*cp){a1 cp;a2 arr2;while (*a1 *a2){a1;a2;}if (*a2 \0){return cp;}cp;}return NULL; } int main() {char arr1[] "abbbcdefgi"…...

C语言练习题解析(2)
💓博客主页:江池俊的博客⏩收录专栏:C语言刷题专栏👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
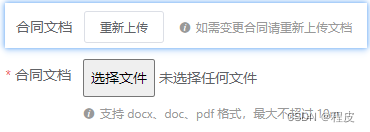
Element UI 表单验证规则动态失效问题
Element 版本:v2.15.3 问题背景 如下代码所示:有一个上传文件的 input 组件,在更新的时候,如果不上传文件表示不更新,如果要更新则点击 「重新上传」按钮将上传组件显示出来 <el-form ref"form" :mode…...
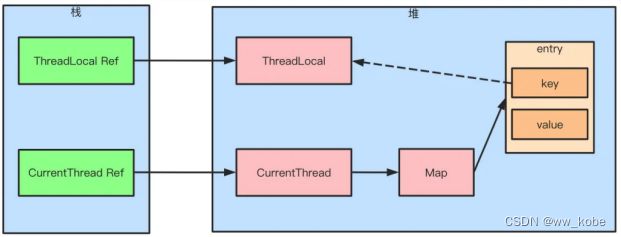
多线程并发篇
目录 1、线程生命周期 2、线程创建方式 3、Callable 与 Future 4、如何停止一个正在运行的线程 5、notify() 和 notifyAll() 的区别 6、sleep() 和 wait() 的区别 7、start() 和 run() 的区别 8、interrupted 和 isInterruptedd 的区别 9、CyclicBarrier 和 Count…...

pycharm-2023.1 closing project window stuck
pycharm-2023.1 closing project window stuck 问题描述 pycharm 切换项目/重启,一直卡在 closing project 原因分析 PyCharm 2023.1 issue - closing project window stuck (PyPIPackageUtil.lambda$parsePyPIListFromWeb) 解决方案 升级 pycharm 到 2023.3py…...

tkinter编写的打开csdn程序
目录 鬼畜tkinter简介程序代码解析现成总结鬼畜 看看你每次打开CSDN: 1.开机 2.打开浏览器 3.打开CSDN 4.等待 5.完成 我: 1.开机 2.点击%%%按钮 3.等待 4.完成 简单了不知道多少倍 上面的纯属鬼畜,下面正文!!! tkinter tkinter是一个用于创建图形用户界面(GUI)的Py…...

Vue3.2组件如何封装,以弹窗组件的封装为例
以前一直想,每次封装一个弹窗组件的时候,一直特别复杂,父传子,子传父,各种来回绕,来回修改。 一直想如何才能更加简化,但是一直没时间,今天终于抽时间出来封装了一下 本次封装简化…...
每天10个小知识点)
Vue知识系列(5)每天10个小知识点
目录 系列文章目录Vue知识系列(1)每天10个小知识点Vue知识系列(2)每天10个小知识点Vue知识系列(3)每天10个小知识点Vue知识系列(4)每天10个小知识点 知识点41.vue常用基本指令有哪些…...
)
Java基础题08——数组(查找下标所对应的值)
给定一个整数数组,输入一个值 n ,输出 n *在数组中的下标 **(*如果不存在输出 -1 ) 如:int[] arr {3, 2, 1, 4, 5}; 1 输入: 3 输出: 0 2. 输入: 6 输出: -1 int[] arr new int[]{3, 2, 1, 4,…...

LinkedList 源码分析
LinkedList 是一个基于双向链表实现的集合类。 LinkedList 插入和删除元素的时间复杂度 头部插入/删除:只需要修改头结点的指针即可完成插入/删除操作,因此时间复杂度为 O(1)。尾部插入/删除:只需要修改尾结点的指针即可完成插入/删除操作…...
)
跑步锻炼(蓝桥杯)
跑步锻练 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝每天都锻炼身体。 正常情况下,小蓝每天跑 1 千米。如果某天是周一或者月初(1 日),为了激励自己&#x…...

【SLAM】视觉SLAM简介
【SLAM】视觉SLAM简介 task04 主要了解了SLAM的主流框架,清楚VSALM中间接法与直接法的主要区别在什么地方,其各自的优势是什么,了解前端与后端的关系是什么 1.什么是SLAM 2.VSALM中间接法与直接法的主要区别在什么地方,其各自的…...
Visual Studio2019报错
1- Visual Studio2019报错 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法 小伙伴们在更新到Visual Studio2019后编译项目时可能遇到过这个错误:“ 错误 MSB8036 找不到 Windows SDK 版本 10.0.19041.0的解决方法”,但是我们明明安装了该…...

ffplay源码解析-PacketQueue队列
包队列架构位置 对应结构体源码 MyAVPacketList typedef struct MyAVPacketList {AVPacket pkt; //解封装后的数据struct MyAVPacketList *next; //下一个节点int serial; //播放序列 } MyAVPacketList;PacketQueue typedef struct PacketQueue {MyAVPacketList …...

Flowable主要API介绍
1. ProcessEngine 负责与各个服务进行交互和管理流程的整个生命周期。 方法描述getName()close()startExecutors()启动所有流程引擎中的执行器。执行器用于处理流程实例的执行,在引擎启动时,执行器会自动运行并处理待办任务和定时任务。getRepositorySe…...

TensorFlow与pytorch特定版本虚拟环境的安装
TensorFlow与Python的版本对应,注意,一定要选择对应的版本,否则会让你非常痛苦,折腾很久搞不清楚原因。 建议使用国内镜像源安装 没有GPU后缀的就表示是CPU版本的,不加版本就是最新 pip install tensorflow -i https:…...

【SpringMVC】拦截器JSR303的使用
【SpringMVC】拦截器&JSR303的使用 1.1 什么是JSR3031.2 为什么使用JSR3031.3 常用注解1.4 Validated与Valid区别1.5 JSR快速入门1.5.2 配置校验规则# 1.5.3 入门案例二、拦截器2.1 什么是拦截器2.2 拦截器与过滤器2.3 应用场景2.4 拦截器快速入门2.5.拦截器链2.6登录案列权…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
