LeetCode 周赛上分之旅 #45 精妙的 O(lgn) 扫描算法与树上 DP 问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 45 篇文章,往期回顾请移步到文章末尾~
LeetCode 双周赛 113 概览
T1. 使数组成为递增数组的最少右移次数(Easy)
- 标签:模拟、暴力、线性遍历
T2. 删除数对后的最小数组长度(Medium)
- 标签:二分答案、双指针、找众数、
T3. 统计距离为 k 的点对(Medium)
- 标签:枚举、散列表
T4. 可以到达每一个节点的最少边反转次数(Hard)
- 标签:树上 DP

T1. 使数组成为递增数组的最少右移次数(Easy)
https://leetcode.cn/problems/minimum-right-shifts-to-sort-the-array/description/
题解一(暴力枚举)
简单模拟题。
由于题目数据量非常小,可以把数组复制一份拼接在尾部,再枚举从位置 i i i 开始长为 n n n 的连续循环子数组是否连续,是则返回 ( n − i ) % n (n - i)\%n (n−i)%n:
class Solution {fun minimumRightShifts(nums: MutableList<Int>): Int {val n = nums.sizenums.addAll(nums)for (i in 0 until n) {if ((i + 1 ..< i + n).all { nums[it] > nums[it - 1]}) return (n - i) % n}return -1}
}
class Solution:def minimumRightShifts(self, nums: List[int]) -> int:n = len(nums)nums += numsfor i in range(0, n):if all(nums[j] > nums[j - 1] for j in range(i + 1, i + n)):return (n - i) % nreturn -1
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2) 双重循环;
- 空间复杂度: O ( n ) O(n) O(n) 循环数组空间。
题解二(线性遍历)
更优的写法,我们找到第一个逆序位置,再检查该位置后续位置是否全部为升序,且满足 n u m s [ n − 1 ] < n u m s [ 0 ] nums[n - 1] < nums[0] nums[n−1]<nums[0]:
class Solution {fun minimumRightShifts(nums: List<Int>): Int {val n = nums.sizefor (i in 1 until n) { // 第一段if (nums[i] >= nums[i - 1]) continue// 第二段if (nums[n - 1] > nums[0]) return -1for (j in i until n - 1) { if (nums[j] > nums[j + 1]) return -1}return n - i}return 0}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) i i i 指针和 j j j 指针总计最多移动 n n n 次;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
T2. 删除数对后的最小数组长度(Medium)
https://leetcode.cn/problems/minimum-array-length-after-pair-removals/
题解一(二分答案)
问题存在单调性:
- 当操作次数 k k k 可以满足时,操作次数 k − 1 k - 1 k−1 一定能满足;
- 当操作次数 k k k 不可满足时,操作次数 k + 1 k + 1 k+1 一定不能满足。
那么,原问题相当于求解满足目标的最大操作次数。
现在需要考虑的问题是:如何验证操作次数 k k k 是否可以完成?
一些错误的思路:
- 尝试 1 - 贪心双指针: n u m s [ i ] nums[i] nums[i] 优先使用最小值, n u m s [ j ] nums[j] nums[j] 优先使用最大值,错误用例: [ 1236 ] [1 2 3 6] [1236];
- 尝试 2 - 贪心: n u m s [ i ] nums[i] nums[i] 优先使用最小值, n u m s [ j ] nums[j] nums[j] 使用大于 n u m s [ i ] nums[i] nums[i] 的最小值,错误用例: [ 1246 ] [1 2 4 6] [1246];
- 尝试 3 - 贪心: 从后往前遍历, n u m s [ i ] nums[i] nums[i] 优先使用较大值, n u m s [ j ] nums[j] nums[j] 使用大于 n u m s [ i ] nums[i] nums[i] 的最小值,错误用例: [ 2348 ] [2 3 4 8] [2348]。
开始转换思路:
能否将数组拆分为两部分,作为 nums[i] 的分为一组,作为 n u m s [ j ] nums[j] nums[j] 的分为一组。 例如,在用例 [ 12 ∣ 36 ] [1 2 | 3 6] [12∣36] 和 [ 12 ∣ 46 ] [1 2 | 4 6] [12∣46] 和 [ 23 ∣ 48 ] [2 3 | 4 8] [23∣48] 中,将数组的前部分作为 n u m s [ i ] nums[i] nums[i] 而后半部分作为 n u m s [ j ] nums[j] nums[j] 时,可以得到最优解,至此发现贪心规律。
设数组的长度为 n n n,最大匹配对数为 k k k:
- 结论 1: 使用数组的左半部分作为 n u m s [ i ] nums[i] nums[i] 且使用数组的右半部分作为 n u m s [ j ] nums[j] nums[j] 总能取到最优解。反之,如果使用右半部分的某个数 n u m s [ t ] nums[t] nums[t] 作为 n u m s [ i ] nums[i] nums[i],相当于占用了一个较大的数,不利于后续 n u m s [ i ] nums[i] nums[i] 寻找配对;
- 结论 2: 当固定 n u m s [ i ] nums[i] nums[i] 时, n u m s [ j ] nums[j] nums[j] 越小越好,否则会占用一个较大的位置,不利于后续 n u m s [ i ] nums[i] nums[i] 寻找配对。因此最优解一定是使用左半部分的最小值与右半部分的最小值配对。
总结:如果存在 k k k 对匹配,那么一定可以让最小的 k k k 个数和最大的 k k k 个数匹配。
基于以上分析,可以写出二分答案:
class Solution {fun minLengthAfterRemovals(nums: List<Int>): Int {val n = nums.sizevar left = 0var right = n / 2while (left < right) {val k = (left + right + 1) ushr 1if ((0 ..< k).all { nums[it] < nums[n - k + it] }) {left = k} else {right = k - 1}}return n - 2 * left}
}
复杂度分析:
- 时间复杂度: O ( n l g n ) O(nlgn) O(nlgn) 二分答案次数最大为 l g n lgn lgn 次,单次检验的时间复杂度是 O ( n ) O(n) O(n);
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
题解二(双指针)
基于题解一的分析,以及删除操作的上界 n / 2 n / 2 n/2,我们可以仅使用数组的后半部分与前半部分作比较,具体算法:
- i 指针指向索引 0 0 0
- j 指针指向索引 ( n + 1 ) / 2 (n + 1) / 2 (n+1)/2
- 向右枚举 j j j 指针,如果 i i i、 j j j 指针指向的位置能够匹配,则向右移动 i i i 指针;
- 最后 i i i 指针移动的次数就等于删除操作次数。
class Solution {fun minLengthAfterRemovals(nums: List<Int>): Int {val n = nums.sizevar i = 0for (j in (n + 1) / 2 until n) {if (nums[i] < nums[j]) i++}return n - 2 * i}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
题解三(众数)
由于题目的操作只要满足 n u m s [ i ] < n u m s [ j ] nums[i] < nums[j] nums[i]<nums[j],即两个数不相等即可,那么问题的解最终仅取决于数组中的众数的出现次数:
- 如果众数的出现次数比其他元素少,那么所有元素都能删除,问题的结果就看数组总长度是奇数还是偶数;
- 否则,剩下的元素就是众数: s − ( n − s ) s - (n - s) s−(n−s)
最后,由于数组是非递减的,因此可以在 O ( 1 ) O(1) O(1) 空间求出众数的出现次数:
class Solution {fun minLengthAfterRemovals(nums: List<Int>): Int {val n = nums.sizevar s = 1var cur = 1for (i in 1 until n) {if (nums[i] == nums[i - 1]) {s = max(s, ++ cur)} else {cur = 1}}if (s <= n - s) {return n % 2} else {return s - (n - s)}}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
题解四(找规律 + 二分查找)
继续挖掘数据规律:
s < = n − s s <= n - s s<=n−s 等价于众数的出现次数超过数组长度的一半,由于数组是有序的,那么一定有数组的中间位置就是众数,我们可以用二分查找找出众数在数组中出现位置的边界,从而计算出众数的出现次数。
由此,我们甚至不需要线性扫描都能计算出众数以及众数的出现次数,Nice!
当然,最后计算出来的出现次数有可能没有超过数组长度的一半。
class Solution {fun minLengthAfterRemovals(nums: List<Int>): Int {val n = nums.sizeval x = nums[n / 2]val s = lowerBound(nums, x + 1) - lowerBound(nums, x)return max(2 * s - n, n % 2)}fun lowerBound(nums: List<Int>, target: Int): Int {var left = 0var right = nums.size - 1while (left < right) {val mid = (left + right + 1) ushr 1if (nums[mid] >= target) {right = mid - 1} else {left = mid}}return if (nums[left] == target) left else left + 1}
}
复杂度分析:
- 时间复杂度: O ( l g n ) O(lgn) O(lgn) 单次二分查找的时间复杂度是 O ( l g n ) O(lgn) O(lgn);
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
相似题目:
- 2576. 求出最多标记下标
T3. 统计距离为 k 的点对(Medium)
https://leetcode.cn/problems/count-pairs-of-points-with-distance-k/
题解(散列表)
- 问题目标: 求 ( x 1 x o r x 2 ) + ( y 1 x o r y 2 ) = = k (x1 xor x2) + (y1 xor y2) == k (x1xorx2)+(y1xory2)==k 的方案数;
- 技巧: 对于存在多个变量的问题,可以考虑先固定其中一个变量;
容易想到两数之和的问题模板,唯一需要思考的问题是如何设计散列表的存取方式:
对于满足 ( x 1 x o r x 2 ) + ( y 1 x o r y 2 ) = = k (x1\ xor\ x2) + (y1\ xor\ y2) == k (x1 xor x2)+(y1 xor y2)==k 的方案,我们抽象为两部分 i + j = k i + j = k i+j=k,其中, i = ( x 1 x o r x 2 ) i = (x1\ xor\ x2) i=(x1 xor x2) 的取值范围为 [ 0 , k ] [0, k] [0,k],而 j = k − i j = k - i j=k−i,即总共有 k + 1 k + 1 k+1 种方案。本题的 k k k 数据范围很小,所以我们可以写出时间复杂度 O ( n k ) O(nk) O(nk) 的算法。
class Solution {fun countPairs(coordinates: List<List<Int>>, k: Int): Int {var ret = 0// <x, <y, cnt>>val map = HashMap<Int, HashMap<Int, Int>>()for ((x2, y2) in coordinates) {// 记录方案for (i in 0 .. k) {if (!map.containsKey(i xor x2)) continueret += map[i xor x2]!!.getOrDefault((k - i) xor y2, 0)}// 累计次数map.getOrPut(x2) { HashMap<Int, Int>() }[y2] = map[x2]!!.getOrDefault(y2, 0) + 1}return ret}
}
Python 计数器支持复合数据类型的建,可以写出非常简洁的代码:
class Solution:def countPairs(self, coordinates: List[List[int]], k: int) -> int:c = Counter()ret = 0for x2, y2 in coordinates:# 记录方案for i in range(k + 1):ret += c[(i ^ x2, (k - i) ^ y2)]# 累计次数c[(x2, y2)] += 1return ret
复杂度分析:
- 时间复杂度: O ( n ⋅ k ) O(n·k) O(n⋅k) 线性枚举,每个元素枚举 k k k 种方案;
- 空间复杂度: O ( n ) O(n) O(n) 散列表空间。
T4. 可以到达每一个节点的最少边反转次数(Hard)
https://leetcode.cn/problems/minimum-edge-reversals-so-every-node-is-reachable/
问题分析
初步分析:
- 问题目标: 求出以每个节点为根节点时,从根节点到其他节点的反转操作次数,此题属于换根 DP 问题
思考实现:
- 暴力: 以节点 i i i 为根节点走一次 BFS/DFS,就可以在 O ( n ) O(n) O(n) 时间内求出每个节点的解,整体的时间复杂度是 O ( n 2 ) O(n^2) O(n2)
思考优化:
- 重叠子问题: 相邻边连接的节点间存在重叠子问题,当我们从根节点 u u u 移动到其子节点 v v v 时,我们可以利用已有信息在 O ( 1 ) O(1) O(1) 时间算出 v v v 为根节点时的解。
具体实现:
- 1、随机选择一个点为根节点 u u u,在一次 DFS 中根节点 u u u 的反转操作次数:
- 2、 u → v u → v u→v 的状态转移:
- 如果 u → v u → v u→v 是正向边,则反转次数 + 1 + 1 +1;
- 如果 u → v u → v u→v 是反向边,则反转次数 − 1 - 1 −1(从 v v v 到 u u u 不用反转);
- 3、由于题目是有向图,我们可以转换为无向图,再利用标记位 1 1 1 和 − 1 -1 −1 表示边的方向, 1 1 1 为正向边, − 1 -1 −1 为反向边。
题解(换根 DP)
class Solution {fun minEdgeReversals(n: Int, edges: Array<IntArray>): IntArray {val dp = IntArray(n)val graph = Array(n) { LinkedList<IntArray>() }// 建图for ((from, to) in edges) {graph[from].add(intArrayOf(to, 1))graph[to].add(intArrayOf(from, -1))}// 以 0 为根节点fun dfs(i: Int, fa: Int) {for ((to, gain) in graph[i]) {if (to == fa) continueif (gain == -1) dp[0] ++dfs(to, i)}}fun dp(i: Int, fa: Int) {for ((to, gain) in graph[i]) {if (to == fa) continue// 状态转移dp[to] = dp[i] + gaindp(to, i)}}dfs(0, -1)dp(0, -1)return dp}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) DFS 和换根 DP 都是 O ( n ) O(n) O(n);
- 空间复杂度: O ( n ) O(n) O(n) 递归栈空间与 DP 数组空间。
推荐阅读
LeetCode 上分之旅系列往期回顾:
- LeetCode 单周赛第 361 场 · 同余前缀和问题与经典倍增 LCA 算法
- LeetCode 单周赛第 360 场 · 当 LeetCode 考树上倍增,出题的趋势在变化吗
- LeetCode 双周赛第 112 场 · 计算机科学本质上是数学吗?
- LeetCode 双周赛第 111 场 · 按部就班地解决动态规划问题
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~

相关文章:

LeetCode 周赛上分之旅 #45 精妙的 O(lgn) 扫描算法与树上 DP 问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...

JavaScript-DOM实战案例
一、window定时器 1.window定时器方法 有时我们并不想立即执行一个函数,而是等待特定一段时间之后再执行,我们称之为“计划调用(scheduling a call)”。 目前有两种方式可以实现: setTimeout 允许我们将函数推迟到一…...
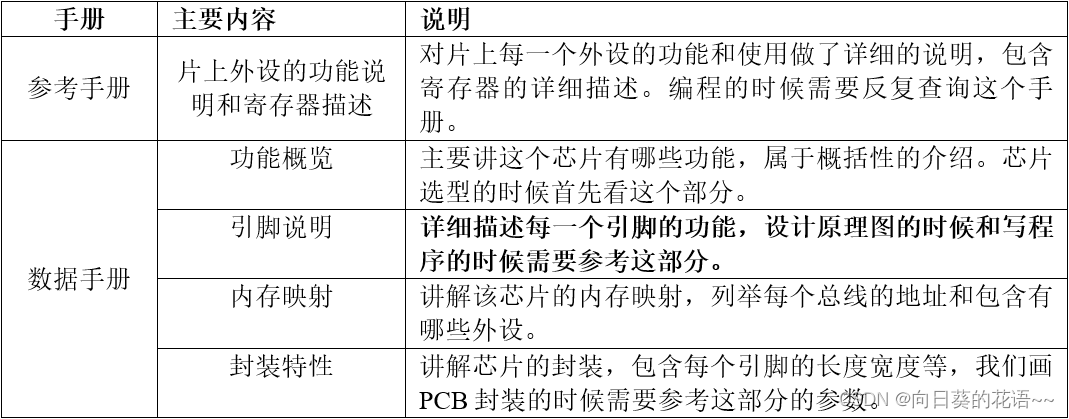
STM32 学习笔记1:STM32简介
1 概述 STM32,从字面上来理解,ST 是意法半导体,M 是 Microelectronics 的缩写,32 表示 32 位,合起来理解,STM32 就是 ST 公司开发的 32 位微控制器。是一款基于 ARM 公司推出的基于 ARMv7 架构的 32 位 Co…...

Hadoop-Hbase
1. Hbase安装 1.1 安装zookeeper、 hbase 解压至/opt/soft,并分别改名 配置环境变量并source生效 #ZK export ZOOKEEPER_HOME/opt/soft/zk345 export PATH$ZOOKEEPER_HOME/bin:$PATH #HBASE_HOME export HBASE_HOME/opt/soft/hbase235 export PATH$HBASE_HOME/b…...

关于不停机发布新版本程序的方式
“不停机发布新版本程序”,暂且这么称呼吧,其实就是所说的滚动发布、灰度发布、金丝雀发布和蓝绿发布。 之所以会总结性地提一下这几个概念,主要是本次出门游历,流浪到了乌兰察布市四王子旗,在这儿遇上了个有趣儿的家伙…...
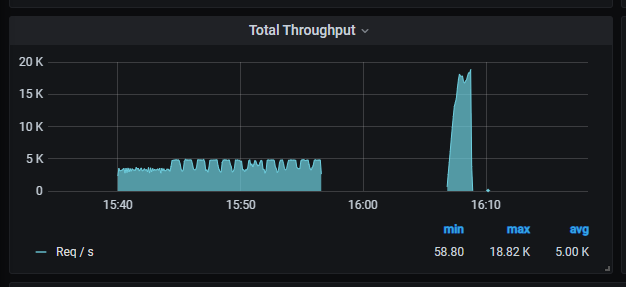
MeterSphere压测,出现HttpHostConnectException
现象:MeterSphere更换压力机后,压测出现出现HttpHostConnectException 解决方案: net.ipv4.tcp_tw_reuse默认是0或者2,更改为1 net.ipv4.tcp_tw_reuse,表示是否允许重新应用处于TIME-WAIT状态的socket用于新的TCP连…...

cherry-pick
要将dev分支的某次提交给master分支,可以使用以下命令: 1. 切换到dev分支:git checkout dev 2. 查看提交历史,找到要提交给master的某次提交的commit hash(假设为 <commit_hash>) 3. 切换到master…...
opencv形状目标检测
1.圆形检测 OpenCV图像处理中“找圆技术”的使用-图像处理-双翌视觉OpenCV图像处理中“找圆技术”的使用,图像处理,双翌视觉https://www.shuangyi-tech.com/news_224.htmlopencv 找圆心得,模板匹配比霍夫圆心好用 - 知乎1 相比较霍夫找直线算法, 霍夫找…...

k8s中无法获取到nginx-ingress的客户端真实ip地址x-forwarded-for
1.查看阿里云的nginx-ingress配置文档https://help.aliyun.com/document_detail/42205.html 容器K8s配置方案 如果您的服务部署在K8s上,K8s会将真实的客户端IP记录在X-Original-Forwarded-For字段中,并将WAF回源地址记录在X-Forwarded-For字段中。您需要…...
索引实践(2))
MySQL(4)索引实践(2)
一、分页优化 limit 1000 10, 其实不是只查询出10条记录,mysql底层会查询出1100条,然后舍去前1000条 所以,随着页的增多,查询效率会降低 1、可以使用取范围的方式比如id>1000 方式优化 2、使用关联查询优化…...

Kafka【命令行操作】
Kafka 命令行操作 Kafka 主要包括三大部分:生产者、主题分区节点、消费者。 1、Topic 命令行操作 也就是我们 kafka 下的脚本 kafka-topics.sh 的相关操作。 常用命令行操作 参数 描述 --bootstrap-server <String: server toconnect to> 连接的Kafka …...
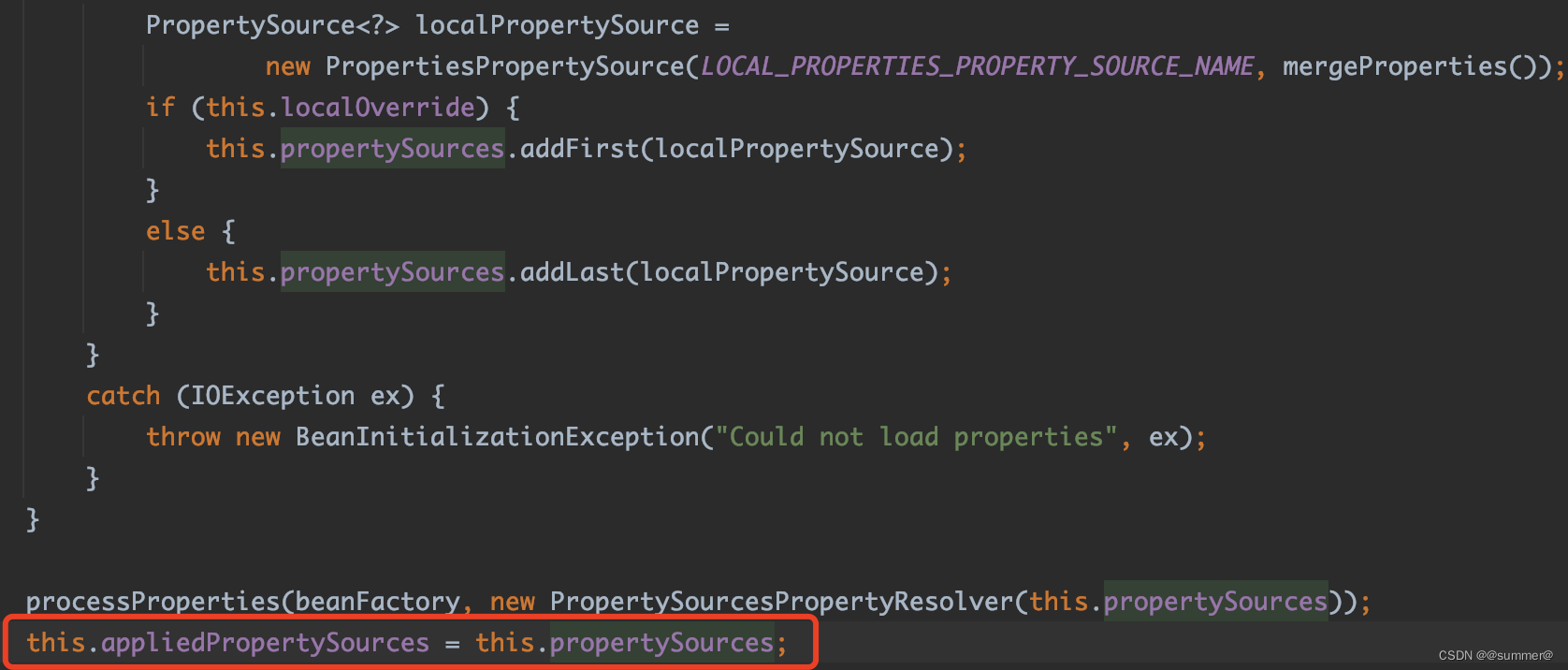
springboot配置注入增强(二)属性注入的原理
一 原理 1 配置的存储 springboot在启动的时候会后构建一个org.springframework.core.env.Environment类型的对象,这个对象就是用于存储配置,如图springboot会在启动的最开始创建一个Environment对象 这个webApplicationType的枚举是在new SpringAppli…...

Android 使用Camera1实现相机预览、拍照、录像
1. 前言 本文介绍如何从零开始,在Android中实现Camera1的接入,并在文末提供Camera1Manager工具类,可以用于快速接入Camera1。 Android Camera1 API虽然已经被Google废弃,但有些场景下不得不使用。 并且Camera1返回的帧数据是NV21…...
)
2024字节跳动校招面试真题汇总及其解答(四)
12.Java的类加载机制 Java的类加载机制是指将描述类的数据从Class文件加载到内存,并对数据进行校验、转换解析和初始化,最终形成可以被虚拟机直接使用的Java类型,这个过程被称作虚拟机的类加载机制。 类的加载过程分为以下五个阶段: 加载:将Class文件从磁盘读入内存,并…...
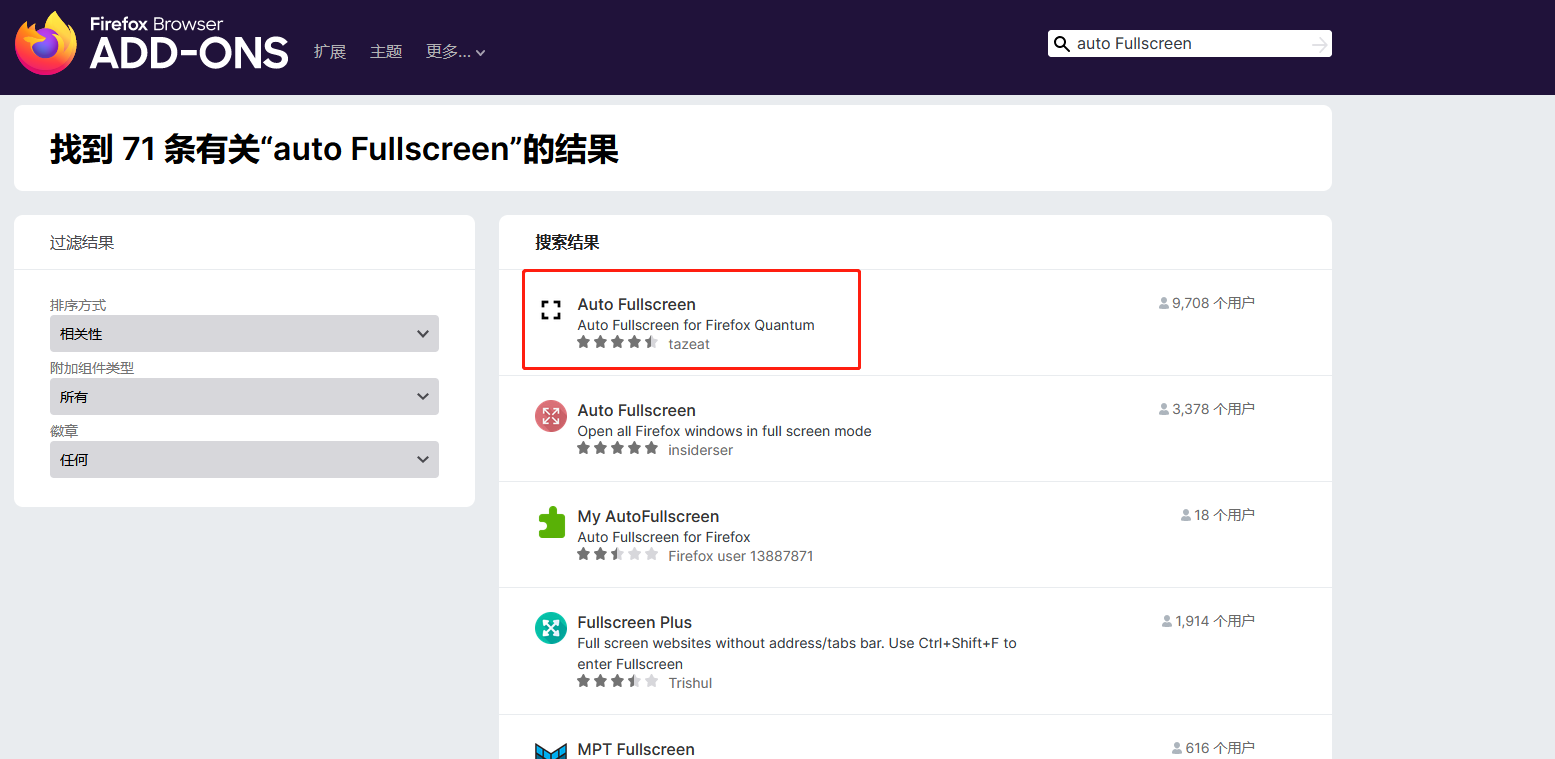
网页的快捷方式打开自动全屏--Chrome、Firefox 浏览器相关设置
Firefox 的全屏方式与 Chrome 不同,Chrome 自带全屏模式以及APP模式,通过简单的参数即可设置,而Firefox暂时么有这个功能,Firefox 的全屏功能可以通过全屏插件实现。 全屏模式下,按 F11 不会退出全屏,鼠标…...
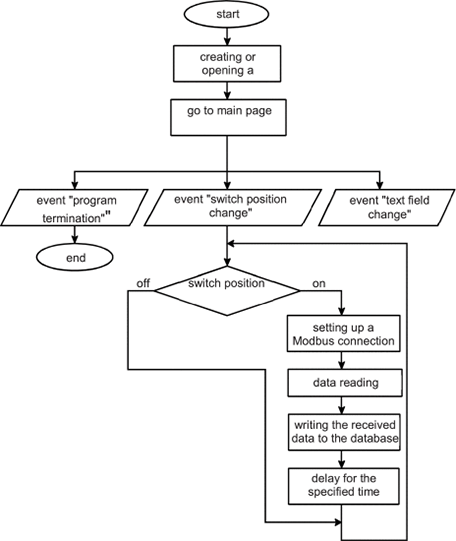
LabVIEW使用ModbusTCP协议构建分布式测量系统
LabVIEW使用ModbusTCP协议构建分布式测量系统 分布式测量系统主要用于监控远程物体。这种系统允许对系统用户获得的数据进行全面的数据收集、处理、存储和组织访问。它们可能包括许多不同类型的传感器。 在任何具有互联网接入的个人计算机上运行的软件都会发送来自传感器的测…...
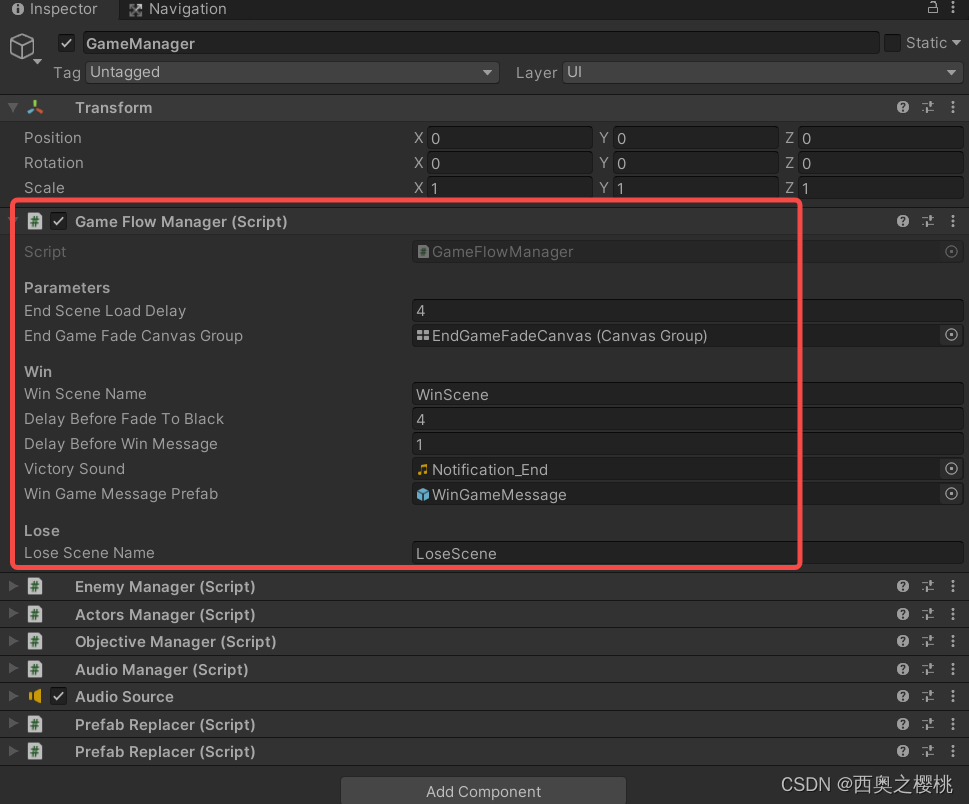
unity学习第1天
本身也具有一些unity知识,包括Eidtor界面使用、Shader效果实现、性能分析,但对C#、游戏逻辑不太清楚,这次想从开发者角度理解游戏,提高C#编程,从简单的unity游戏理解游戏逻辑,更好的为工作服务。 unity201…...

Spring Boot实现对文件进行压缩下载
在Web应用中,文件下载功能是一个常见的需求,特别是当你需要提供用户下载各种类型的文件时。本文将演示如何使用Spring Boot框架来实现一个简单而强大的文件下载功能。我们将创建一个RESTful API,通过该API,用户可以下载问价为ZIP压…...
Mac专用投屏工具AirServer 7 .27 for Mac中文免费激活版
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...
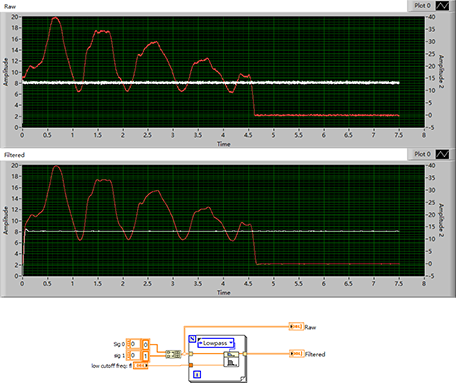
LabVIEW使用巴特沃兹低通滤波器过滤噪声
LabVIEW使用巴特沃兹低通滤波器过滤噪声 设备采集到的数据往往都有噪声,有时候这些数据要做判断使用,如果不处理往往会影响最终的结果。可以使用动态平滑,或者中值滤波等方法。这里介绍使用巴特沃斯低通滤波,也是非常方便的。 下…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
