程序员在线周刊(冒泡算法篇)
大家好,欢迎来到程序员在线周刊!本期我们将深入探讨一种经典的排序算法——冒泡算法,并附上具体的代码实现。
目录
- 简介
- 代码
- 原理
- 广告
- 广告1
- 广告2
- 广告3
简介
冒泡算法是一种简单但效率较低的排序算法,它的原理非常直观:通过相邻元素的比较和交换,将最大(或最小)的元素逐渐“冒泡”到数列的末尾。下面让我以第一人称的口吻给大家讲解一下。
首先,让我们来看一下冒泡算法的代码实现:
代码
def bubble_sort(arr):n = len(arr)for i in range(n - 1): # 外层循环控制比较轮数for j in range(n - i - 1): # 内层循环控制每轮的比较次数if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j] # 交换元素位置arr = [4, 2, 7, 1, 3]
bubble_sort(arr)
print("排序结果为:", arr)
原理
以上就是冒泡排序算法的代码实现。首先,我们定义一个函数bubble_sort,传入一个待排序的数组arr。然后,我们使用两层循环来比较相邻元素,如果前一个元素大于后一个元素,就进行交换。通过这样的操作,每一轮比较都可以将最大的元素“冒泡”到数列的末尾。最终,就能够获得一个有序的数组。
那么,冒泡排序的时间复杂度是多少呢?由于我们需要进行两层循环,外层循环执行 n - 1 次,内层循环执行 n - i - 1 次,所以总的比较次数是 ( n − 1 ) + ( n − 2 ) + . . . + 1 (n - 1) + (n - 2) + ... + 1 (n−1)+(n−2)+...+1,也就是 n × ( n − 1 ) ÷ 2 n \times (n - 1) \div 2 n×(n−1)÷2。因此,冒泡排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。在实际应用中,如果待排序的数组较大,冒泡排序可能会显得比较慢,但对于小型数据集来说,冒泡算法还是个不错的选择。
希望通过本期的介绍,大家对冒泡算法有了更深入的了解。如有任何疑问或意见,欢迎在评论区留言,我们下期再见!
广告
广告1
程序员在线周刊正在征集稿件
链接:http://t.csdn.cn/o5LYu
广告2
《Python与Unity专栏》开始啦!!!快去看看订阅吧!
链接:http://t.csdn.cn/nGiXC
广告3
广告位招租!想投广告的请关注再私信我!
相关文章:
)
程序员在线周刊(冒泡算法篇)
大家好,欢迎来到程序员在线周刊!本期我们将深入探讨一种经典的排序算法——冒泡算法,并附上具体的代码实现。 目录 简介代码原理广告广告1广告2广告3 简介 冒泡算法是一种简单但效率较低的排序算法,它的原理非常直观:…...

string
目录 六、STL简介 (一)什么是STL (二)STL的版本 (三)STL六大组件 七、string (一)标准库中的string 1、string类 2、string常用的接口 1)string类对象的常见构造 2)string类对象的容量操作 3)string类对象的访问及遍历操作 4)string类对象的修改操作 5)string类非成…...
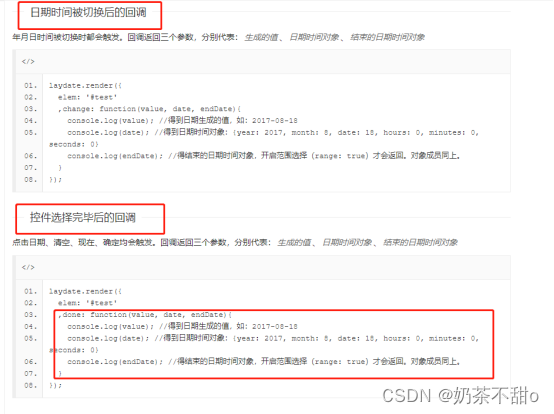
html的日期选择插件
1.效果 2.文档 https://layui.gitee.io/v2/docs/ 3.引入 官网地址: https://layui.gitee.io/v2/ 引入(在官网下载,)jquery-1.7.2.min.js,layui/layui.js **<link href"js/layui/css/layui.css" rel"stylesh…...
OPPO哲库事件 “ 始末 ” ! 集体打哑谜?
1►OPPO哲库解散 2019 年,美国商务部以“科技网络安全”为由,将华为公司及其70家附属公司列入出口管制“实体名单”。与此同时,OPPO 创始人兼 CEO陈明永对外宣布,公司将为未来三年内投入 500 亿元用于前沿技术和深水区技术的探索…...

数据聚类分析
K均值 1.1 数据来源(随机生成) import matplotlib.pyplot as plt from sklearn.datasets import make_blobsX, y make_blobs(n_samples150,n_features2,centers3,cluster_std0.5,shuffleTrue,random_state0) # plt.scatter(X[:, 0], X[:, 1], cwhite, markero, edgecolorsbl…...

前 40 个 Microsoft Excel 面试问题答案
1)什么是 Microsoft Excel? Microsoft Excel 是一个电子电子表格应用程序,使用户可以使用按行和列细分的电子表格系统,使用公式存储,组织,计算和处理数据。 它还提供了使用外部数据库进行分析,…...

ros2学习笔记:shell环境变量脚本setup.bash[-z][-n][-f]参数作用
-n作用 [ -n 字符串 ] or [ 字符串 ] 字符串的长度为非零(有内容)则为真。加-n与不加-n结果相同。 -z作用 [ -z 字符串 ] 字符串的长度为零则为真。 字符串为空即NULL时为真,与上面的-n相反。 -f作用 [ -f FILE ] 如果 FILE 存在且是一…...

xss渗透(跨站脚本攻击)
一、什么是XSS? XSS全称是Cross Site Scripting即跨站脚本,当目标网站目标用户浏览器渲染HTML文档的过程中,出现了不被预期的脚本指令并执行时,XSS就发生了。 这里我们主要注意四点: 1、目标网站目标用户; 2、浏览…...
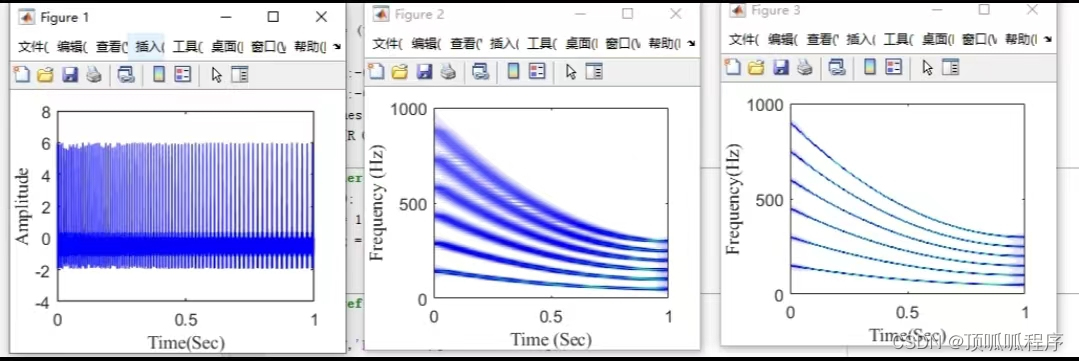
9参数化重采样时频变换,基于MATLAB平台,程序已调通,可直接替换数据进行分析。
参数化重采样时频变换,基于MATLAB平台,程序已调通,可直接替换数据进行分析。 9matlab参数化重采样时频变换 (xiaohongshu.com)...
RK3568平台开发系列讲解(调试篇)系统运行相关频率设置
🚀返回专栏总目录 文章目录 一、CPU 频率设置二、DDR 频率设置三、NPU 频率设置沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 CPU 默认是 interactive 状态,它会根据 CPU 使用率和目标负载来动态地调整 CPU 频率。为获得更高运行速度或者性能评估,我们需要手动固…...

嵌入式:驱动开发 Day2
作业:字符设备驱动,完成三盏LED灯的控制 驱动代码: mychrdev.c #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/uaccess.h> #include <linux/io.h> #include &q…...
RK3399平台开发系列讲解(入门篇)VIM的基础命令
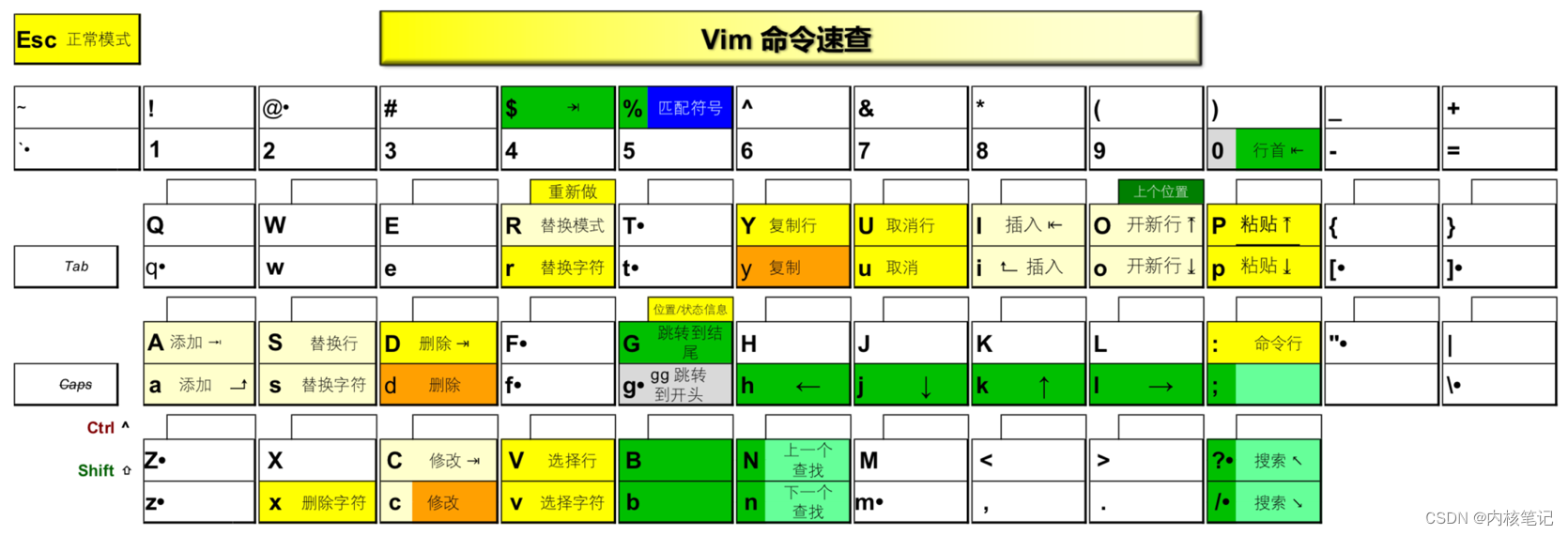
🚀返回专栏总目录 文章目录 一、Vim 命令速查二、其他命令三、Vim模式沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 本篇将介绍Vim相关命令。 一、Vim 命令速查 简单说明一下,这张图上展示了一个键盘。图中的“•”表示,单个字母不是完整的命令,必须再有进一步…...

Rocky Linux 安装图解(替代centos)服务器+桌面
centos自从20年底转变为不稳定版本后,有很多替代方案 经过近3年的发展,rocky linux算是一个比较好的选择,一是依照red hat企业版来做,二是rocky的发起者也是centos的创始人 如果想安装debian,可以参考:deb…...

webpack 基础配置
常见配置 文件打包的出口和入口webpack如何开启一台服务webpack 如何打包图片,静态资源等。webpack 配置 loader配置 plugin配置sourceMap配置 babel 语法降级等 接下来 , 我们先从webpack的基本配置 开始吧! 在准备 配置之前 , 搭建一个 …...
C语言和mfc按格式读取文件数据
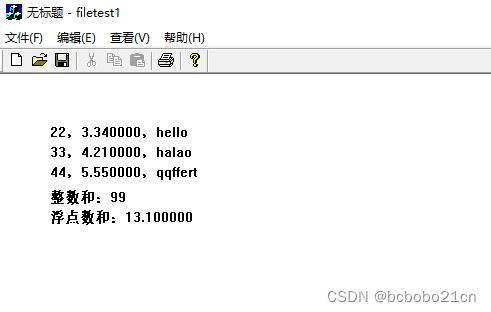
fscanf()函数的功能是从文件中按格式读取一个或多个数据; 例如文件中有一行数据, 22 3.34 hello 则使用 fscanf(fp, "%d%f%s", &a, &f, str) 可一次读取整型、浮点、字符串三个数据; 此函数位于C标准库头文件<stdio…...
)
SQLyog 各版本下载与安装(目前最新版本为13.2.0)
文章目录 一、SQLyog Ultimate 各版本下载1. For Windows x642. For Windows x86 二、SQLyog Community 各版本下载1. For Windows x642. For Windows x863. For Linux x86_644. For Linux i386 三 、SQLyog 安装四、如何解决SQLyog试用期到期问题五、最后 数据库可视化工具&am…...

CopyOnWrite 容器
CopyOnWrite容器是Java并发包中提供的一种特殊类型的集合,它的特点是在进行修改操作时不会修改原始容器,而是创建一个新的容器副本进行修改,这样可以避免并发修改异常(ConcurrentModificationException)。 主要的CopyOnWrite容器包括: CopyOnWriteArrayList:这是一个基…...

云服务部署:AWS、Azure和GCP比较
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Linux安装Ansible管理工具
条件情况说明 准备4台机器,是单master集群安装 192.168.186.128 ansible 192.168.186.129 node1 192.168.186.130 node2 192.168.186.131 node3 #永久修改主机名 hostnamectl set-hostname ansible && bash #在ansible上操作 hostnamectl set-hostname n…...
七天学会C语言-第二天(数据结构)
1. If 语句: If 语句是一种条件语句,用于根据条件的真假执行不同的代码块。它的基本形式如下: if (条件) {// 条件为真时执行的代码 } else {// 条件为假时执行的代码 }写一个基础的If语句 #include<stdio.h> int main(){int x 10;…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
