排序算法-插入排序
属性
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结: 1. 元素集合越接近有序,直接插入排序算法的时间效率越高 2. 时间复杂度:O(N^2) 3. 空间复杂度:O(1),它是一种稳定的排序算法 4. 稳定性:稳定
代码及其注释
public class InsertSort {// 插入排序public static void insertSort(int[]arr){//首先比较第一个元素和第二个元素之间的大小关系,所以i从1开始for(int i=1;i<arr.length;i++){//将要进行比较的数放到一个临时变量中,此时就相当于i位置现在是空的int tmp=arr[i];//遍历i前面的数据,与temp中的数据进行比较int j=i-1;for(;j>=0;j--){//要是i前面的数据比i的数据大,就说明该数据应该在i数据之前,就将该数据向前移if(arr[j]>tmp){arr[j+1]=arr[j];}//i前面的数据比i的数据小了,找到了合适的位置,就退出循环并将i的数据放到当前遍历到的j数据之前else {break;}}//这里有特殊情况,当i前面的数据都比i大时,j的取值会一直取到-1,退出循环,此时就需要将i的值放到0的位置arr[j+1]=tmp;}}
}相关文章:

排序算法-插入排序
属性 当插入第i(i>1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移 直接插入排序…...
数码管显示)
多位数按键操作(闪烁)数码管显示
/*----------------------------------------------- 内容:按键加减数字,多个数码管显示 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存…...

MyEclipse项目导入与导出
一、项目导出 1、右键选择项目名称,弹出菜单中选择“export”,如下图所示 2、选择“恶心“export”,弹出菜单如下;在“General“选项中,选择“File System”选项 3、点击“next”,进入保存位置选择界面&am…...
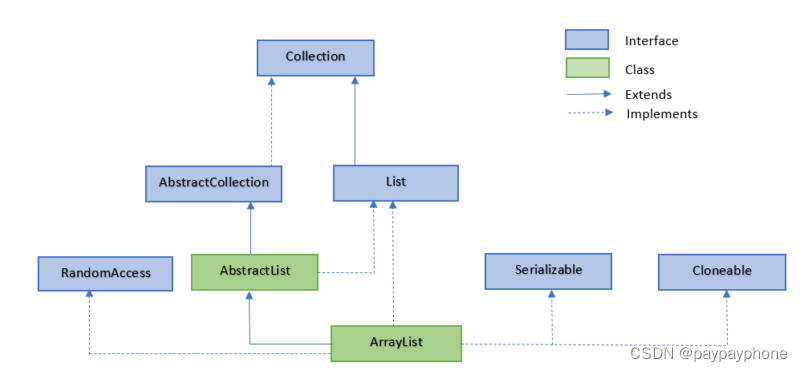
ArrayList和LinkedList
最近在刷回溯算法时,遇见了List<Integer> A new ArrayList<>(); LinkedList<Integer> B new LinkedList<>();这类型的表达方式 很好奇的问题是: 1、List<Integer> A new ArrayList<>();为什么是正确的写法 2…...

Linux 配置 Nginx 服务完整详细版
目录 前言 配置Nginx监听端口和服务器块 # 防DDoS配置 # 日志配置 # 设置服务器块 监听端口 网站根目录 默认文件 静态文件目录 图像文件目录 # 自定义错误页面 # 反向代理配置 # 配置SSL/TLS 1、获取SSL/TLS证书 2、安装证书 3、配置SSL/TLS # 配置SSL协议版本…...
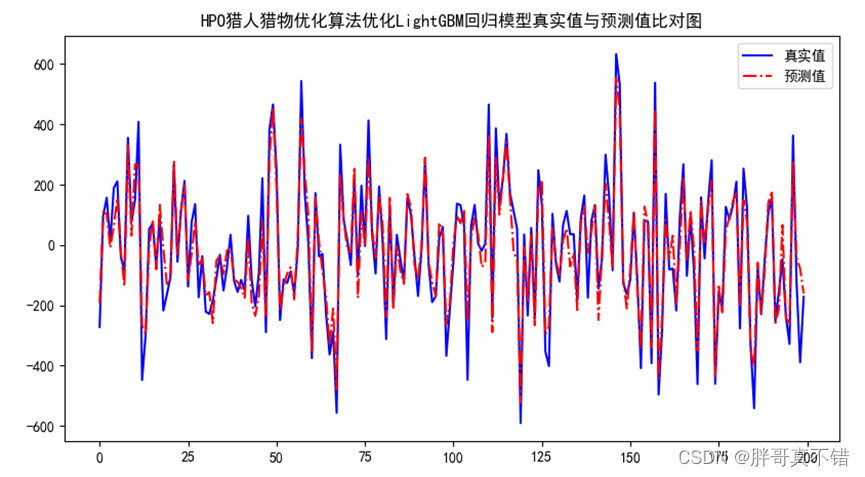
Python实现猎人猎物优化算法(HPO)优化LightGBM回归模型(LGBMRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的…...

无涯教程-JavaScript - ODD函数
描述 ODD函数返回四舍五入到最接近的奇数整数的数字。 ODD函数是Excel中的15个舍入函数之一。 语法 ODD (number)争论 Argument描述Required/OptionalNumberThe value to round.Required Notes 无论数字的符号如何,值都将从零舍入到下一个奇数。如果number是一个奇数整数…...

Easyui里的datagrid嵌入select下拉框
问题: 想使用datagird里嵌入select下拉框,并在提交form表单时获取datagrid选中的每行数据里的每个下拉框选中的值。 解决方案: 其中economicIssuesSelect使用下拉框,重点关注 initEconomicIssues(row)方法。这里的方法需要传递ro…...

计算机专业毕业设计项目推荐03-Wiki系统设计与实现(JavaSpring+Vue+Mysql)
Wiki系统设计与实现(JavaSpringVueMysql) **介绍****系统总体开发情况-功能模块****各部分模块实现** 介绍 本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设…...

微服务的艺术:构建可扩展和弹性的分布式应用
文章目录 什么是微服务架构?微服务的设计原则1. 基于业务边界划分服务2. 松耦合和强内聚3. 自动化测试和部署4. 监控和日志5. 弹性设计 微服务的实施细节1. 服务发现示例代码:使用Consul进行服务发现 2. 负载均衡示例代码:Nginx配置负载均衡 …...

在PHP8中对数组进行排序-PHP8知识详解
在php8中,提供了丰富的排序函数,可以对数组进行排序操作。常见的排序函数如下几个:sort() 函数、rsort() 函数、asort() 函数、arsort() 函数、ksort() 函数、krsort() 函数、natsort()函数和natcascsort()函数。 1、sort() 函数:…...

Redis混合模式持久化原理
前言 前面文章中我们也介绍过Redis的持久化方式有两种:rdb持久化和aof持久化,具体详情可查看之前文章redis持久化。rdb持久化还是aof持久化它们都有各自的缺点。 rdb和aof缺点 rdb持久化:由于是定期对内存数据快照进行持久化,因此…...
)
《BPF Performance Tools —— 洞悉Linux系统和应用性能》学习笔记 —— 第一章 介绍(2)
接前一篇文章:《BPF Performance Tools —— 洞悉Linux系统和应用性能》学习笔记 —— 第一章 介绍(1) 1.2 Tracing、Snooping、Sampling、Profiling和Observability是什么? 这些都是用于对分析技术和工具进行分类的术语。 Trac…...
)
【计算机网络】网络编程接口 Socket API 解读(7)
Socket 是网络协议栈暴露给编程人员的 API,相比复杂的计算机网络协议,API 对关键操作和配置数据进行了抽象,简化了程序编程。 本文讲述的 socket 内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解 socket 编程。…...

crypto++下载、安装(VS2017)及加解密使用
crpto 下载按个人喜好下载,我使用了图中框选的8.8.0 Release.解压 安装打开修改以适应本机配置整理至标准库 调用加解密使用 Crypto(也称为Crypto Library或Crypto STL)是一个C密码学库,它提供了各种密码学算法和安全编程工具&…...
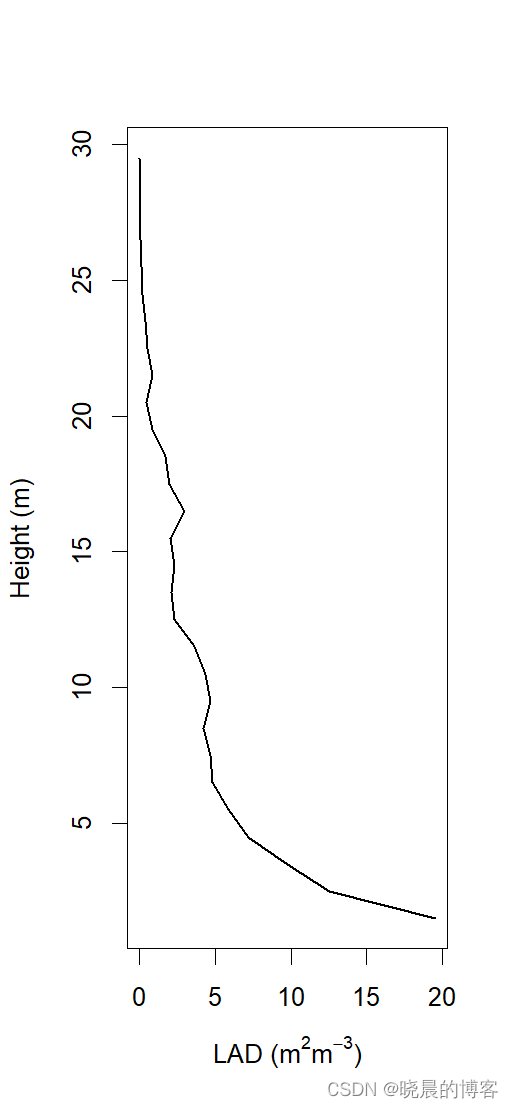
R语言画图
简单记录一下 plot(lad_profile_relative$lad, lad_profile_relative$height, type"l", lwd1.5, xlabexpression(paste("LAD ", "(", m^2, m^-3, ")" )), ylab"Height (m)")X轴数据, Y轴数据 type, 标记类型 lw…...
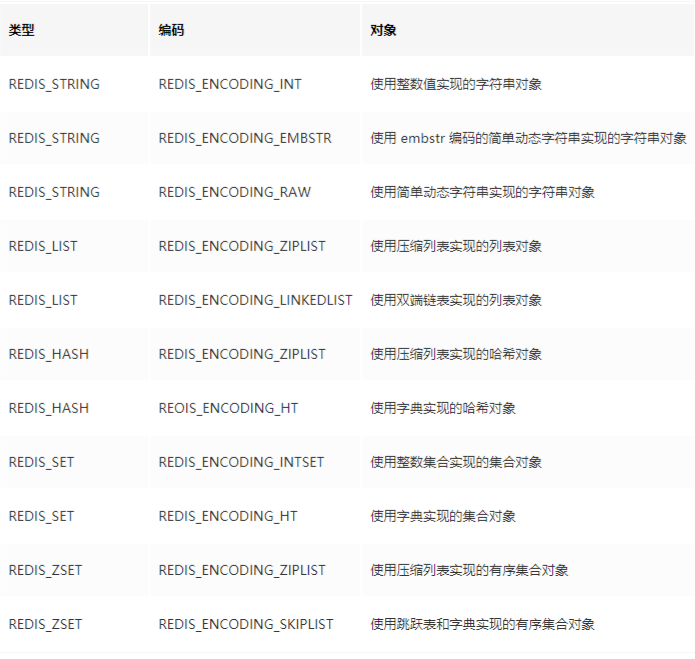
redis 核心数据结构
一、简述 redis是一个开源的使用C语言编写的一个kv存储系统,是一个速度非常快的非关系远程内存数据库。它支持包括String、List、Set、Zset、hash五种数据结构。 除此之外,通过复制、持久化和客户端分片等特性,用户可以很方便地将redis扩展…...
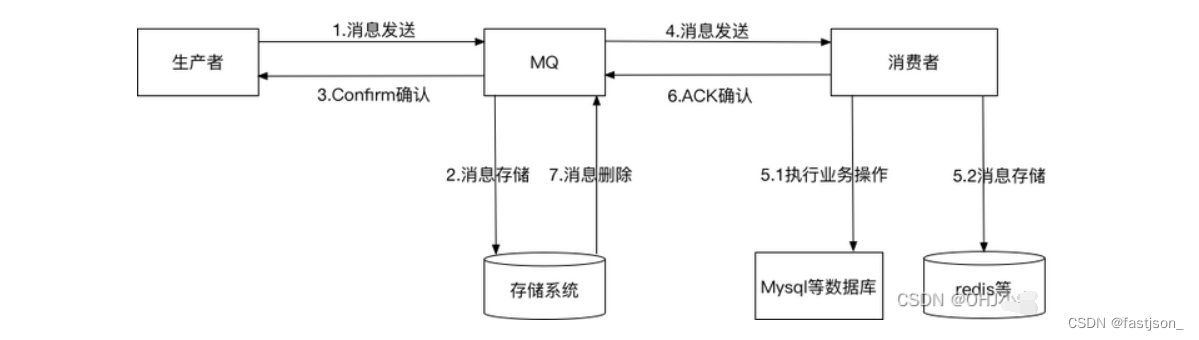
RabbitMQ消息可靠性(一)-- 生产者消息确认
前言 在项目中,引入了RabbitMQ这一中间件,必然也需要在业务中增加对数据安全性的一层考虑,来保证RabbitMQ消息的可靠性,否则一个个消息丢失可能导致整个业务的数据出现不一致等问题,对系统带来巨大的影响,…...

9 种方法使用 Amazon CodeWhisperer 快速构建应用
Amazon CodeWhisperer 是一款很赞的生成式人工智能编程工具。自从在工作中使用了 CodeWhisperer,我发现不仅代码编译的效率有所提高,应用开发的工作也变得快乐起来。然而,任何生成式 AI 工具的有效学习都需要初学者要有接受新工作方式的心态和…...
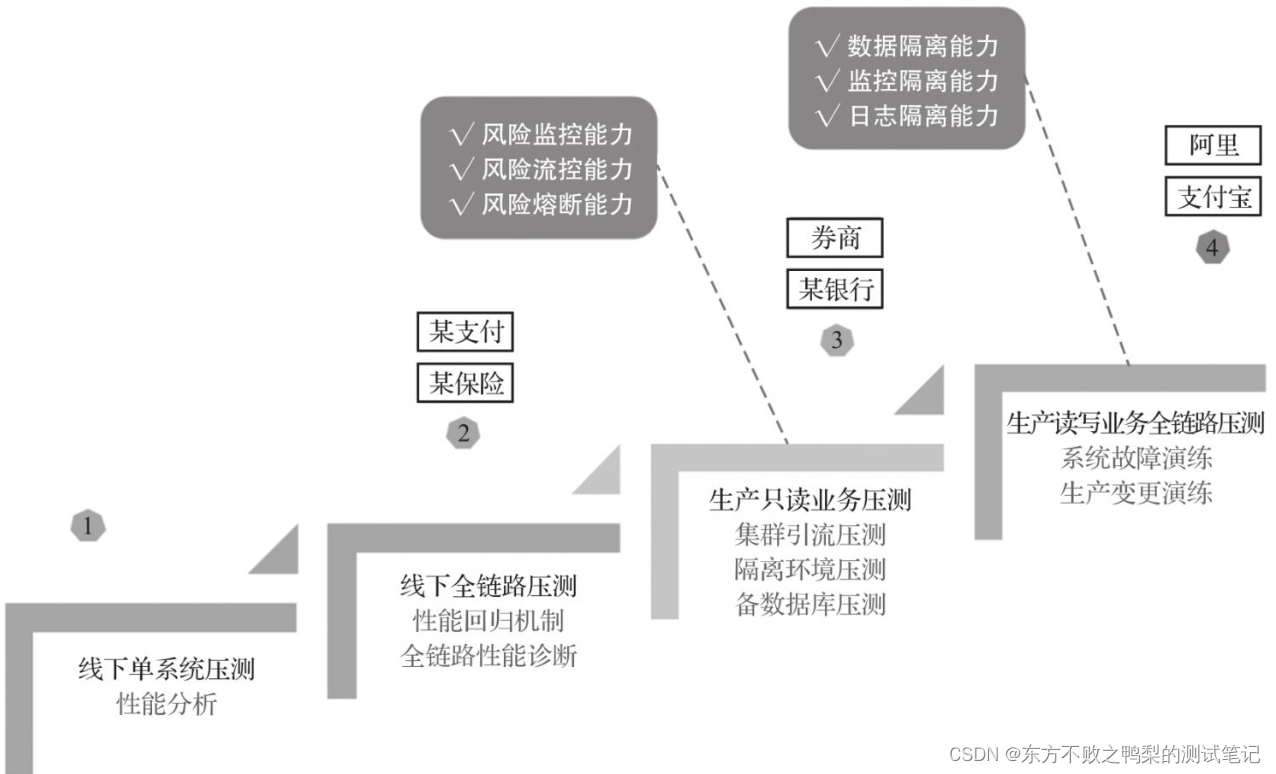
性能测试-性能工程落地的4个阶段(21)
性能工程按照不同的内容和目的划分为4个阶段,分别是线下单系统压测分析阶段、线下全链路压测分析阶段、生产只读业务压测及容量评估阶段、生产读写业务全链路压测及容量评估阶段。(也可以理解为一个企业性能测试体系的发展阶段) 线下单系统压测分析阶段 针对单系统的性能…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
