【Davinci开发】：开发过程问题记录及总结
相关文章：
【Davinci开发】：开发过程问题记录及总结
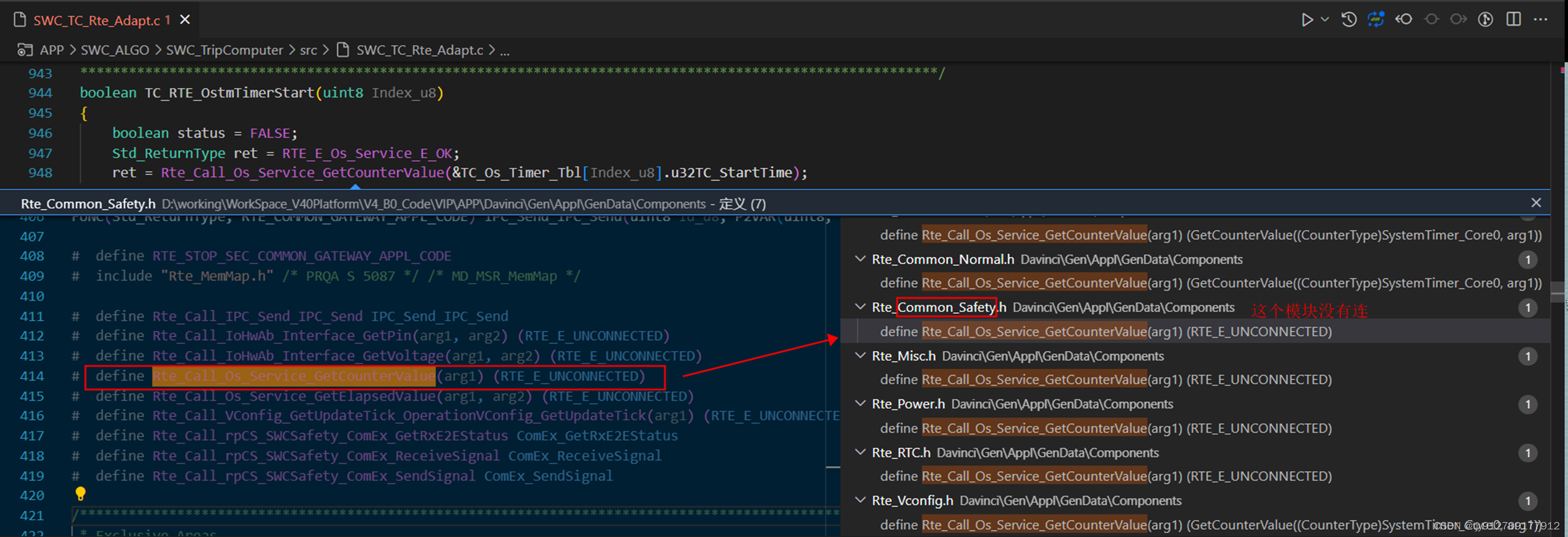
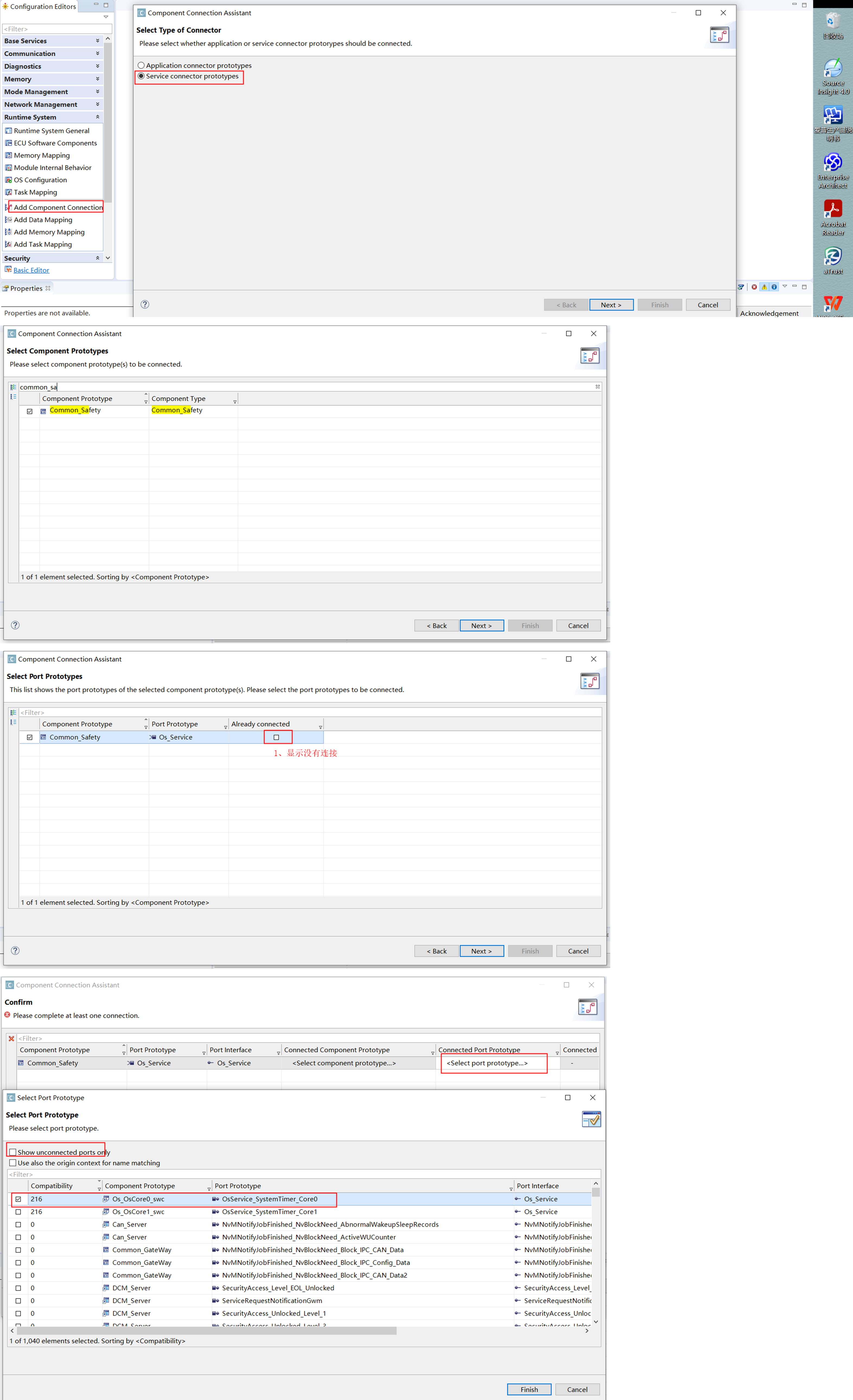
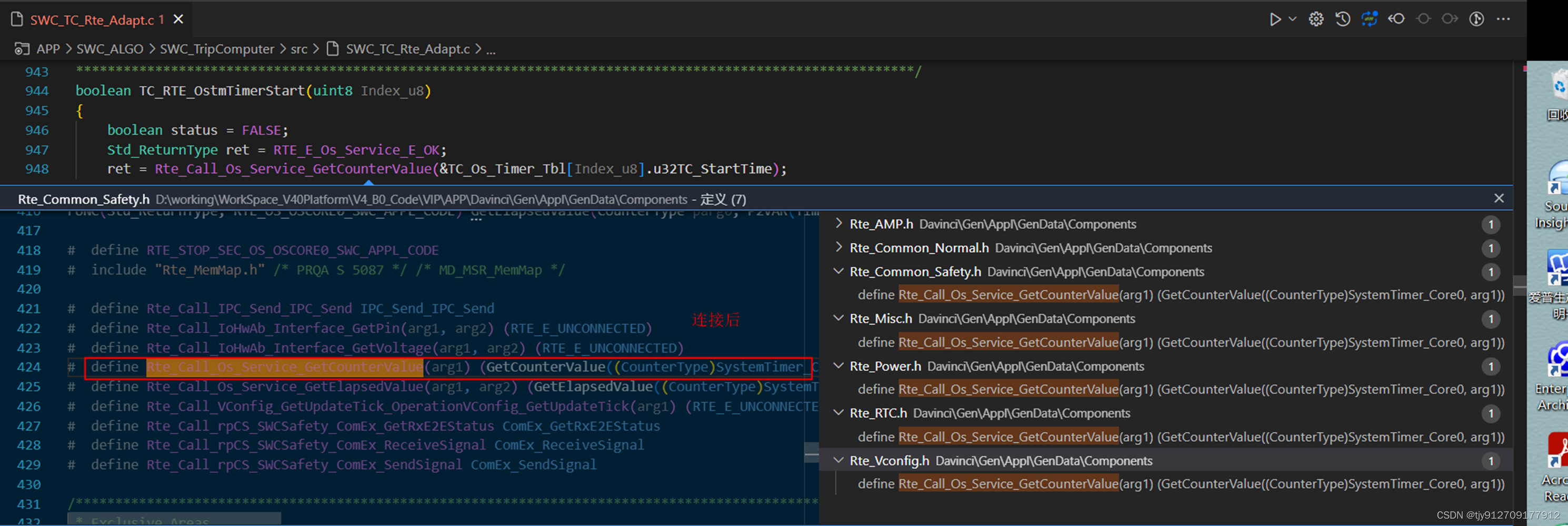
开发过程问题总结 1、SWC访问系统OS Timer返回值异常a、代码发现，RTE接口为未连接状态b、连接后，仍然有问题，单步调试，发现没有访问权限当新平台基于之前平台的代码而延续开发时（应用代码相同，但是芯片已经更换），记录开发过程中遇所到的问题，单步调试，逐一排查。 1、…...
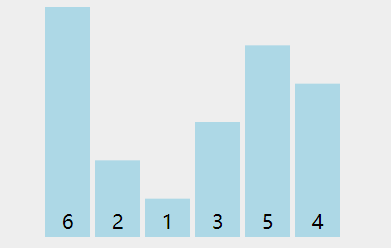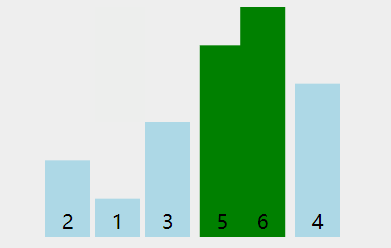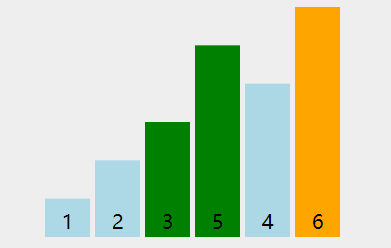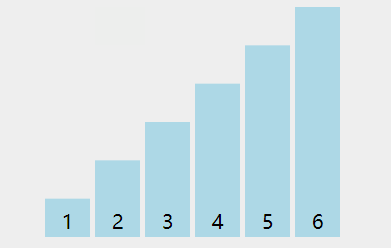
数据结构——排序算法——冒泡排序
冒泡排序1 void swap(vector<int> arr, int i, int j) {int temp arr[i];arr[i] arr[j];arr[j] temp;}void bubbleSort1(vector<int> arr) {for (int i 0; i < arr.size() - 1; i){for (int j 0; j < arr.size() - 1 - i; j){if (arr[j] > arr[j 1…...
vscode使用
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么？二、使用步骤 1.引入库2.读入数据总结 前言 提示：这里可以添加本文要记录的大概内容： 例如：…...
python经典百题之求前！的和
题目：求12!3!…20!的和 方法一： 使用for循环和阶乘函数计算每项的值，再将每项的值累加起来。 def factorial(n):if n 0:return 1else:return n * factorial(n-1)sum 0 for i in range(1, 21):sum factorial(i) * iprint(sum)优点&#…...
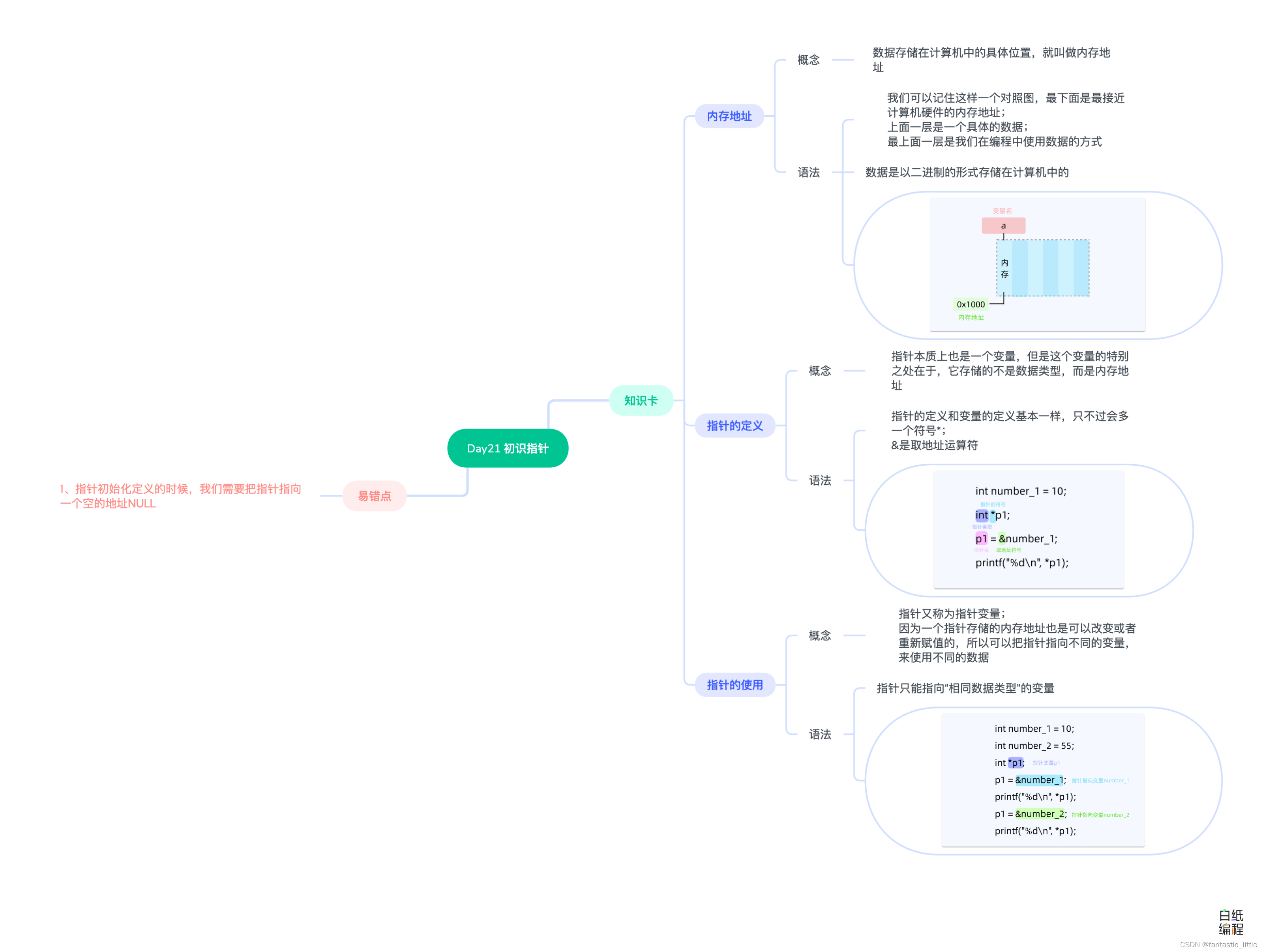
C语言入门Day_22 初识指针
目录 前言： 1.内存地址 2.指针的定义 3.指针的使用 4.易错点 5.思维导图 前言： 之前我们学过变量可以用来存储数据，就像一个盒子里面可以放不同的球一样。 这是一个方便大家理解专业概念的比喻。 在计算机世界里面，数据实…...
【面试必刷TOP101】删除链表的倒数第n个节点 两个链表的第一个公共结点
目录 题目：删除链表的倒数第n个节点_牛客题霸_牛客网 (nowcoder.com) 题目的接口： 解题思路： 代码： 过啦！！！ 题目：两个链表的第一个公共结点_牛客题霸_牛客网 (nowcoder.com) …...
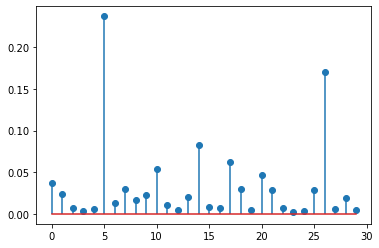
手刻 Deep Learning -第壹章 -PyTorch教学-激励函数与感知机入门（上）
一、前言 本文接续前篇教学 Pytorch 与线性回归 ，本文着重在 Activation Function （ 中文称 激励函数 ），我们会介绍激励函数 （也有人称 激活函数？ 激发函数？ ） 为什么会有用…...
物理内存分配
目录 内核物理内存分配接口 内存分配行为（物理上） 内存分配的行为操作 内存 三个水位线 水线计算 水位线影响内存分配行为 内存分配核心__alloc_pages 释放页 1、内核物理内存分配接口 struct page *alloc_pages(gfp_t gfp, unsigned int ord…...
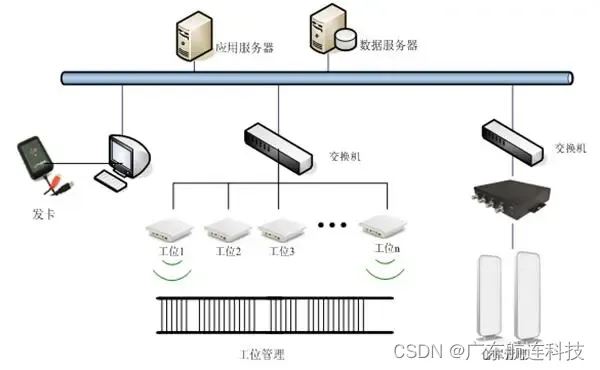
RFID产线自动化升级改造管理方案
应用背景 在现代制造业中，产线管理是实现高效生产和优质产品的关键环节，产线管理涉及到生产过程的监控、物料管理、工艺控制、质量追溯等多个方面，有效的产线管理可以提高生产效率、降低成本、改善产品质量，并满足市场需求的变化…...
全量数据采集：不同网站的方法与挑战
简介 在当今数字化时代中，有数据就能方便我们做出很多决策。数据的获取与分析已经成为学术研究、商业分析、战略决策以及个人好奇心的关键驱动力。本文将分享不同网站的全量数据采集方法，以及在这一过程中可能会遇到的挑战。 部分全量采集方法 1. 撞店…...
Redis——渐进式遍历和数据库管理命令
介绍 如果使用keys * 这样的操作，将Redis中所有的key都获取到，由于Redis是单线程工作，这个操作本身又要消耗很多时间，那么就会导致Redis服务器阻塞，后续的操作无法正常执行 而渐进式遍历，通过多次执行遍历…...
如何打造可视化警务巡防通信解决方案
近年来，科学技术飞速发展，给予了犯罪分子可乘之机。当面临专业化的犯罪分子、高科技的犯罪手段，传统警务模式似乎不能满足警方打击犯罪的需要，因此当今公安工作迫切需要构建智能化、系统化、信息化的警务通信管理模式。 警务人员…...
ATF(TF-A) SPMC威胁模型-安全检测与评估
安全之安全(security)博客目录导读 ATF(TF-A) 威胁模型汇总 目录 一、简介 二、评估目标 1、数据流图 三、威胁分析 1、信任边界 2、资产 3、威胁代理 4、威胁类型 5、威胁评估 5.1 端点在直接请求/响应调用中模拟发送方或接收方FF-A ID 5.2 篡改端点和SPMC之间的…...
BIO AIO NIO 的区别
BIO AIO NIO 是 Java 中用于 I/O 操作的三种不同的编程模型。它们的区别在于它们执行I/O 操作的方式和效率。在讲 BIO,NIO,AIO 之前先来回顾一下这样几个概念：同步与异步，阻塞与非阻塞。 同步与异步 同步：同步就是发起一个调用后ÿ…...
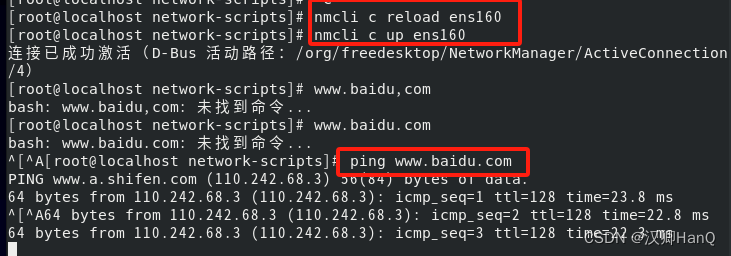
大数据学习1.1-Centos8网络配置
1.查看虚拟网卡 2.配置网络信息 打勾处取消 记住箭头的数字 3.修改 网络连接 4.进入虚拟网络 5.进入属性 6.修改IPv4 5.将iIP和DNS进行修改 6.配置网络信息-进入修改网络配置文件 # 进入root用户 su root # 进入网络配置文件 cd /etc/sysconfig/network-scripts/ # 修改网络配…...
在Android studio 创建Flutter项目运行出现问题总结
在Android studio 中配置Flutter出现的问题 A problem occurred configuring root project ‘android’出现这个问题。解决办法 首先找到flutter配置的位置 在D:\xxx\flutter\packages\flutter_tools\gradle位置中的flutter.gradle buildscript { repositories { googl…...
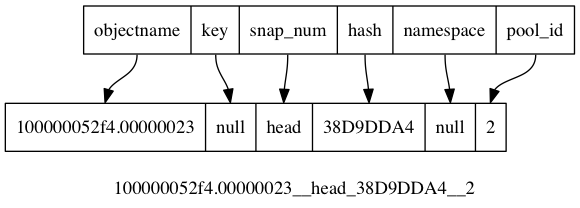
Ceph入门到精通-ceph对于长文件名如何处理
RADOS object with short name 上一篇博文，我们将介绍了对象相关的数据结构ghobject_t，以及对象在底层文件系统存储的文件名，以及如何从文件名对应到 ghobject_t对象。 映射关系如下图所示： 这里面有一个漏洞，即obje…...
vue+element-ui 项目实战示例详解【目录】
vue 和 element是两个流行的前端即时，通常用于管理后台，PC等页面 能够快速构建美观的界面 1. vue2 介绍 Vue.js是一个流行的JavaScript框架，用于构建用户界面。它的版本分为Vue 2和Vue 3，而Element是一个基于Vue.js 2的UI组件库。…...
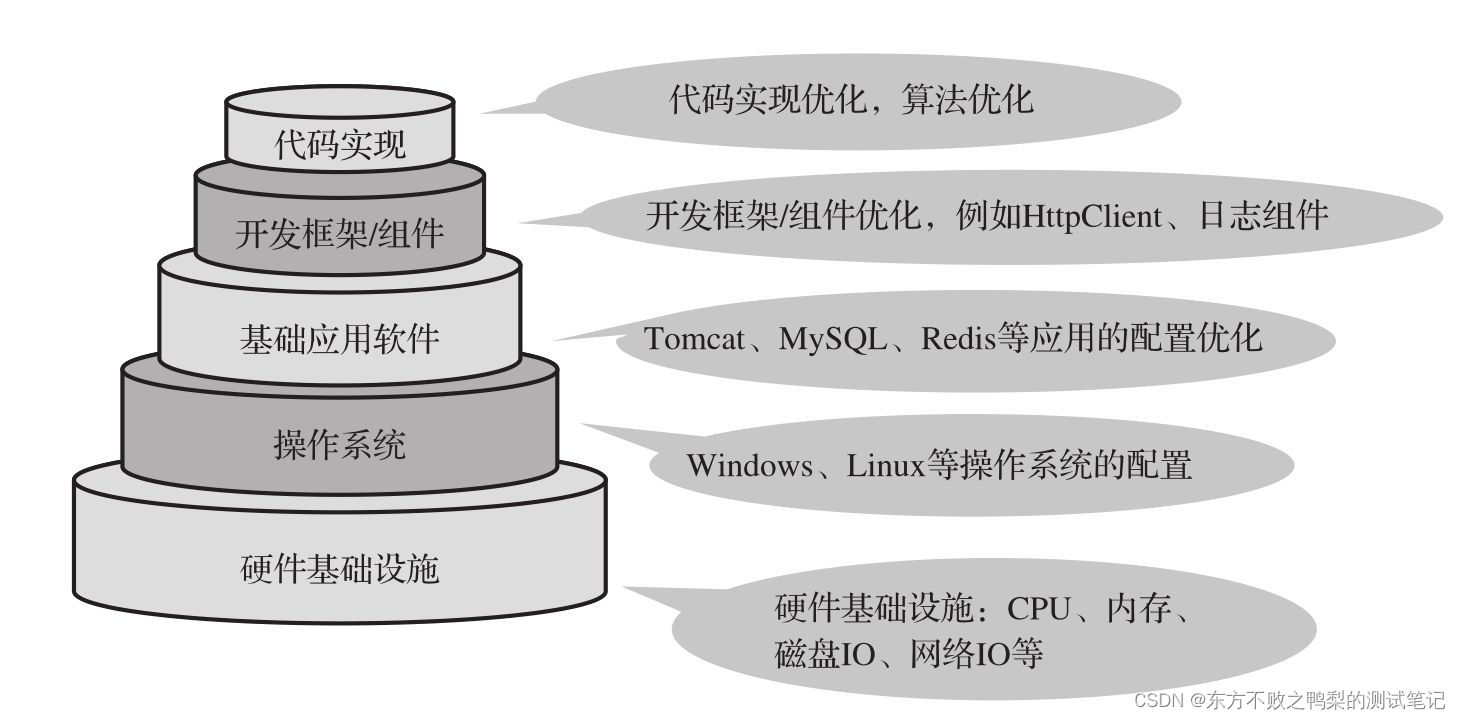
性能测试-性能调优主要方向和原则（15）
性能调优主要方向明确性能瓶颈之后，就需要进行性能调优了，调优主要从图所示的多个方向入手。能优化手段并不一定是独立应用的，在一次优化过程中很可能应用了多种优化技巧。 硬件层面优化 硬件层面优化更偏向于监控，当定位到硬件资源成为瓶颈后，更多是采用扩容等手段来解决…...
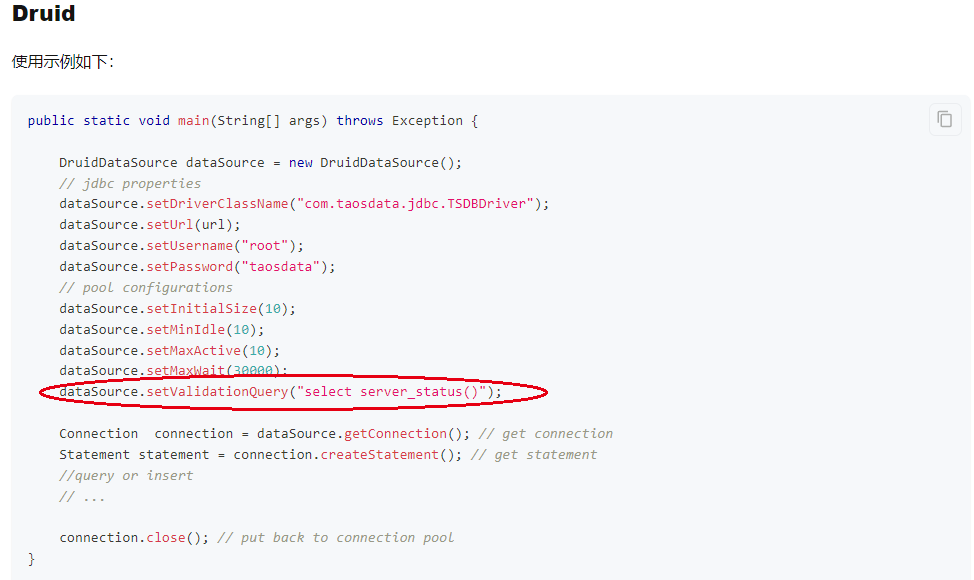
关于taos数据库使用过程中突发“unable to establish connection”问题解决
项目使用的版本信息 1.taos的版本信息 3.0.4.1 2.jdbc的版本 3.2.1 3.druid连接池版本 1.2.11问题描述 Java应用服务连接，突然大量抛出如下的异常信息导致应用宕机： sql: select server_status(), desc: unable to establish connection和集团DBA沟通…...
基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
理解 MCP 工作流：使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP？ 模型控制协议 (MCP) 是一种创新的协议，旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议，它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求，由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面： 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限，形成层级清晰的管理网络…...
React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程
本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习视频及资料，尽在聚客AI学院。 本文全面剖析RNN核心原理，深入讲解梯度消失/爆炸问题，并通过LSTM/GRU结构实现解决方案，提供时间序列预测和文本生成…...
Go 语言并发编程基础：无缓冲与有缓冲通道
在上一章节中，我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道，它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...