二叉树实现的相关函数
1.二叉树的创建
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{ if (n==0||a[*pi] == '#'){ (*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->_data = a[(*pi)++];root->_left = BinaryTreeCreate(a, --n, pi);root->_right = BinaryTreeCreate(a, --n, pi);return root;}形参中BTDataType* a是自定义类型的数组,用与给二叉树的结点赋值,int n是数组元素的个数,int*pi是当前将要放入二叉树的元素的下标。本方法适用于用前序遍历的结果来创建二叉树。若采用别的遍历方式需修改代码中调用函数和数组赋值的位置。
2.二叉树的销毁
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{if (root == NULL){return;}if ((*root)->_left){free((*root)->_left);(*root)->_left = NULL;}if ((*root)->_right){free((*root)->_right);(*root)->_right = NULL;}free(*root);*root = NULL;return;
}
销毁采用后序遍历的方式,先销毁结点的左右子树,再销毁当前结点。若先销毁当前结点,无法找到该结点的左右子树的位置。
3.求二叉树结点的个数
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;}
采用后续遍历的方式,求出当前结点的左右子树的结点个数,相加后再加上当前结点(+1的由来)。
4.求叶子结点的个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left==NULL && root->_right==NULL){return 1;}return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);}叶子结点是左右子树都为空且自己本身不为空的结点,由于此处需要通过访问左右子树来判断,所以在这之前必须判断当前结点是否为空。在当前结点有子结点的时候,则访问子树,返回子树的叶子结点个数。
5.求第k层结点的个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);}对当前结点的第k层,就是对当前结点的子节点的第k-1层。对于结点为空的判断和对层的判断先后顺序不能修改,因为可能会有k==1的时候是空结点的情况,此时不应该加1.(即k=2的时候恰好是叶子结点的情况)
6.查找值为x的结点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->_data == x){return root;}BTNode* left = BinaryTreeFind(root->_left, x);if (left != NULL){return left;}return BinaryTreeFind(root->_right, x);}通过先序遍历的方式遍历所有结点,找到值符合的就返回,都不符合的时候返回NULL。
此处判断左子树是否为空不判断右子树的原因是此时左子树已经为空,若右子树有则返回右子树,若右子树为空则返回右子树(也是空结点)。
7.层序遍历
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{queue<BTNode*> q;if (root == NULL){ return;}q.push(root); while (!q.empty()){BTNode* tmp = q.front();printf("%c ", tmp->_data);q.pop();if (tmp->_left){q.push(tmp->_left);}if (tmp->_right){q.push(tmp->_right);}}printf("\n");return;}思路:通过队列先进先出的特性,使得当前队列中恒保持只有相邻两层或只有一层的结点的情况。
8.判断是否是满二叉树
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{queue<BTNode*> q;if (root == NULL){return 1;}int count = 0;q.push(root);while (!q.empty()){BTNode* tmp = q.front();q.pop();if (tmp->_left&&count==0){q.push(tmp->_left);}else if (tmp->_left && count == 1){return 0;}else if(tmp->_left==NULL&&count==0){count = 1;}if (tmp->_right&&count==0){q.push(tmp->_right);}else if (tmp->_right && count == 1){return 0;}else if (tmp->_right == NULL && count == 0){count = 1;}}return 1;}满二叉树的特性就是层序遍历的情况下,出现一次结点为空以后,就不会再有结点不为空的情况,此处用count=1表示第一次遇到结点为空,此后存在两种情况,一种是后面的结点全是空,最后队列为空退出,此时是满二叉树。一种情况是后面又遇到非空结点,由于此时count已经等于1了,则不是满二叉树。
相关文章:

二叉树实现的相关函数
1.二叉树的创建 BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) { if (n0||a[*pi] #){ (*pi);return NULL;}BTNode* root (BTNode*)malloc(sizeof(BTNode));root->_data a[(*pi)];root->_left BinaryTreeCreate(a, --n, pi);root->_right Binary…...
)
Redis面试题(二)
文章目录 前言一、Redis 支持的 Java 客户端都有哪些?官方推荐用哪个?二、Redis 和 Redisson 有什么关系?三、Jedis 与 Redisson 对比有什么优缺点?四、说说 Redis 哈希槽的概念?五、Redis 集群的主从复制模型是怎样的…...

STP介绍
目录 STP概述 二层环路带来的问题 1.广播风暴 2.MAC地址漂移问题 3.多帧复制---这个好理解,同一个数据帧被重复收到多次,被称为多帧复制。 802.1D生成树 STP的BPDU BPDU主要分为两大类 配置BPDU RPC COST 配置BPDU的工作过程 TCN BPDU TCN…...

numpy 和 tensorflow 中的各种乘法(点乘和矩阵乘)
嗨喽,大家好呀~这里是爱看美女的茜茜呐 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备好了,直接在文末名片自取就可 点乘和矩阵乘…...

(图论) 1020. 飞地的数量 ——【Leetcode每日一题】
❓ 1020. 飞地的数量 难度:中等 给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个 海洋单元格、1 表示一个 陆地单元格。 一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边…...

c++ 重载、重写、覆盖
重载:指在同一作用域内,有多个同名但参数不同的函数的现象,叫重载;可以是任何用户定义的函数,例如 类成员函数、类静态函数、普通函数重写:子类重写父类的同名函数,只要子类出现有父类的同名函数…...
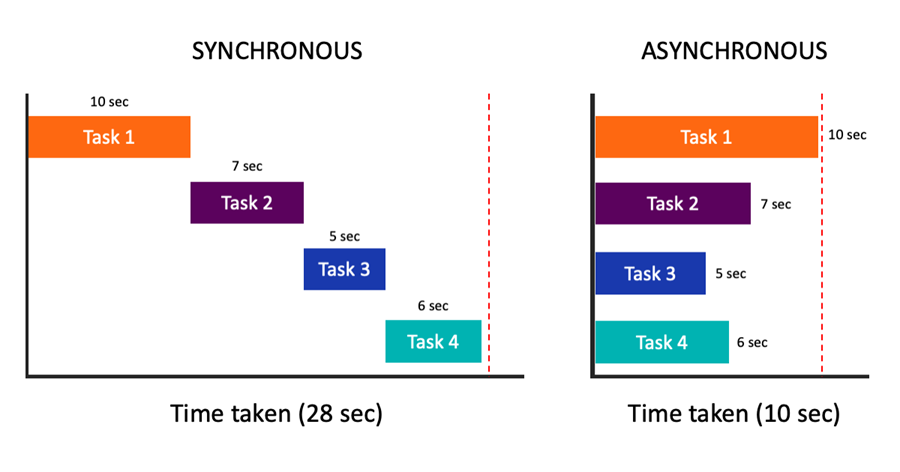
Python异步编程高并发执行爬虫采集,用回调函数解析响应
一、问题:当发送API请求,读写数据库任务较重时,程序运行效率急剧下降。 异步技术是Python编程中对提升性能非常重要的一项技术。在实际应用,经常面临对外发送网络请求,调用外部接口,或者不断更新数据库或文…...
SpriteKit与Swift配合:打造您的第一个简易RPG游戏的步骤指南
1. 简介: RPG(Role-Playing Game)游戏是一种角色扮演游戏,它允许玩家在一个虚拟的游戏世界中扮演一个或多个角色。在本教程中,我们将使用Apple的2D游戏框架SpriteKit和Swift编程语言来创建一个简单的RPG游戏。我们将从…...

服务网格的面临挑战:探讨服务网格实施中可能遇到的问题和解决方案
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

leetcode61 旋转链表
题目 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 输入:head [1,2,3,4,5], k 2 输出:[4,5,1,2,3] 解析 这道题属实不好想:需要计算出链表的长度,然后在k > n的…...
【学习笔记】各类基于决策单调性的dp优化
文章目录 对于决策单调性的一般解释关于决策单调性的证明四边形不等式一维dp区间dp一种二维dp一些满足四边形不等式的函数类 与图形相结合 决策单调性的常见优化手段二分队列二分栈分治类莫队做法 SMAWKWQS二分WQS多解情况满足四边形不等式的序列划分问题的答案凸性以及WQS二分…...
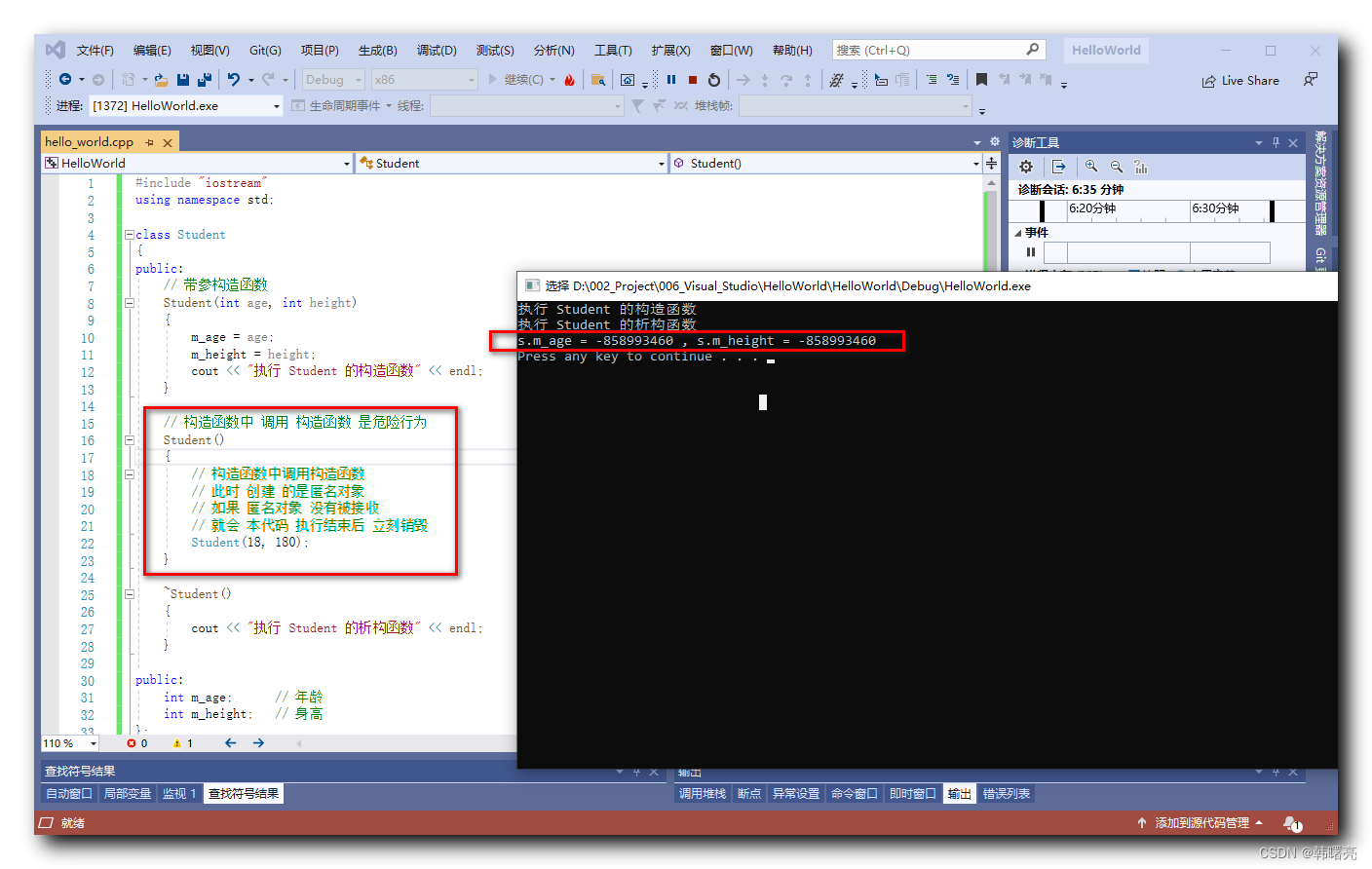
【C++】构造函数初始化列表 ⑤ ( 匿名对象 生命周期 | 构造函数 中 不能调用 构造函数 )
文章目录 一、匿名对象 生命周期1、匿名对象 生命周期 说明2、代码示例 - 匿名对象 生命周期 二、构造函数 中调用 构造函数1、构造函数 中 不能调用 构造函数2、代码示例 - 构造函数中调用构造函数 构造函数初始化列表 总结 : 初始化列表 可以 为 类的 成员变量 提供初始值 ;…...

Knife4j系列--使用方法
原文网址:Knife4j系列--使用/教程/实例/配置_IT利刃出鞘的博客-CSDN博客...

pmp项目管理考试是什么?适合哪些人学?
PMP,简单点说,就是美国PMI为考察项目管理人士的专业能力而设立的考试。 该流程以知识和任务驱动型指南评估从业者的能力,同时确定项目经理能力行业标准,包括各项知识、任务和技能的特点、重要性与运用频率。(考纲原文…...
CSDN博客可以添加联系方式了
csdn博客一直不允许留一些联系方式,结果是官方有联系方式路径 在首页,往下拉,左侧就有 点击这个即可添加好友了~ 美滋滋,一起交流, 学习技术 ~...
小程序隐私弹窗的实现
小程序的开发者对于微信官方来说是有爱有恨,三天二头整事是鹅厂的一贯风格。 隐私弹窗的几个要点 回归正题,小程序隐私弹窗的几个要点: 1、何时弹出用户隐私协议的弹窗? 2、是每次进小程序都弹出来吗? 这两个想明…...
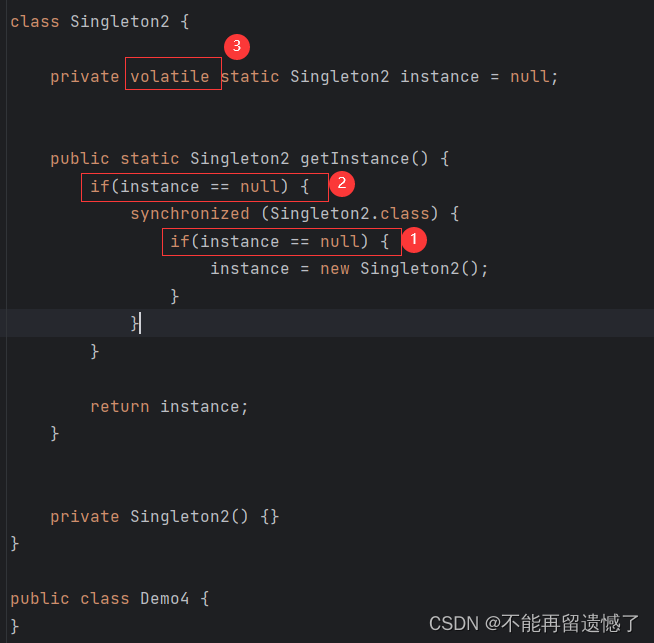
【JavaEE】多线程案例-单例模式
文章目录 1. 前言2. 什么是单例模式3. 如何实现单例模式3.1 饿汉模式3.2 懒汉模式4. 解决单例模式中遇到的线程安全问题4.1 加锁4.2 加上一个判断解决频繁加锁问题4.2 解决因指令重排序造成的线程不安全问题 1. 前言 单例模式是我们面试中最常考到的设计模式。什么是设计模式呢…...

社区分享|MeterSphere变身“啄木鸟”,助力云帐房落地接口自动化测试
云帐房网络科技有限公司(以下简称为“云帐房”)成立于2015年3月,以“成为最值得信赖的税务智能公司”为愿景,运用人工智能、大数据等互联网技术,结合深厚的财税行业服务经验,为代账公司和中大型企业提供智能…...
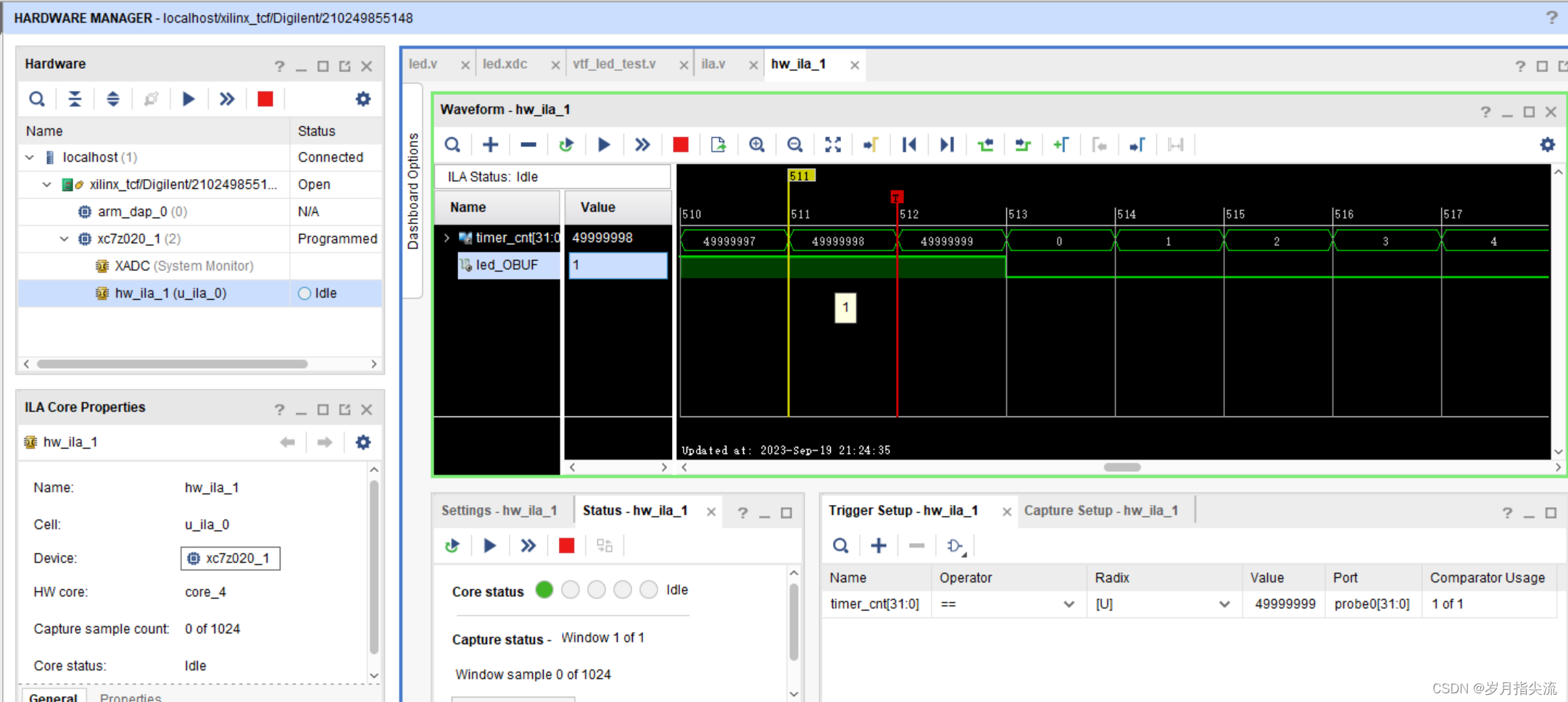
fpga内嵌逻辑分析仪使用方法
文章目录 前言一、方法1 — 使用 IP 核创建 ILA 调试环境1、创建 ILA ip 核2、进行例化3、生成比特流文件4、下载程序5、进行在线调试 二、方法2 — 使用 Debug 标记创建 ILA1、Debug 标记相关信号2、综合操作3、设置 Set Up Debug4、生成比特文件5、下载程序6、进行在线调试 前…...

第14章 结构和其他数据形式
本章介绍以下内容: 关键字:struct、union、typedef 运算符:.、-> 什么是C结构,如何创建结构模板和结构变量 如何访问结构的成员,如何编写处理结构的函数 联合和指向函数的指针 设计程序时,最重要的步骤之…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
