numpy的多项式函数: `poly1d`
Python numpy.poly1d()
numpy.poly1d()函数有助于定义一个多项式函数。它使得在多项式上应用 "自然操作 "变得容易。
语法: numpy.poly1d (arr, root, var)
参数 :
-
arr : [array_like] 多项式系数按照幂的递减顺序给出。如果第二个参数(根)被设置为True,那么数组值就是多项式方程的根。
-
root : [bool, optional] 真意味着多项式的根。默认为假
-
var : 我们在多项式中需要的变量如x、y、z。默认为x
参数:
- coefficients( coef, c) : 多项式系数
- order(o): 多项式的阶数或程度
- roots ( r): 多项式的根
返回: 多项式和应用的操作
代码1:解释poly1d()和它的参数
# Python code explaining
# numpy.poly1d()import numpy as np
p1 = np.poly1d([1, 2])
p2 = np.poly1d([4, 9, 5, 4])
print ('构建多项式:')
print ("P1 : "p1)
print ("\n p2 : \n", p2)
# 求解多项式
print (f"\n\n当x=2时, {p1(2)=}")
print (f"\n\n当x=2时, {p2(2)=}")
# 寻根
print (f"\n\nP1的根 : {p1.r=}") #Q: p1.r=[-2]? 为什么是-2? #A: 因为p1(x)=x+2, 所以p1(x)=0时, x=-2
print (f"P2的根 : {p2.roots=}")# 求系数
print (f"\n\nP1的系数 : , {p1.c=}")
print (f"P2的系数 : , {p2.coeffs=}")# Finding Order
print (f"\n\nOrder / Degree of P1的阶数 : , {p1.o=}")
print (f"Order / Degree of P2的阶数 : , {p2.order=}")
输出:
构建多项式:
P1 :
1 x + 2p2 : 3 2
4 x + 9 x + 5 x + 4当x=2时, p1(2)=4当x=2时, p2(2)=82P1的根 : p1.r=array([-2.])
P2的根 : p2.roots=array([-1.86738371+0.j , -0.19130814+0.70633545j,-0.19130814-0.70633545j])P1的系数 : p1.c=array([1, 2])
P2的系数 : p2.coeffs=array([4, 9, 5, 4])Order / Degree of P1的阶数 : p1.o=1
Order / Degree of P2的阶数 : p2.order=3
代码2:多项式的基本数学运算
p1 = np.poly1d([1, 2])
p2 = np.poly1d([4, 9, 5, 4])print ("P1 : ", p1)
print ("\n p2 : \n", p2)print ("\n\np1 ^ 2 : \n", p1**2)
print ("p2 ^ 2 : \n", np.square(p2))p3 = np.poly1d([1, 2], variable = 'y')
print ("\n\np3 : ", p3)print ("\n\np1 * p2 : \n", p1 * p2)
print ("\n多项式相乘 : \n",np.poly1d([1, -1]) * np.poly1d([1, -2]))
输出
P1 :
1 x + 2p2 : 3 2
4 x + 9 x + 5 x + 4p1 ^ 2 : 2
1 x + 4 x + 4
p2 ^ 2 : [16 81 25 16]p3 :
1 y + 2p1 * p2 : 4 3 2
4 x + 17 x + 23 x + 14 x + 8多项式相乘 : 2
1 x - 3 x + 2
以上
相关文章:

numpy的多项式函数: `poly1d`
Python numpy.poly1d() numpy.poly1d()函数有助于定义一个多项式函数。它使得在多项式上应用 "自然操作 "变得容易。 语法: numpy.poly1d (arr, root, var) 参数 : arr : [array_like] 多项式系数按照幂的递减顺序给出。如果第二个参数(根)被…...
Python灰帽编程——错误异常处理和面向对象
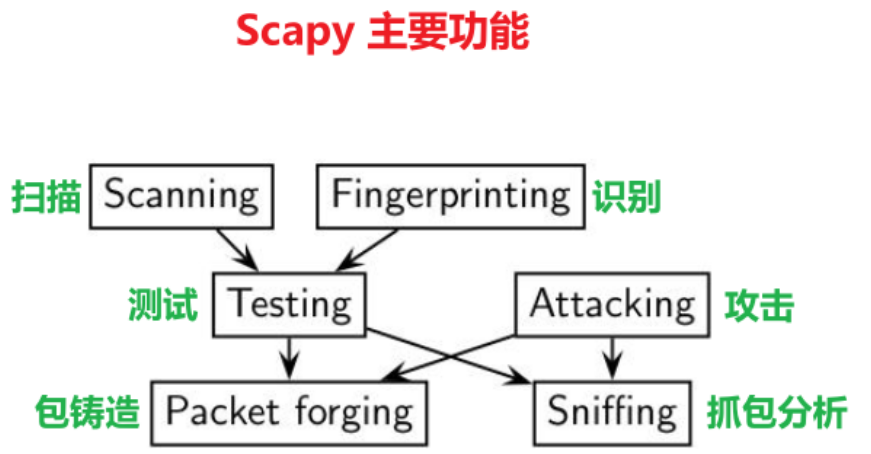
文章目录 1. 错误和异常1.1 基本概念1.1.1 Python 异常 1.2 检测(捕获)异常1.2.1 try except 语句1.2.2 捕获多种异常1.2.3 捕获所有异常 1.3 处理异常1.4 特殊场景1.4.1 with 语句 2. 内网主机存活检测程序2.1 scapy 模块2.1.1 主要功能2.1.2 scapy 安装…...
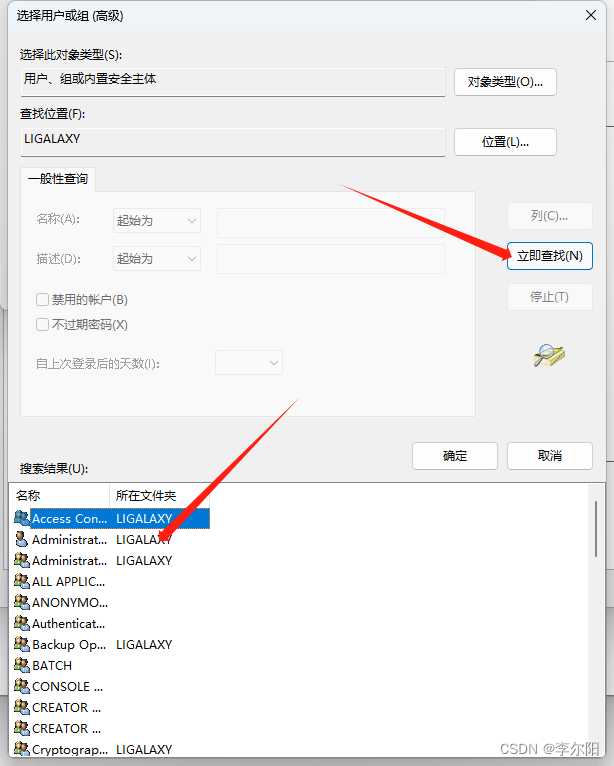
【20230919】win11无法删除Chrome注册表项
win11无法删除Chrome注册表项 删除以下注册表项发生错误: 计算机\HKEY_LOCAL_MACHINE\SOFTWAR\Google计算机\HKEY_CURRENT_USER\Software\Google 尝试了很多删除注册表方法(例如:编辑remove.reg文件),都不行。 无法…...
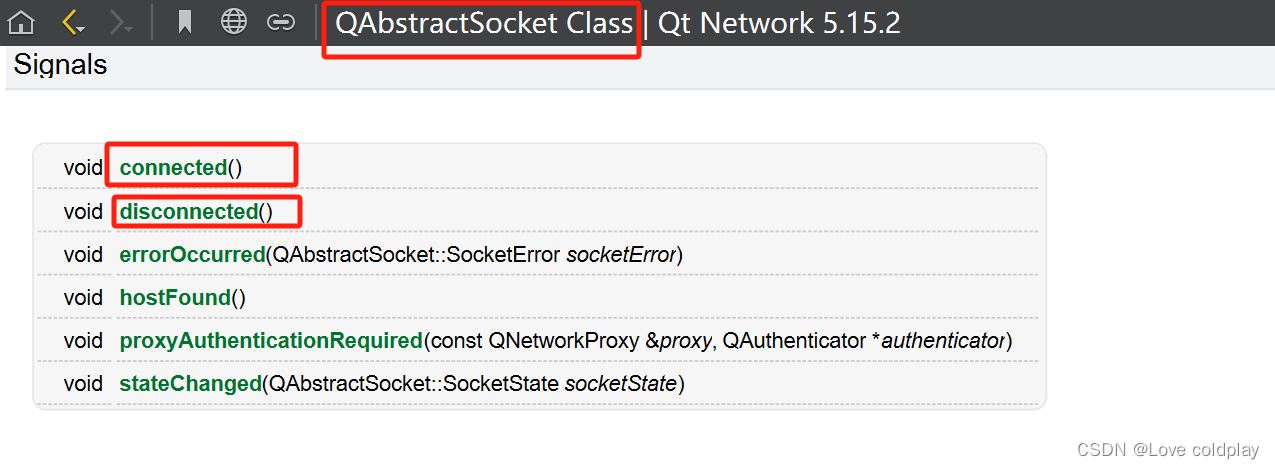
TCP/IP客户端和服务器端建立通信过程
客户端和服务器端建立通信过程 使用Qt提供的类进行基于TCP的套接字通信需要用到两个类: QTcpServer:服务器类,用于监听客户端连接以及和客户端建立连接。 QTcpSocket:通信的套接字类,客户端、服务器端都需要使用。服务…...
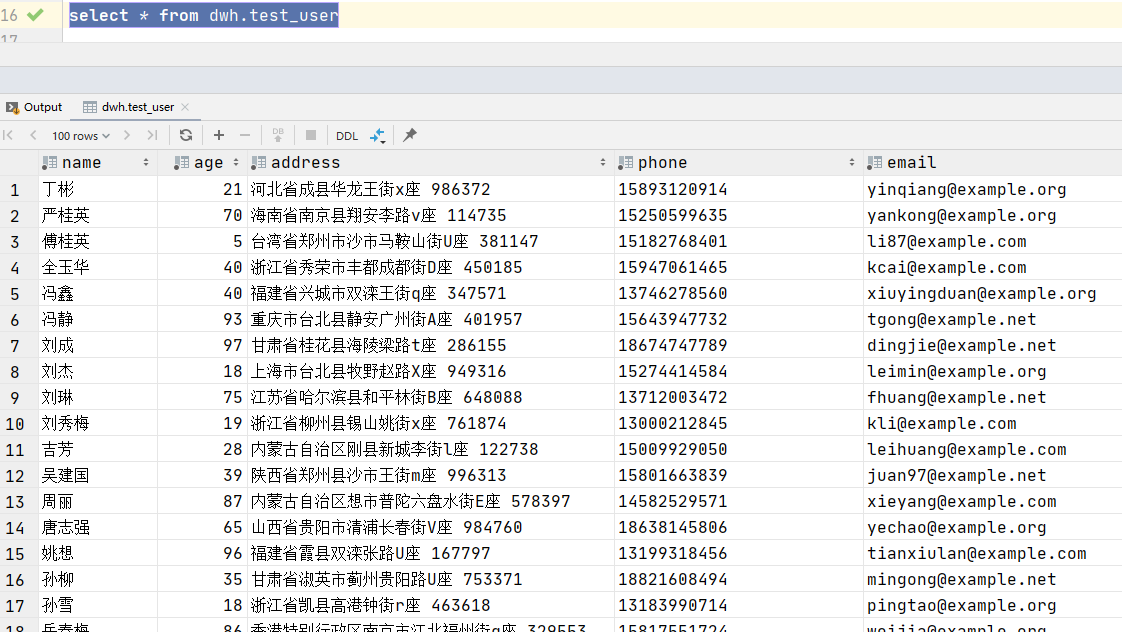
Python ---使用Fake库向clickhouse造数据小案例
每次insert太麻烦了 先在clickhosue中建表 test_user表 CREATE TABLE dwh.test_user (name String,age Int32,address String,phone String,email String ) ENGINE MergeTree() ORDER BY name; 此时表中暂无数据 用Python脚本来造一些数据 from faker import Faker from c…...

09MyBatisX插件
MyBatisX插件 在真正开发过程中对于一些复杂的SQL和多表联查就需要我们自己去编写代码和SQL语句,这个时候可以使用MyBatisX插件帮助我们简化开发 安装MyBatisX插件: File -> Settings -> Plugins -> 搜索MyBatisx插件搜索安装然后重启IDEA 跳转文件功能 由于一个项…...

使用 Messenger 跨进程通信
什么是Messenger Messenger 也是IPC的方案之一,是基于消息的跨进程通信。基于消息是什么意思?Handler是我们最常用的消息机制,所以 Messenger 对于使用者来说就像是使用 Handler。实际上 Messenger 就是 AIDL 的上层封装而已,它们…...

Spring Cloud Gateway
路由谓词工厂 Route Predicate Factory 1. The After Route Predicate Factory spring:cloud:gateway:routes:- id: after_routeuri: https://example.orgpredicates:- After2017-01-20T17:42:47.789-07:00[America/Denver]# 用日期时间匹配 2. The Before Route Pr…...

JVM 优化技术
文章目录 JVM 优化技术概述方法内联优化说明优点内联条件 栈帧之间数据共享说明优点栈帧之间数据共享条件 JVM 优化技术 概述 JVM常见的优化技术: 方法内联优化。栈帧之间数据共享。 方法内联优化 说明 方法内联(Method Inlining)是JVM…...

【MySQL系列】- MySQL自动备份详解
【MySQL系列】- MySQL自动备份详解 文章目录 【MySQL系列】- MySQL自动备份详解一、需求背景二、Windows mysql自动备份方法2.1 复制date文件夹备份实验备份环境创建bat直接备份脚本 2 .2 mysqldump备份成sql文件创建mysqldump备份脚本 2 .3 利用WinRAR对MySQL数据库进行定时备…...

指针笔试题讲解-----让指针简单易懂(2)
目录 回顾上篇重点 : 一.笔试题 ( 1 ) 二.笔试题 ( 2 ) 科普进制知识点 (1) 二进制 (2) 八进制 (3)十六进制 三.笔试题( 3 ) 四.笔试题( 4 ) 五.笔试题( 5 ) 六.笔试题( …...

使用windbg分析dump文件的方法
https://zhuanlan.zhihu.com/p/613434365 一般操作如下: 准备工作。 打开dump文件。指定符号表文件的路径。指定可执行文件的路径。指定源码文件的路径。在windbg的命令行,输入并执行如下命令 .reload,重新加载前述数据文件。!analyze -v&a…...

【论文阅读 07】Anomaly region detection and localization in metal surface inspection
比较老的一篇论文,金属表面检测中的异常区域检测与定位 总结:提出了一个找模板图的方法,使用SIFT做特征提取,姿态估计看差异有哪些,Hough聚类做描述符筛选,仿射变换可视化匹配图之间的关系…...
SSM - Springboot - MyBatis-Plus 全栈体系(十一)
第二章 SpringFramework 五、Spring AOP 面向切面编程 6. Spring AOP 基于 XML 方式实现(了解) 6.1 准备工作 加入依赖和基于注解的 AOP 时一样。准备代码把测试基于注解功能时的 Java 类复制到新 module 中,去除所有注解。 6.2 配置 Sp…...

深度剖析贪心算法:原理、优势与实战
概述 贪心算法是一种通过每一步的局部最优选择来寻找整体最优解的方法。在每个步骤中,贪心算法选择当前状态下的最佳选项,而不考虑未来可能的影响。尽管它不能保证一定能找到全局最优解,但贪心算法通常简单且高效,适用于许多实际…...

Docker搭建DNS服务器--use
前言 DNS服务器是(Domain Name System或者Domain Name Service)域名系统或者域名服务,域名系统为Internet上的主机分配域名地址和IP地址。 安装 2.1 实验环境 IP 系统版本 角色 192.168.40.121 Ubuntu 22.10 DNS服务器 192.168.40.122 Ubuntu 22.10 测试机器 2.2 …...

“顽固”——C语言用栈实现队列
解题图解: 1、 先用stack1存储push来的数据 2、每当要pop数据时,从stack2中取,如果 stack2为空,就先从stack1中“倒”数据到stack2。 这就是用栈实现队列的基本操作 这道题看起来比较容易,但是!如果你用C语…...
linux内网渗透
一、信息收集 主机发现: nmap -sP 192.168.16.0/24 端口探测 masscan -p 1-65535 192.168.16.168 --rate1000 开放端口如下 nmap端口详细信息获取 nmap -sC -p 8888,3306,888,21,80 -A 192.168.16.168 -oA ddd4-port目录扫描 gobuster dir…...

还没用熟 TypeScript 社区已经开始抛弃了
根据 rich-harris-talks-sveltekit-and-whats-next-for-svelte 这篇文章的报道, Svelte 计划要把代码从 TS 换到 JS 了。 The team is switching the underlying code from TypeScript to JavaScript. That and the update will then allow the team to incorporate…...
2023年9月19日
2> 完成文本编辑器的保存工作 头文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QFontDialog> #include <QMainWindow> #include <QFont> #include <QMessageBox> #include <QDebug> #include <QColorDialog> #include &l…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
