深度剖析贪心算法:原理、优势与实战
概述
贪心算法是一种通过每一步的局部最优选择来寻找整体最优解的方法。在每个步骤中,贪心算法选择当前状态下的最佳选项,而不考虑未来可能的影响。尽管它不能保证一定能找到全局最优解,但贪心算法通常简单且高效,适用于许多实际问题。
核心原理
贪心算法是一种寻找全局最优解的方法,其核心原理可概括为以下步骤:
-
问题建模:将问题分解成一系列子问题,每个子问题都有一定的优先级。
-
选择策略:在每个步骤中,选择当前子问题的最佳选项,即局部最优解,而不考虑未来可能的影响。
-
更新状态:根据所选策略,更新问题的状态以反映已经做出的选择。
-
重复:反复执行步骤2和步骤3,直到达到问题的终止条件。
优势
贪心算法具有以下优势:
- 高效性:贪心算法通常具有较低的时间复杂度,适用于大规模问题。
- 简单性:相对于某些复杂的动态规划算法,贪心算法的实现相对简单。
- 实用性:贪心算法适用于许多实际问题,特别是那些具有贪心选择性质的问题。
实际应用
以下是四个经典问题,以及它们的贪心算法解决方案的示例:
1. 零钱兑换问题
问题描述:给定不同面额的硬币 coins 和一个总金额 amount,编写一个函数来计算可以凑成总金额所需的最少的硬币个数。
Python 示例
def coinChange(coins, amount):coins.sort(reverse=True)count = 0for coin in coins:while amount >= coin:amount -= coincount += 1return count if amount == 0 else -1
Java 示例
public int coinChange(int[] coins, int amount) {Arrays.sort(coins);int count = 0;for (int i = coins.length - 1; i >= 0; i--) {while (amount >= coins[i]) {amount -= coins[i];count++;}}return amount == 0 ? count : -1;
}
2. 背包问题
问题描述:给定一组物品,每个物品都有自己的重量和价值,以及一个容量限制的背包。目标是找到将哪些物品放入背包,可以使得背包中的物品总价值最大。
Python 示例:
def knapsack(values, weights, capacity):n = len(values)items = [(values[i], weights[i]) for i in range(n)]items.sort(key=lambda x: x[1] / x[0], reverse=True)total_value = 0for item in items:if capacity >= item[1]:total_value += item[0]capacity -= item[1]return total_value
Java 示例
public int knapsack(int[] values, int[] weights, int capacity) {int n = values.length;Item[] items = new Item[n];for (int i = 0; i < n; i++) {items[i] = new Item(values[i], weights[i]);}Arrays.sort(items, (a, b) -> Double.compare(b.valuePerWeight, a.valuePerWeight));int totalValue = 0;for (Item item : items) {if (capacity >= item.weight) {totalValue += item.value;capacity -= item.weight;}}return totalValue;
}class Item {int value;int weight;double valuePerWeight;Item(int value, int weight) {this.value = value;this.weight = weight;valuePerWeight = (double) value / weight;}
}
3.最小生成树问题
问题描述:给定一个连通的带权无向图,目标是找到一棵生成树,使得其包含所有顶点并且总权值最小。
Python 示例
class Graph:def __init__(self, vertices):self.V = verticesself.graph = []def add_edge(self, u, v, w):self.graph.append([u, v, w])def kruskal_mst(self):result = []self.graph = sorted(self.graph, key=lambda item: item[2])parent = []rank = []def find(i):if parent[i] == i:return ireturn find(parent[i])def union(i, j):i_root = find(i)j_root = find(j)if i_root != j_root:if rank[i_root] < rank[j_root]:parent[i_root] = j_rootelif rank[i_root] > rank[j_root]:parent[j_root] = i_rootelse:parent[j_root] = i_rootrank[i_root] += 1for node in range(self.V):parent.append(node)rank.append(0)i = 0e = 0while e < self.V - 1:u, v, w = self.graph[i]i += 1x = find(u)y = find(v)if x != y:e += 1result.append([u, v, w])union(x, y)minimum_cost = 0for u, v, weight in result:minimum_cost += weightprint(f"Edge ({u}-{v}) Weight: {weight}")print(f"Minimum Spanning Tree Weight: {minimum_cost}")# 创建一个带权无向图
g = Graph(4)
g.add_edge(0, 1, 10)
g.add_edge(0, 2, 6)
g.add_edge(0, 3, 5)
g.add_edge(1, 3, 15)
g.add_edge(2, 3, 4)# 执行Kruskal算法找到最小生成树
g.kruskal_mst()
Java 示例
import java.util.*;class Graph {private int V, E;private List<Edge> edges;static class Edge {int src, dest, weight;Edge(int src, int dest, int weight) {this.src = src;this.dest = dest;this.weight = weight;}}Graph(int V, int E) {this.V = V;this.E = E;edges = new ArrayList<>();}void addEdge(int src, int dest, int weight) {edges.add(new Edge(src, dest, weight));}int kruskalMST() {int result = 0;edges.sort(Comparator.comparingInt(e -> e.weight));int[] parent = new int[V];Arrays.fill(parent, -1);int edgeCount = 0;for (Edge edge : edges) {int srcParent = find(parent, edge.src);int destParent = find(parent, edge.dest);if (srcParent != destParent) {result += edge.weight;parent[srcParent] = destParent;edgeCount++;}if (edgeCount == V - 1) break;}return result;}private int find(int[] parent, int node) {if (parent[node] == -1) return node;return find(parent, parent[node]);}
}public class MinimumSpanningTree {public static void main(String[] args) {Graph graph = new Graph(4, 5);graph.addEdge(0, 1, 10);graph.addEdge(0, 2, 6);graph.addEdge(0, 3, 5);graph.addEdge(1, 3, 15);graph.addEdge(2, 3, 4);int minWeight = graph.kruskalMST();System.out.println("Minimum Spanning Tree Weight: " + minWeight);}
}4.Huffman编码
问题描述:给定一组字符及其出现频率,目标是构建一种前缀编码,使得出现频率高的字符具有较短的编码。
Python 示例
import heapq
from collections import defaultdictclass HuffmanNode:def __init__(self, char, freq):self.char = charself.freq = freqself.left = Noneself.right = Nonedef __lt__(self, other):return self.freq < other.freqdef build_huffman_tree(chars, freq):heap = [HuffmanNode(char, freq) for char, freq in zip(chars, freq)]heapq.heapify(heap)while len(heap) > 1:left = heapq.heappop(heap)right = heapq.heappop(heap)merged = HuffmanNode('$', left.freq + right.freq)merged.left = leftmerged.right = rightheapq.heappush(heap, merged)return heap[0]def print_huffman_codes(node, code=""):if node is None:returnif node.char != '$':print(f"Character: {node.char}, Code: {code}")print_huffman_codes(node.left, code + "0")print_huffman_codes(node.right, code + "1")# 给定字符和频率数据
chars = ['a', 'b', 'c', 'd', 'e', 'f']
freq = [5, 9, 12, 13, 16, 45]# 构建Huffman编码树
root = build_huffman_tree(chars, freq)# 打印Huffman编码
print_huffman_codes(root)
Java 示例
import java.util.*;class HuffmanNode {char data;int frequency;HuffmanNode left, right;HuffmanNode(char data, int frequency) {this.data = data;this.frequency = frequency;left = right = null;}
}public class HuffmanCoding {public static void main(String[] args) {char[] chars = {'a', 'b', 'c', 'd', 'e', 'f'};int[] freq = {5, 9, 12, 13, 16, 45};HuffmanNode root = buildHuffmanTree(chars, freq);printHuffmanCodes(root, "");}public static HuffmanNode buildHuffmanTree(char[] chars, int[] freq) {PriorityQueue<HuffmanNode> queue = new PriorityQueue<>(Comparator.comparingInt(node -> node.frequency));for (int i = 0; i < chars.length; i++) {queue.add(new HuffmanNode(chars[i], freq[i]));}while (queue.size() > 1) {HuffmanNode left = queue.poll();HuffmanNode right = queue.poll();HuffmanNode newNode = new HuffmanNode('$', left.frequency + right.frequency);newNode.left = left;newNode.right = right;queue.add(newNode);}return queue.poll();}public static void printHuffmanCodes(HuffmanNode node, String code) {if (node == null) {return;}if (node.data != '$') {System.out.println("Character: " + node.data + ", Code: " + code);}printHuffmanCodes(node.left, code + "0");printHuffmanCodes(node.right, code + "1");}
}
相关文章:

深度剖析贪心算法:原理、优势与实战
概述 贪心算法是一种通过每一步的局部最优选择来寻找整体最优解的方法。在每个步骤中,贪心算法选择当前状态下的最佳选项,而不考虑未来可能的影响。尽管它不能保证一定能找到全局最优解,但贪心算法通常简单且高效,适用于许多实际…...

Docker搭建DNS服务器--use
前言 DNS服务器是(Domain Name System或者Domain Name Service)域名系统或者域名服务,域名系统为Internet上的主机分配域名地址和IP地址。 安装 2.1 实验环境 IP 系统版本 角色 192.168.40.121 Ubuntu 22.10 DNS服务器 192.168.40.122 Ubuntu 22.10 测试机器 2.2 …...

“顽固”——C语言用栈实现队列
解题图解: 1、 先用stack1存储push来的数据 2、每当要pop数据时,从stack2中取,如果 stack2为空,就先从stack1中“倒”数据到stack2。 这就是用栈实现队列的基本操作 这道题看起来比较容易,但是!如果你用C语…...
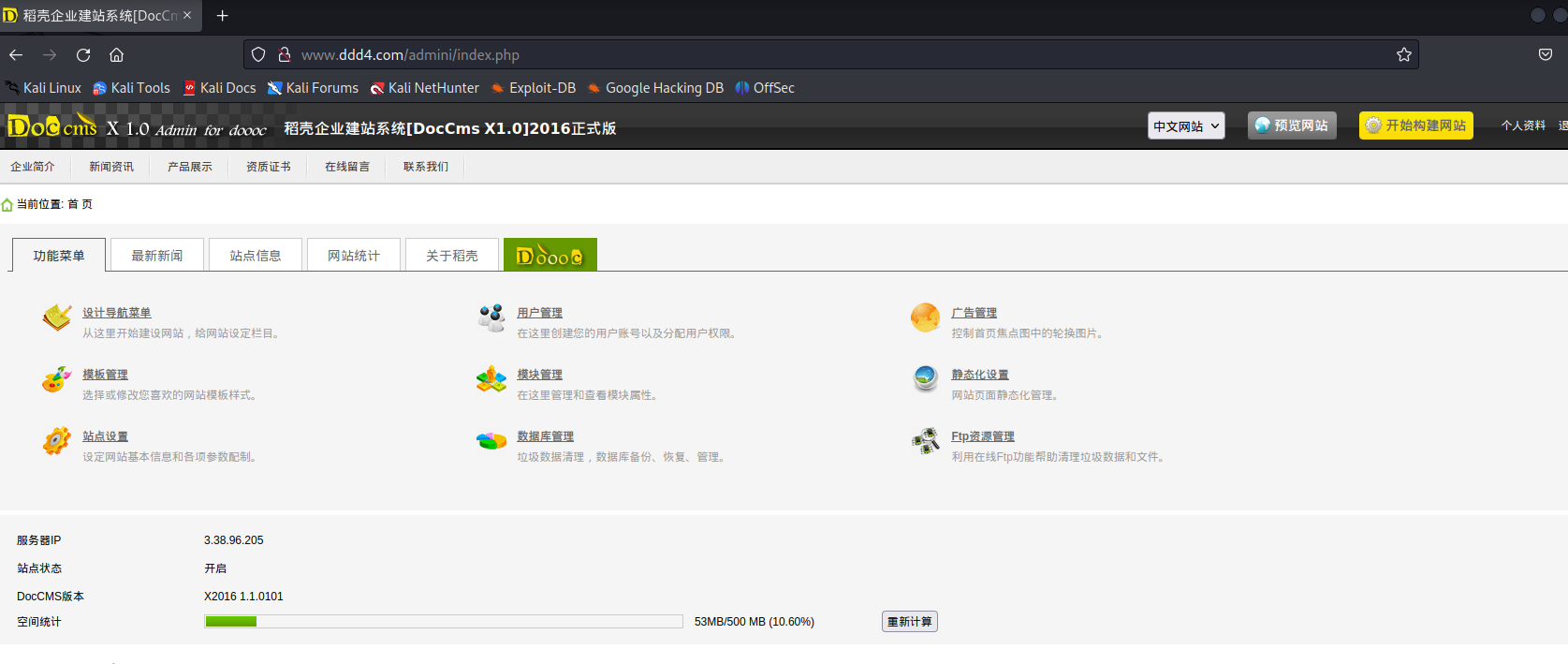
linux内网渗透
一、信息收集 主机发现: nmap -sP 192.168.16.0/24 端口探测 masscan -p 1-65535 192.168.16.168 --rate1000 开放端口如下 nmap端口详细信息获取 nmap -sC -p 8888,3306,888,21,80 -A 192.168.16.168 -oA ddd4-port目录扫描 gobuster dir…...

还没用熟 TypeScript 社区已经开始抛弃了
根据 rich-harris-talks-sveltekit-and-whats-next-for-svelte 这篇文章的报道, Svelte 计划要把代码从 TS 换到 JS 了。 The team is switching the underlying code from TypeScript to JavaScript. That and the update will then allow the team to incorporate…...
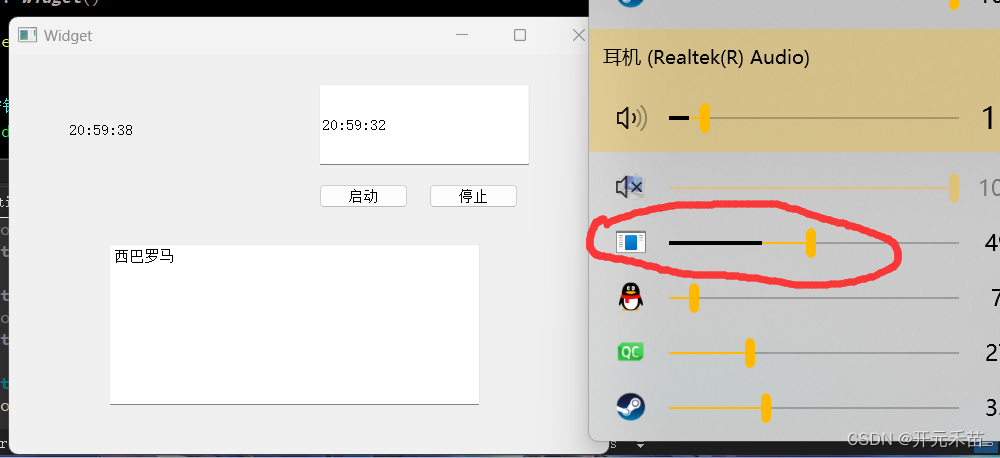
2023年9月19日
2> 完成文本编辑器的保存工作 头文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QFontDialog> #include <QMainWindow> #include <QFont> #include <QMessageBox> #include <QDebug> #include <QColorDialog> #include &l…...
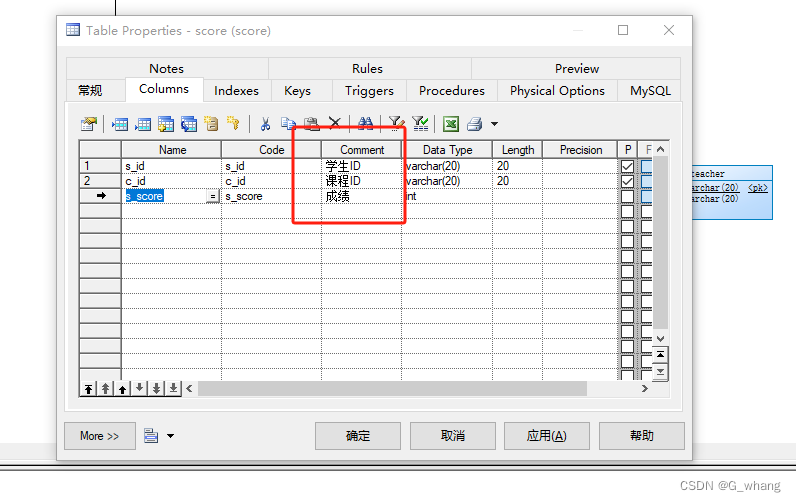
PowerDesigner 与 mysql 同步数据
PowerDesigner 连接上数据库 创建数据库表 table_5 选择: 点击确认后弹出 点击run执行 刷新数据库表,已创建成功 修改测试表1,新增一个字段 取消全选 选择数据库,勾选修改的表,如果全部勾选的话,就…...

[python 刷题] 271 Encode and Decode Strings
[python 刷题] 271 Encode and Decode Strings 题目: Design an algorithm to encode a list of strings to a string. The encoded string is then sent over the network and is decoded back to the original list of strings. Machine 1 (sender) has the func…...

[QT]day3
1.一个闹钟 widget.cpp: #include "widget.h" #include "ui_widget.h"#include <QWidget> #include <QTimerEvent> //定时器事件处理类 #include <QTime>Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {//给播…...

《PostgreSQL事务管理深入解析》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

深度分析Oracle中的NULL
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 关键点 特殊值NULL意味着没有数据,它声明了该值是未知的事实。默认情况下,任何类型的列和变量都可以取这个值,除非它们有一个NOT N…...

Python入门教学——类和对象
目录 一、面向过程和面向对象 1、面向过程 2、面向对象 二、类 三、类对象与类属性 1、类对象 2、类属性 四、类方法与静态方法 1、类方法 2、静态方法 一、面向过程和面向对象 1、面向过程 是一种以过程为中心的编程思想,强调事件的流程和顺序。思想&…...
【数据库系统概论】关系数据库中的关系数据结构
前言关系关系模式关系数据库关系模型的存储结构感谢 💖 前言 上一篇文章【数据库系统概论】数据模型介绍了数据库系统中的数据模型的基本概念。其中提到了关系模型是最重要的一种数据模型。下面将介绍支持关系模型的数据库系统——关系数据库。 按照数据模型的三大…...
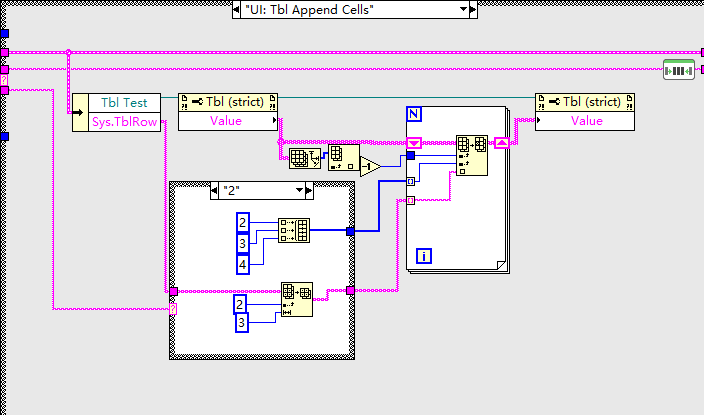
LabVIEW对Table中同一行数据分多次增加
LabVIEW对Table中同一行数据分多次增加 在对多个设备采集数据,同时需要记录到表格中。很多时候多台数据并不是同时更新,比如有的是在开关之前读取更新,有的则是在开关闭合后更新。只是用Number Indicator的方式,需要很多个&#…...

微信小程序实现删除功能
1. 前端 项目列表展示是使用的wx:for遍历 每个项目展示有3个模块 1. project-title 2. project-content 3. project-foot 全部代码如下 <t-sticky><view class"search"><t-search model:value"{{conditions.keyword}}" pl…...

整合Shiro+Jwt
整合ShiroJwt大体思路 springboot整合shiro大体上的思路: 1.自定义一个类Realm extends AuthorizingRealm{} 主要是对token授权和认证 重写2个方法 doGetAuthorizationInfo //授权 doGetAuthenticationInfo //认证 认证 代码中手动加上对token校验的判断2.自…...
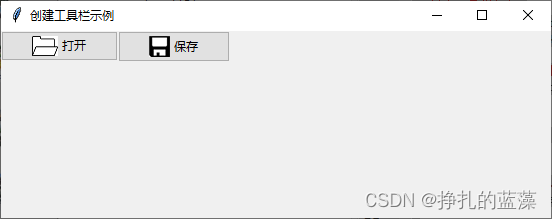
Python 图形化界面基础篇:创建工具栏
Python 图形化界面基础篇:创建工具栏 引言 Tkinter 库简介步骤1:导入 Tkinter 模块步骤2:创建 Tkinter 窗口步骤3:创建工具栏步骤4:向工具栏添加工具按钮步骤5:处理工具按钮的点击事件步骤6:启动…...
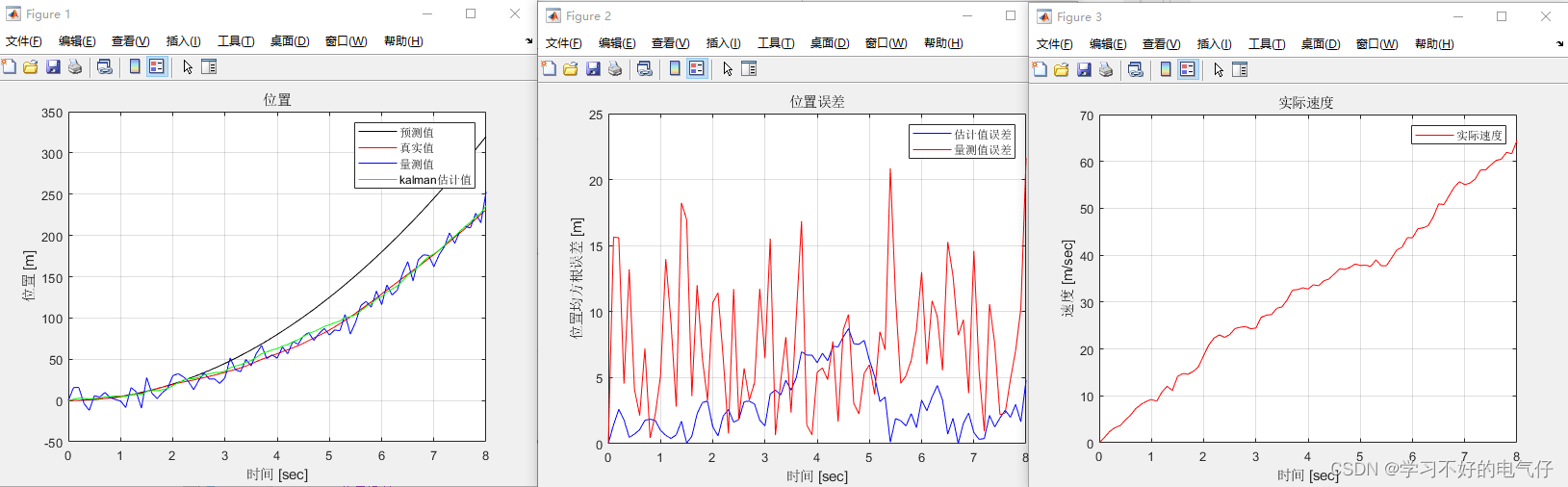
基于matlab实现的卡尔曼滤波匀加速直线运动仿真
完整程序: clear clc %% 初始化参数 delta_t 0.1; %采样时间 T 8; %总运行时长 t 0:delta_t:T; %时间序列 N length(t); %序列的长度 x0 0; %初始位置 u0 0; %初速度 U 10; %控制量、加速度 F [1 delta_t 0 1]; %状态转移矩阵 B …...
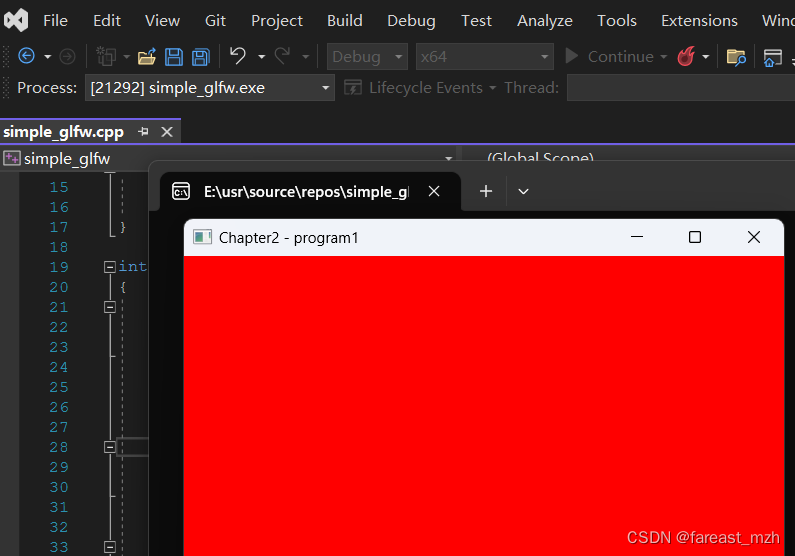
windows Visual Studio 2022 opengl开发环境配置
1. 安装glew(GL), GLFW, glm, soil2-debug 还需要premake生成visual studio solution cmake for windows也要安装一个, 但是不用安装MinGW64, bug多 下载源码,找到xxx.sln文件用visual stidio打开solution编译代码,找到xxx.lib, xxx.dll文件…...

中国财政科学研究院党委书记、院长刘尚希一行莅临麒麟信安调研
为贯彻落实省委第十二届四次全会精神,加快推动湖南高质量发展,9月16日下午,由中国财政科学研究院党委书记、院长刘尚希,中国电子信息产业发展研究院总工程师秦海林,省委改革办副主任梁仲,省发展改革委党组成…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
