深入解析Perlin Simplex噪声函数:在C++中构建现代、高效、免费的3D图形背景
引言
在计算机图形中,噪声是一个经常被讨论的话题。无论是为了制造自然的纹理,还是为了模拟复杂的现实世界现象,噪声函数都在其中起着关键作用。而在众多噪声函数中,Perlin Simplex 噪声无疑是最受欢迎的一种。其原因不仅在于其干净、快速的特性,更因为其所提供的连续性和一致性非常适合图形渲染。本文将为你展示如何在C++中实现一个Perlin Simplex噪声函数。
1. Perlin Simplex 噪声:背后的原理
1.1 什么是Perlin噪声?
Perlin噪声是由Ken Perlin在1983年为电影《Tron》开发的。它是一种渐变噪声,不同于常规的随机噪声。渐变噪声的关键特性是它的连续性,这意味着相邻的值会有某种逻辑上的联系,而不是完全随机。
1.2 Simplex vs Classic Perlin噪声
尽管原始的Perlin噪声非常成功,但Ken Perlin后来发现了一些可以改进的地方。这就是Simplex噪声的由来。与经典的Perlin噪声相比,Simplex噪声提供了更少的视觉伪影,更快的计算速度,尤其在高维度的情况下。
2. C++实现:开始之前
为了实现Perlin Simplex噪声,我们首先需要准备一些基础工具和数据结构。
2.1 导入必要的库
我们将使用C++的标准库来完成大部分的工作:
#include <cmath>
#include <vector>
#include <algorithm>
2.2 定义基础数据结构
在进一步进行之前,我们需要一个表示3D点的结构:
struct Vector3 {float x, y, z;Vector3(float x = 0.0f, float y = 0.0f, float z = 0.0f): x(x), y(y), z(z) {}
};
这样,我们就有了一个简单的3D点来表示空间中的位置。
3. 网格与渐变向量
要理解Perlin Simplex噪声,必须首先了解其背后的两个核心概念:网格和渐变向量。
3.1 网格
首先,我们假设空间被划分成了一个个的立方体。每个立方体都有一个整数坐标(i, j, k)。空间中的任何点都可以通过这三个坐标来定位。
3.2 渐变向量
为了生成噪声,我们需要为每个立方体的角分配一个随机的3D向量,这就是所谓的渐变向量。我们将使用一个预定义的数组来存储这些向量:
std::vector<Vector3> gradients;
我们会在稍后的部分为这个数组分配随机向量。
注意:为了简洁和清晰,本文中的代码可能不是最优的或最完整的实现。为了获得完整的项目和更多的优化技巧,请下载完整项目
4. 初始化渐变向量
为了生成连续的噪声,我们需要确保每个顶点上的渐变向量是一致的。为此,我们会使用一个预定义的渐变向量集,并随机地为每个顶点选择一个向量。
4.1 预定义渐变向量集
我们可以选择以下12个3D向量作为预定义的渐变向量集:
const std::vector<Vector3> predefined_gradients = {Vector3(1,1,0), Vector3(-1,1,0), Vector3(1,-1,0), Vector3(-1,-1,0),Vector3(1,0,1), Vector3(-1,0,1), Vector3(1,0,-1), Vector3(-1,0,-1),Vector3(0,1,1), Vector3(0,-1,1), Vector3(0,1,-1), Vector3(0,-1,-1)
};
4.2 为每个顶点分配渐变向量
接下来,我们需要使用一种随机化策略为每个顶点分配一个渐变向量。为了保持结果的连续性,我们使用一个hash函数来确保相同的输入总是产生相同的输出:
int hash(int x, int y, int z) {int result = x * 73856093 ^ y * 19349663 ^ z * 83492791;return result & (predefined_gradients.size() - 1);
}Vector3 getGradient(int x, int y, int z) {int hashedValue = hash(x, y, z);return predefined_gradients[hashedValue];
}
通过这种方式,我们确保每个空间的顶点都被分配了一个固定的渐变向量。
5. 计算噪声值
有了渐变向量,我们就可以开始计算Perlin Simplex噪声了。
5.1 计算权重
我们首先需要为空间中的每个点计算一个权重。权重是根据点与顶点的距离计算的:
float weight(float distance) {float t = 3.0f - 2.0f * distance;return t * t * t * (distance * distance * (6.0f * t - 15.0f) + 10.0f);
}
5.2 为每个顶点计算贡献
接下来,我们将计算空间中每个点受其相邻顶点的影响:
float computeNoiseContribution(float x, float y, float z, int gridX, int gridY, int gridZ) {Vector3 gradient = getGradient(gridX, gridY, gridZ);float distanceX = x - (float)gridX;float distanceY = y - (float)gridY;float distanceZ = z - (float)gridZ;float dotProduct = gradient.x * distanceX + gradient.y * distanceY + gradient.z * distanceZ;float weightValue = weight(sqrt(distanceX * distanceX + distanceY * distanceY + distanceZ * distanceZ));return dotProduct * weightValue;
}
这个函数返回点(x, y, z)受顶点(gridX, gridY, gridZ)的影响。
5.3 计算总噪声值
现在,我们可以为任意点计算其Perlin Simplex噪声值了:
float computePerlinNoise(float x, float y, float z) {int intX = (int)x;int intY = (int)y;int intZ = (int)z;float result = 0.0f;for (int dx = 0; dx <= 1; dx++) {for (int dy = 0; dy <= 1; dy++) {for (int dz = 0; dz <= 1; dz++) {result += computeNoiseContribution(x, y, z, intX + dx, intY + dy, intZ + dz);}}}return result;
}
以上就是计算Perlin Simplex噪声值的过程。
这是第二部分的内容,描述了如何在C++中实现Perlin Simplex噪声。在接下来的部分,我们将探讨如何优化和使用这个函数,以及它在实际应用中的可能用途。
6. 优化和调整
虽然上述实现已经能够为我们生成Perlin Simplex噪声,但在实际应用中,我们通常需要进行一些优化和调整,以适应特定的需求。
6.1 多重Octave
为了获得更丰富的噪声纹理,我们通常会使用多个频率和振幅的噪声叠加。这种方法称为多重Octave。下面是如何实现它:
float computeMultiOctavePerlinNoise(float x, float y, float z, int octaves, float persistence) {float total = 0;float frequency = 1;float amplitude = 1;float maxValue = 0;for(int i=0; i<octaves; i++) {total += computePerlinNoise(x * frequency, y * frequency, z * frequency) * amplitude;maxValue += amplitude;amplitude *= persistence;frequency *= 2;}return total / maxValue;
}
在这里,octaves决定了噪声叠加的次数,而persistence决定了每一次叠加时振幅的衰减。
6.2 无缝平铺
在某些应用中,我们可能需要无缝地平铺噪声纹理。要实现这一点,可以通过周期性地包装噪声值来实现:
float computeTiledPerlinNoise(float x, float y, float z, float tileWidth) {float tiledX = fmod(x, tileWidth) / tileWidth;float tiledY = fmod(y, tileWidth) / tileWidth;float tiledZ = fmod(z, tileWidth) / tileWidth;return computeMultiOctavePerlinNoise(tiledX, tiledY, tiledZ, 4, 0.5);
}
7. Perlin Simplex噪声的应用
Perlin Simplex噪声具有广泛的应用价值。以下是一些常见的应用场景:
7.1 地形生成
可以使用Perlin Simplex噪声来创建自然且连续的地形高度图。
7.2 纹理生成
噪声可以帮助我们创建各种各样的自然纹理,如云、水、火等。
7.3 模拟
在物理模拟中,噪声可以为流体或火焰动画添加细节和随机性。
7.4 3D建模
在3D建模中,噪声可用于产生随机的表面细节,如岩石或树皮的纹理。
结论
Perlin Simplex噪声是图形学中的一个强大工具,尤其是在需要模拟自然现象或创建复杂纹理的场合。本文为您提供了一个在C++中实现该噪声的方法,希望您能够利用这一技术为您的项目带来更多创意和实用性。
注意:为了简洁和清晰,本文中的代码可能不是最优的或最完整的实现。为了获得完整的项目和更多的优化技巧,请下载完整项目
相关文章:

深入解析Perlin Simplex噪声函数:在C++中构建现代、高效、免费的3D图形背景
引言 在计算机图形中,噪声是一个经常被讨论的话题。无论是为了制造自然的纹理,还是为了模拟复杂的现实世界现象,噪声函数都在其中起着关键作用。而在众多噪声函数中,Perlin Simplex 噪声无疑是最受欢迎的一种。其原因不仅在于其干…...

【计算机辅助蛋白质结构分析、分子对接、片段药物设计技术与应用】
第一天 上午 生物分子互作基础 1.生物分子相互作用研究方法 1.1蛋白-小分子、蛋白-蛋白相互作用原理 1.2 分子对接研究生物分子相互作用 1.3 蛋白蛋白对接研究分子相互作用 蛋白数据库 1. PDB 数据库介绍 1.1 PDB蛋白数据库功能 1.2 PDB蛋白数据可获取资源 1.3 PDB蛋白数据库对…...
免费开箱即用微鳄售后工单管理系统
编者按:本文介绍基于天翎MyApps低代码平台开发的微鳄售后工单管理系统, 引入低代码平台可以帮助企业快速搭建和部署售后工单管理系统, 以工作流作为支撑,在线完成各环节数据审批,解决售后 工单 服务的全生命周期过程管…...

vant 组件库的基本使用
文章目录 vant组件库1、什么是组件库2、vant组件 全部导入 和 按需导入的区别3、全部导入的使用步骤:4、按需导入的使用步骤:5、封装vant文件包 vant组件库 该项目将使用到vant-ui组件库,这里的目标就是认识他,铺垫知识 1、什么…...
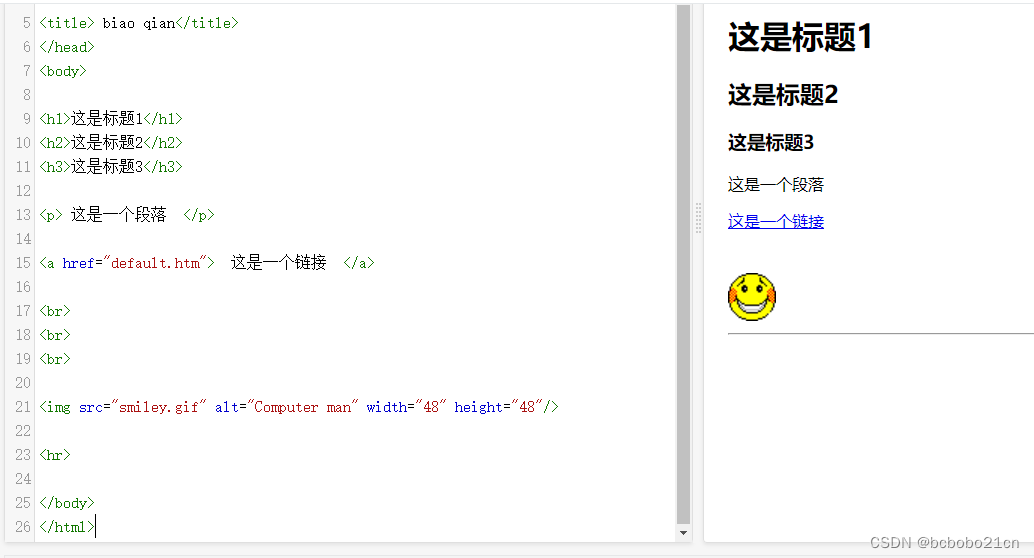
HTML常用基本元素总结
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title> biao qian</title> </head> <body><h1>这是标题1</h1> <h2>这是标题2</h2> <h3>这是标题3</h3><p> 这…...

msvcp140.dll重新安装的解决方法是什么?(最新方法)
msvcp140.dll 是 Microsoft Visual C Redistributable 的一个动态链接库文件,它包含了 C 运行时库的一些函数和类,对于许多应用程序和游戏来说都是必需的。如果您的系统中缺失了这个文件,可能会导致程序无法正常运行。下面我们将分享修复 msv…...

USI-0002 SDI-1624 HONEYWELL ,用于工业和物流4.0的人工智能
USI-0002 SDI-1624 HONEYWELL ,用于工业和物流4.0的人工智能 生产、仓库、运输——生产、储存、分拣或包装货物的地方,也是提货的地方。这意味着几个单独的货物从存储单元如箱子或纸盒中取出并重新组装。有了FLAIROP(机器人采摘的联邦学习)项目费斯托…...
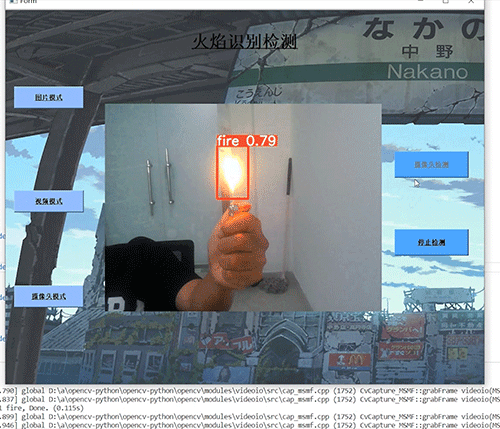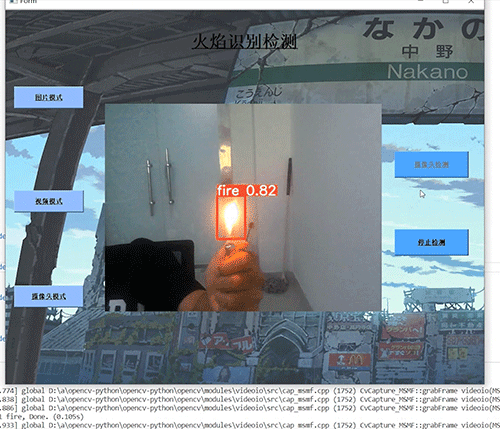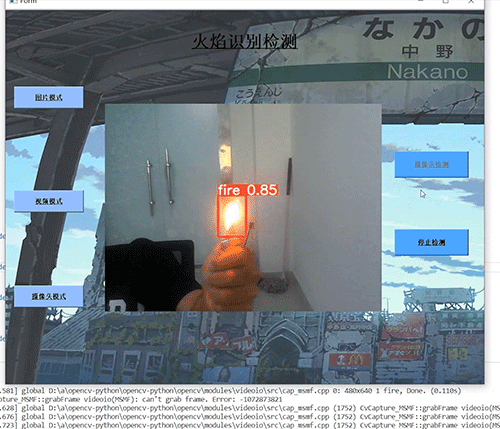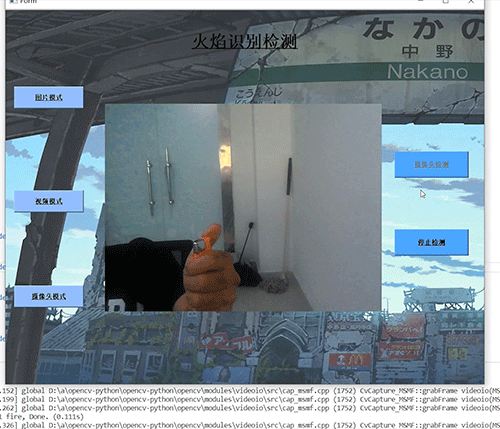
计算机竞赛 深度学习 python opencv 火焰检测识别
文章目录 0 前言1 基于YOLO的火焰检测与识别2 课题背景3 卷积神经网络3.1 卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 YOLOV54.1 网络架构图4.2 输入端4.3 基准网络4.4 Neck网络4.5 Head输出层 5 数据集准备5.1 数…...
Intellij idea 2023 年下载、安装教程、亲测可用
文章目录 1 下载与安装IDEA2 常用设置设置 Java JDK 版本自动导入包、移除包IDEA 自动生成 author 注释签名java.io.File 类无法自动提示导入?高亮显示与选中字符串相同的内容IDEA 配置 MavenIDEA 连接 Mysql 数据库 3 参考文章 1 下载与安装IDEA 首先先到官网下载…...

AI文本创作在百度App发文的实践
作者 | 内容生态端团队 导读 大语言模型(LLM)指包含数百亿(或更多)参数的语言模型,这些模型通常在大规模数据集上进行训练,以提高其性能和泛化能力。在内容创作工具接入文心一言AI能力后,可以为…...
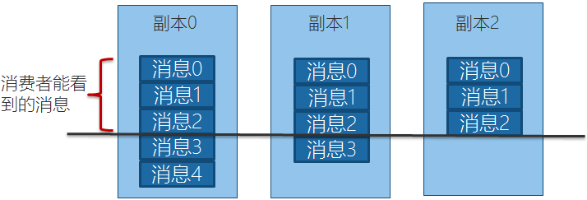
Kafka 集群与可靠性
文章目录 Kafka集群的目标Kafka集群规模如何预估Kafka集群搭建实战Kafka集群原理成员关系与控制器集群工作机制replication-factor参数auto.leader.rebalance.enable参数 集群消息生产可靠的生产者ISR(In-sync Replicas)使用ISR方案的原因ISR相关配置说明…...

【刷题】蓝桥杯
蓝桥杯2023年第十四届省赛真题-平方差 - C语言网 (dotcpp.com) 初步想法,x y2 − z2(yz)(y-z) 即xa*b,ayz,by-z 2yab 即ab是2的倍数就好了。 即x存在两个因数之和为偶数就能满足条件。 但时间是(r-l)*x&am…...

C++入门及简单例子_4
1. 类和对象: #include <iostream> // 包含输入输出流库的头文件class Rectangle { // 定义名为Rectangle的类 private: // 私有成员变量部分double length; // 长度double width; // 宽度public: // 公有成员函数部分Rectangle(double len, double w…...

成集云 | 用友U8集成聚水潭ERP(用友U8主管库存)| 解决方案
源系统成集云目标系统 方案介绍 用友U8是一套企业级的解决方案,可满足不同的制造、商务模式下,不同运营模式下的企业经营管理。它全面集成了财务、生产制造及供应链的成熟应用,并延伸客户管理至客户关系管理(CRM)&am…...
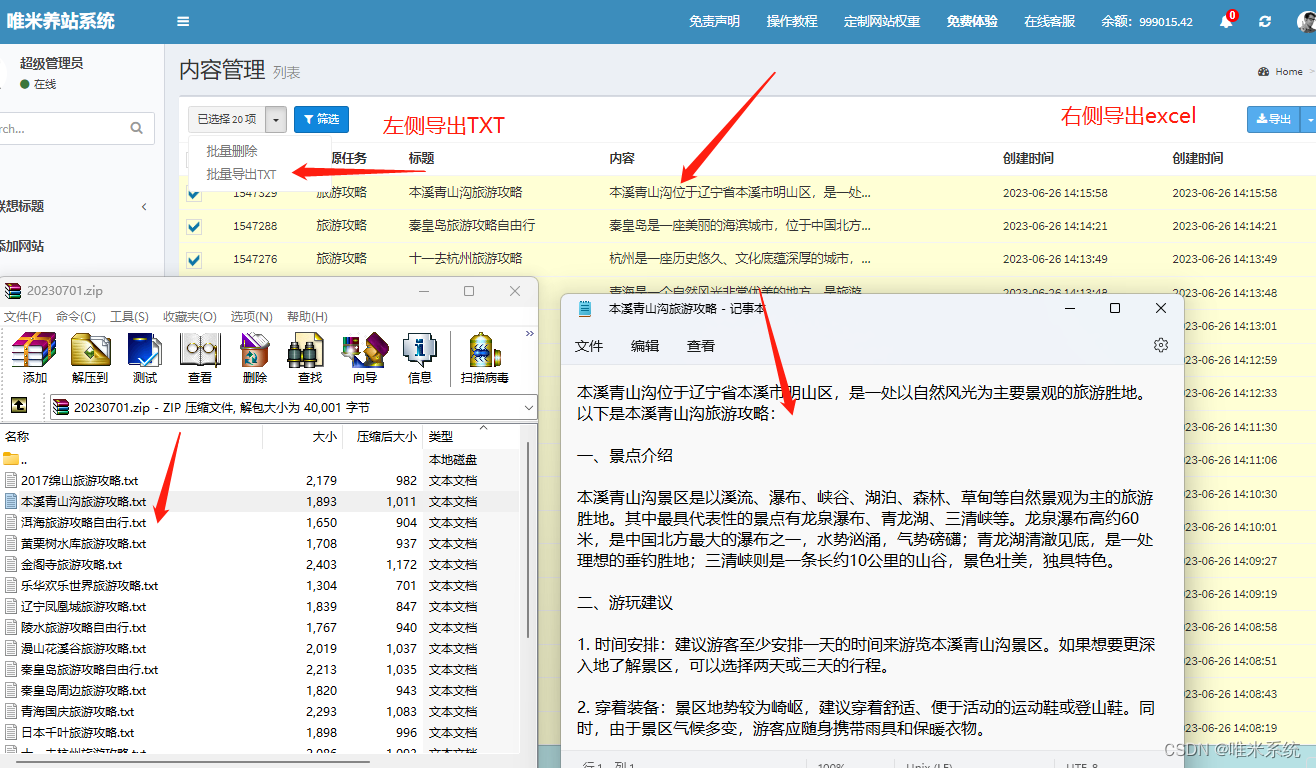
提升网站效率与SEO优化:ZBlog插件集成解决方案
在创建和管理网站的过程中,使用合适的工具和插件可以大幅提升效率,并改善搜索引擎优化(SEO)结果。ZBlog插件是为ZBlogCMS设计的一组工具,它们帮助网站管理员轻松地满足各种需求,从采集内容到发布、推送和SE…...
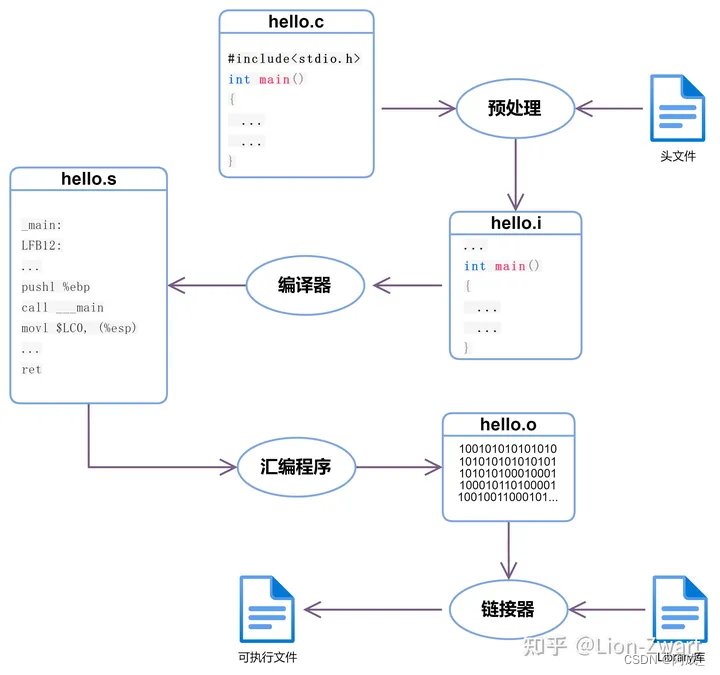
C语言的编译过程详解
当我们编译C程序时会发生什么?编译过程中的组件有哪些,编译执行过程是什么样的? 什么是编译 C语言的编译过程就是把我们可以理解的高级语言代码转换为计算机可以理解的机器代码的过程,其实就是一个翻译的过程。 …...

无人机航测没信号?北斗卫星来解决
无人机航测是利用无人机进行地理信息的采集和处理的航测方式。相比传统的航测手段,无人机航测具备更高的灵活性、更低的成本和更广阔的适应性。无人机航测可以应用于土地测绘、农业植保、城市规划、自然资源调查等多个领域,极大地提高了测绘的效率和准确…...

Vue 03 数据绑定
Vue中有2种数据绑定的方式: 1.单向绑定(v-bind): 数据只能从data流向页面。 2.双向绑定(v-model): 数据不仅能从data流向页面,还可以从页面流向data。 备注: 1.双向绑定一般都应用在表单类元素上(如&am…...
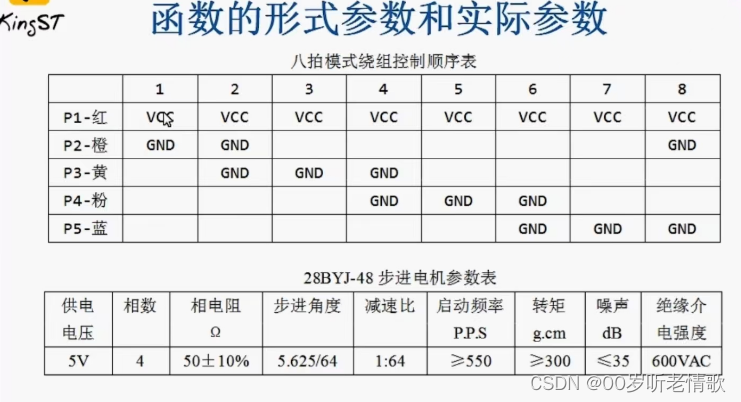
#循循渐进学51单片机#步进电机与蜂鸣器#not.8
1、能够理解清楚单片机IO口的结构。 2)t1相当于PnP三级管,t2相当于npn三极管 3) 强推挽io具有较强的驱动能力,电流输出能力很强。 2、能够看懂上下拉电阻的电路应用,并且熟练使用上下拉电阻。 3、理解28BYJ-48减速步进电机的工作…...
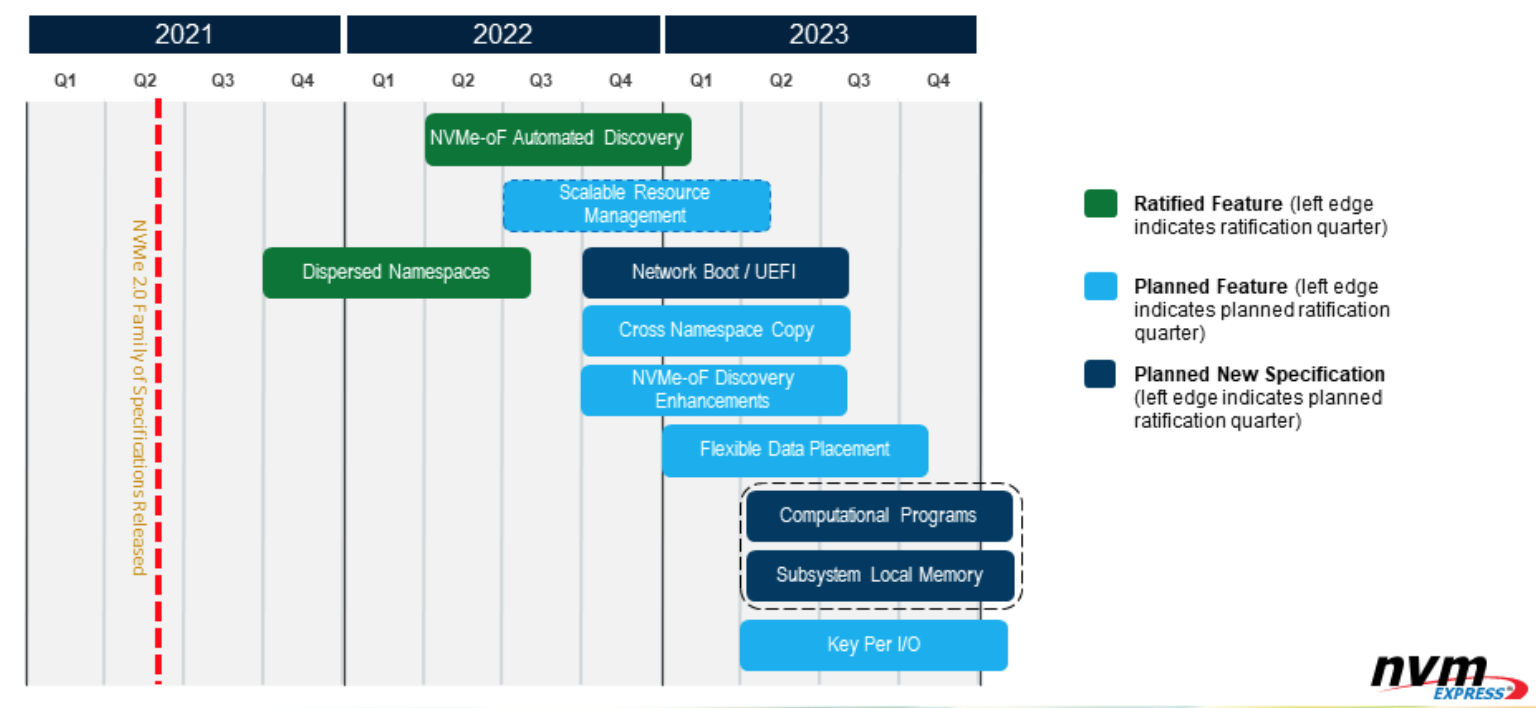
计算存储是不是智算时代的杀手锏?
想象一下,在一个繁忙的数据中心里,有一家大型互联网公司叫做“数据中心的故事”。这家公司一直在使用传统的CPU架构来处理海量数据。但是随着数据量的不断增长,CPU架构遇到了很多问题和瓶颈,这让“数据中心的故事”感到非常苦恼。…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
