代码随想录 动态规划Ⅴ
494. 目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
思路:
从数组里的元素->物品的价值,target->背包的容量。因为有正负,所以商品的价值可正客负。与昨天类似,可以先将所有的数看成正数,那么,每将一个数的符号改为负数,总数就减少到 totalsum - 2nums[i], 这道题目就转换成,通过修改符号使得 totalsum变为target的选择数目。
既然如此,就可以将这道题看作背包问题。(totalsum - target)// 2 就是背包的容量,nums[i]就是物品的体积。求使用nums[i]填满背包的方法数。
那么,dp[i]的定义就是 填满容量为i的背包的方法数,转移方程为 dp[i] += dp[i - nums[j]] , 先遍历 物品(nums数组),再倒序遍历容量(dp数组),最后返回dp[target].
根据题意,当 totalsum 小于 target 时,方法数一定为0,当(totalsum - target)% 2 == 1时,方法数一定为0(因为2nums[i] 一定为偶数)。当target为0,且totalsum满足上列要求是,一定可以找到且只能找到一个方法满足条件,故dp[0]=1
python:
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:totalsum = sum(nums)if totalsum < target:return 0if (totalsum - target) % 2 == 1:return 0target_num = (totalsum - target) // 2dp = [0 for _ in range(target_num + 1)]dp[0] = 1for num in nums:for i in range(target_num, num-1, -1):dp[i] += dp[i - num]return dp[target_num]474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2
思路:可以把这道题看作是二维的01背包,字符串数组的字符串的0和1的个数就是二维的空间。动态规划数组 dp[i][j] 表示 背包容量为 m = i,n = j 时的的最大子集长度,转移方程为 dp = max( dp[i][j], dp[ i - 字符串0的个数, j - 字符串1的个数] + 1)
class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:dp = [[0] * (n + 1) for _ in range(m + 1)] # 遍历物品for s in strs:ones = s.count('1') zeros = s.count('0') # 遍历背包容量且从后向前遍历for i in range(m, zeros - 1, -1):for j in range(n, ones - 1, -1):dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1) return dp[m][n]相关文章:

代码随想录 动态规划Ⅴ
494. 目标和 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添加 - …...
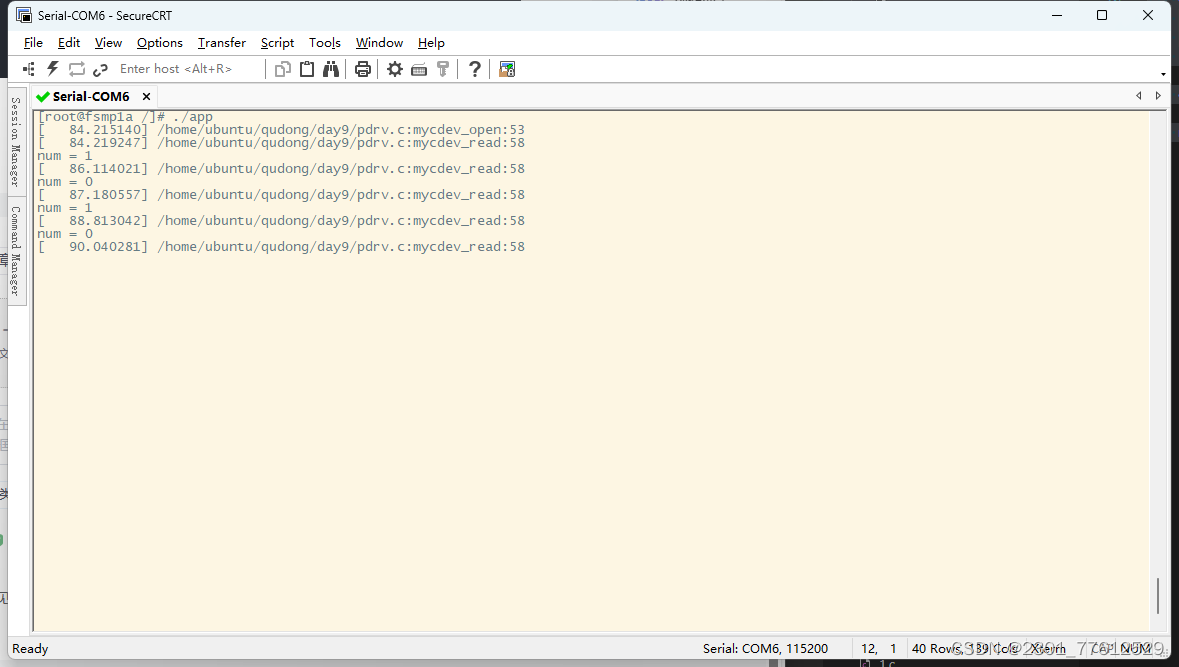
驱动DAY9
驱动文件 #include <linux/init.h> #include <linux/module.h> #include <linux/of.h> #include <linux/of_gpio.h> #include <linux/gpio.h> #include <linux/fs.h> #include <linux/io.h> #include <linux/device.h> #incl…...

03贪心:摆动序列
03贪心:摆动序列 376. 摆动序列 局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。 整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。…...

javascript获取元素在浏览器中工作区域的左、右、上、下距离,或带滚动条的元素在页面中的大小
//获取元素在包含元素框中的大小 //第1个函数为获取元素在包含元素中左内边框的距离 function getELementLeft(element){//获取元素在包含元素左边距离var actualeftelement.offsetLeft;//获取元素的上级包含元素var currentelement.offsetParent;//循环到一直没有包含元素whil…...
VSCode 安装使用教程 环境安装配置 保姆级教程
一个好用的 IDE 不仅能提升我们的开发效率,还能让我们保持愉悦的心情,这样才是非常 Nice 的状态 ^_^ 那么,什么是 IDE 呢 ? what IDE(Integrated Development Environment,集成开发环境)是含代码…...
c盘中temp可以删除吗?appdata\local\temp可以删除吗?
http://www.win10d.com/jiaocheng/22594.html C盘AppData文件夹是一个系统文件夹,里面存储着临时文件,各种应用的自定义设置,快速启动文件等。近期有用户发现appdata\local\temp占用了大量的空间,那么该文件可以删除吗?…...

Java手写聚类算法
Java手写聚类算法 1. 算法思维导图 以下是聚类算法的实现原理的思维导图,使用Mermanid代码表示: #mermaid-svg-AK9EgYRS38PkRJI4 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-AK9EgYRS38…...
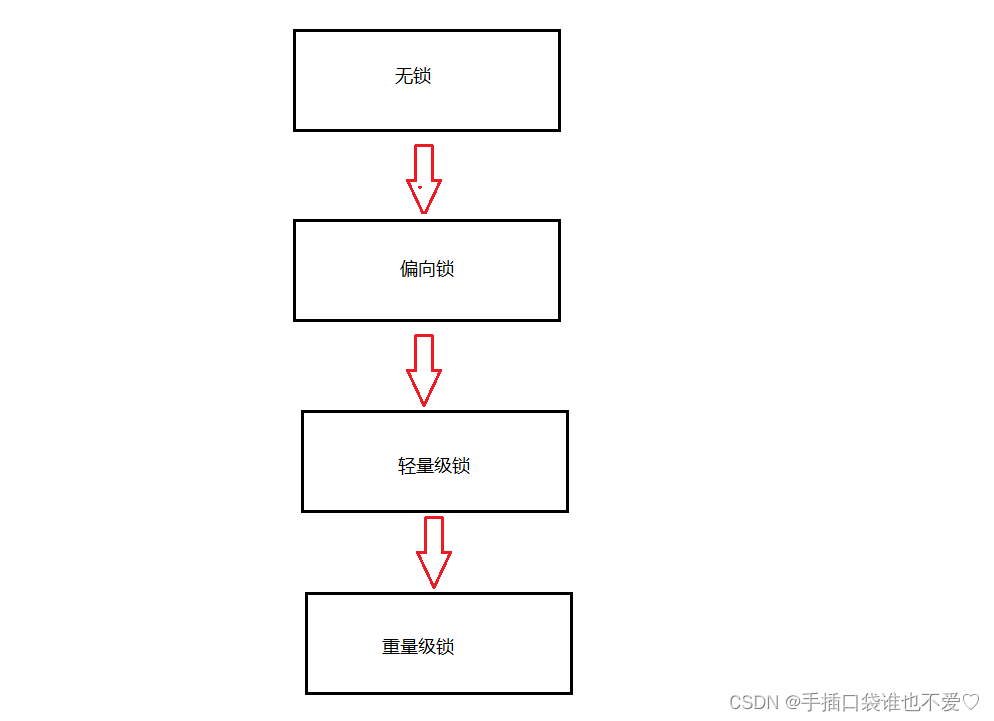
解密Java多线程中的锁机制:CAS与Synchronized的工作原理及优化策略
目录 CAS什么是CASCAS的应用ABA问题异常举例 Synchronized 原理基本特征加锁过程偏向锁轻量级锁重量级锁 其他优化操作锁消除锁粗化 CAS 什么是CAS CAS: 全称Compare and swap,字面意思:”比较并交换“,CAS涉及如下操作: 假设内存中的原数据…...

solid works草图绘制与设置零件特征的使用说明
(1)草图绘制 • 草图块 在 FeatureManager 设计树中,您可以隐藏和显示草图的单个块。您还可以查看块是欠定义 (-)、过定义 () 还是完全定义。 要隐藏和显示草图的单个块,请在 FeatureManager 设计树中右键单击草图块,…...
页面跳转后,该页面不刷新问题)
vue3使用router.push()页面跳转后,该页面不刷新问题
文章目录 原因分析最优解决 原因分析 这是一个常见问题,当使用push的时候,会向history栈添加一个新记录,这个时候,再添加一个完全相同的路由时,就不会再次刷新了 最优解决 在页面跳转时加上params参数时间 router.…...

如何理解数字工厂管理系统的本质
随着科技的飞速发展和数字化转型的推动,数字工厂管理系统逐渐成为工业4.0时代的重要工具。数字工厂系统旨在整合和优化工厂运营的各个环节,通过实时数据分析和处理,提升生产效率,降低成本,并增强企业的整体竞争力。为了…...
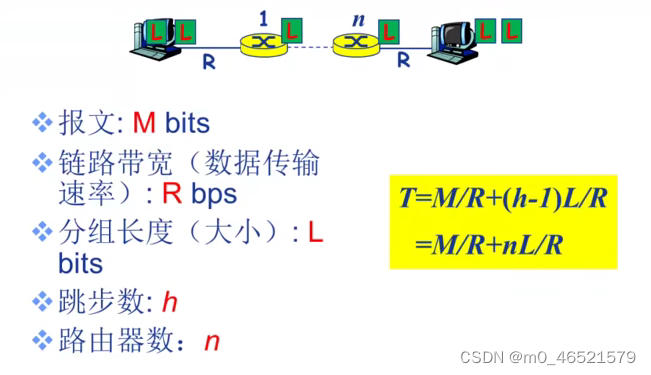
笔记1.3 数据交换
如何实现数据通过网络核心从源主机到达目的主机? 数据交换 交换网络: 动态转接动态分配传输资源 数据交换类型: (1)电路交换 (2)报文交换 (3)分组交换 电路交换的特…...
实时车辆行人多目标检测与跟踪系统(含UI界面,Python代码)
算法架构: 目标检测:yolov5 目标跟踪:OCSort其中, Yolov5 带有详细的训练步骤,可以根据训练文档,训练自己的数据集,及其方便。 另外后续 目标检测会添加 yolov7 、yolox,目标跟踪会…...

谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查;全面整理高质量的人工智能、机器学习、大数据等技术资料
🦉 AI新闻 🚀 谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查 摘要:谷歌的人工智能聊天机器人Bard发布了一项重大更新,增加了对谷歌应用的插件支持,包括 Gmail、Docs、Drive 等,并…...

NI SCXI-1125 数字量控制模块
NI SCXI-1125 是 NI(National Instruments)生产的数字量控制模块,通常用于工业自动化和控制系统中,以进行数字输入和输出控制。以下是该模块的一些主要产品特点: 数字量输入:SCXI-1125 模块通常具有多个数字…...
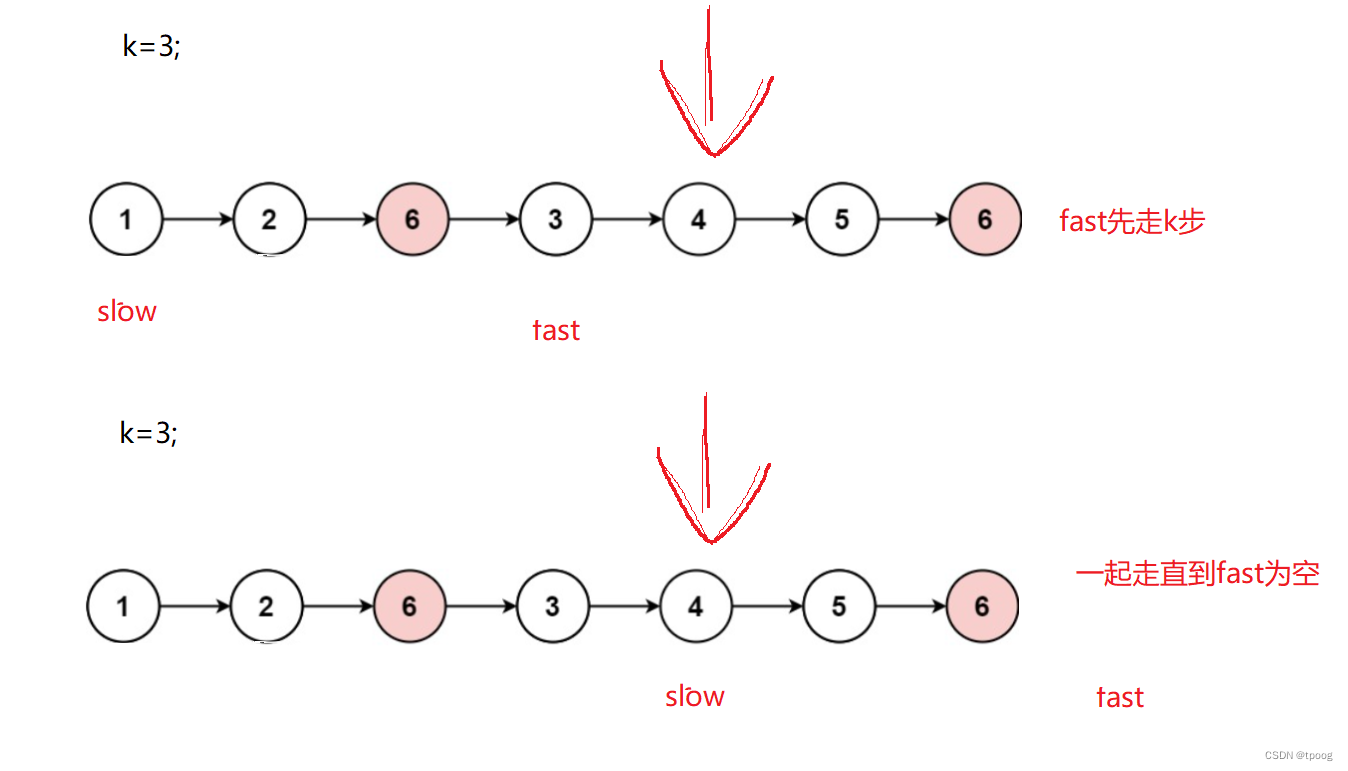
链表oj题1(Leetcode)——移除链表元素,反转链表,链表的中间节点,
链表OJ 一,移除链表元素1.1分析1.2代码 二,找到链表的中间节点2.1分析2.2代码 三,反转链表3.1分析3.2代码 四,找到链表中倒数第k个节点4.1分析4.2代码 一,移除链表元素 移除链表元素 1.1分析 这里的删除要分成两种…...
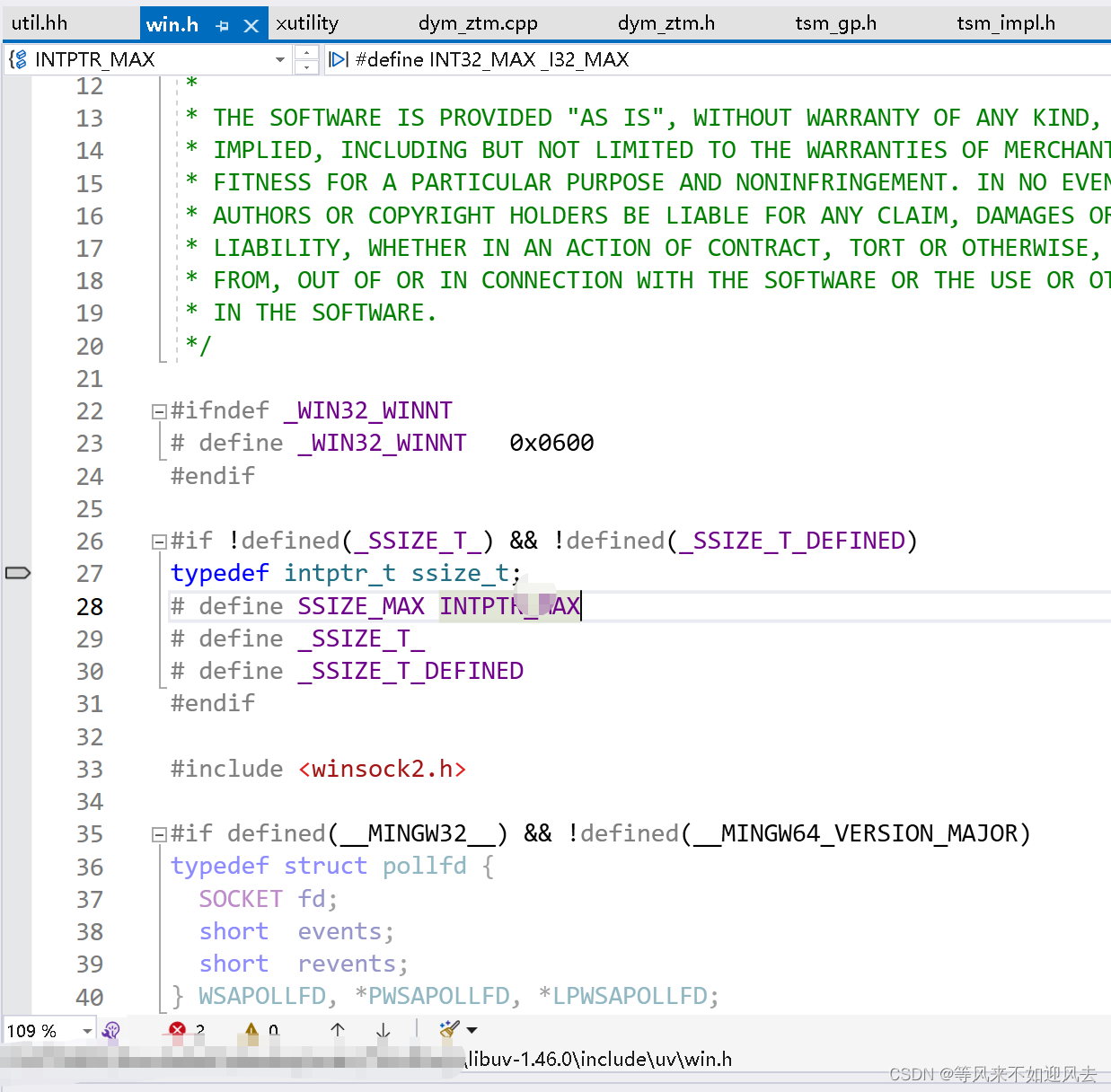
【libuv】与uvgrtrp的_SSIZE_T_定义不同
libuv的 #if !defined(_SSIZE_T_) && !defined(_SSIZE_T_DEFINED) typedef intptr_t ssize_t;...

安卓ROM定制 修改必备常识-----初步了解system系统分区文件夹的基本含义 【二】
安卓修改rom 固件 修改GSI 移植rom 必备常识 lib--**so文件基本解析 一起来了解system目录相应文件的用途吧。(rom版本不同里面的app也会不一样) 简单打开img格式后缀文件 给大家说下最简单的方法提取img里面的文件,对于后缀img格式的文件可…...

GPT会统治人类吗
一 前言 花了大概两天时间看完《这就是ChatGPT》,触动还是挺大的,让我静下来,认真地想一想,是否真正理解了ChatGPT,又能给我们以什么样的启发。 二 思考 在工作和生活中,使用ChatGPT或文心一言,…...
win系统环境搭建(六)——Windows安装nginx
windows环境搭建专栏🔗点击跳转 win系统环境搭建(六)——Windows安装nginx 本系列windows环境搭建开始讲解如何给win系统搭建环境,本人所用系统是腾讯云服务器的Windows Server 2022,你可以理解成就是你用的windows10…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
