积分值和面积、对称性
- 积分的基本含义要从积分符号说起,积分号含有加号的意思, ∫ a b f ( x ) d x \int ^b_af(x)dx ∫abf(x)dx可以理解为:区间[a,b]无限细分为无穷多个dx,无穷多个f(x)乘以dx的累积和。
- 根据上面的描述,面积可以理解为 ∫ a b ∣ f ( x ) ∣ d x , 并且 d x 为正向(即 a < b ) \int ^b_a |f(x)|dx,并且dx为正向(即a<b) ∫ab∣f(x)∣dx,并且dx为正向(即a<b)。f(x)取绝对值和dx的正向是为了保证积分表达式是正值,面积没有方向仅仅是一个标量。那么考虑一个问题:“积分值等于被积函数和积分元素x(or y)之间的面积”,这句话到底对不对呢?当然不全对。也就是说,这句话某些情况下是对的,某些情况下是错的。当被积函数的值在积分区间同号时是对的,当被积函数的值不同号时是错的,因为积分表达式f(x)dx有符号!
- 积分对称性的隐含条件也包含dx的正向。假设 f(x) 是偶函数,根据定义有f(-x) = f(x), dx大于0,则 ∫ − a a f ( x ) d x = 2 ∫ 0 a f ( x ) d x = 2 ∫ − a 0 f ( x ) d x ( 积分表达式 f ( x ) d x 处处相等 ) ( a > 0 ) \int ^{a}_{-a} f(x) dx = 2\int ^{a}_{0} f(x) dx =2 \int ^{0}_{-a} f(x) dx\color{red}(积分表达式f(x)dx处处相等)\color{black}(a>0) ∫−aaf(x)dx=2∫0af(x)dx=2∫−a0f(x)dx(积分表达式f(x)dx处处相等)(a>0);若f(x)是奇函数,根据奇函数的定义有f(-x) = - f(x),则 ∫ 0 a f ( x ) d x = − ∫ 0 a f ( − x ) d x = ∫ 0 − a f ( t ) d t ( 将 − x 带换为 t ) = − ∫ − a 0 f ( t ) d t ( a > 0 ) \int ^{a}_{0} f(x) dx =-\int ^{a}_{0} f(-x) dx = \int ^{-a}_{0} f(t) dt \color{red}(将-x带换为t)\color{black}= -\int ^{0}_{-a} f(t) dt(a>0) ∫0af(x)dx=−∫0af(−x)dx=∫0−af(t)dt(将−x带换为t)=−∫−a0f(t)dt(a>0),即可得到结论 ∫ − a a f ( x ) d x = 0 \int ^{a}_{-a} f(x) dx = 0 ∫−aaf(x)dx=0
参照下图帮助理解:
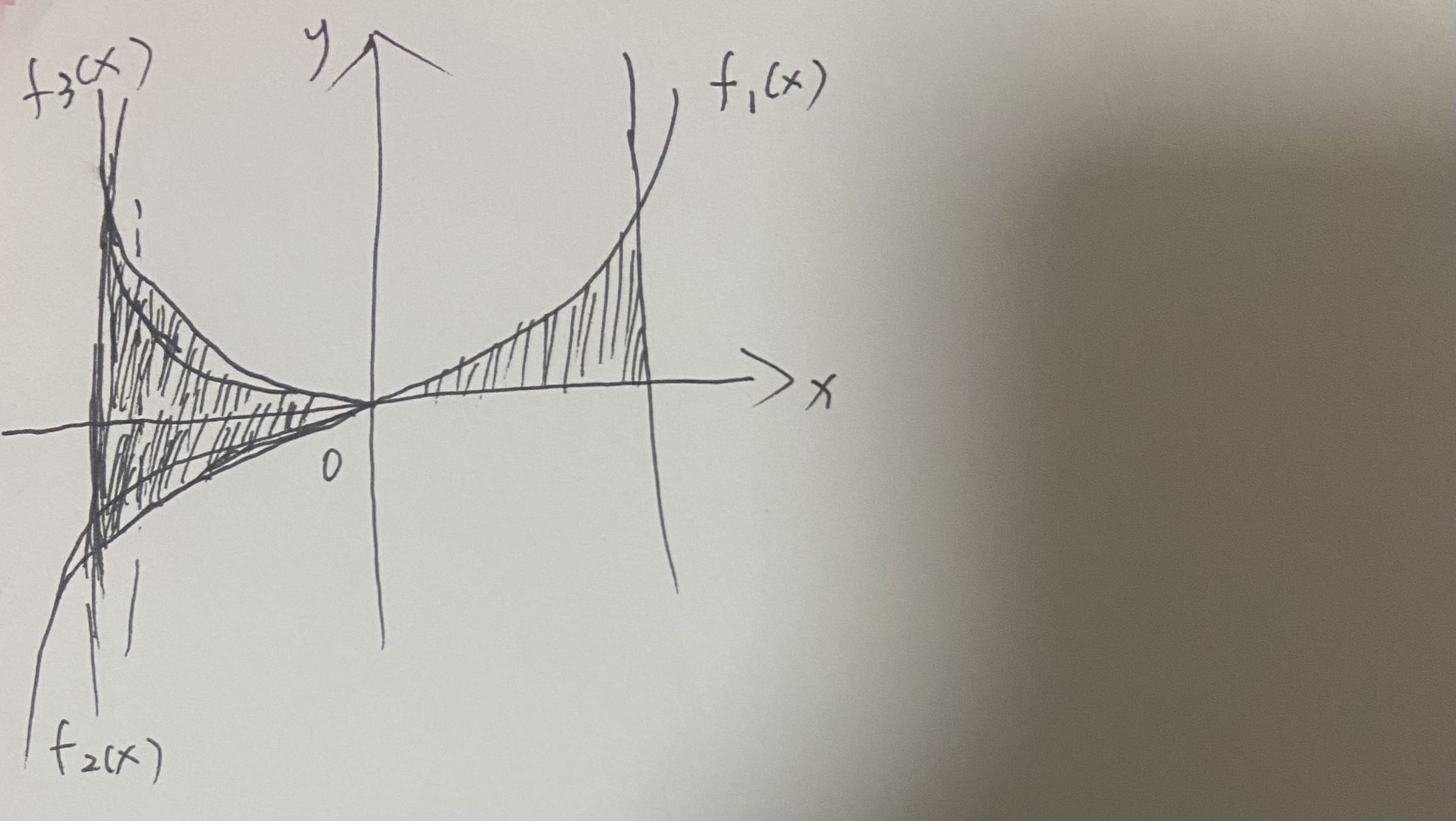
明白了这几者的关系,在碰到积分与面积、对称性有关的问题时,就不会犯迷糊了。
罗祥曾经说过一句话,“学习过于深入细节,这样的人,往往会失败,连通过考试都困难”。我觉得也是这样,学习没必要花费太多精力,牺牲自己绝大多数的精力和资源。创新讲究的是发散思维,学霸都是能集中注意力、用最少的时间获得最大收益的人。读书或者做事情过于苛刻会导致思想僵化、古板、钻牛角尖,这样的人往往只会死读书,读死书。
相关文章:

积分值和面积、对称性
积分的基本含义要从积分符号说起,积分号含有加号的意思, ∫ a b f ( x ) d x \int ^b_af(x)dx ∫abf(x)dx可以理解为:区间[a,b]无限细分为无穷多个dx,无穷多个f(x)乘以dx的累积和。根据上面的描述,面积可以理解为 ∫ a b ∣ f (…...

springboot 整合es
Spring Boot可以轻松地与Elasticsearch进行整合,以实现高效的搜索和分析功能。 以下是如何在Spring Boot应用程序中使用Elasticsearch的步骤: 1.添加依赖项 在pom.xml文件中添加以下依赖项: <dependency><groupId>org.spring…...

MyBatisPlus使用自定义JsonTypeHandler实现自动转化JSON
个人主页:金鳞踏雨 个人简介:大家好,我是金鳞,一个初出茅庐的Java小白 目前状况:22届普通本科毕业生,几经波折了,现在任职于一家国内大型知名日化公司,从事Java开发工作 我的博客&am…...

LeetCode 2097. 合法重新排列数对【欧拉通路,DFS】2650
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
学习笔记-接口测试(postman、jmeter)
目录 一、什么是接口测试 二、前端和后端 三、get请求和post请求的区别 四、cookie和session 五、接口测试的依据 六、HTTP状态码 七、通用接口用例 八、postman接口测试 九、Jmeter接口测试 一、什么是接口测试 通常做的接口测试指的是系统对外的接口,比…...
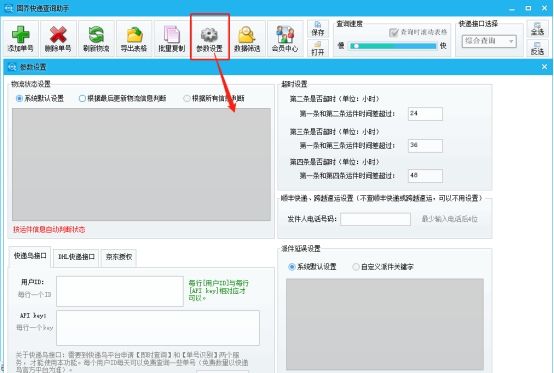
如何高效批量查询快递单号,提高工作效率?
在日常生活中,快递单号的查询是一项常规任务。过去,这项任务需要通过人工一个一个地在快递平台上查询,既耗时又费力。然而,随着科技的发展,我们有了更多的工具可以帮助我们高效地完成这项任务。本文将介绍如何使用固乔…...

12万汉语源流词典汉字记性ACCESS\EXCEL数据库
《12万汉语源流词典汉字记性ACCESS数据库》在继承前人经验的基础上,注意吸收今人的研究成果,注重形音义的密切配合,尽可能历史地、正确地反映汉字形音义的发展。在字形方面,简要说明其结构的演变。语义解释遵循古今语义的发展变化…...

深度解剖数据在队列的应用
> 作者简介:დ旧言~,目前大一,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 望小伙伴们点赞👍收藏✨加关注哟💕…...

IMX6ULL移植篇-Linux内核源码目录分析二
一. Linux内核源码目录 本文继续来具体说明 Linux内核源码的一些重要文件含义。 本文续上一篇文章,地址如下: IMX6ULL移植篇-Linux内核源码目录分析一_凌肖战的博客-CSDN博客 二. Linux内核源码目录分析 9. init 目录 此目录存放 Linux 内核启动的…...

汽车行业数据治理方案,助力车企研产供销数据一体化
随着数字技术的不断革新和应用,汽车行业已转向大数据、新技术寻求生产力突破,以电动化、网联化、智能化、共享化为标志的“汽车新四化”,为汽车行业带来了翻天覆地的变化。如何抓住“新四化”的机会,在汽车产业变革中赢得先机&…...
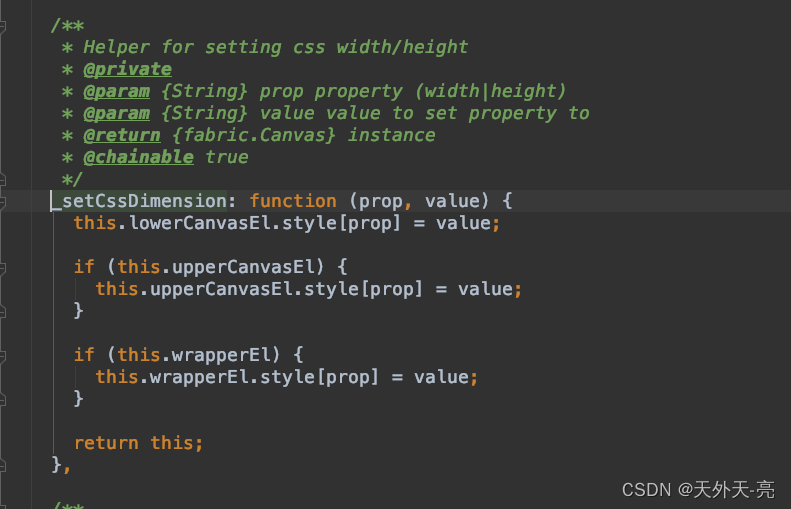
canvas-绘图库fabric.js简介
一般情况下简单的绘制,其实canvas原生方法也可以满足,比如画个线,绘制个圆形、正方形、加个文案。 let canvas document.getElementById(canvas);canvas.width 1200;canvas.height 600;canvas.style.width 1200px;canvas.style.height 6…...

代码审计——任意文件下载详解(二)
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 漏洞描述02 审计要点03 漏洞特征04 漏洞案例05 修复方案 01 漏洞描述 网站可能提供文件查看或下载的功能,如果对用户查看或下载的文件不做限制,就能够查看或下载任意的文件&…...

19异常的学习笔记
异常 很重要,有利于我们平时处理问题 异常就是代表程序出现了问题 常见的异常比如说 数组越界除法除0 异常的体系是什么 java.lang.Throwable Error Exception RuntimeException 其他异常 Error 代表的是系统级别的错误,也就是一旦系统出现问题&…...

Jenkins学习笔记4
配置构建流程: Jenkins任务创建: 1)创建新任务: 把这个Accept first connection改成 No Validation。问题得到解决。 构建触发器这块暂时没有需要配置的。 传输文件到nginx-server这个web服务器中。 将文件上传到/usr/share/n…...

自学 Java 需要具备哪些基本条件或技能?
新手初学者在自己学习Java时,需要注意两个方面,一个是学习方面,一个是知识点方面! 学习方面: 1、做学习计划并保持自律 在我们学习Java的过程中,尽量减少干扰,把自己的全部注意力集中在Java上…...
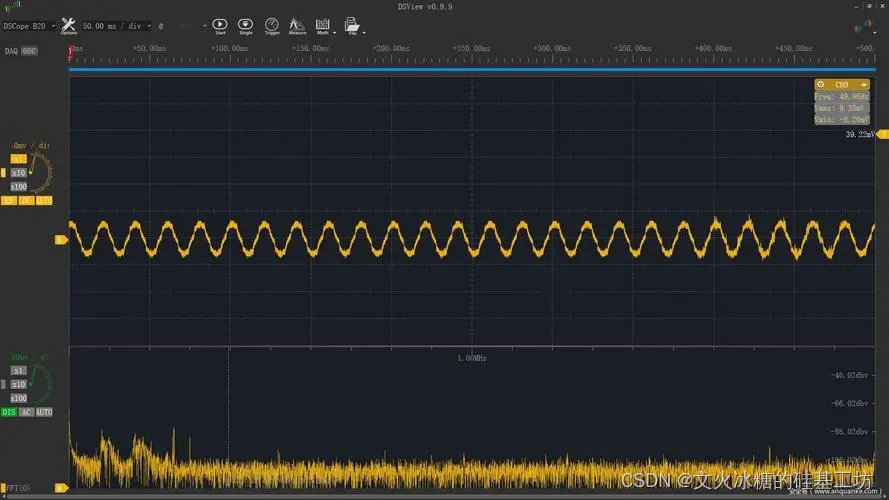
[激光原理与应用-68]:如何消除50Hz工频干扰和差分信号应对工频干扰
目录 一、什么工频干扰 1.1 什么工频干扰 1.2 工频干扰的幅度 1.3 工频干扰如何进入设备 1.4 工频干扰的负面影响 二、如何消除工频干扰 2.1 要消除工频干扰,可以考虑以下方法: 2.2 要具体消除工频干扰,可以采取以下措施 2.3 使用差…...
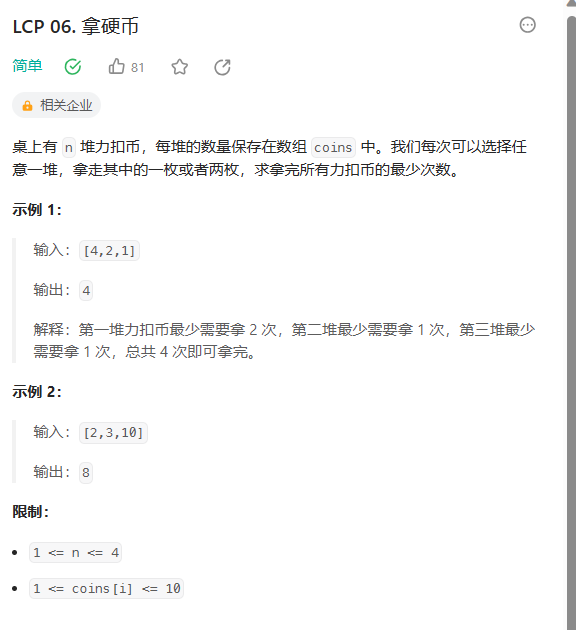
【力扣-每日一题】LCP 06. 拿硬币
class Solution { public:int minCount(vector<int>& coins) {int res0;for(auto i:coins){resi/2;res(i%2)?1:0;}return res;} };...

【JAVA-Day32】精通Java函数:定义、调用和主函数的完整指南
精通Java函数:定义、调用和主函数的完整指南 精通Java函数:定义、调用和主函数的完整指南摘要引言1. Java函数基础什么是Java函数?函数的定义和命名规则参数和返回值的概念 2. 函数的定义与语法如何声明和定义函数?函数的参数和参…...

springboot相关操作学习汇总
IDEAMAVEN apache maven 3.6.3 的安装及配置IntelliJ IDEA 安装及配置详细教程Maven下载安装及IDEA配置Maven的超详细教程 GIT 版本控制工具 - git的安装与使用gitlab上传新项目全过程 SPRINGBOOT IDEAmavenSpringboot工程创建超详细过程示例SpingBoot:整合Myb…...
如何在微信上制作自己的小程序卖东西
在当今的数字化时代,微信小程序已成为电商行业的重要平台。本文将详细解析电商微信小程序的制作流程,帮助你了解从零到上线的过程。 一、前期准备 1. 确定商城定位和目标群体:在制作电商微信小程序前,你需要明确商城的定位&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
