Leetcode算法入门与数组丨5. 数组二分查找
文章目录
- 1 二分查找算法
- 2 二分查找细节
- 3 二分查找两种思路
- 3.1 直接法
- 3.2 排除法
1 二分查找算法
二分查找算法是一种常用的查找算法,也被称为折半查找算法。它适用于有序数组的查找,并通过将待查找区间不断缩小一半的方式来快速定位目标值。
算法思想如下:
- 首先,确定待查找数组的起始位置(通常为数组的第一个元素)和结束位置(通常为数组的最后一个元素)。
- 然后,计算待查找区间的中间位置,即将起始位置和结束位置相加除以2。
- 比较中间位置的元素与目标值的大小关系:
- 如果中间位置的元素等于目标值,则查找成功,返回中间位置。
- 如果中间位置的元素大于目标值,则目标值可能在左半部分,将结束位置更新为中间位置的前一个位置。
- 如果中间位置的元素小于目标值,则目标值可能在右半部分,将起始位置更新为中间位置的后一个位置。
- 重复步骤2和步骤3,直到找到目标值或者待查找区间为空(起始位置大于结束位置)为止。
二分查找算法的时间复杂度为 O ( log n ) O(\log n) O(logn) ,其中 n n n 为数组的大小。由于每次查找都将待查找区间缩小一半,因此它比线性查找算法更加高效。
2 二分查找细节
区间开闭问题
- 左闭右闭区间:注意初始化时, r i g h t = l e n ( n u m s ) − 1 right = len(nums)-1 right=len(nums)−1,数组最后一个元素位置。
- 左闭右开区间:注意初始化时, r i g h t = l e n ( n u m s ) right = len(nums) right=len(nums),数组最后一个元素的下一个位置。
- 一般情况,全部使用「左闭右闭区间」这种写法。
m i d mid mid 取值问题
常见的两种取值公式
mid = (left + right) // 2 # 使用较多
mid = (left + right + 1) // 2
- 当待查找区间中的元素个数为奇数个,使用这两种取值公式都能取到中间元素的下标位置。
- 当待查找区间中的元素个数为偶数个
mid = (left + right) // 2能取到中间靠左边元素的下标位置。mid = (left + right + 1) // 2能取到中间靠右边元素的下标位置。
出界条件的判断
两种判断方式
left <= right
left < right
left <= right,并且查找的元素不在有序数组中,则while语句的出界条件是left > right,也就是left == right + 1,写成区间形式就是 [ r i g h t + 1 right+1 right+1, r i g h t right right],此时待查找区间为空,待查找区间中没有元素存在,此时终止循环时,可以直接返回 −1。left < right,并且查找的元素不在有序数组中,则while语句出界条件是left == right,写成区间形式就是 [ r i g h t right right, r i g h t right right]。此时区间不为空,待查找区间还有一个元素存在,我们并不能确定查找的元素不在这个区间中,此时终止循环时,如果直接返回 −1 就是错误的。
使用 left < right 的话,可以在出界之后增加一层判断,判断是否等于目标元素。
# ...while left < right:# ...return left if nums[left] == target else -1
此时,在跳出循环的时候,一定是 left == right,无需判断此时应该返回 left or right
搜索区间范围的选择
三种写法
left = mid + 1,right = mid - 1
left = mid + 1 ,right = mid
left = mid,right = mid - 1
具体哪一种写法和二分查找的两种思路有关。
- 思路 1:「直接法」—— 在循环体中找到元素后直接返回结果。
- 思路 2:「排除法」—— 在循环体中排除目标元素一定不存在区间。
3 二分查找两种思路
3.1 直接法
- 设定左右边界为数组两端,即 l e f t = 0 , r i g h t = l e n ( n u m s ) − 1 left=0,right=len(nums)−1 left=0,right=len(nums)−1,代表待查找区间为 [ l e f t , r i g h t ] [left,right] [left,right](左闭右闭区间)。
- 取两个节点中心位置 m i d mid mid ,先比较中心位置值 n u m s [ m i d ] nums[mid] nums[mid] 与目标值 t a r g e t target target 的大小。
- 如果 t a r g e t = = n u m s [ m i d ] target==nums[mid] target==nums[mid],则返回中心位置。
- 如果 t a r g e t > n u m s [ m i d ] target>nums[mid] target>nums[mid] ,则将左节点设置为 m i d + 1 mid+1 mid+1,然后继续在右区间 [ m i d + 1 , r i g h t ] [mid+1,right] [mid+1,right] 搜索。
- 如果 t a r g e t < n u m s [ m i d ] target<nums[mid] target<nums[mid],则将右节点设置为 m i d − 1 mid−1 mid−1,然后继续在左区间 [ l e f t , m i d − 1 ] [left,mid−1] [left,mid−1] 搜索。
- 如果左边界大于右边界,查找范围缩小为空,说明目标元素不存在,此时返回 −1。
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1# 在区间 [left, right] 内查找 targetwhile left <= right:# 取区间中间节点mid = left + (right - left) // 2# 如果找到目标值,则直接范围中心位置if nums[mid] == target:return mid# 如果 nums[mid] 小于目标值,则在 [mid + 1, right] 中继续搜索elif nums[mid] < target:left = mid + 1# 如果 nums[mid] 大于目标值,则在 [left, mid - 1] 中继续搜索else:right = mid - 1# 未搜索到元素,返回 -1return -1
3.2 排除法
- 设定左右边界为数组两端,即 l e f t = 0 , r i g h t = l e n ( n u m s ) − 1 left=0,right=len(nums)−1 left=0,right=len(nums)−1,代表待查找区间为 [ l e f t , r i g h t ] [left,right] [left,right](左闭右闭区间)。
- 取两个节点中心位置 m i d mid mid ,比较中心位置值 n u m s [ m i d ] nums[mid] nums[mid] 与目标值 t a r g e t target target 的大小,先将目标元素一定不存在的区间排除。
- 然后在剩余区间继续查找元素,继续根据条件排除目标元素一定不存在的区间。
- 直到区间中只剩下最后一个元素,然后再判断这个元素是否是目标元素。
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1# 在区间 [left, right] 内查找 targetwhile left < right:# 取区间中间节点mid = left + (right - left) // 2# nums[mid] 小于目标值,排除掉不可能区间 [left, mid],在 [mid + 1, right] 中继续搜索if nums[mid] < target:left = mid + 1 # nums[mid] 大于等于目标值,目标元素可能在 [left, mid] 中,在 [left, mid] 中继续搜索else:right = mid# 判断区间剩余元素是否为目标元素,不是则返回 -1return left if nums[left] == target else -1
- 直接法:更适合解决简单题目,数组中是非重复元素。
- 排除法:更适合解决复杂题目,数组里可能不存在的元素,找边界问题。
参考文献
- [1] https://datawhalechina.github.io/leetcode-notes/#/
—— END ——
如果以上内容有任何错误或者不准确的地方,欢迎在下面 👇 留言。或者你有更好的想法,欢迎一起交流学习~~~
更多精彩内容请前往 AXYZdong的博客
相关文章:

Leetcode算法入门与数组丨5. 数组二分查找
文章目录 1 二分查找算法2 二分查找细节3 二分查找两种思路3.1 直接法3.2 排除法 1 二分查找算法 二分查找算法是一种常用的查找算法,也被称为折半查找算法。它适用于有序数组的查找,并通过将待查找区间不断缩小一半的方式来快速定位目标值。 算法思想…...
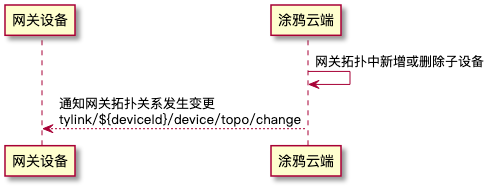
拓扑关系如何管理?
在设备对接涂鸦的云端过程中,一部分设备由于自身资源或硬件配置,无法直接连接云端。而是需要通过网关进行中转,由网关代理实现和云端进行数据交互,间接实现设备接入云端。这样的设备也称为子设备。 要想实现网关代理子设备接入云…...

vue的由来、vue教程和M-V-VM架构思想、vue的使用、nodejs
vue vue的由来 vue教程和M-V-VM架构思想 vue的初步简单使用 nodejs vue的由来 # 1 HTML(5)、CSS(3)、JavaScript(ES5、ES6、ES11):编写一个个的页面 -> 给后端(PHP、Python、Go、Java) -> 后端嵌入模板语法 -> 后端渲染完数据 -> 返回数据给前端 ->…...

课程表 循环依赖 拓扑排序 go语言
学会拓扑排序题目的基本解法 res数组 记录上课顺序g 记录学了课程i 能解锁的课程jindeg 记录每个课程的入度q 记录入度为0的课程 for循环q去解放其他课程 本题来自力扣课程表 func findOrder(numCourses int, prerequisites [][]int) []int {res : []int{}//建一个二维数组记…...

【红包雨接口设计】
一、服务器地址 http://rb.atguigu.cn 二、公共请求头参数 参数名称类型是否必选描述tokenString是用户唯一标识 备注:为了方便我们今天演示,服务端接受所有token。 三、接口 1. 创建红包雨 请求方式:GET请求地址:/api/v1/se…...

SSL证书到期更换证书会影响排名吗?
在现代的数字化时代,网络安全和用户体验成为了网站运营商和开发者们需要高度关注的问题。SSL证书作为一种重要的安全协议,对网站的安全性和用户信任起着至关重要的作用。然而,随着SSL证书的有效期限届满,许多网站运营商面临着更换…...

前端常用库之-JavaScript工具库lodash
文章目录 前端常用库之-JavaScript工具库lodash一、什么是lodash二、安装三、lodash使用Lodash 的 pick() 函数介绍和使用react 实例demo:pick结合...展开运算符(spread operator) 前端常用库之-JavaScript工具库lodash 一、什么是lodash 官网: https:…...
)
Linux- execve()
execve() 是 Linux/UNIX 中的 exec 函数家族中的一个,它允许进程执行一个新的程序。具体地,execve() 替换当前进程的映像为新的程序映像。 函数原型如下: int execve(const char *pathname, char *const argv[], char *const envp[]);pathn…...
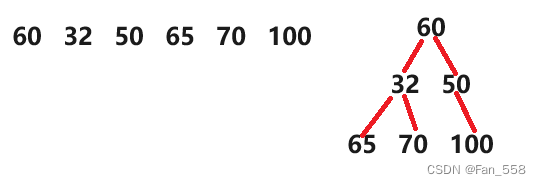
007 数据结构_堆——“C”
前言 本文将会向您介绍关于堆Heap的实现 具体步骤 tips:本文具体步骤的顺序并不是源代码的顺序 typedef int HPDataType; typedef struct Heap {HPDataType* _a;int _size;int _capacity; }Heap;初始化 void HeapCreate(Heap* hp, HPDataType* a, int n) {hp-&…...
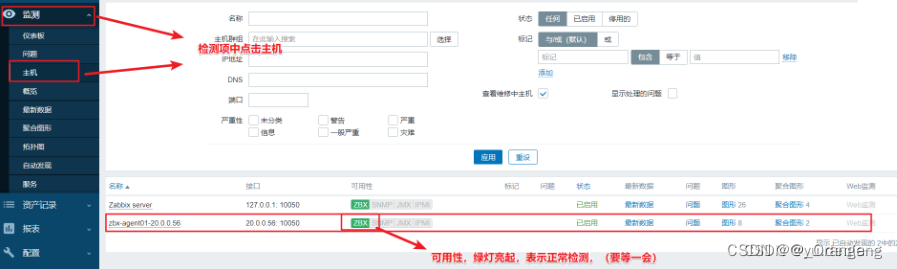
zabbix的原理与安装
一、Zabbix介绍 1、zabbix 是什么? zabbix是一个开源的IT基础监控软件,能实时监控网络服务,服务器和网络设备的状态,如网络使用,CPU负载、磁盘空间等,主要是包括数据的收集、报警和通知的可视化界面zabbi…...
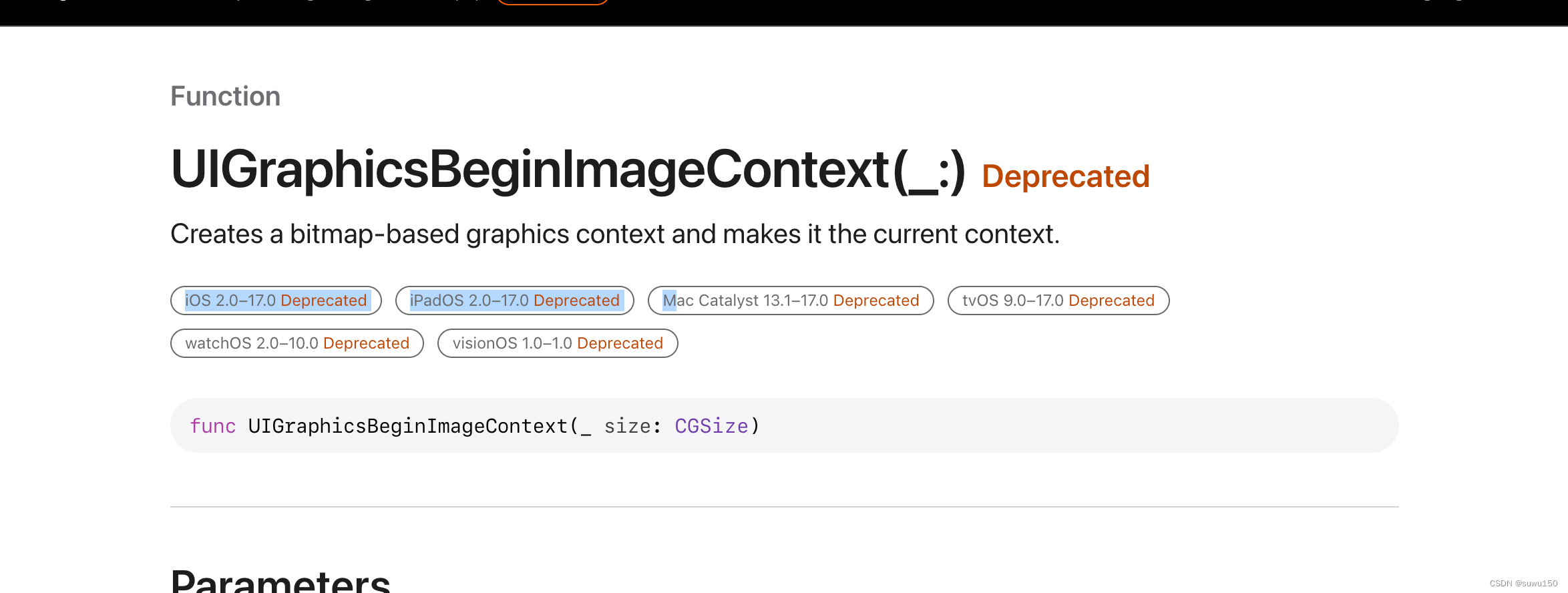
ReactNative中升级IOS 17版本Crash解决
ReactNative中升级IOS 17版本Crash解决 ReactNative中升级IOS 17版本Crash解决一、问题描述二、原因分析三、解决方案决策3.1 设置宽高为非零值3.2 使用新的UIGraphicsImageRenderer替换就版本的UIGraphicsBeginImageContext 四、可能使用到该API的三方库4.1 react-native-fast…...

MongoDB详解
一、MongoDB概述 MongoDB 是一个基于 分布式文件存储 的开源 NoSQL 数据库系统,由 C 编写的。MongoDB 提供了 面向文档 的存储方式,操作起来比较简单和容易,支持“无模式”的数据建模,可以存储比较复杂的数据类型,是一…...

【SpringCloud微服务全家桶学习笔记-服务注册zookeeper/consul】
SpringCloud微服务全家桶学习笔记 Eureka服务注册 gitee码云仓库 9.其他服务注册框架 (1)zookeeper安装与使用 zookeeper需安装在虚拟机上,建议使用CentOS,安装地址如下: zookeeper镜像源 选择第一个进入后下载ta…...

【滑动窗口】LCR 016. 无重复字符的最长子串
LCR 016. 无重复字符的最长子串 解题思路 窗口内的字符串就是不重复子串每次遇到新的字符 看看窗口内是否存在该字符 如果存在直接剔除 然后调整窗口左边界不存在 添加窗口内部 右边界 class Solution {public int lengthOfLongestSubstring(String s) {if(s.length() < …...

C++中将类成员函数作为变量传递给函数
假设类ClassName有一个成员函数 void ClassName::funcname(int);通过typedef定义一个类成员函数指针类型,参数和返回值类型都要与成员函数对应 typedef void (ClassName::*FuncPtr)(int); // 定义类成员函数指针获取到的参数就是 FuncPtr pf...

2024届数字IC设计秋招面经-鼎信
背景 985硕士,计算机科班,实验室做cpu设计和fpga算法加速,我做处理器安全方向,有项目。 投递 8.25 没有笔试,两轮面试,直接通知下周一面试,草草的准备了下。 一面 技术面 9.4 不到半小时 …...
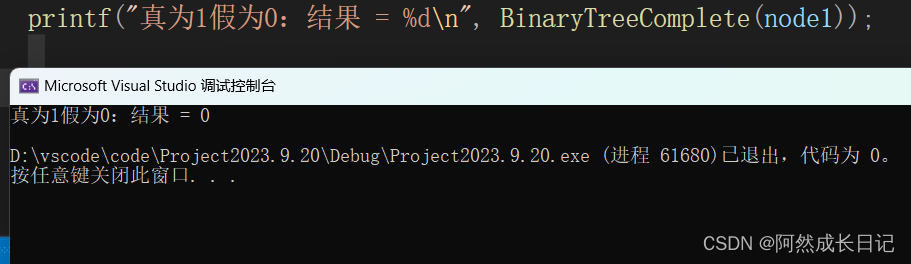
【数据结构】二叉树的节点数,叶子数,第K层节点数,高度,查找x节点,判断是否为完全二叉树等方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
和多层感知机(MLP))
前馈神经网络(FFNN)和多层感知机(MLP)
多层感知器(MLP, Multi-Layer Perceptron)和前馈神经网络(Feed-Forward Neural Network, FFNN)是深度学习中两个经常被使用的术语,它们经常被互换使用。让我们详细地了解这两个术语: 多层感知器 (MLP): M…...
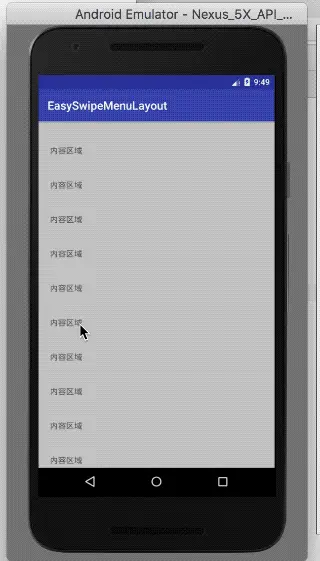
EasySwipeMenuLayout - 独立的侧滑删除
官网 GitHub - anzaizai/EasySwipeMenuLayout: A sliding menu library not just for recyclerview, but all views. 项目介绍 A sliding menu library not just for recyclerview, but all views. Recommended in conjunction with BaseRecyclerViewAdapterHelper Feature…...
优麒麟下载、安装、体验
下载 官网 优麒麟 点击增强版、或者基础版进行下载 虚拟机安装 选择镜像 修改名称和存储路径 设置为50G 下一步,点击完成 开启安装 设置语言 去掉下载更新选项 继续 点击restart now 输入密码 出现下图说明安装成功,可以畅快的使用了...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
