【算法训练-二叉树 三】【最大深度与直径】求二叉树的最大深度、求二叉树的直径
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【求二叉树的直径】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
名曲目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
求二叉树的最大深度【EASY】
求二叉树的最大深度
题干

解题思路
最大深度是所有叶子节点的深度的最大值,深度是指树的根节点到任一叶子节点路径上节点的数量,因此从根节点每次往下一层深度就会加1。因此二叉树的深度就等于根节点这个1层加上左子树和右子树深度的最大值
- 终止条件: 当进入叶子节点后,再进入子节点,即为空,没有深度可言,返回0.
- 返回值: 每一级按照上述公式,返回两边子树深度的最大值加上本级的深度,即加1.
- 本级任务: 每一级的任务就是进入左右子树,求左右子树的深度。
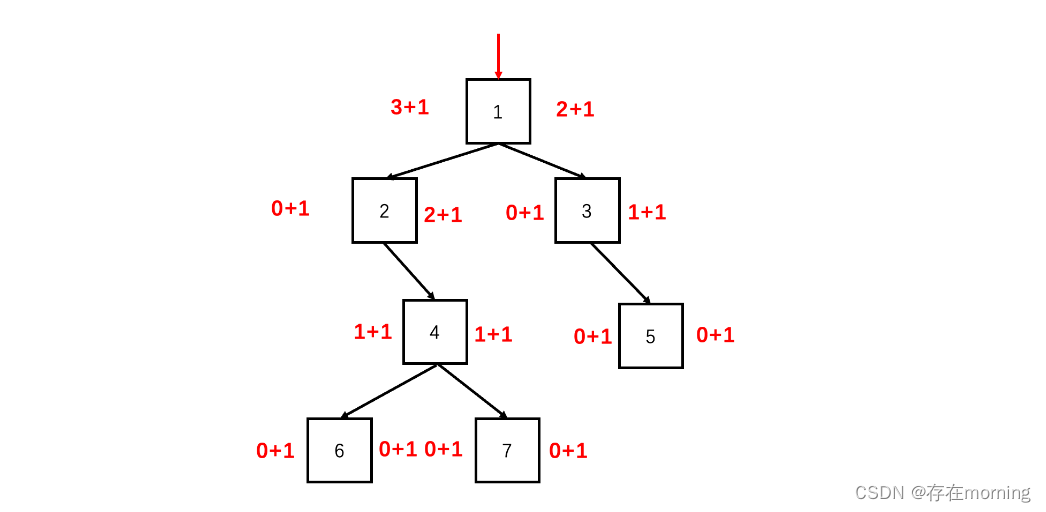
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:递归、DFS
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;/** public class TreeNode {* int val = 0;* TreeNode left = null;* TreeNode right = null;* public TreeNode(int val) {* this.val = val;* }* }*/public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param root TreeNode类* @return int整型*/public int maxDepth (TreeNode root) {// 1 如果只有根节点,返回1if (root == null) {return 0;}// 2 递归获取左子树最大深度int leftMaxLenth = maxDepth(root.left);// 3 递归获取右子树最大深度int rightMaxLenth = maxDepth(root.right);// 4 返回当前最大深度return Math.max(leftMaxLenth, rightMaxLenth) + 1;}
}
复杂度分析
时间复杂度:O(n),其中n为二叉树的节点数,遍历整棵二叉树
空间复杂度:O(n),最坏情况下,二叉树化为链表,递归栈深度最大为n
求二叉树的直径【EASY】
相对于求深度难度有所升级。
题干
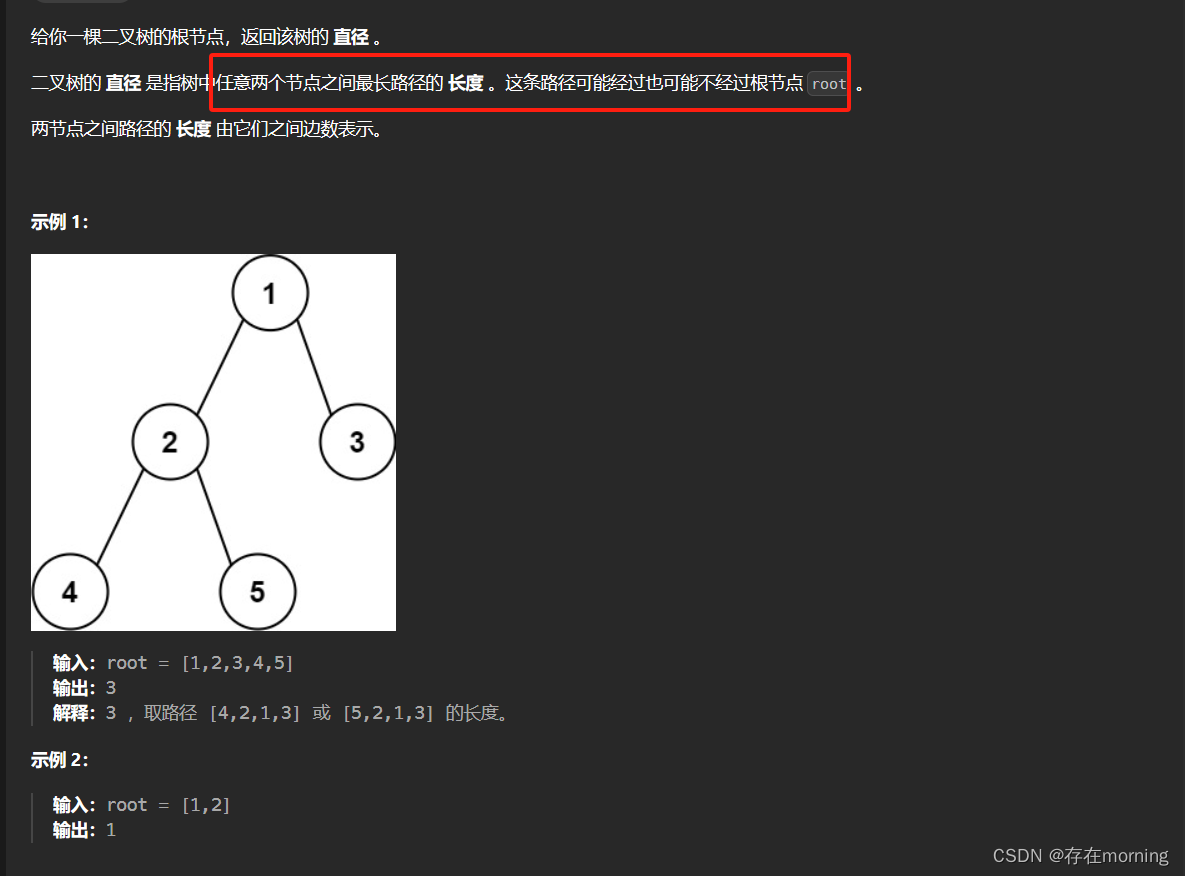
解题思路
依据题意可以得出,直径最大应该是两个叶子节点之间的路径。首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到,也就是其两边子树最大深度之和,但需要注意的是,这个节点不一定是根节点,只是直径路径上两个节点的公共节点而已
所以问题就转换成了求两个叶子节点之间最大距离的公共节点
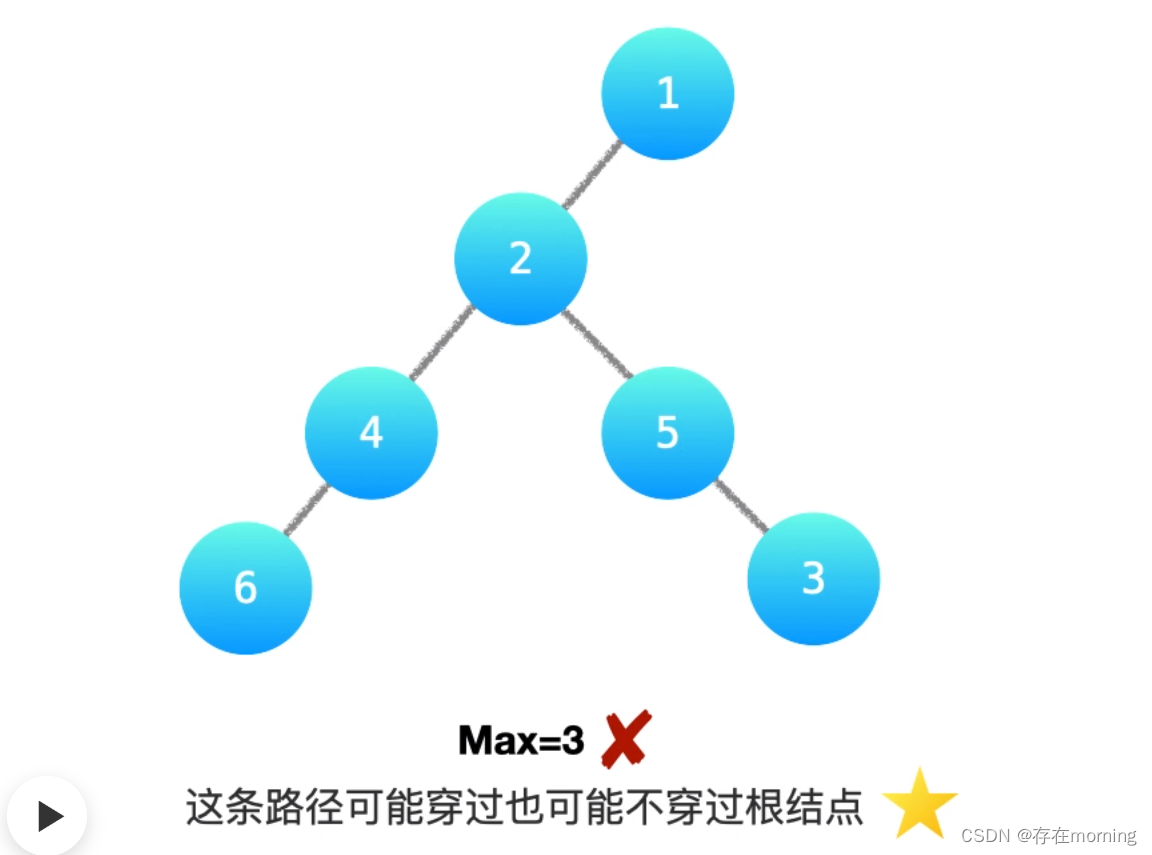
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:迭代
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
private int maxNodeNum;public int diameterOfBinaryTree(TreeNode root) {// 1 处理异常情况if (root == null) {return 0;}// 2 初始途径节点设置为1maxNodeNum = 1;// 3 递归获取根节点最大深度,过程中求最大直径maxDepth(root);// 4 全部途径节点数-1为最终结果直径return maxNodeNum - 1;}/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param root TreeNode类* @return int整型*/public int maxDepth (TreeNode root) {// 1 如果只有根节点,返回1if (root == null) {return 0;}// 2 递归获取左子树最大深度int leftMaxLenth = maxDepth(root.left);// 3 递归获取右子树最大深度int rightMaxLenth = maxDepth(root.right);// 4 直径为左右最大深度和+1(要算上根节点)int curNodeNum = leftMaxLenth + rightMaxLenth + 1;maxNodeNum = Math.max(maxNodeNum, curNodeNum);return Math.max(leftMaxLenth, rightMaxLenth) + 1;}复杂度分析
时间复杂度:遍历了整棵树节点,时间复杂度为O(N)
空间复杂度:极端情况下,二叉树退化为链表,递归栈的深度为O(N),空间复杂度为O(N)
拓展知识:二叉树的最大深度与直径
二叉树的直径和最大深度是树结构中两个不同但相关的概念。
- 最大深度(Maximum Depth):
最大深度是指二叉树中从根节点到叶子节点的最长路径的长度。通常,可以使用递归算法来计算最大深度,如下所示的伪代码:
function maxDepth(node):if node is null:return 0leftDepth = maxDepth(node.left)rightDepth = maxDepth(node.right)return max(leftDepth, rightDepth) + 1
- 二叉树的直径(Diameter of a Binary Tree):
二叉树的直径是指二叉树中任意两个节点之间的最长路径的长度。这个路径不一定通过根节点。计算二叉树的直径通常需要通过递归来查找,可以使用以下方法:
function diameterOfBinaryTree(root):if root is null:return 0# 计算左子树的最大深度leftDepth = maxDepth(root.left)# 计算右子树的最大深度rightDepth = maxDepth(root.right)# 计算经过根节点的直径rootDiameter = leftDepth + rightDepth# 计算左子树的直径leftDiameter = diameterOfBinaryTree(root.left)# 计算右子树的直径rightDiameter = diameterOfBinaryTree(root.right)# 返回三者中的最大值return max(rootDiameter, leftDiameter, rightDiameter)
请注意,这个算法的时间复杂度较高,因为它在每个节点上都会多次计算最大深度。如果需要优化性能,可以使用动态规划或记忆化搜索来避免重复计算。
相关文章:

【算法训练-二叉树 三】【最大深度与直径】求二叉树的最大深度、求二叉树的直径
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【求二叉树的直径】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件…...

查看linux是centos还是Ubuntu
查看linux是centos还是Ubuntu 命令:cat /etc/os-release...

win10怎么关闭自动更新,这个方法你知道吗?
Windows 10 操作系统自动更新是确保系统安全性和性能的关键功能。然而,有时用户可能希望手动控制更新,因此关闭自动更新可能是一个有用的选项。在本文中,我们将介绍win10怎么关闭自动更新的两种方法,以满足用户不同的需求。 方法1…...

「语音芯片」常见的OTP芯片故障分析
OTP语音芯片是指一次性可编程语音芯片,语音只能烧写一次,适合应用在不需要修改语音、语音长度短的场合,从放音的长度上可以分为20秒、40秒、80秒、170秒、340秒。语音芯片的特点是单芯片方案、价格便宜,适合批量生产,即便是小数量…...

孩子写作业买什么样台灯合适?适合孩子读写台灯推荐
现在孩子的普遍都存在视力问题,而导致孩子近视的原因可能跟光线太强或太弱、不用的用眼习惯、长时间的过度用眼等因素有关,根据数据表明目前中国近视患者人数达到6亿多,其中儿童青少年的视力不良率甚至高达八成,所以在孩子的学习道…...

DBAPI插件开发指南
DBAPI插件开发指南 插件市场 您可以去插件市场下载插件 插件的作用 DBAPI的插件分4类,分别是数据转换插件、缓存插件、告警插件、全局数据转化插件 缓存插件 对执行器结果进行缓存,比如SQL执行器,对查询类SQL,sql查询结果进…...

线程池使用之自定义线程池
目录 一:Java内置线程池原理剖析 二:ThreadPoolExecutor参数详解 三:线程池工作流程总结示意图 四:自定义线程池-参数设计分析 1:核心线程数(corePoolSize) 2:任务队列长度(workQueue) 3:最大线程数(maximumPoolSize) 4:最…...
Puppeteer无头浏览器:开启自动化之门,掌握浏览器世界的无限可能
大概还是入门期,我曾用Puppeteer做爬虫工具以此来绕过某网站的防爬机制。近期有需求要做任意链接网页截图,像这种场景非常适合用Puppeteer完成。无头浏览器我已知的还有Selenium。 完成截图需求踩的最大的坑不是具体的逻辑代码,而是Docker部…...

Ubuntu 23.10/24.04 LTS 放弃默认使用 snap 版 CUPS 打印堆栈
导读Canonical 的开发者、OpenPrinting 的项目负责人 Till Kamppeter 今年 5 月表示,计划在 Ubuntu 23.10(Mantic Minotaur)上默认使用 Snap 版本的 CUPS 打印堆栈。 不过经过数月的测试,官方放弃了这项决定。Ubuntu 23.10&#x…...

Linux CentOS7 history命令
linux查看历史命令可以使用history命令,该命令可以列出所有已键入的命令。 这个命令的作用可以让用户或其他有权限人员,进行审计,查看已录入的命令。 用户所键入的命令作为应保存的信息将记录在文件中,这个文件就是家目录中的一…...
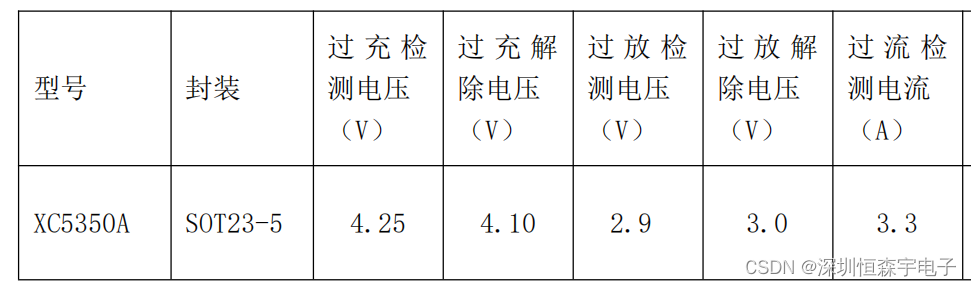
XC5350A 单节锂电池保护芯片 过放2.9V/2.8V/2.4V保护IC
XC5350A产品是一个高集成度的鲤离子/聚合物电池保护解决方案。XC5350A包含先进的功率MOSFET,高精度电压检测电路和延迟电路XC5350A放入一个超小型SOT23-5封装,只有一个外部元件使其成为在电池组有限的空间的理想解决方案。 XC5350A具有包括过充ÿ…...

单片机论文参考:1、基于单片机的电子琴
摘要 随着社会的发展进步,音乐逐渐成为我们生活中很重要的一部分,有人曾说喜欢音乐的人不会向恶。我们都会抽空欣赏世界名曲,作为对精神的洗礼。本论文设计一个基于单片机的简易电子琴。电子琴是现代电子科技与音乐结合的产物,是一…...
算法)
Opencv源码解析(2)算法
目录 一,直方图均衡 1,直方图统计 2,灰度变换 3,直方图均衡 二,可分离滤波器 1,可分离滤波器的工厂 2,ocvSepFilter、sepFilter2D 3,Sobel 三,相位相关法 phase…...
让Mac菜单栏变得更加美观整洁——Bartender 5
Bartender 5是一款Mac电脑上的菜单栏图标管理软件,能够帮助您把菜单栏上的图标整理得更加美观、整洁和易于使用。如果您的菜单栏上充斥着许多图标,导致视觉上很不舒适和疲劳,那么Bartender 5就是解决这一问题的最佳选择! Bartend…...

服务器迁移:无缝过渡指南
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

安卓开发中ViewBinding的使用
在安卓开发中,ViewBing 的作用就是简化 findViewById() 代码的写法。 看看下面的替换: etbinding.text //etfindViewById(R.id.text) 下面就看看怎么用的, 首先,打开app模块的build.gradle,然后添加如下代码&…...
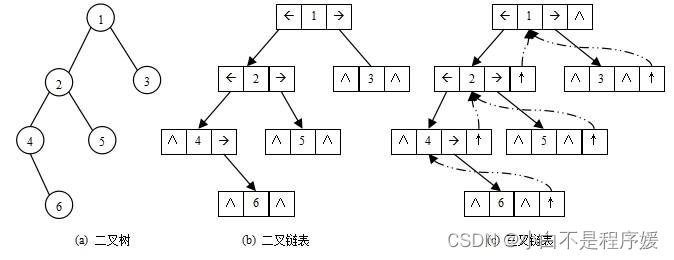
【初阶数据结构】树(tree)的基本概念——C语言
目录 一、树(tree) 1.1树的概念及结构 1.2树的相关概念 1.3树的表示 1.4树在实际中的运用(表示文件系统的目录树结构) 二、二叉树的概念及结构 2.1二叉树的概念 2.2现实中真正的二叉树 2.3特殊的二叉树 2.4二叉树的性质…...
二叉树知识点
1.霍夫曼编码 这位作者写的很清楚 哈夫曼编码详解——图解真能看了秒懂_已知字符集abcdef,若各字符出现的次数_Young_IT的博客-CSDN博客 2.满二叉树与完全二叉树 满二叉树是指每层数量是pow(2,n-1)个节点,总节点数是pow(2,n)-1; 而完全二叉树是指最后一层不一定…...
Day69:283. 移动零、11. 盛最多水的容器、42. 接雨水
283. 移动零 leetcode链接:https://leetcode.cn/problems/move-zeroes/ 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。示例 1:…...

tensorrt的安装和使用
安装 提前安装好 CUDA 和 CUDNN,登录 NVIDIA 官方网站下载和主机 CUDA 版本适配的 TensorRT 压缩包即可。 以 CUDA 版本是 10.2 为例,选择适配 CUDA 10.2 的 tar 包,然后执行类似如下的命令安装并测试: #安装c版本 cd /the/pat…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
