算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理
算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理
- 欧拉函数
- AcWing 874. 筛法求欧拉函数
- 快速幂
- AcWing 875. 快速幂
- AcWing 876. 快速幂求逆元
- 扩展欧几里德(裴蜀定理)
- AcWing 877. 扩展欧几里得算法
- AcWing 878. 线性同余方程
- 中国剩余定理
欧拉函数


互质就是两个数的最大公因数只有1,体现到代码里面就是a和b互质,则b mod a = 1 mod a (目前我不是很理解,但是可以这样理解:a和b的最大公因数是1,即1作为除数和b作为除数时,对于被除数a来说余数是一样的,即1/a的余数和b/a是一样的,即b mod a = 1 mod a)
欧拉函数的作用是求1-n与n互质的个数
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;void get_eura(int x)
{int res = x;for (int i = 2; i <= x / i; ++ i){if (x % i == 0){//res = res * (1 - 1/i);或者res = res * (i - 1) / i;都不行,前者是浮点数1 后者会溢出res = res / i * (i - 1);while (x % i == 0){x /= i;}}}if (x > 1) res = res / x * (x - 1);cout << res << endl;
}
void solve()
{int n;cin >> n;while (n -- ){int x;cin >> x;get_eura(x);}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}
AcWing 874. 筛法求欧拉函数
线性筛 + 欧拉函数(有一点推公式)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;
const int N = 1e6 + 10;
int primes[N], st[N], eulers[N];
int cnt;
void get_eulers(int x)
{eulers[1] = 1; for (int i = 2; i <= x; ++ i)//只是在线性筛的过程中顺便求了一下每个数的欧拉函数{if (!st[i])//1-n的质数{primes[cnt++] = i;eulers[i] = i - 1;}for (int j = 0; primes[j] <= x / i; ++ j)//1-n的合数//任何合数都含有质因数,4 = 1 * 2 * 1 * 2;{st[primes[j] * i] = 1;if (i % primes[j] == 0){eulers[i * primes[j]] = eulers[i] * primes[j];break;//其实也相当于一个else}//eulers[i * primes[j]] = eulers[i] * primes[j] / primes[j] * (primes[j] - 1);eulers[i * primes[j]] = eulers[i] * (primes[j] - 1);}}
}
void solve()
{int n;cin >> n;get_eulers(n);long long res = 0; for (int i = 1; i <= n; ++ i) res += eulers[i];cout << res;
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}
快速幂
1 2 4 8成指数倍增长 log的时间复杂度
AcWing 875. 快速幂
long long qmi(int a, int b, int p)
{long long res = 1;while (b){if (b & 1){res = res * a % p;}a = a * (long long)a % p;b >>= 1;}return res;
}
AcWing 876. 快速幂求逆元

欧拉函数 =>费马定理 =>快速幂实现费马定理计算结果
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <map>
#include <unordered_map>
using namespace std;long long qmi(int a, int b, int p)
{long long res = 1;while (b){if (b & 1) res = res * a % p;a = (long long)a * a % p;b >>= 1;}return res;
}
void solve()
{int n;cin >> n;while (n --){int a, p;cin >> a >> p;if (a % p == 0) cout << "impossible" << endl;else cout << qmi(a, p - 2, p) << endl;//a需要与m互质,否则a不存在乘法逆元}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}
扩展欧几里德(裴蜀定理)
AcWing 877. 扩展欧几里得算法
理解递归的本质:
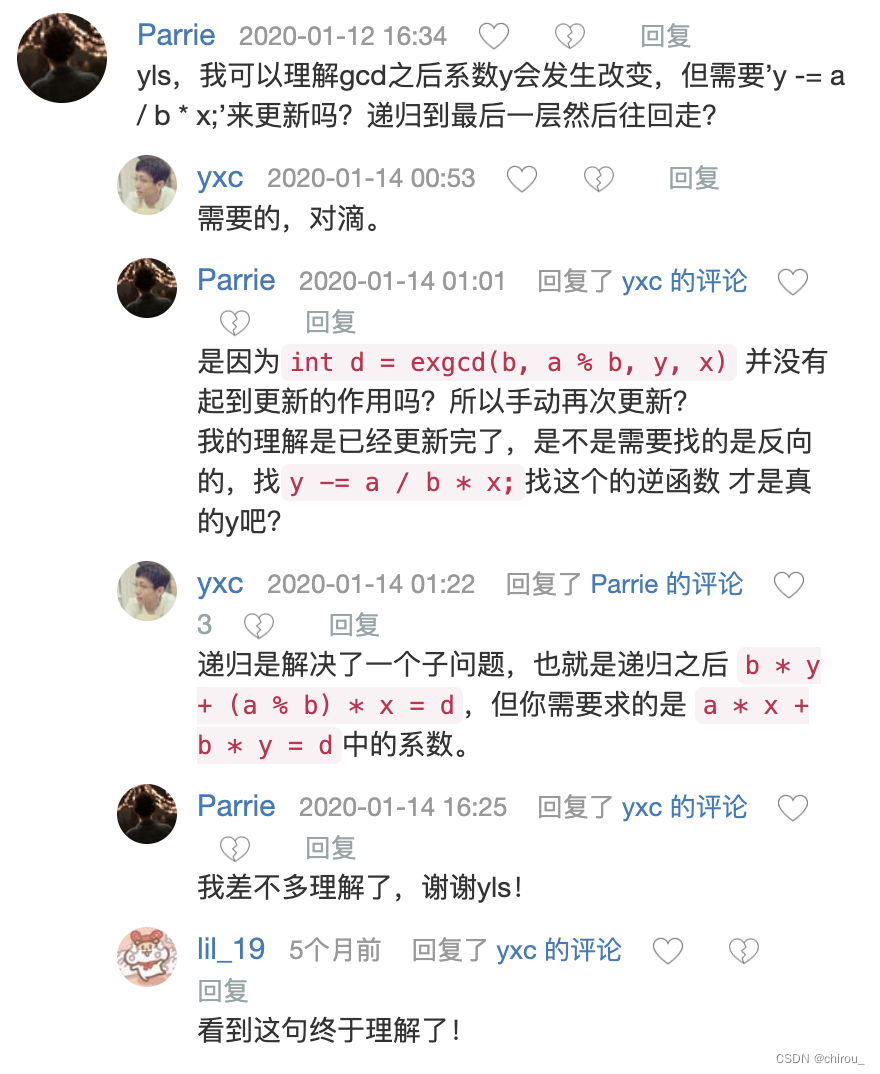
裴蜀定理和线性同余方程的证明:

#include <cstdio>
#include <iostream>using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}//d就是最大公约数,本题其实用不到int d = exgcd(b, a % b, y, x);//本题的精髓/*只是为了方便更改x和y的值,如果用d = exgcd(b, a % b, x, y);最后就解得 新x = y 新y = x - a / b * y那么代码就得这么写int t = y;y = x - a / b * y;x = t;显然比只要写一句 新y -= a / b * x; 麻烦*/y -= a / b * x;return d;
}
void solve()
{int n;cin >> n;while (n -- ){int a, b, x, y;cin >> a >> b;exgcd(a, b, x, y);cout << x << " " << y << endl;}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}
AcWing 878. 线性同余方程
线性同余方程用扩展欧几里德定理求解
本题推导过程在上面
为什么要% m
#include <cstdio>
#include <iostream>using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}else//其实不用else,上面满足直接return了,上面不满足也会走到下面 {int d = exgcd(b, a % b, y, x);y -= a / b * x;return d;}
}
void solve()
{int n;cin >> n;while (n -- ){int a, b, m, x, y;cin >> a >> b >> m;int d = exgcd(a, -m, x, y);if (b % d != 0) cout << "impossible" << endl;else cout << (long long)b / d * x % m << endl;}
}
int32_t main()
{ios::sync_with_stdio(0);cin.tie(0);int T = 1;//cin >> T;while (T --) solve();return 0;
}
中国剩余定理
相关文章:

算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理
算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理 欧拉函数AcWing 874. 筛法求欧拉函数 快速幂AcWing 875. 快速幂AcWing 876. 快速幂求逆元 扩展欧几里德(裴蜀定理)AcWing 877. 扩展欧几里得算法AcWing 878. 线性同余方程 中国剩余定理…...
ElasticSearch系列-索引原理与数据读写流程详解
索引原理 倒排索引 倒排索引(Inverted Index)也叫反向索引,有反向索引必有正向索引。通俗地来讲,正向索引是通过key找value,反向索引则是通过value找key。ES底层在检索时底层使用的就是倒排索引。 索引模型 现有索…...

【码银送书第七期】七本考研书籍
八九月的朋友圈刮起了一股晒通知书潮,频频有大佬晒出“研究生入学通知书”,看着让人既羡慕又焦虑。果然应了那句老话——比你优秀的人,还比你努力。 心里痒痒,想考研的技术人儿~别再犹豫了。小编咨询了一大波上岸的大佬ÿ…...
和本地时区(/etc/timezone))
docker容器的设置本地时间(/etc/localtime)和本地时区(/etc/timezone)
本地时区的修改 一般情况下,我们启动docker容器时指定了环境变量: -e TZ:Asia/Ho_Chi_Minh ,容器内的时区就会变成东八区,某些软件则会读取该环境变量作为其使用的时区,该环境变量相当于"残缺版"的命令&…...

侯捷老师C++课程:内存管理
内存管理 第一讲:primitives c应用程序 c内存的基本工具 测试程序: #include <iostream> using namespace std; #include <complex> #include <ext/pool_allocator.h>int main() {// 三种使用方法void* p1 malloc(512); // 512 b…...

A股风格因子看板 (2023.09 第05期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第05期,指数组合数据截止日2023-08-31,要点如下 近1年A股风格因子检验统…...
sqoop插入hbase 脚本(增量))
修炼离线:(二)sqoop插入hbase 脚本(增量)
一:mysql创建表,插入数据。 二:hbase创建表。 habse shell create aa(表名),cf(列族)三:mysql_hbase脚本。 #!/bin/shmysqlHost$1 mysqlUserName$2 mysqlUserPass$3 mysqlDbName$4 myqlTbName$5 hbaseTbName$6 hbaseTbRowkey$7…...
跨平台编程开发工具Xojo 2023 Release mac中文版功能介绍
Xojo mac是一款跨平台的软件开发工具,它允许开发人员使用一种编程语言来创建应用程序,然后可以在多个操作系统上运行。Xojo 2023是Xojo开发工具的最新版本,它提供了许多功能和改进,以帮助开发人员更轻松地构建高质量的应用程序。 …...
OpenCV Series : Target Box Outline Border
角点 P1 [0] (255, 000, 000) P2 [1] (000, 255, 000) P3 [2] (000, 000, 255) P4 [3] (000, 000, 000)垂直矩形框 rect cv2.minAreaRect(cnt)targetColor roi_colortargetThickness 1targetColor (255, 255, 255)if lineVerbose:if …...

【AD】【规则设置】设置四层板
设置四层板 一般 4层板,都会把 地 和 VCC放在内层。1、使用快捷键D-K 进入层叠管理器,添加负片层添加完后,修改层名,方便辨识修改格式:属性层号 2、进入相应layer 设置网络设置GND层设置VCC层特点:在层内可…...

Linux安装JDK1.8并配置环境变量
Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量 一、查询已有JAVA环境版本信息 java -version 二、下载Oracle JDK安装包 https://www.oracle.com/java/technologies/downloads/archive/ 三、安装 配置JDK 以下方式适用于安装各版本JDK&…...

面向面试知识--MySQL数据库与索引
面向面试知识–MySQL数据库与索引 优化难点与面试点 什么是MySQL索引? 索引的MySQL官方定义:索引是帮助MySQL快速获取数据的数据结构。 动力节点原文: MysQL官方对于索引的定义:索引是帮助MySQL高效获取数据的数据结构。 MysQL在存储数据之…...

portainer + portainer/agent
参考链接 https://docs.portainer.io/ portainer 免费版 portainer-ce 免费版 portainer-ee 企业版 portainer-agent docker本机代理 agent 下载地址 https://download.csdn.net/download/a309450028a/87451332 portainer 下载地址 https://download.csdn…...

C# 截取字符串
在 C# 中,可以使用 Substring 方法来截取字符串的一部分。该方法有两个参数:起始索引和要截取的字符数。 以下是使用 Substring 方法截取字符串的示例: string str "Hello World"; string result str.Substring(6); // 从索引为…...

FOXBORO FBM233 P0926GX控制脉冲模块
FOXBORO FBM233 P0926GX 是一种控制脉冲模块,通常用于工业自动化和控制系统中。这个模块的主要功能是生成和控制脉冲信号,以用于执行特定的操作或控制过程。以下是可能适用于 FOXBORO FBM233 P0926GX 控制脉冲模块的一些常见特点: 脉冲生成&a…...
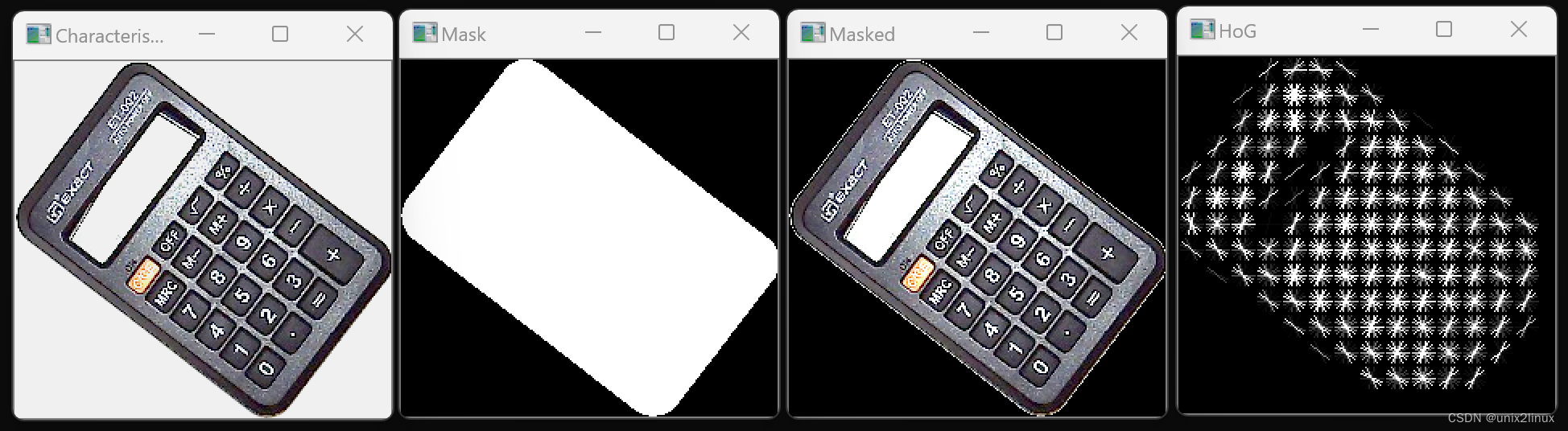
MySQL性能优化——MYSQL执行流程
MySQL 执行流程1-5如下图。 MySQL 的架构共分为两层:Server 层和存储引擎层, Server 层负责建立连接、分析和执行 SQL。MySQL 大多数的核心功能模块都在这实现,主要包括连接器,查询缓存、解析器、预处理器、优化器、执行器等。…...
Django:四、Djiango如何连接使用MySQL数据库
一、安装数据库第三方插件 安装下载mysql第三方插件 pip install mysqlclient 二、创建MySQL数据库 ORM可以帮助我们做两件事: 创建、修改、删除数据库中的表(不用写SQL语句),但无法创建数据库操作表中的数据(不用…...
LeetCode 热题 100(八):贪心。121. 买卖股票的最佳时机、45. 跳跃游戏 II
题目一: 121. 买卖股票的最佳时机https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 思路:因为时间复杂度O(n),所以使用贪心来做。类似双指针,一个指针记录到当前循环时最小的股票价格&…...
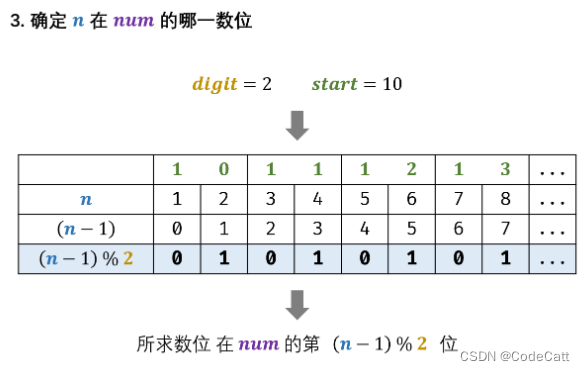
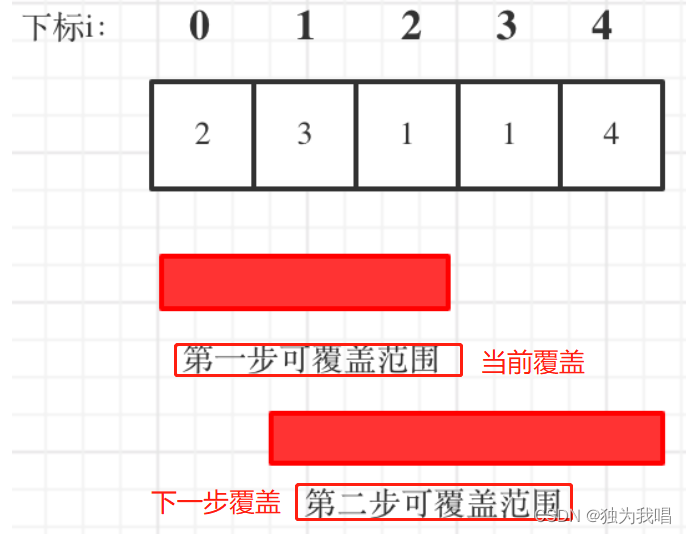
第N个数字
给你一个整数 n ,请你在无限的整数序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …] 中找出并返回第 n 位上的数字。 我觉得这题是哪以理解的 看这个题解 func findNthDigit(n int) int {digit : 1start : 1count : 9for n > count {n - countdigitstart start …...

【适用于电力系统和音频系统】计算信号的总谐波失真 (THD)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
