Golang笔试题:编写一个函数,接收一个整数参数n,输出n的阶乘结果
今天,我们开发的AI笔试题工具,ai扁食——AI程序员笔试系统给我出了中级Golang题目,就是这道题:《请编写一个函数,接收一个整数参数n,输出n的阶乘结果》,希望我写一个函数,输出n的阶乘结果。我开始的时候没觉得有什么问题,大概写了个实现如下:
// 循环计算n的阶乘
func factorial(n int) int {var result = 1for i := 1; i <= n; i++ {result *= i}return result
}或者使用递归也行:
// 计算n的阶乘
func factorial1(n int) int {if n == 1 {return 1}return n * factorial1(n-1)
}后来觉得不对,这看起来不像一个中级题目啊。
跑了个简单测试例,发现这两个实现居然在21的时候就溢出int了。
21的阶乘是-4249290049419214848
21的阶乘是-4249290049419214848哦,果然隐藏了一个考点。
那golang其实给我们提供了一个大数库:
math.Big
Big库的循环实现版本如下:
// 计算n的阶乘,使用math/big包
func factorial3(n int) *big.Int {var result = big.NewInt(1)for i := 1; i <= n; i++ {result.Mul(result, big.NewInt(int64(i)))}return result
}或者递归版本
// 计算n的阶乘,使用math/big包,递归实现
func factorial8(n int) *big.Int {if n == 1 {return big.NewInt(1)}var result = big.NewInt(int64(n))return result.Mul(result, factorial8(n-1))
}最终选择提交了循环版本,递归版本在递归深度较深的时候有非必要的消耗,循环就好。
相关文章:

Golang笔试题:编写一个函数,接收一个整数参数n,输出n的阶乘结果
今天,我们开发的AI笔试题工具,ai扁食——AI程序员笔试系统给我出了中级Golang题目,就是这道题:《请编写一个函数,接收一个整数参数n,输出n的阶乘结果》,希望我写一个函数,输出n的阶乘…...
外包干了2个月,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

无涯教程-JavaScript - BINOM.DIST函数
描述 BINOM.DIST函数返回单个项二项式分布概率。 在具有固定数量的测试或试验的问题中使用BINOM.DIST。 当任何试验的输出只是成功或失败时 试验是独立的,并且 在整个实验中成功的概率不变的情况 语法 BINOM.DIST (number_s,trials,probability_s,cumulative)争论 Argu…...

linux定时重启tomcat
1.编辑重启Tomcat命令 首先编辑一个文件 vi my_restart.sh 然后输入: #!/bin/bash . /etc/profile tomcatPath"/opt/finereport/tomcat" binPath"$tomcatPath/bin" echo "[info][$(date %F %H:%M:%S)]正在监控tomcat,路径&a…...

在静态方法中访问@Value注入的静态变量!!
一、 静态变量 static修饰的成员变量,称为静态成员变量,静态成员变量最大的特性:不属于某个具体的对象,是所有对象所共享的 简单来说:在某些类的对象中存在一些相同的成员变量,那么这种成员变量就可以设置…...

掌握这些算法,让你的编程之路更顺畅——重要算法解析
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。这些算法通常被广泛应用于日常编程工作中,是提升编程效率和解决实际问题的重要工具。本文将介绍几种十分重要的“必抓…...
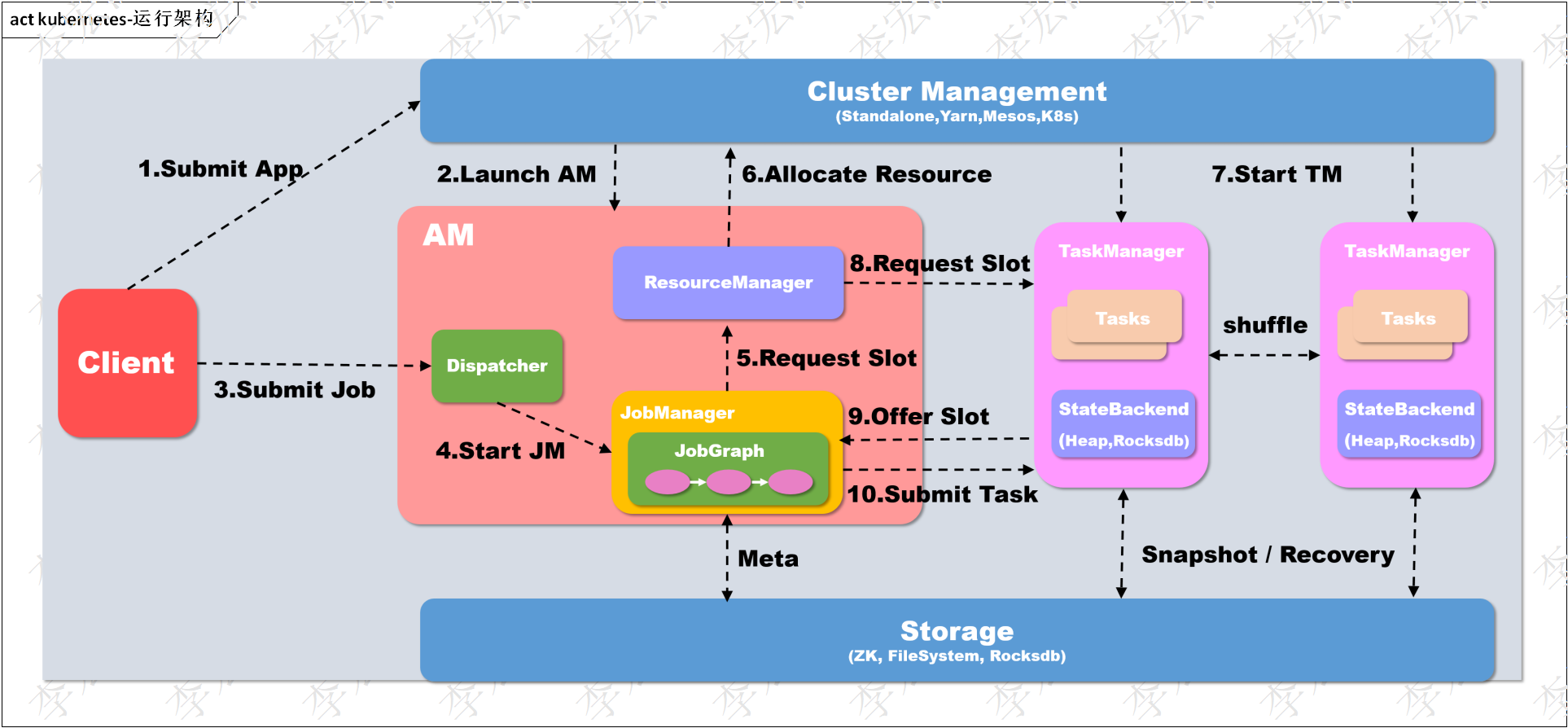
flink集群与资源@k8s源码分析-总述
1 简介 集群和资源模块提供动态资源能力,是分布式系统关键基础设施,分布式datax,分布式索引,事件引擎都需要集群和资源的弹性资源能力,提高伸缩性和作业处理能力。本文分析flink的集群和资源的k8s模块,深入了解其设计原理,为开发自有的集群和资源组件做技术准备, 同时涉…...

LeetCode 0213. 打家劫舍 II:动动态规划
【LetMeFly】213.打家劫舍 II:动动态规划 力扣题目链接:https://leetcode.cn/problems/house-robber-ii/ 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味…...
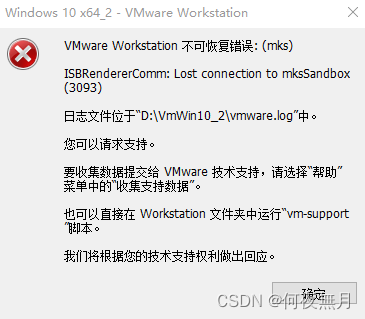
VMware17 不可恢复错误mks解决方案
用的虚拟机VMware17版本,然后运行带HDR的unity程序,结果报错 网上找了很多解决方案,都没用。毕竟需要在不放弃虚拟机3D加速的情况下运行。 最终皇天不负有心人,亲测有效的方法: 在虚拟机名字.vmx文件里添加以下2行&a…...
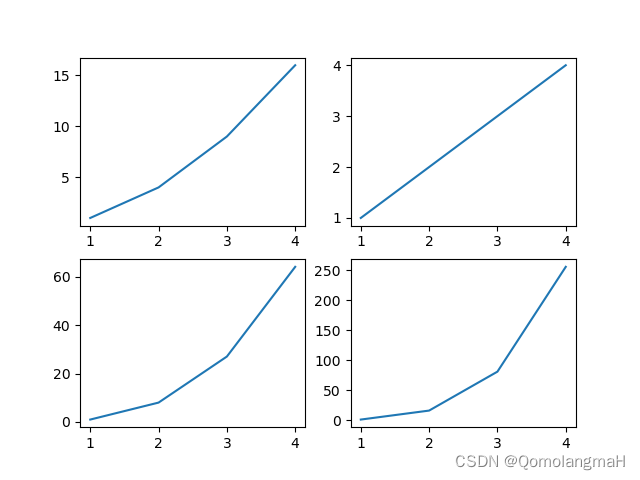
【深度学习】 Python 和 NumPy 系列教程(廿五):Matplotlib详解:3、多子图和布局:subplot()函数
目录 一、前言 二、实验环境 三、Matplotlib详解 1、2d绘图类型 2、3d绘图类型 3、多子图和布局 1. subplot()函数 简单示例 一、前言 Python是一种高级编程语言,由Guido van Rossum于1991年创建。它以简洁、易读的语法而闻名,并且具有强大的功能…...

计算机网络知识补充(1)
计算机网络:是一个将分散的,具有独立功能的计算机系统,通过通信设备和线路进行连接起来,由功能完善的软件实现资源共享和信息共享的系统,计算机网络是互连的,自治的计算机集合 互连:通过通信链路来进行互联互通 自治:没…...
C# Onnx Yolov8 Pose 姿态识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

7.algorithm2e中while怎么使用
algorithm2e中while怎么使用 在 algorithm2e 宏包中,要使用 while 循环,您可以使用 \While 和 \EndWhile 命令来定义循环的开始和结束。以下是如何使用 while 循环的示例: \documentclass{article} \usepackage[linesnumbered,boxed]{algorit…...

Flask狼书笔记 | 08_个人博客(下)
文章目录 8 个人博客8.4 初始化博客8.5 使用Flask-Login管理用户认证8.6 CSRFProtect实现CSRF保护8.7 编写博客后台小结 8 个人博客 8.4 初始化博客 1、安全存储密码 密码不要以明文的形式直接存储在数据库中,以防被攻击者盗取、泄露。一般的做法是,不…...
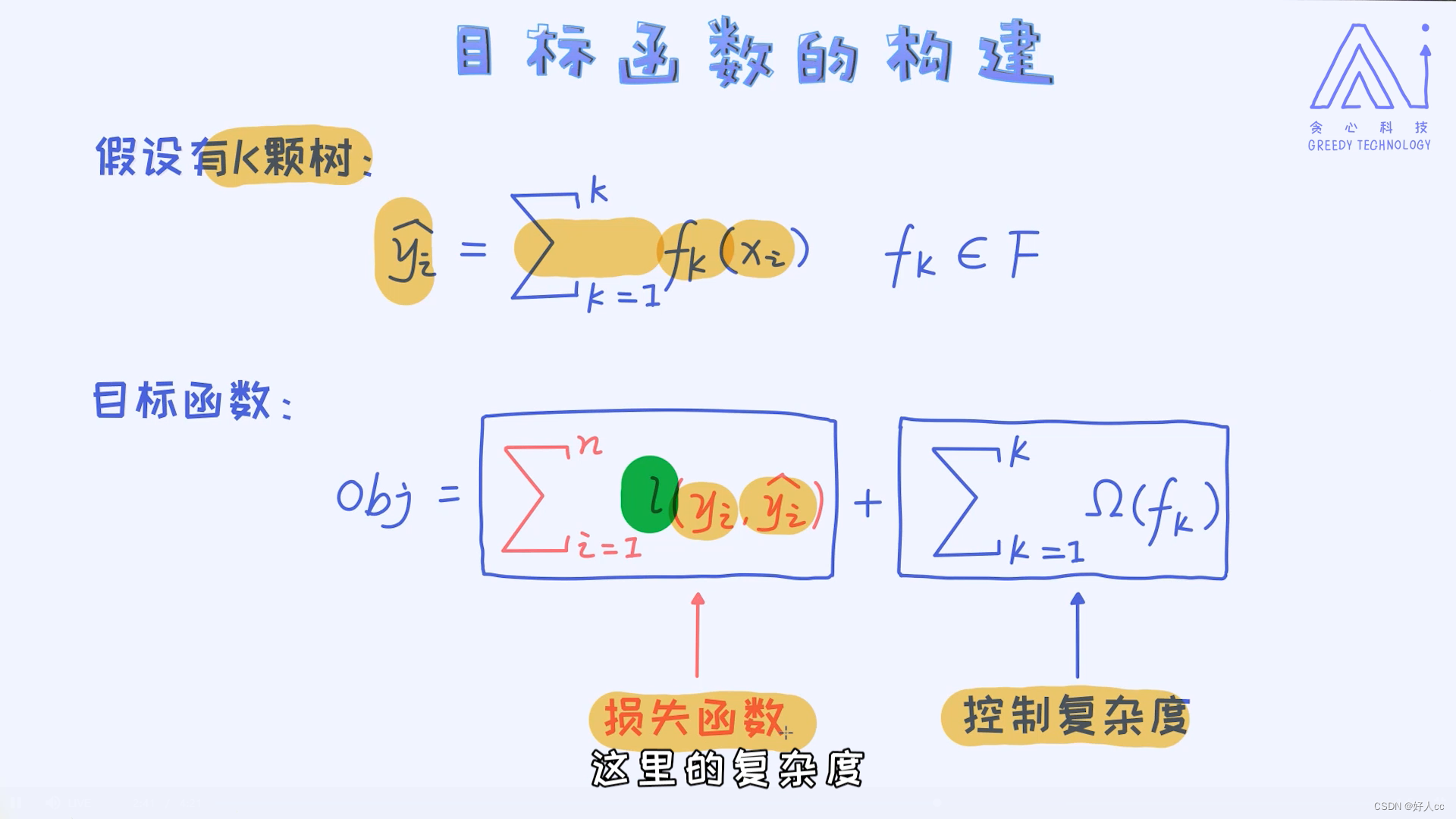
机器学习第十课--提升树
一.Bagging与Boosting的区别 在上一章里我们学习了一个集成模型叫作随机森林,而且也了解到随机森林属于Bagging的成员。本节我们重点来学习一下另外一种集成模型叫作Boosting。首先回顾一下什么叫Bagging? 比如在随机森林里,针对于样本数据,…...

react scss.modules中使用iconfont
全局引入详见全局引入scss 全局的scss文件中引入iconfont.css use "../font/iconfont.css"; 然后就可以正常使用啦...
使用Jmeter+ant进行接口自动化测试(数据驱动)
最近在做接口测试,因为公司有使用jmeter做接口测试的相关培训资料,所以还是先选择使用jmeter来批量管理接口,进行自动化测试。话不多说,进入正题: 1.使用csv文件保存接口测试用例,方便后期对接口进行维护&…...
可视化图表组件之股票数据分析应用
股市是市场经济的必然产物,在一个国家的金融领域之中有着举足轻重的地位。在过去,人们对于市场走势的把握主要依赖于经验和直觉,往往容易受到主观因素的影响,导致决策上出现偏差。如今,通过数据可视化呈现,…...
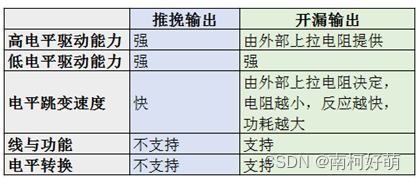
STM32 ~ GPIO不同模式之间的区别与实现原理
GPIO全称General Purpose Input Output ,即通用输入/输出。其实GPIO的本质就是芯片的一个引脚,通常在ARM中所有的I/O都是通用的。不过,由于每个开发板上都会设计不同的外围电路,这就造成了GPIO的功能可能有所不同。大部分GPIO都是…...
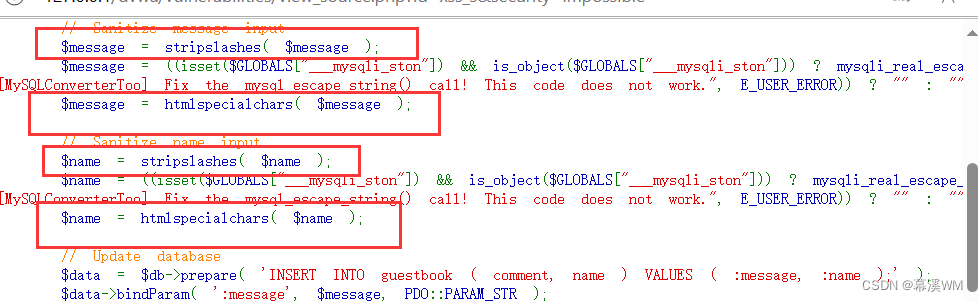
dvwa靶场通关(十二)
第十二关:Stored Cross Site Scripting (XSS)(存储型xss) low 这一关没有任何防护,直接输入弹窗代码 弹窗成功 medium 先试试上面的代码看看,有没有什么防护 发现我们的script标签不见了,应该是被过滤掉…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
