当前位置：首页 > news >正文

贝叶斯滤波计算4d毫米波聚类目标动静属性

news 2026/2/9 19:20:04

机器人学中有些问题是二值问题，对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门，机器人想判断这个门是开是关。这个二值状态是固定的，并不会随着测量数据变量的改变而改变。就像门一样，不是开就是关。

现在我利用二值贝叶斯滤波来在跟踪阶段判断4d毫米波聚类后目标的动态和静态属性

为了估计目标在给定时刻的动态概率，计算速度大于给定值的点与目标点云中的点总数的比率。在二值贝叶斯滤波器中使用贝叶斯定理来更新目标的状态，它可以是静态的，也可以是动态的，在t时刻分别用0或1的二进制值表示。

在这里插入图片描述

在这里插入图片描述
在动态和静态属性更新中， $p(x|z_t)$ 计算为速度大于给定值 $v_d$ 的点数与目标点云中的点总数的比值。

最后我们通过lt来计算二值状态的置信度：
在这里插入图片描述

明天写代码验证效果

相关文章：

贝叶斯滤波计算4d毫米波聚类目标动静属性

机器人学中有些问题是二值问题，对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门，机器人想判断这个门是开是关。这个二值状态是固定的，并不会随着测量数据变量的改变而改变。就像门…...

编程日记 2023/9/21 20:29:06

华为hcie认证考试怎么考？

华为HCIE认证考试怎么考？ 前文腾科也说了HCIE认证考试的难度会比较大，具体是难在哪里呢？华为HCIE认证的考试需要考一门笔试，笔试主要是单选、多选、判断、填空、拖拽这几个题型，考试时长一般是一个半小时，…...

编程日记 2023/9/21 20:28:06

vue +element 删除按钮操作（删除单个数据 +删除页码处理）

1.配置接口deleteItemById: "/api/goods/deleteItemById", //删除商品操作 2.get请求接口 // 删除接口后台给我们返iddeleteItemById(params){return axios.get(base.deleteItemById,{params})}3.异步请求接口 async deleteItemById(id){let res await this.…...

编程日记 2023/9/21 20:27:05

更新GitLab上的项目

更新GitLab上的项目如有需要，请参考这篇：上传项目到gitlab上 1.打开终端，进入到本地项目的根目录。 2.如果你还没有将远程GitLab仓库添加到本地项目，你可以使用以下命令： 比如： git remote add origin …...

编程日记 2023/9/21 20:26:04

K8S群集调度

K8S群集调度一、调度约束1.概述2.Pod 启动典型创建过程（工作机制 ）3.调度过程4.Predicate 的常见的算法5.常见的优先级选项6.指定调度节点： 二、亲和性1.节点亲和性2.Pod 亲和性3.键值运算关系4.示例5.Pod亲和性与反亲和性6.使用 Pod 反亲和…...

编程日记 2023/9/21 20:25:03

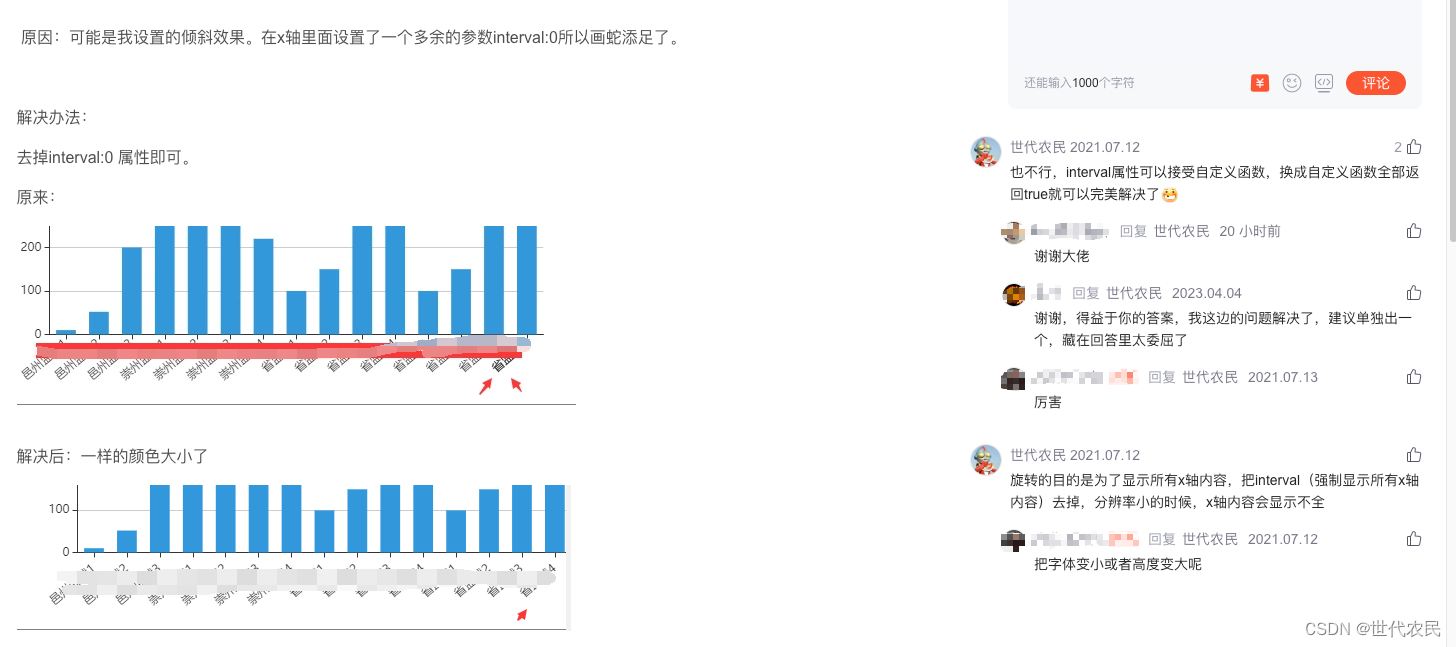
完美解决Echarts X坐标轴下方文字最后一个字体加粗颜色加深的问题

之前用Echarts画图的时候，X坐标轴最后一个字存在自动加粗的问题。也是在网上找过解决办法没有找到，后面自己研究明白了后，在某篇文章下评论了如何解决。但是好像大家没有看评论的习惯，所以单独拿出来一篇文章，希望能给…...

编程日记 2023/9/21 20:23:01

WebGL 计算平行光、环境光下的漫反射光颜色

目录光照原理光源类型平行光点光源环境光反射类型漫反射漫反射光颜色计算公式环境反射环境反射光颜色表面的反射光颜色（漫反射和环境反射同时存在时）计算公式平行光下的漫反射根据光线和法线方向计算入射角θ（以便…...

编程日记 2023/9/21 20:22:00

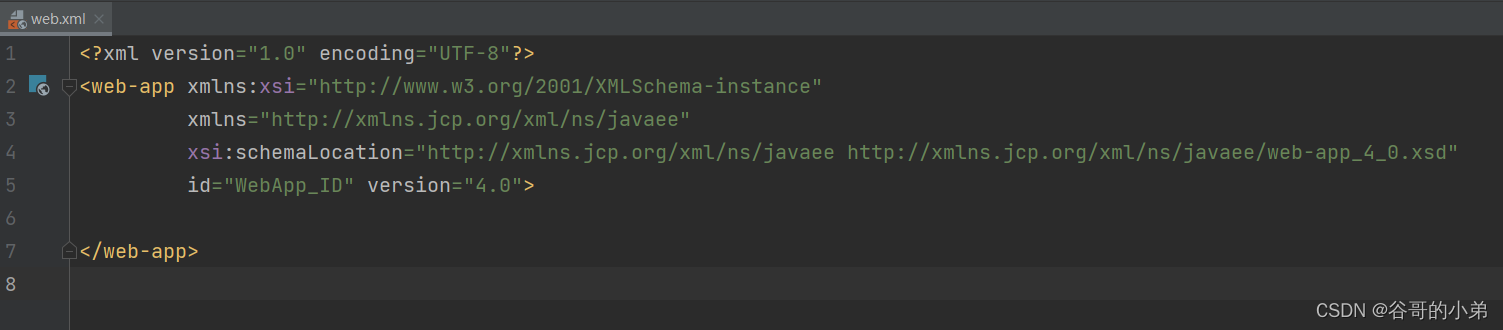
解决SpringMVC在JSP页面取不到ModelAndView中数据

版权声明本文原创作者：谷哥的小弟作者博客地址：http://blog.csdn.net/lfdfhl 问题描述 ModelAndView携带数据跳转到指定JSP页面后在该页面通过EL表达式取不到原本存放在ModelAndView中的数据。问题原因在IDEA中创建Maven工程时web.xml中默认的约束…...

编程日记 2023/9/21 20:20:59

Spring 6.0 新特性

文章目录 Spring的发展历史AOTGraalVMSpringBoot实战AOTRuntimeHints案例分析RuntimeHintsRegistrar SpringBoot中AOT核心代码 Spring的发展历史 AOT Spring 6.0的新特性Ahead of Time（AOT）编译是一种技术，可以提前将Spring应用程序编译成原…...

编程日记 2023/9/21 20:18:57

计算机竞赛深度学习+opencv+python实现昆虫识别 -图像识别昆虫识别

文章目录 0 前言1 课题背景2 具体实现3 数据收集和处理3 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数：2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 4 MobileNetV2网络5 损失函数softmax 交叉熵5.1 softmax函数5.2 交叉熵损失函数 6 优化器SGD7 学…...

编程日记 2023/9/21 20:17:57

软件过程能力成熟度评估——CSMM认证

CSMM认证又称为“软件过程能力过程成熟度评估”，由中国电子技术标准化研究院联合五十余家产学研用相关方结合我国实际，自主制定的团体标准，于2021年6月8号发布，目的是为了帮助国内软件企业对自身的软件能力进行评估和判断&#xf…...

编程日记 2023/9/21 20:15:55

学内核之二十一：系统调用栈结构分析

目录一构建分析环境二栈的位置三栈开头8字节四寄存器环境五 R4和R5 六如何确定系统调用的具体函数一构建分析环境为了分析方便，做了如下测试环境： 内核实现一个简单的创建字符设备的驱动应用层实现一个c程序，操作为打开内…...

编程日记 2023/9/21 20:13:53

互联网3.0 数字原生——数物虚实多维细粒度泛在融合

随着计算机、宽带网、通信技术的飞速发展，互联网技术和软硬件系统也不断演进，催生了一场前所未有的数字化革命。从Web1.0到Web3.0，以及虚拟现实、人工智能和数字孪生等领域的崛起，每一步都勾画出了一个崭新的数字未来，…...

编程日记 2023/9/21 20:11:50

实现AIGC更好的数据存力，这家科技巨头为我们指明了方向

存力即数据存储能力蕴藏着巨大的发展机会【全球存储观察 ｜ 热点关注】 2023年，全球被ChatGPT的热潮席卷，拥抱AIGC的创新赛道成为众多企业的新选择。全球存储观察分析指出，影响AIGC发展的三大因素也日益凸显，即算…...

编程日记 2023/9/21 20:08:47

企业如何在抖音上搞到TOB潜在精准客户流量？

我们都知道，现在互联网上流量都被集中了几个大的平台里。而抖音，一定是绕不开那个！图片在公众号：白杨SEO上去看。抖音，在很多人的传统印象里，还只是一个娱乐短视频APP，用来打发时间而已。事实…...

编程日记 2023/9/21 20:06:45

JeecgBoot v3.5.5 版本发布，性能大升级版本—开源免费的低代码开发平台

项目介绍 JeecgBoot是一款企业级的低代码平台！前后端分离架构 SpringBoot2.x，SpringCloud，Ant Design&Vue3，Mybatis-plus，Shiro，JWT 支持微服务。强大的代码生成器让前后端代码一键生成! JeecgBoot引领…...

编程日记 2023/9/21 20:05:44

与树上边权、连通块、二分块相关的问题（抓住各连通块之间的联系，考虑增量）：CF444E

https://www.luogu.com.cn/problem/CF444E 首先肯定二分然后是棵树，所以考虑按顺序枚举边权然后肯定会有连通块和并查集考虑现在场上有多个连通块，我们只保留大于 m i d mid mid 的边则每个连通块都必须往外连边一个很朴素的思路是判定每个连…...

编程日记 2023/9/21 20:04:44

解决VSCode下载速度很慢

这是VSCode的官网： Visual Studio Code - Code Editing. Redefined 按照官网的下载链接，速度实在是感人！ 解决办法也很简单，把链接换为CDN加速的链接把下载链接中的az764295.vo.msecnd.net 替换为👉 vscode.cdn.azu…...

编程日记 2023/9/21 20:03:43

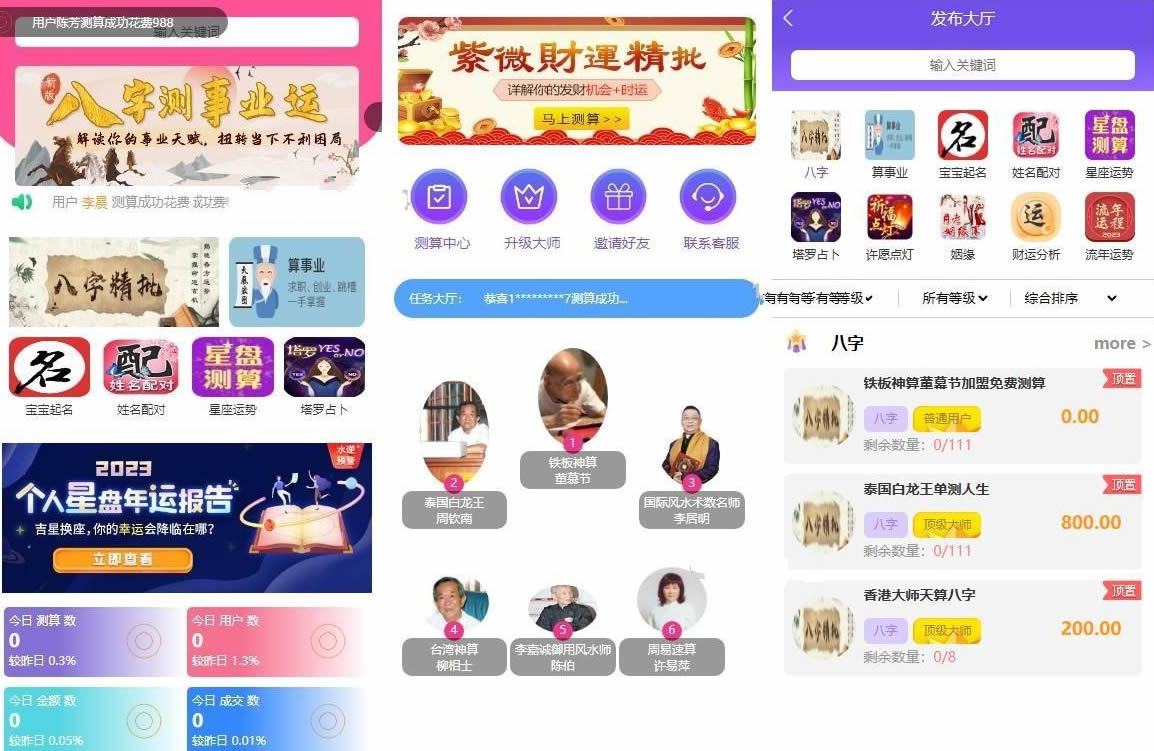
悬赏算命测算源码可以用二维码收款可以直接拿来运营

首发悬赏算命测算源码可以用二维码收款可以直接拿来运营吸金！用户可以通过发布悬赏赏金算命，也可以通过升级发布测算任务来吸金测试环境：php5.6apache2.4mysq5.6 安装教程： 测试环境：php5.6apache2.4mysq5.6 安装&…...

编程日记 2023/9/21 20:02:42

在Linux中安装nginx-1.20.1+php-7.4.28（增加扩展）

NginxPHP安装在公网IP为x.x.x.x的服务器上需要下载安装的软件版本：nginx-1.20.1php-7.4.28 需要增加的PHP扩展如下： 在编译安装php-7.4.28时加上的pcntl； 单独下载安装的Wxwork_finance_sdk；（在编译安装php-7.4.2…...

编程日记 2023/9/21 20:00:40

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言在数据驱动的背景下，知识图谱凭借其高效的信息组织能力，正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合，探讨知识图谱开发的实现细节，帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/17 21:39:04

面向无人机海岸带生态系统监测的语义分割基准数据集

描述：海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而，目前该领域仍面临一个挑战，即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

编程新知 2026/1/25 14:15:52

MySQL 8.0 事务全面讲解

以下是一个结合两次回答的 MySQL 8.0 事务全面讲解，涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容，并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解一、事务的核心概念（ACID） 事务是…...

编程新知 2025/9/19 22:12:36

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能

1. 开发环境准备安装DevEco Studio 3.1： 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置： // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

编程新知 2025/12/29 15:43:26

Ubuntu Cursor升级成v1.0

0. 当前版本低使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开，快捷键也不好用，当看到 Cursor 升级后，还是蛮高兴的 1. 下载 Cursor 下载地址：https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ，…...

编程新知 2026/2/4 16:04:11

小木的算法日记-多叉树的递归/层序遍历

🌲 从二叉树到森林：一文彻底搞懂多叉树遍历的艺术 🚀 引言你好，未来的算法大神！ 在数据结构的世界里，“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从二叉树开始入门的，它…...

编程新知 2025/11/13 14:22:52

VisualXML全新升级 | 新增数据库编辑功能

VisualXML是一个功能强大的网络总线设计工具，专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑（如DBC、LDF、ARXML、HEX等），并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

编程新知 2026/2/6 5:51:15

【把数组变成一棵树】有序数组秒变平衡BST，原来可以这么优雅！

【把数组变成一棵树】有序数组秒变平衡BST，原来可以这么优雅！ 🌱 前言：一棵树的浪漫，从数组开始说起程序员的世界里，数组是最常见的基本结构之一，几乎每种语言、每种算法都少不了它。可你有没有想过，一组看似“线性排列”的有序数组，竟然可以**“长”成一棵平衡的二…...

编程新知 2025/8/26 4:33:55

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++

关于 Reflection（反射） 这个概念，总结一下： Reflection（反射）是什么？ 反射是对类型的自我检查能力（Introspection） 可以查看类的成员变量、成员函数等信息。反射允许枚…...

编程新知 2025/12/1 1:27:24

6.计算机网络核心知识点精要手册

计算机网络核心知识点精要手册 1.协议基础篇网络协议三要素语法：数据与控制信息的结构或格式，如同语言中的语法规则语义：控制信息的具体含义和响应方式，规定通信双方"说什么"同步：事件执行的顺序与时序…...

编程新知 2025/9/26 21:47:06