【Unity3D】空间和变换
1 空间
1.1 左右手坐标系及其法则
1.1.1 左右手坐标系

Unity 局部空间、世界空间、裁剪空间、屏幕空间都采用左手坐标系,只有观察空间采用右手坐标系。
左右手坐标系除了坐标系朝向(旋向性)不同,还存在以下差异:
- 左手坐标系下旋转正方向的定义遵循左手法则,右手坐标系下旋转正方向的定义遵循右手法则;
- 左手坐标系下向量叉乘遵循左手法则,右手坐标系下向量叉乘遵循右手法则。
1.1.2 左右手法则
左手坐标系和右手坐标系下旋转正方形定义:

左手坐标系和右手坐标系下向量叉乘方向定义:
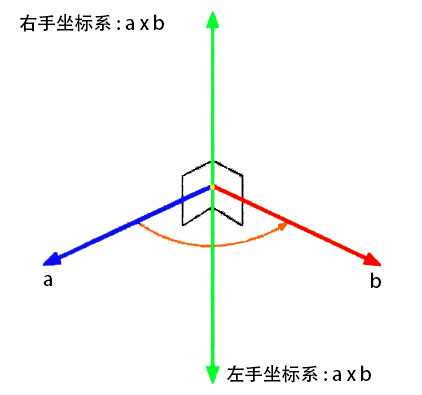
1.2 四维空间
在三维空间中,将向量 u 变换到向量 v,如果该变换是一个线性变换,一般可以使用一个不依赖于 u、v 的 3x3 的矩阵描述,即 A·u=v,其中 A 是描述该线性变换的变换矩阵。但是,并不是所有线性变换都能使用 3x3 矩阵描述,如:平移变换和对称变换,对于这些变换,需要将空间扩展到四维空间中,再使用 4x4 矩阵描述。
Unity 模型变换主要有平移、旋转、缩放、对称,其中旋转和缩放变换可以使用 3x3 矩阵描述,平移和对称变换必须使用 4x4 矩阵描述,为了统一描述这些变换,将三维空间扩展到四维空间中,扩展方法如下:
- 三维空间中的坐标原点 [0, 0, 0]' 映射到四维空间中的 [0, 0, 0, 1]' 点;
- 三维空间中的 x、y、z 轴正方向单位向量 [1, 0, 0]'、[0, 1, 0]'、[0, 0, 1]' 分别映射到四维空间中的 [1, 0, 0, 0]'、 [0, 1, 0, 0]'、 [0, 0, 1, 0]' 向量;
- 新添加的 w 轴 正方向单位向量为 [0, 0, 0, 1]'。
注意:三维空间中的原点 [0, 0, 0]' 并没有映射到四维空间中的原点 [0, 0, 0, 0],而是映射到 [0, 0, 0, 1]。
由以上空间映射关系可知:
- 三维空间中的任意点 [x, y, z]',对应的四维空间坐标为:[x, y, z, 1]';
- 三维空间中的任意向量 [x, y, z]',对应的四维空间坐标为:[x, y, z, 0]'。
1.3 Unity 空间
1.3.1 Unity 空间变换过程

- 从模型空间到裁剪空间的变换过程在顶点着色器中完成,顶点着色器输入模型局部坐标,输出裁剪空间中的坐标;
- 从裁剪空间到屏幕空间的变换过程由系统控制,用户不能控制该阶段变换。
1.3.2 Unity 空间变换示意图

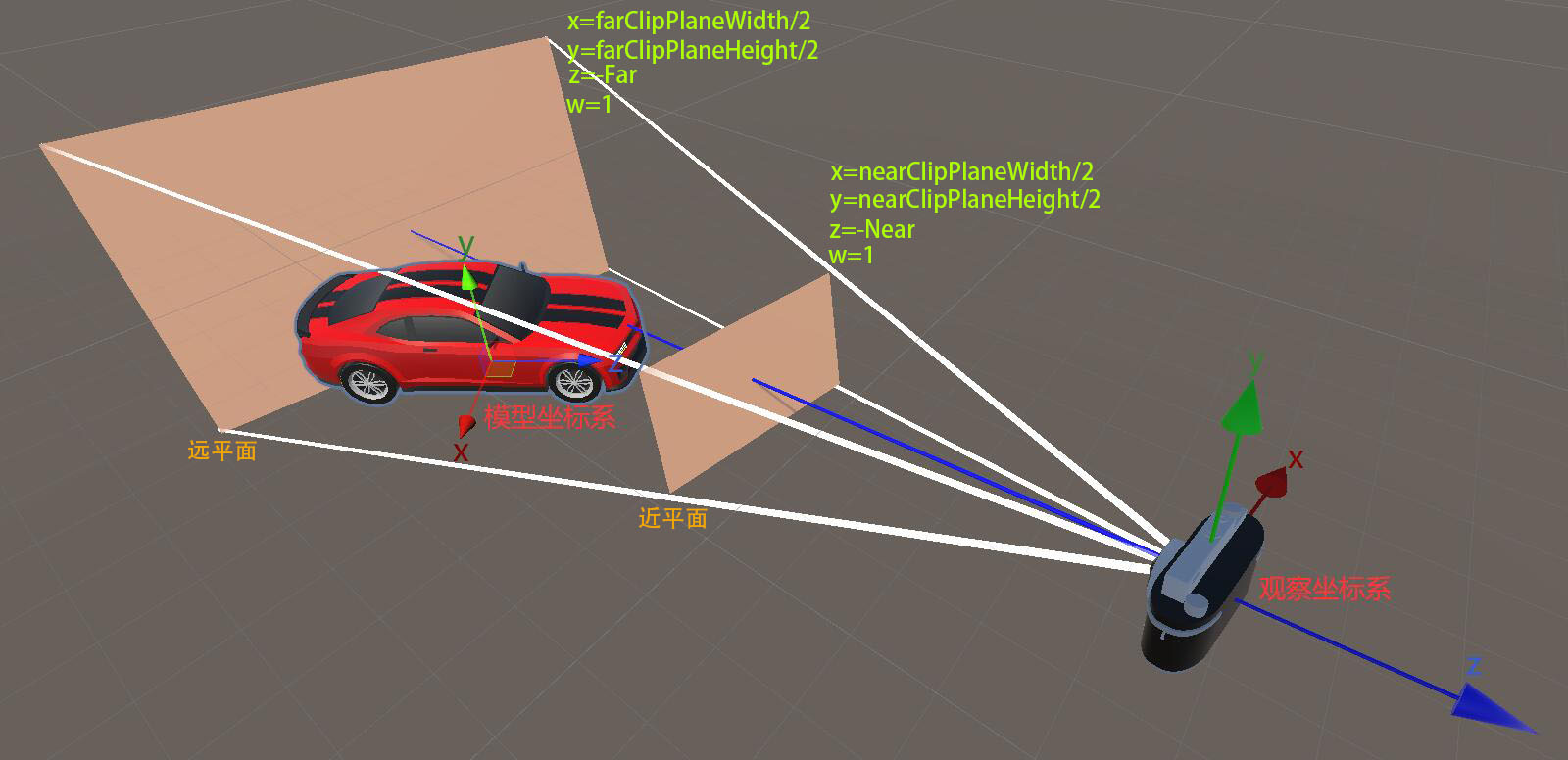
说明:近平面和远平面间棱台称为视锥体,表示可见区域范围,视锥体以外的顶点数据将被裁剪丢弃。
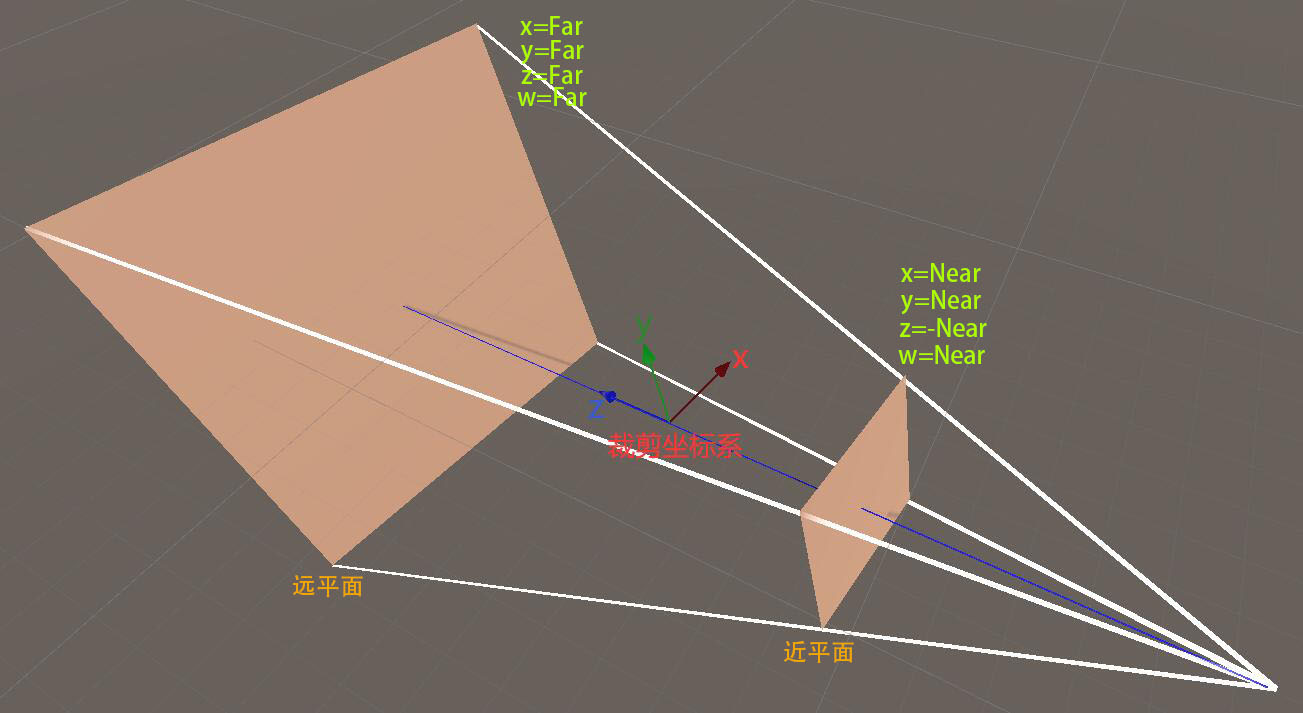
说明:裁剪空间中的点满足条件:-w < x < w,-w < y < w,-w < z < w,不满足该条件的点将被踢出掉;将满足条件的点 x、y、z 坐标除以 w(齐次除法、透视除法),就会得到归一化设备空间,该空间中的点满足条件:-1 < x < 1,-1 < y < 1,-1 < z < 1。

2 变换
2.1 模型变换
2.1.1 平移变换
对于任意点 [x, y, z, 1]',将其平移 [a, b, c, 0]',可以使用以下矩阵运算描述平移变换:

对于任意向量 [x, y, z, 0]',将其平移 [a, b, c, 0]',平移后仍然是 [x, y, z, 0],如下:

2.1.2 旋转变换
绕 x 轴旋转 α 度,对应的旋转矩阵如下:

绕 y 轴旋转 α 度,对应的旋转矩阵如下:

绕 z 轴旋转 α 度,对应的旋转矩阵如下:

当旋转角度为 [α, β, γ]' 时,对应的复合旋转矩阵为:

2.1.3 缩放变换
对于缩放系数 [kx, ky, kz]',对应的缩放矩阵如下:

当 kx = ky = kz 时,该缩放变换称为统一缩放(uniform scale),否则称为非统一缩放(nonuniform scale)。
2.1.4 对称变换
对于任意点 [x, y, z, 1]',关于点 [a, b, c, 1]' 对称的点,可以使用以下矩阵运算描述对称变换:

2.2 观察变换
将世界坐标系按照 1.2 节映射方法扩展到四维空间中,假设 x、y、z、w 轴正方向的的单位向量分别为 e1、e2、e3、e4,相机在世界坐标系下的坐标为 [a, b, c, 1]',其向右、向上、向前方向的单位向量分别为:r、u、f,则向量 r、u、-f、e4 在一组基向量 e1, e2, e3, e4 下的表示如下:(f 取负是因为观察坐标系是右手坐标系,其 z 轴的正方向与相机的前方方向相反)

由于向量 r、u、-f、e4 两两垂直,并且都是单位向量,因此由这 4 个向量组成的矩阵是正交矩阵,即 A-1 = A'。由此可知,向量 e1, e2, e3, e4 在一组基向量 r、u、-f、e4 下的表示如下:

右侧的矩阵就是坐标轴的旋转变换矩阵,另外还需要进行坐标原点的平移变换,由 1.2.1 节平移变换矩阵可知,观察变换矩阵如下:

2.3 投影变换
2.3.1 透视投影
1)透视投影相机参数
Unity 提供给用户调整透视投影矩阵的参数如下:

- Near:近平面距离相机的距离;
- Far:远平面距离相机的距离;
- Field of View:视锥体在竖直方向上的张角(以下简称 FOV);
- Viewport Rect:视口起点和宽高(左下角为原点,向右宽度增加,向上高度增加)
根据 Near、Far、FOV 的值,可以计算近平面和远平面高度分别为:

近平面和远平面的宽度由相机(或屏幕)宽高比决定,假设相机(或屏幕)宽高比为 Aspect,则近平面和远平面的宽度计算如下:

2)透视投影矩阵推导
投影的目的是:将模型顶点投影到近平面上,如下,将观察坐标系下的任意顶点 [x0, y0, z0]' 投影到近平面上,投影后的坐标为 [x1, y1, z1]’(z1 = -Near)。

根据三角形相似原理,存在以下函数关系:

为了方便后续进行屏幕映射,需要将 [x1, y1]' 进行标准化,即将 x1、y1 映射到区间 [-1, 1],当前 -nearClipPlaneWidth / 2 ≤ x1 ≤ nearClipPlaneWidth / 2,-nearClipPlaneHeight / 2 ≤ y1 ≤ nearClipPlaneHeight / 2,假设归一化后的坐标为 [x2, y2],因此存在以下关系:

将 x1、y1、nearClipPlaneWidth、nearClipPlaneHeight 使用 x0、y0、z0、Aspect、FOV 替换得:

x2、y2 已标准化,但是当前 -Far ≤ z0 ≤ -Near,我们期望将 z0 也标准化,假设标准化后的变量为 z2,则 -1 ≤ z2 ≤ 1。x2 与 x0、y2 与 y0 的关系式中,都存在 (-1 / z0),我们期望 z2 与 z0 的关系式中也存在 (-1 / z0),因此,我们假设 z2 与 z0 的关系如下:

将 [-Far, 1]'、[-Near, -1]' 代入求解得:(注意:这里不能代入 [-Far, -1]'、[-Near, 1]',因为裁剪坐标系的 z 轴和 观察坐标系的 z 轴方向相反)

将 k、b 代入 z2 与 z0 的关系式中得:

整理 x2、y2、z2 与 x0、y0、z0 的关系如下:

由于 z0 是变量,在矩阵前面乘以 (-1 / z0),使得透视变换不是线性变换,因此我们将原本的透视变换拆分为以下两步:
- 对 [x0, y0, z0, 1]' 左乘透视矩阵;
- 将第一步的结果除以 (-z0)。
为保证透视变换的线性性质,我们将第二步变换移到屏幕映射中处理,并将其定义为齐次除法(或透视除法),而将第一步变换作为透视变换,其对应的矩阵如下:

说明:P(4, 3) 定义为 -1 是为了将观察坐标系中顶点的深度信息 (-z) 传递给下一步(齐次除法或透视除法)处理(用 w 存储,即 w = -z),避免深度信息丢失。经透视变换后,顶点坐标的 x、y、z 分量将约束在 [z, -z] 区间,即 [-w, w],在该区间外的顶点将被丢弃。
经过透视变换后,观察空间和裁剪空间视锥体的对比如下:

2.3.2 正交投影
1)正交投影相机参数
Unity 提供给用户调整正交投影矩阵的参数如下:

- Size:视锥体在竖直方向上的高度的一半;
- Near:近平面距离相机的距离;
- Far:远平面距离相机的距离;
- Viewport Rect:视口起点和宽高(左下角为原点,向右宽度增加,向上高度增加)
2)正交投影矩阵推导
投影的目的是:将模型顶点投影到近平面上,如下,将观察坐标系下的任意顶点 [x0, y0, z0]' 投影到近平面上,投影后的坐标为 [x0, y0, -Near]‘。

为了方便后续进行屏幕映射,需要将 [x0, y0, z0]' 进行标准化,即将 x0、y0、z0 映射到区间 [-1, 1],当前 -Aspect · Size ≤ x1 ≤ Aspect · Size,-Size ≤ y1 ≤ Size,-Far ≤ z0 ≤ -Near,假设归一化后的坐标为 [x1, y1, z1]',因此存在以下关系:

说明:正交投影变换后,w 分量的值仍然是 1,从而保证 [x1, y1, z1]' 经齐次除法(除以 w1)后,仍然是标准化坐标(即值域为 [-1, 1]),这样做的好处是:下游不用区分上游传递过来的数据是透视投影还是正交投影处理后的数据。经正交投影变换后,顶点坐标的 x、y、z 分量将约束在 [-1, 1] 区间,在该区间外的顶点将被丢弃。
经过正交投影变换后,观察空间和裁剪空间视锥体的对比如下:

2.4 齐次除法和屏幕映射
2.4.1 齐次除法
经透视投影或正交投影后,将坐标 [x, y, z, w] 中的 x、y、z 分量都除以其 w 分量的值,使得 x、y、z 都约束在 [-1, 1] 区间,该过程称为齐次除法(或透视除法),得到的坐标称为归一化的设备坐标(NDC)。

2.4.2 屏幕映射
经齐次除法后,将坐标的 x、y 值映射到屏幕像素位置,该过程称为屏幕映射。映射前 x、y 的值域为 [-1, 1],映射后 x 的值域为 [0, pixelWidth],y 的值域为 [0, pixelHeight],屏幕左下角坐标为 [0, 0],右上角坐标为 [pixelWidth, pixelHeight]。屏幕映射公式如下:

2.5 法线变换
假设模型变换为 M,模型空间中某点法线向量为 n,如果模型变换中包含非统一缩放(即 x、y、z 的缩放系数不全相等), 此时若按照 M · n 计算法线的世界坐标,就会出现变换后的法线与切面不垂直,如下图。

法线由切线计算而来,在模型空间中 A 点的切线向量为 v1,法线向量为 n1,经过模型变换(矩阵 M)后,切线向量为 v2,法线向量为 n2,假设法线向量的变换矩阵为 G,因此存在以下关系:

Unity 中线性变换主要有平移、旋转、缩放,由于向量不受平移变换影响,因此,对于法线向量而言,只受旋转和缩放影响。
- 当 M 只包含旋转变换时,M 是正交矩阵,,因此 G = M;
- 当 M 只包含统一缩放变换时,M = k·E,因此 G = 1/k·E = 1/(k^2)·M,由于法线向量只需要方向,后面会进行归一化,因此可以简写 G = M;
- 当 M 只包含旋转变换和统一缩放变换时,G = 1/(k^2)·M,由于法线向量只需要方向,后面会进行归一化,因此可以简写 G = M;
Unity 中法线变换源码如下:
UnityCG.cginc
// 局部空间->世界空间
float3 UnityObjectToWorldNormal(float3 norm) {
#ifdef UNITY_ASSUME_UNIFORM_SCALING // 统一缩放(x、y、z分量缩放系数一致)return UnityObjectToWorldDir(norm); // normalize(mul((float3x3)unity_ObjectToWorld, norm))
#elsereturn normalize(mul(norm, (float3x3)unity_WorldToObject)); // mul(IT_M, norm) => mul(norm, I_M)
#endif
}相关文章:

【Unity3D】空间和变换
1 空间 1.1 左右手坐标系及其法则 1.1.1 左右手坐标系 左手坐标系与右手坐标系Unity 局部空间、世界空间、裁剪空间、屏幕空间都采用左手坐标系,只有观察空间采用右手坐标系。 左右手坐标系除了坐标系朝向(旋向性)不同,还存在以…...

脑洞|ChatGPT加持下,ChatOps将如何革新团队协作与运维管理?
要说近期科技圈 “顶流”,非 ChatGPT 莫属。 比起目前常见的语音助手与聊天 bot,这位机器人显得更有 “人味儿”,不仅能模拟人类的语气,跟你聊得有来有回,还能写剧本、编音乐、写代码。 说到聊天工具,就让…...
)
华为OD机试真题Python实现【找数字】真题+解题思路+代码(20222023)
找数字 题目 给一个二维数组nums,对于每一个元素num[i],找出距离最近的且值相等的元素,输出横纵坐标差值的绝对值之和,如果没有等值元素,则输出-1。 例如: 输入数组nums为 0 3 5 4 2 2 5 7 8 3 2 5 4 2 4对于 num[0][0] = 0,不存在相等的值。 对于 num[0][1] = 3,存…...
【Database-01】达梦数据库Docker版下载安装
1、前往达梦数据库官网下载 https://www.dameng.com/1.1、选择数据库 - 数据库产品系 1.2、选择 达梦数据库管理系统(DM8) 1.3、点击试用下载 1.4、注册达梦账户 1.5、选择DM8 Docker镜像 https://www.dameng.com/list_103.html1.6、或者使用以下网址也…...
Allegro如何打开格点显示效果操作指导
Allegro如何打开格点显示效果操作指导 Allegro可以设置格点显示效果,以格点来判定走线等等是否都处于格点上,如下图 如何打开格点显示效果,具体操作如下 点击Setup点击Grids...
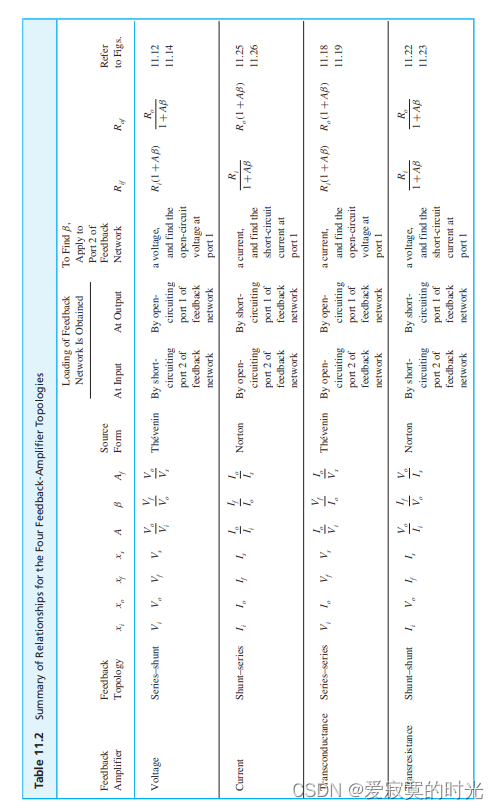
电子技术——反馈放大器的分析方法总结
电子技术——反馈放大器的分析方法总结 第一种也是最简单的估算方法,直接拿出反馈网络,计算 β\betaβ 则假设在 AβA\betaAβ 无限大的情况下有 Af≃1/βA_f \simeq 1/\betaAf≃1/β 。开环法。比第一种方法更能精确的估计 AAA 和 β\betaβ 的值。系…...
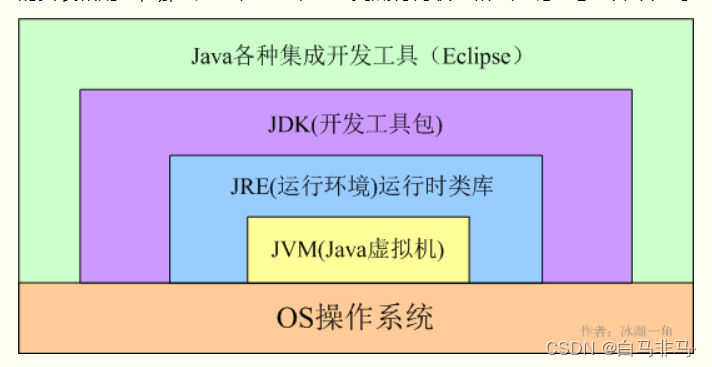
微服务系统启动,环境从0开始的搭建过程
1. JDK的下载安装(傻瓜式) 安装过程傻瓜式,直接一步到位。我安装的版本为:jdk-17_windows-x64_bin 2. 集成开发工具的下载安装:IDEA(傻瓜式) ideaIU-2021.2.1 网上资源很多,自己找…...
手工测试1年经验面试,张口要13K,我真是服了····
由于朋友临时有事, 所以今天我代替朋友进行一次面试,他需要应聘一个测试工程师, 我以很认真负责的态度完成这个过程, 大概近30分钟。 主要是技术面试, 在近30分钟内, 我与被面试者是以交流学习的方式进行的…...
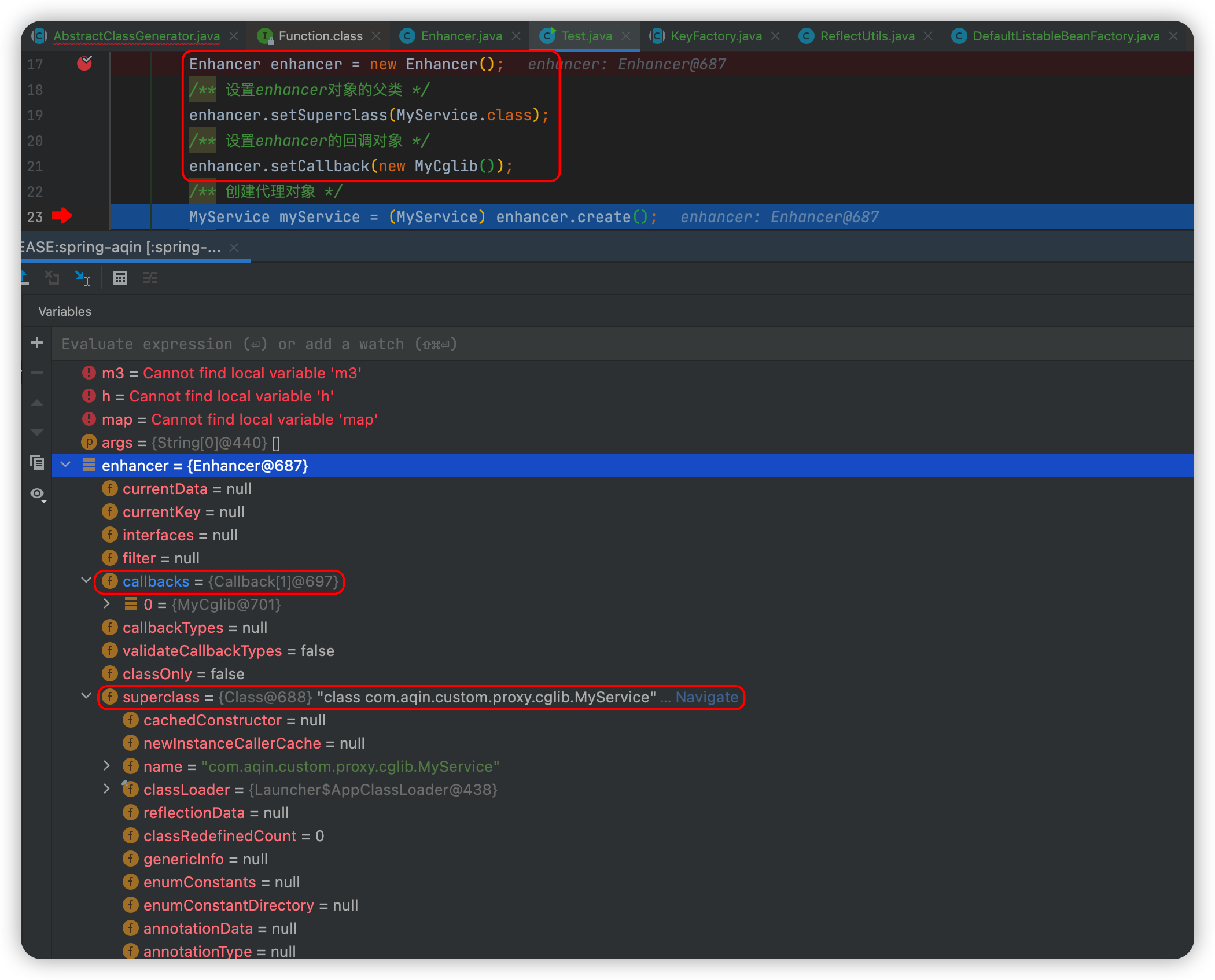
【保姆级】手把手捋动态代理流程(JDK+Cglib超详细源码分析)
简介动态代理,通俗点说就是:无需声明式的创建java代理类,而是在运行过程中生成"虚拟"的代理类,被ClassLoader加载。 从而避免了静态代理那样需要声明大量的代理类。上面的简介中提到了两个关键的名词:“静态…...

Appium自动化测试 Inspector定位Webview/H5页面元素
目录操作步骤Python操作该混合App代码Appium在操作混合App或Android App的H5页面时, 常常需要定位H5页面中的元素, 传统方式是 FQ 使用Chrome://inspect来定位元素, 环境准备相当繁琐, 不仅需要想办法FQ, 而且还需要Android设备安装Google框架以及手机版Chrome浏览器以及相应的…...

数组求和方法总结,学点干货
1.循环 (新手用) 1.1 普通for 循环 简单质朴 const arr [1, 2, 3, 4, 5];let sum 0;for (let i 0; i < arr.length; i) {sum arr[i];}1.2 for in 循环 与普通for循环大同小异 const arr [1, 2, 3, 4, 5];let sum 0;for (let i in arr) {sum …...
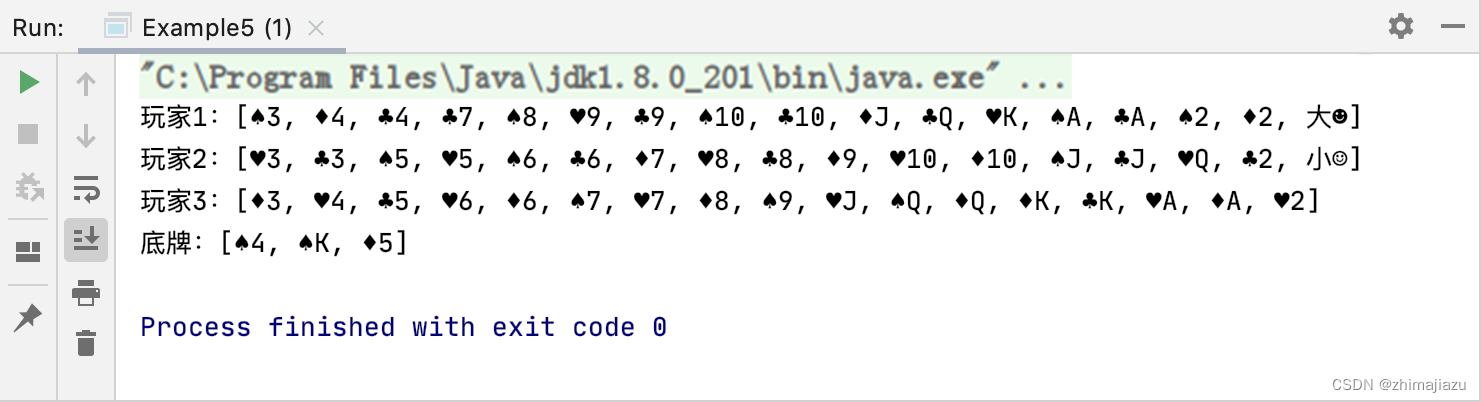
斗地主洗牌发牌-课后程序(JAVA基础案例教程-黑马程序员编著-第六章-课后作业)
【案例6-4】 斗地主洗牌发牌 【案例介绍】 1.任务描述 扑克牌游戏“斗地主”,相信许多人都会玩,本案例要求编写一个斗地主的洗牌发牌程序,要求按照斗地主的规则完成洗牌发牌的过程。一副扑克总共有54张牌,牌面由花色和数字组成…...

基于antd封装的二次业务筛选组件-table-filter
文档地址:https://flowerofsummer.github.io/components/ 业务筛选组件 支持各种类型的高级搜索组件 基础用法 组件响应式布局,默认显示两行,可以通过 maxLineCount 配置最多显示行数每行个数: 如果含有 time-range࿰…...
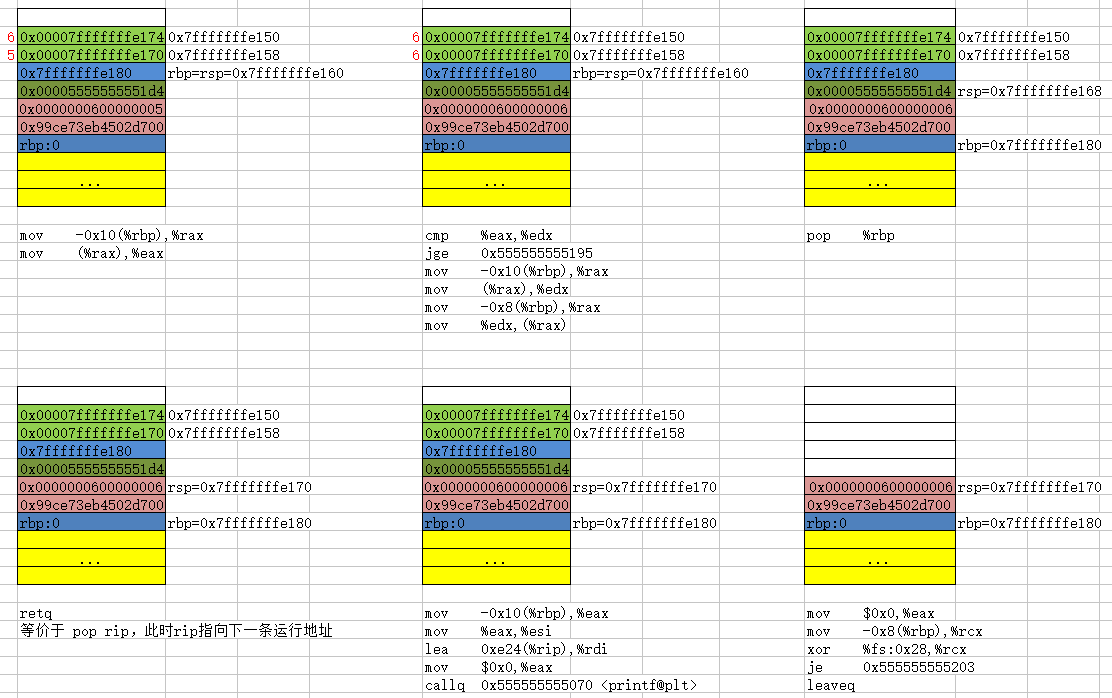
逆向-还原代码之max 再画堆栈图 (Interl 64)
// source code #include <stdio.h> void max(int * a, int * b) { if (*a < *b) *a *b; } int main() { int a 5, b 6; max(&a, &b); printf("a, b max %d\n", a); return 0; } // 再画堆栈图 下周一(2.27…...
GitHub标星30K+的Java面试八股文长啥样?
2023年的互联网行业竞争越来越严峻,面试也是越来越难,一直以来我都想整理一套完美的面试宝典,奈何难抽出时间,这套1000道的Java面试手册我整理了整整1个月,上传到Git上目前star数达到了30K 一、32 道 MySQL 面试题 1&…...
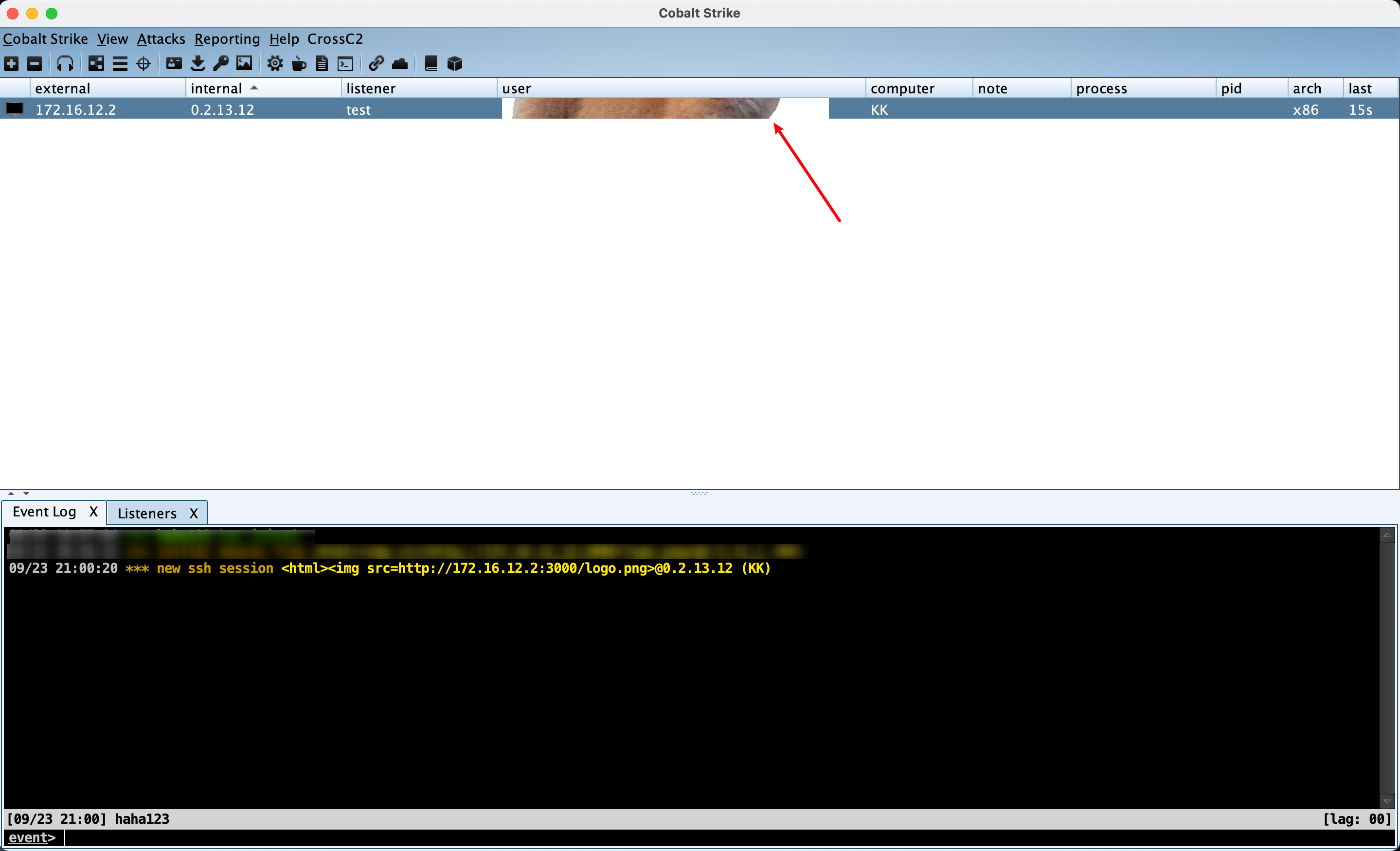
CVE-2022-39197 POC(CobaltStrike XSS <=4.7)漏洞复现
漏洞说明 根据9.20日CobaltStrike官方发布的最新4.7.1版本的更新日志中介绍,<4.7的teamserver版本存在XSS漏洞,从而可以造成RCE远程代码执行 一位名为“Beichendream”的独立研究人员联系我们,告知我们他们在团队服务器中发现的一个 XSS …...
我们来说说蹿红的AIGC到底是什么?ChatGPT又是什么?
近期,人工智能(AI)领域动作频频,OPENAI公司Chat GPT的出现,标志着人工智能的研究与应用已经进入了一个崭新的发展阶段,国内腾讯、阿里巴巴、百度、易网、国外微软、谷歌、苹果、IBM、Amazon,等互…...

新手如何从零开始搭建配置Windows云服务器?
新手如何从零开始搭建配置Windows云服务器?本文是搭建 Windows 云服务器入门教程,主要介绍如何从零开始,以最简单的方式搭建和配置你的Windows 云服务器。如果您之前没有搭建云服务器的经验,建议您按照本文介绍的方式来购买和配置…...
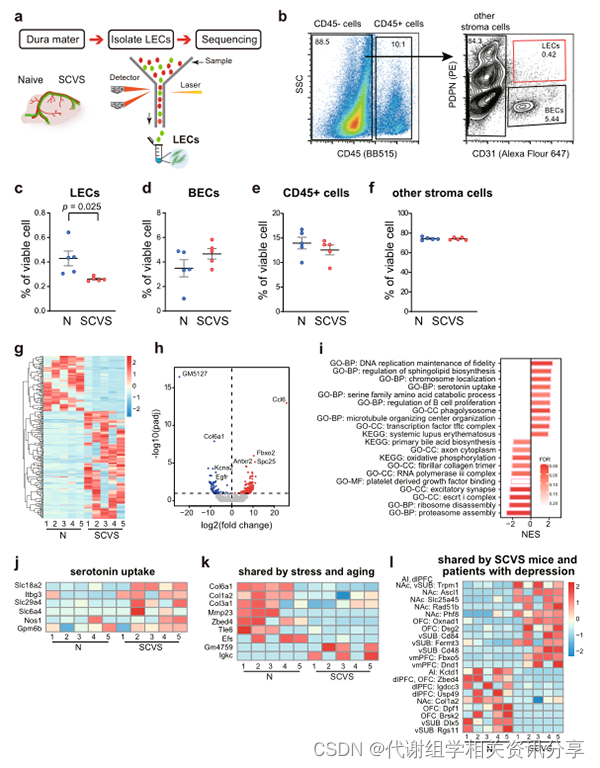
百趣代谢组学-抑郁症居然“男女有别”,脑膜淋巴管起关键作用!
文章标题:A functional role of meningeal lymphatics in sex difference of stress susceptibility in mice 发表期刊:Nature Communications 影响因子:17.694 发表时间:2022年8月 作者单位:中山大学中山医学院 …...

C语言实现用堆解决 TOP-K 问题
目录 TopK函数实现 如何测试 完整源码 生活中我们经常能见到TopK问题,例如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。 所以,TopK问题即求出一组数据中前K个最大或最小的元素,一般情况下,数据量都…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
