Python每日一练(20230223)

目录
1. 合并区间
2. 单词接龙
3. N皇后
附录:回溯算法
基本思想
一般步骤
1. 合并区间
难度:★★
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
代码:
class Interval(object):def __init__(self, s=0, e=0):self.start = sself.end = eclass Solution(object):def list2interval(self, list_interval):ret = []for i in list_interval:interval = Interval(i[0], i[1])ret.append(interval)return retdef interval2list(self, interval):ret = []x = [0,0]for i in interval:x[0] = i.startx[1] = i.endret.append(x)x = [0,0]return retdef merge(self, intervals):""":type intervals: List[Interval]:rtype: List[Interval]"""if intervals is None:returnls = len(intervals)if ls <= 1:return intervalsintervals = self.list2interval(intervals) intervals.sort(key=lambda x: x.start)pos = 0while pos < len(intervals) - 1:if intervals[pos].end >= intervals[pos + 1].start:next = intervals.pop(pos + 1)if next.end > intervals[pos].end:intervals[pos].end = next.endelse:pos += 1intervals = self.interval2list(intervals)return intervalsif __name__ == '__main__':s = Solution()print(s.merge(intervals = [[1,4],[4,5]]))print(s.merge(intervals = [[1,3],[2,6],[8,10],[15,18]]))
输出:
[[1, 5]]
[[1, 6], [8, 10], [15, 18]]
2. 单词接龙
难度:★★★ (BFS)
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是
beginWord。 - 序列中最后一个单词是
endWord。 - 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典
wordList中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] 输出:5 解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] 输出:0 解释:endWord "cog" 不在字典中,所以无法进行转换。
提示:
1 <= beginWord.length <= 10endWord.length == beginWord.length1 <= wordList.length <= 5000wordList[i].length == beginWord.lengthbeginWord、endWord和wordList[i]由小写英文字母组成beginWord != endWordwordList中的所有字符串 互不相同
代码:
class Solution:def ladderLength(self, beginWord, endWord, wordList):""":type beginWord: str:type endWord: str:type wordList: List[str]:rtype: int"""if endWord not in wordList:return 0if beginWord in wordList:wordList.remove(beginWord)wordDict = dict()for word in wordList:for i in range(len(word)):tmp = word[:i] + "_" + word[i + 1 :]wordDict[tmp] = wordDict.get(tmp, []) + [word]stack, visited = [(beginWord, 1)], set()while stack:word, step = stack.pop(0)if word not in visited:visited.add(word)if word == endWord:return stepfor i in range(len(word)):tmp = word[:i] + "_" + word[i + 1 :]neigh_words = wordDict.get(tmp, [])for neigh in neigh_words:if neigh not in visited:stack.append((neigh, step + 1))return 0if __name__ == '__main__':s = Solution()beginWord = "hit"endWord = "cog"wordList = ["hot","dot","dog","lot","log","cog"]print(s.ladderLength(beginWord, endWord, wordList))wordList = ["hot","dot","dog","lot","log"]print(s.ladderLength(beginWord, endWord, wordList))
输出:
5
0
3. N皇后
难度:★★★ (回溯)
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
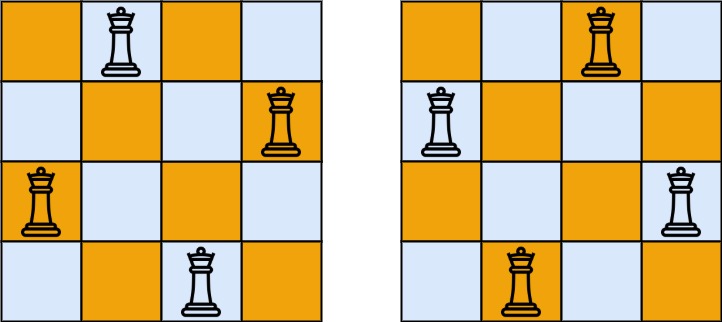
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
代码:
class Solution(object):def solveNQueens(self, n):if n == 0:return 0res = []board = [['.'] * n for t in range(n)]self.do_solveNQueens(res, board, n)return resdef do_solveNQueens(self, res, board, num):if num == 0:res.append([''.join(t) for t in board])returnls = len(board)pos = ls - numcheck = [True] * lsfor i in range(pos):for j in range(ls):if board[i][j] == 'Q':check[j] = Falsestep = pos - iif j + step < ls:check[j + step] = Falseif j - step >= 0:check[j - step] = Falsebreakfor j in range(ls):if check[j]:board[pos][j] = 'Q'self.do_solveNQueens(res, board, num - 1)board[pos][j] = '.'if __name__ == '__main__':s = Solution()print(s.solveNQueens(4))print(s.solveNQueens(1))
输出:
[['.Q..', '...Q', 'Q...', '..Q.'], ['..Q.', 'Q...', '...Q', '.Q..']]
[['Q']]
附录:回溯算法
回溯算法也叫试探法,是一种系统地搜索问题的解题方法。实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
基本思想
从一条路往前走,能进则进,不能进则退回来,换一条路再试。八皇后问题就是回溯算法的典型,第一步按照顺序放一个皇后,然后第二步符合要求放第2个皇后,如果没有位置符合要求,那么就要改变第一个皇后的位置,重新放第2个皇后的位置,直到找到符合条件的位置就可以了。回溯在迷宫搜索中使用很常见,就是这条路走不通,然后返回前一个路口,继续下一条路。回溯算法说白了就是穷举法。不过回溯算法使用剪枝函数,剪去一些不可能到达 最终状态(即答案状态)的节点,从而减少状态空间树节点的生成。回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯。否则,进入该子树,继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时,只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题。
一般步骤
1、针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
2、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间。
3、以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
确定了解空间的组织结构后,回溯法就从开始结点(根结点)出发,以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点,并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已没有活结点时为止。
相关文章:

Python每日一练(20230223)
目录 1. 合并区间 2. 单词接龙 3. N皇后 附录:回溯算法 基本思想 一般步骤 1. 合并区间 难度:★★ 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回…...
Flask----------第一个flask项目,debug、host、port的配置
目录 1.flask 1.简介 2.flask框架的优势 2.第一个flask项目 3.debug 开启debug方法 1.专业版 2.社区版 4.修改host 5. 修改port端口 1.flask 1.简介 Flask是一个基于Python开发并且依赖jinja2模板和Werkzeug WSGI服务的一个微型框架,对于Werkzeug本质是So…...
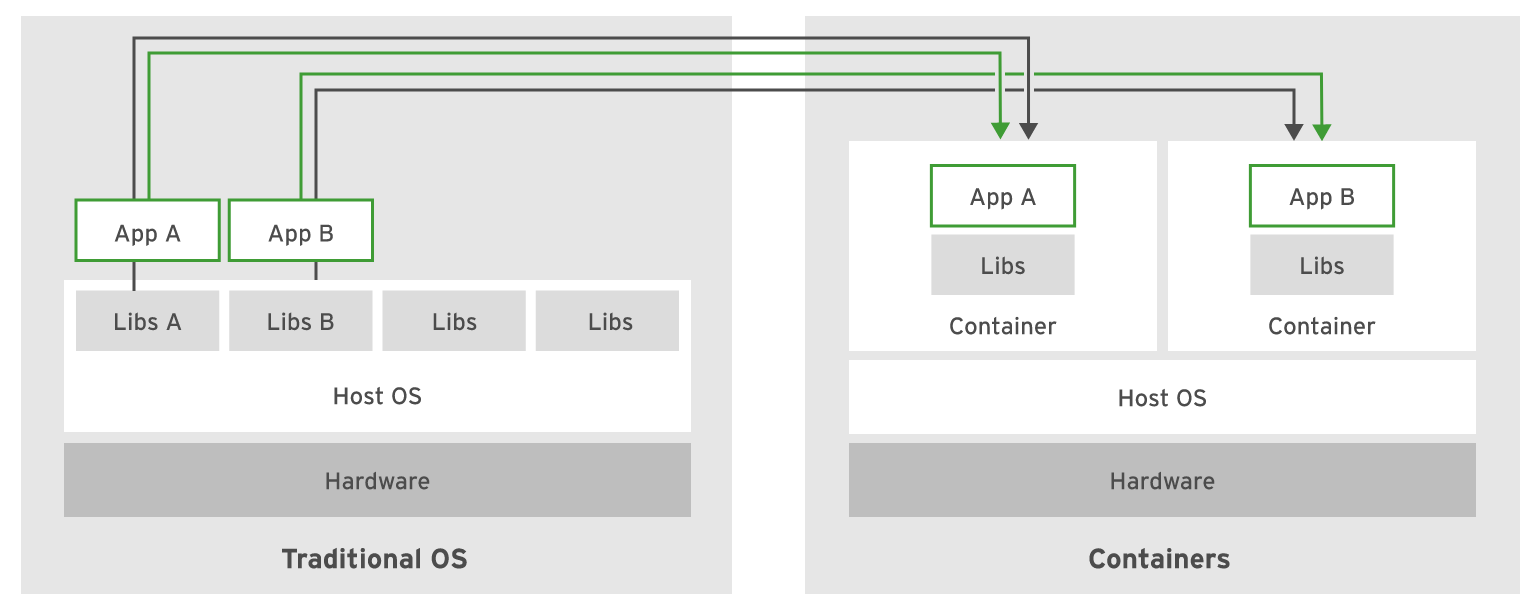
容器技术概述
容器技术概述 软件应用程序通常依赖于运行时环境提供的其他库、配置文件或服务。软件应用程序的传统运行环境是物理主机或虚拟机,应用程序依赖项作为主机的一部分安装。 例如,考虑一个 Python 应用程序,它需要访问实现 TLS 协议的公共共享库…...

「SAP」ABAP模块学习需要了解什么?快收下这份ABAP技术栈指南【附技能树】
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计专业大二本科在读,阿里云社区专家博主,华为云社区云享专家,CSDN SAP应用技术领域新兴创作者。 在学习工…...

【python 基础篇 九】python的常用数据类型操作-------时间日历
目录1.python时间操作1.1 time模块1.2 calendar模块1.3 datetime模块1.python时间操作 python程序能用很多方式处理日期和时间,转换日期格式也是一个常见功能。 1.1 time模块 提供了处理时间和表示之间转换的功能 获取当前时间戳 概念:从0时区的1…...
)
华为OD机试真题Python实现【相同字符连续出现的最大次数】真题+解题思路+代码(20222023)
相同字符连续出现的最大次数 题目 输入一串字符串 字符串长度不超过100 查找字符串中相同字符连续出现的最大次数 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 输入只有一行,包含一个长度不超过100的字符串 输出描述 输出只…...

【Unity3D】空间和变换
1 空间 1.1 左右手坐标系及其法则 1.1.1 左右手坐标系 左手坐标系与右手坐标系Unity 局部空间、世界空间、裁剪空间、屏幕空间都采用左手坐标系,只有观察空间采用右手坐标系。 左右手坐标系除了坐标系朝向(旋向性)不同,还存在以…...

脑洞|ChatGPT加持下,ChatOps将如何革新团队协作与运维管理?
要说近期科技圈 “顶流”,非 ChatGPT 莫属。 比起目前常见的语音助手与聊天 bot,这位机器人显得更有 “人味儿”,不仅能模拟人类的语气,跟你聊得有来有回,还能写剧本、编音乐、写代码。 说到聊天工具,就让…...
)
华为OD机试真题Python实现【找数字】真题+解题思路+代码(20222023)
找数字 题目 给一个二维数组nums,对于每一个元素num[i],找出距离最近的且值相等的元素,输出横纵坐标差值的绝对值之和,如果没有等值元素,则输出-1。 例如: 输入数组nums为 0 3 5 4 2 2 5 7 8 3 2 5 4 2 4对于 num[0][0] = 0,不存在相等的值。 对于 num[0][1] = 3,存…...
【Database-01】达梦数据库Docker版下载安装
1、前往达梦数据库官网下载 https://www.dameng.com/1.1、选择数据库 - 数据库产品系 1.2、选择 达梦数据库管理系统(DM8) 1.3、点击试用下载 1.4、注册达梦账户 1.5、选择DM8 Docker镜像 https://www.dameng.com/list_103.html1.6、或者使用以下网址也…...
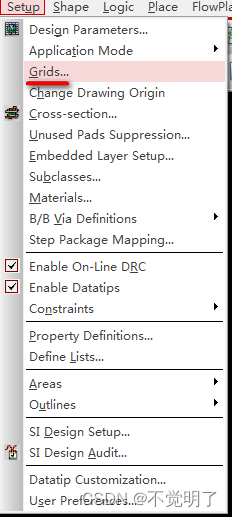
Allegro如何打开格点显示效果操作指导
Allegro如何打开格点显示效果操作指导 Allegro可以设置格点显示效果,以格点来判定走线等等是否都处于格点上,如下图 如何打开格点显示效果,具体操作如下 点击Setup点击Grids...
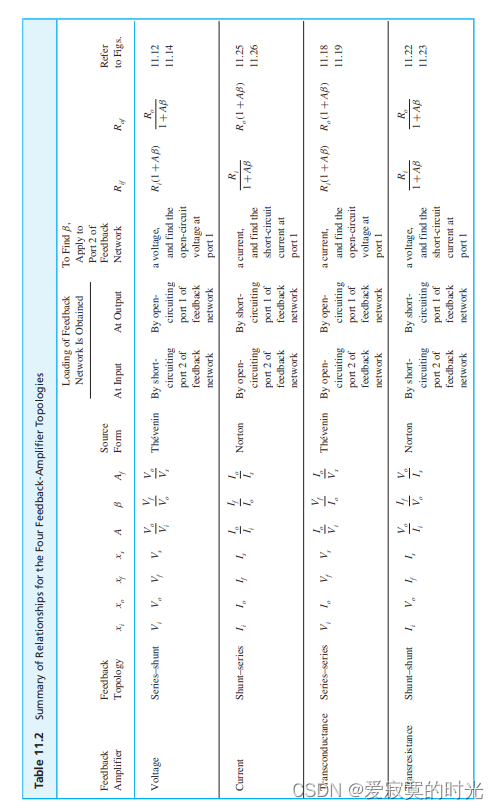
电子技术——反馈放大器的分析方法总结
电子技术——反馈放大器的分析方法总结 第一种也是最简单的估算方法,直接拿出反馈网络,计算 β\betaβ 则假设在 AβA\betaAβ 无限大的情况下有 Af≃1/βA_f \simeq 1/\betaAf≃1/β 。开环法。比第一种方法更能精确的估计 AAA 和 β\betaβ 的值。系…...
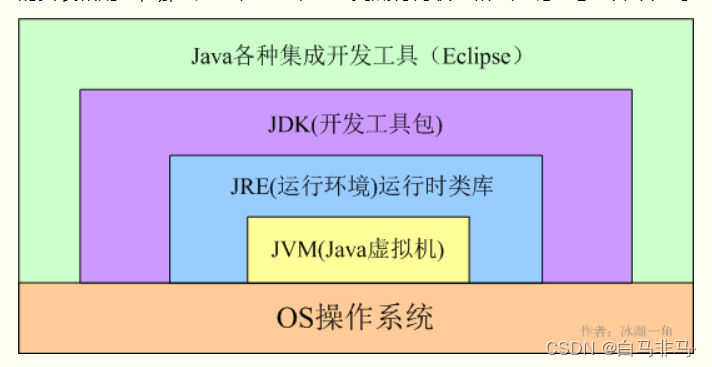
微服务系统启动,环境从0开始的搭建过程
1. JDK的下载安装(傻瓜式) 安装过程傻瓜式,直接一步到位。我安装的版本为:jdk-17_windows-x64_bin 2. 集成开发工具的下载安装:IDEA(傻瓜式) ideaIU-2021.2.1 网上资源很多,自己找…...
手工测试1年经验面试,张口要13K,我真是服了····
由于朋友临时有事, 所以今天我代替朋友进行一次面试,他需要应聘一个测试工程师, 我以很认真负责的态度完成这个过程, 大概近30分钟。 主要是技术面试, 在近30分钟内, 我与被面试者是以交流学习的方式进行的…...
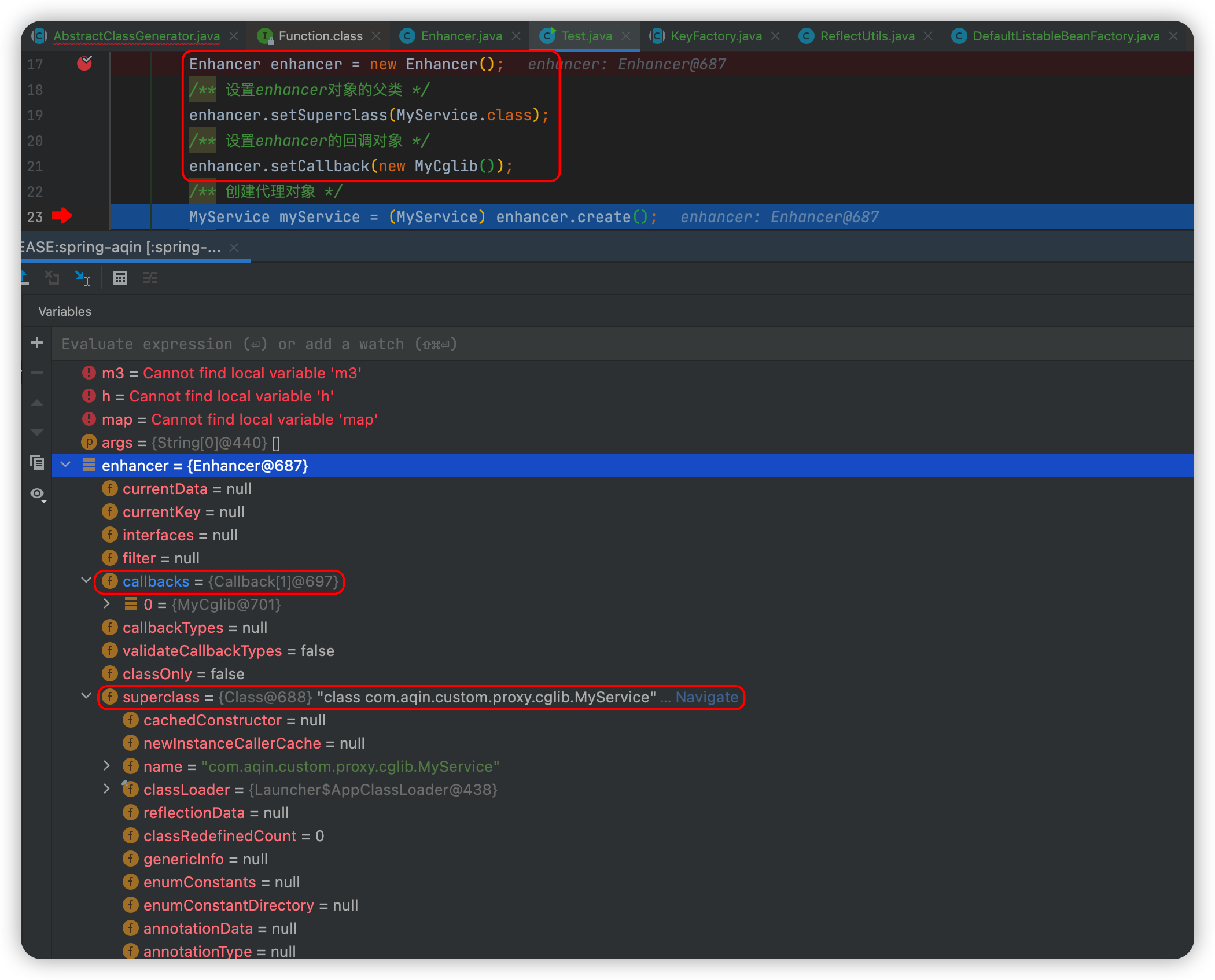
【保姆级】手把手捋动态代理流程(JDK+Cglib超详细源码分析)
简介动态代理,通俗点说就是:无需声明式的创建java代理类,而是在运行过程中生成"虚拟"的代理类,被ClassLoader加载。 从而避免了静态代理那样需要声明大量的代理类。上面的简介中提到了两个关键的名词:“静态…...

Appium自动化测试 Inspector定位Webview/H5页面元素
目录操作步骤Python操作该混合App代码Appium在操作混合App或Android App的H5页面时, 常常需要定位H5页面中的元素, 传统方式是 FQ 使用Chrome://inspect来定位元素, 环境准备相当繁琐, 不仅需要想办法FQ, 而且还需要Android设备安装Google框架以及手机版Chrome浏览器以及相应的…...

数组求和方法总结,学点干货
1.循环 (新手用) 1.1 普通for 循环 简单质朴 const arr [1, 2, 3, 4, 5];let sum 0;for (let i 0; i < arr.length; i) {sum arr[i];}1.2 for in 循环 与普通for循环大同小异 const arr [1, 2, 3, 4, 5];let sum 0;for (let i in arr) {sum …...
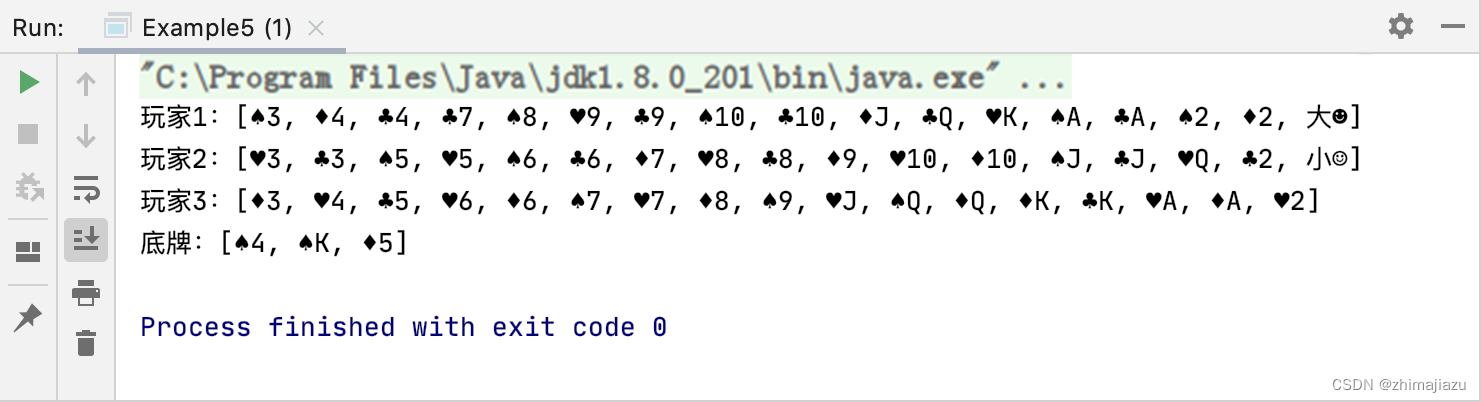
斗地主洗牌发牌-课后程序(JAVA基础案例教程-黑马程序员编著-第六章-课后作业)
【案例6-4】 斗地主洗牌发牌 【案例介绍】 1.任务描述 扑克牌游戏“斗地主”,相信许多人都会玩,本案例要求编写一个斗地主的洗牌发牌程序,要求按照斗地主的规则完成洗牌发牌的过程。一副扑克总共有54张牌,牌面由花色和数字组成…...

基于antd封装的二次业务筛选组件-table-filter
文档地址:https://flowerofsummer.github.io/components/ 业务筛选组件 支持各种类型的高级搜索组件 基础用法 组件响应式布局,默认显示两行,可以通过 maxLineCount 配置最多显示行数每行个数: 如果含有 time-range࿰…...
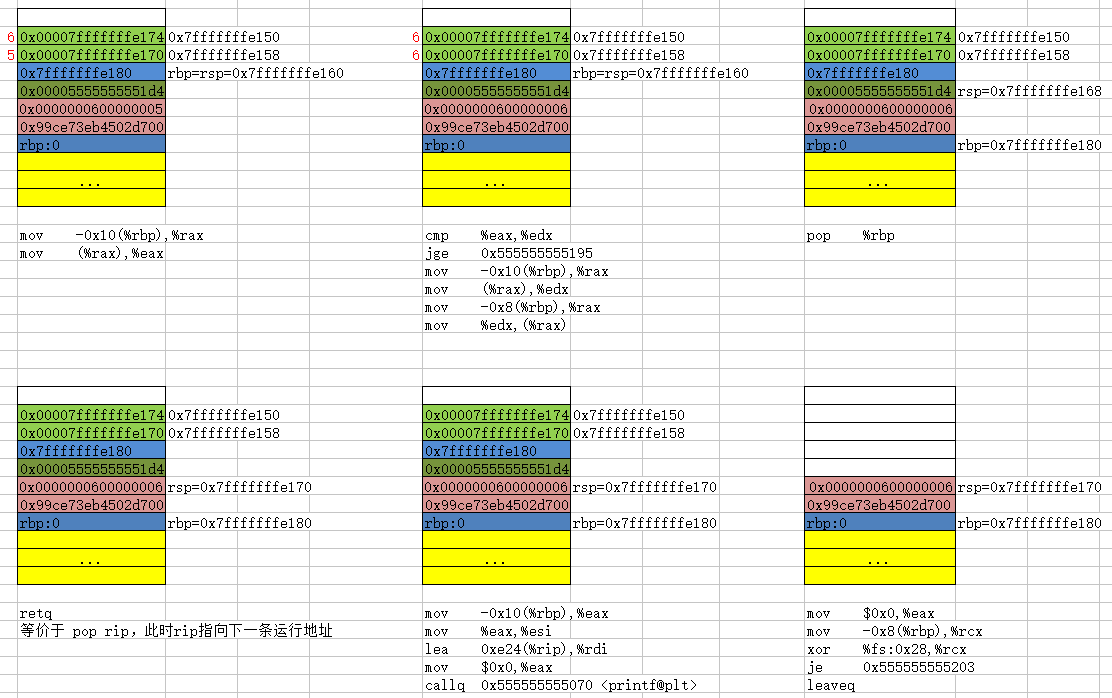
逆向-还原代码之max 再画堆栈图 (Interl 64)
// source code #include <stdio.h> void max(int * a, int * b) { if (*a < *b) *a *b; } int main() { int a 5, b 6; max(&a, &b); printf("a, b max %d\n", a); return 0; } // 再画堆栈图 下周一(2.27…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
