【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 一、二叉树的深度优先遍历
- 🌺1.前序遍历
- (1)`先序遍历`的过程:
- (2)流程图:
- (3)代码:
- (4)测试结果:
- 🌼2.中序遍历
- (1)`中序遍历`的过程:
- (2)代码:
- (3)测试结果:
- 🌻3.后序遍历
- (1) `后序遍历`的过程:
- (2)代码:
- (3)测试结果:
- 二、【广度优先】层序遍历
- 1.思路及过程:
- 2.代码
- 3.测试结果
一、二叉树的深度优先遍历
🌺1.前序遍历
(1)先序遍历的过程:
1.先访问当前节点(即根节点)
2.遍历当前节点的左节点,再同样遍历左子树中的节点
3.遍历完当前节点的左子树后,再去遍历当前节点的右子树,再遍历右子树中的节点
总结:先访问根节点,然后遍历左子树,最后遍历右子树;即根左右
(2)流程图:
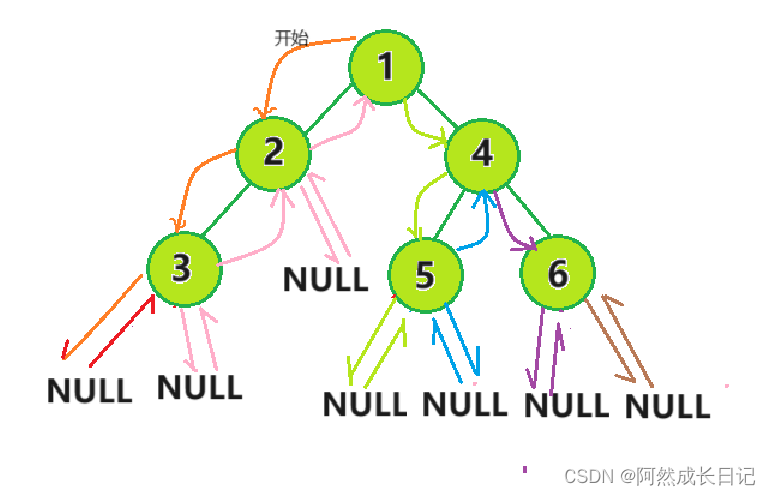
(3)代码:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}(4)测试结果:
1->2->3->NULL->NULL->NULL->4->5->NULL->NULL->6->NULL->NULL
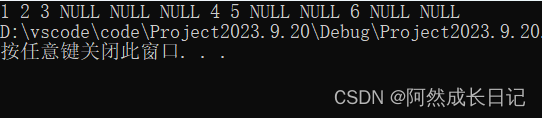
🌼2.中序遍历
(1)中序遍历的过程:
1.先进入当前节点的左子树,以同样的步骤遍历左子树的节点
2.访问当前节点
3.最后进入到当前节点的右子树,以同样的步骤遍历右子树中的节点
总结: 先遍历左子树,再访问根节点,最后遍历右子树,即 左根右
(2)代码:
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePrevOrder(root->_left);printf("%d ", root->_data);BinaryTreePrevOrder(root->_right);
}
(3)测试结果:
NULL->3->NULL->2->NULL->1->NULL->5->4->NULL->6->NULL
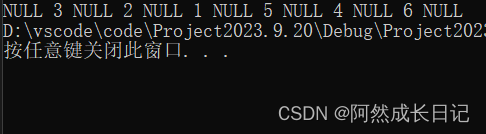
🌻3.后序遍历
(1) 后序遍历的过程:
1.先进入当前节点的左子树,以同样的步骤遍历左子树中的节点
2.再进入当前节点的右子树,以同样的步骤去遍历右子树中的节点
3.最后遍历此左子树和右子树的父亲节点,也就是该节点
总结:先遍历左子树,再遍历右子树,最后访问根节点,即左右根
(2)代码:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%d ", root->_data);
}(3)测试结果:
NULL->NULL->3->NULL->2->NULL->NULL->5->NULL->NULL->6->4->1
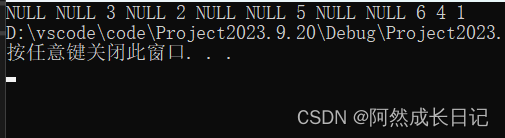
二、【广度优先】层序遍历
1.思路及过程:
构建一颗二叉树
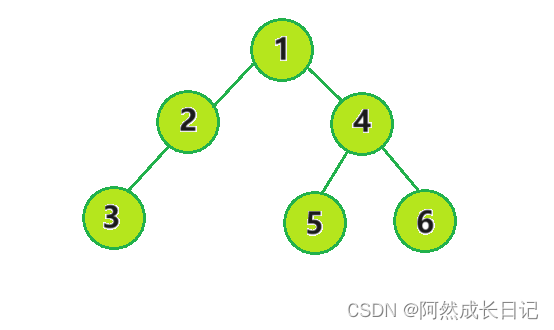
1.将root节点1放入队列。
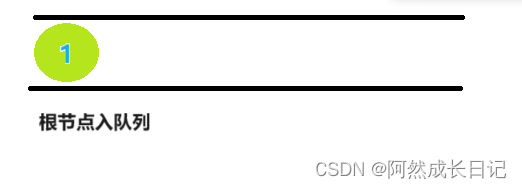
2.取队列首元素1,并将节点1的左右孩子入队
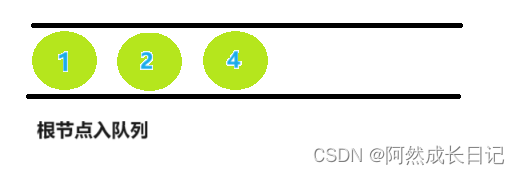
3.队首元素出队列
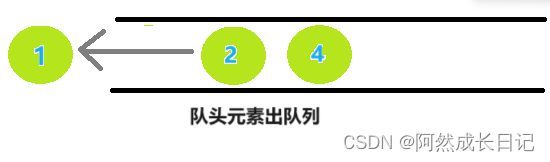
4.取队列首元素2,并将节点2的左右孩子入队,由于只有左孩子,所以只用入队一个元素。
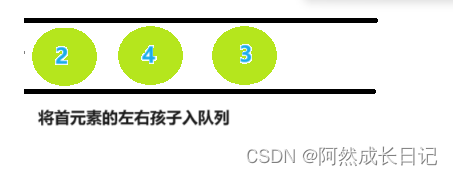
5.队首元素出队列

6.取队列首元素4,并将节点4的左右孩子入队。
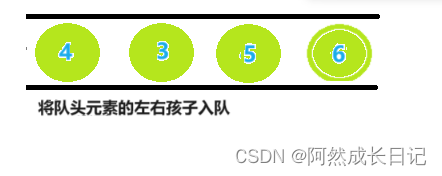
7.队首元素出队列
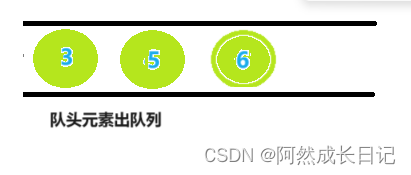
8.取队列首元素3,并将节点3的左右孩子入队。但是,元素3左右孩子为NULL,因此不用入队。直接执行出队列操作。

9.取队列首元素5,并将节点5的左右孩子入队。但是,元素5左右孩子为NULL,因此不用入队。直接执行出队列操作.

10.取队列首元素6,并将节点6的左右孩子入队。但是,元素6左右孩子为NULL,因此不用入队。直接执行出队列操作。
11.到此,队列元素已全部出队,层序遍历完成!
结果为:
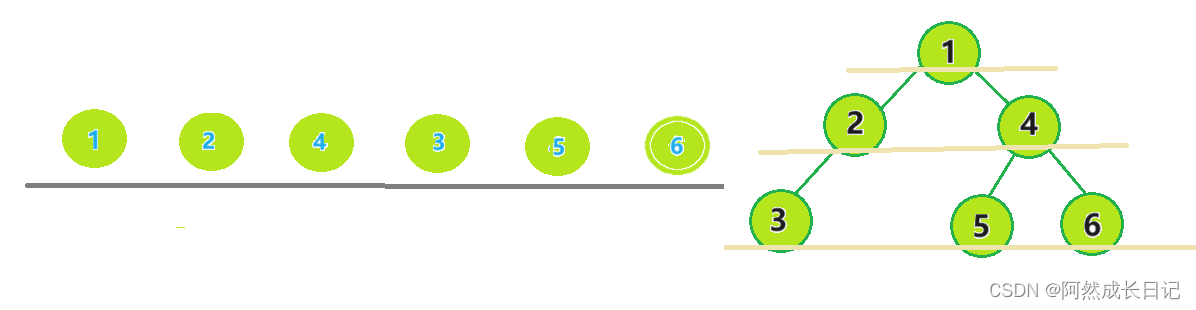
2.代码
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);printf("%d ", tmp->_data);if (tmp->_left){QueuePush(&q,tmp->_left);}if (tmp->_right){QueuePush(&q, tmp->_right);}QueuePop(&q);}printf("\n");QueueDestroy(&q);
}
3.测试结果

相关文章:

【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
优彩云采集器下载-免费优彩云采集器下载地址
免费优彩云采集器。您是否曾为了数据采集而感到头疼不已?是否一直在寻找一种能够轻松、高效地获取所需数据的方法?别着急,让我们一起来了解如何通过优彩云采集器解决这些问题,从而让您产生购买的欲望。 免费全自动采集发布批量管理…...

【Python】OJ 常用函数
这里写目录标题 一. math1. 求阶乘 - factorial()2. 绝对值 - fabs() 二. 容器的方法1. reverse() 三. Python 内置函数1. sort() 一. math 需要引入 math 包:import math 1. 求阶乘 - factorial() import math print(math.factorial(5))--------运行结果-------…...

【Vue】上万个字把事件处理讲解的淋漓尽致
hello,我是小索奇,精心制作的Vue系列教程持续更新哈,想要学习&巩固&避坑就一起学习吧~ 事件处理 事件的基本用法 重点内容 使用v-on:xxx缩写xxx绑定事件,其中 xxx 是事件名(回顾:v-bind缩写为冒号…...

Remmina中VNC、SSH和RDP的区别
Remmina 可以在 Linux 系统上对远程进行连接。它支持多种远程连接协议,包括 VNC(Virtual Network Computing)、SSH(Secure Shell)和 RDP(Remote Desktop Protocol)。这些协议用于实现不同类型的…...
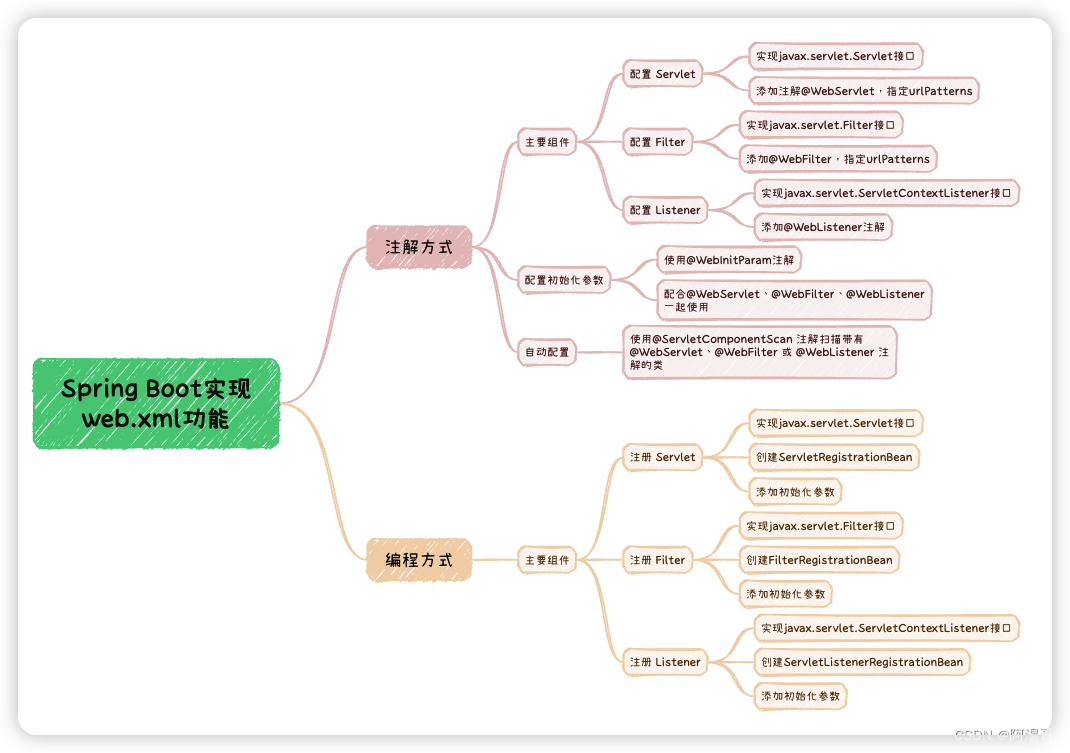
Spring Boot实现web.xml功能
Spring Boot实现web.xml功能 1. 基于注解实现1.1 组件注册1.2 WebInitParam注解 2. 基于编码实现2.1 Servlet & Filter2.2 Listener 3. 总结 在Spring Boot中,不再需要使用传统的 web.xml 文件来配置web应用的功能,Spring Boot支持通过注解和基于代码…...
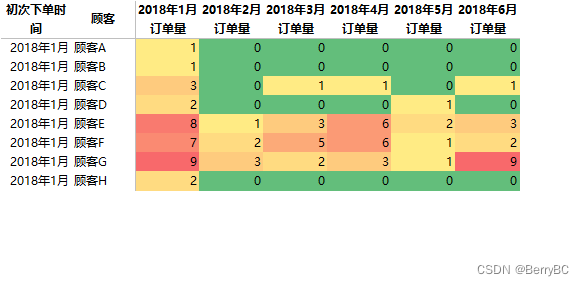
陆拾捌- 如何通过数据影响决策(三)
一、如何正确的引导别人? 引导与误导的区别是什么? 看下面这广告图 单看上面大字的结果,感觉好像真的使用过的人均觉得有好处 可如果我们看下面的细字 对111位连续14天食用(本产品)的燕麦片非重度使用者所做调研… 从…...

VMware 三种网络连接模式
VMware虚拟机的三种网络连接模式:桥接,NAT,仅主机。 网卡vmnet0,vmnet1,vmnet8区别。 在VMware中,虚拟机的网络连接主要是由VMware创建的虚拟交换机负责实现的,VMware可以根据需要创建多个虚拟网络。 VMware的虚拟网…...

Scikit-Learn快速生成分类数据集
假如你学习了新的分类算法并想进一步探索研究、尝试不同的超参数评估模型性能,但问题是你找不到好的数据集用于实验。幸运的是Scikit-Learn 提供的 make_classification() 方法可以创建不同类型的数据集,它可以生成不同类型的数据集:二分类、…...

西门子 S7 协议解析
目录 1 建立连接 2 读数据 3 写数据 1 建立连接 03 00 00 16 11 E0 00 00 00 01 00 C1 02 10 00 C2 02 03 01 C0 01 0A (第一次握手报文) 03 00 报文头 00 16 数据总长度:22 11 E0 00 00 00 01 00 C1 02 10 00 C2 02 03 01 C0 01 0A 报文结束…...

一、python解题——求序列最长递增
解题代码: import os import sys# 请在此输入您的代码 n int(input()) a list(map(int, input().split())) # 创建一个初始元素全为1的列表,用来存放每个递增序列的长度 b [1 for x in range(0, n)] # 设置num,用来控制b列表的下标 num …...

【Java 基础篇】Java线程:volatile关键字与原子操作详解
在多线程编程中,确保线程之间的可见性和数据一致性是非常重要的。Java中提供了volatile关键字和原子操作机制,用于解决这些问题。本文将深入讨论volatile关键字和原子操作的用法,以及它们在多线程编程中的重要性和注意事项。 volatile关键字…...

992. K 个不同整数的子数组
992. K 个不同整数的子数组 给定一个正整数数组 nums和一个整数 k,返回 nums 中 「好子数组」 的数目。 如果 nums 的某个子数组中不同整数的个数恰好为 k,则称 nums 的这个连续、不一定不同的子数组为 「好子数组 」。 例如,[1,2,3,1,2] 中…...

Vue 使用vue-cli构建SPA项目(超详细)
目录 一、什么是vue-cli 二,构建SPA项目 三、 运行SPA项目 前言: 在我们搭建SPA项目时候,我们必须去检查我们是否搭建好NodeJS环境 cmd窗口输入以下指令:去检查 node -v npm -v 一、什么是vue-cli Vue CLI(Vu…...

SpringBoot工程模板
spring脚手架:https://start.spring.io/ <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocati…...
学习SLAM:SLAM进阶(十)暴力更改ROS中的PCL库
话不多说,上活 1.1 为什么要这么做 项目中有依赖。。。。 1.2 安装VTK7.1.1 PCL1.8.0 略 1.3 移植到ROS 删除ROS依赖的vtk6.2和PCL1.8.0的动态链接库: liugongweiubuntu:~$ sudo mv /usr/lib/x86_64-linux-gnu/libvtk* Desktop/lib/ [sudo] password fo…...
js 事件流、事件冒泡、事件捕获、阻止事件的传播
事件流 js 事件的执行过程分为捕获阶段(由外层节点传播到内层节点)和冒泡阶段(由内层节点传播到外层节点),即先执行捕获阶段的代码,后执行冒泡阶段的代码 事件冒泡 js 事件中的代码默认在冒泡阶段执行&…...

一家美国公司被黑,一个拉美国家政务服务瘫痪
政务系统承包商遭勒索攻击,导致哥伦比亚国家政务服务陷入瘫痪。 据报道,9月19日哥伦比亚的多个重要政府部门正在应对一次勒索软件攻击,官员们被迫大幅变更部门运作方式。 哥伦比亚卫生和社会保护部、司法部门、工商监管部门上周宣布&#x…...

c++ QT 十八位时间戳转换
先说一下UTC: 它是协调世界时间,又称世界统一时间、世界标准时间、国际协调时间,简称UTC UTC时间与本地时间关系:UTC 时间差本地时间 如果UTC时间是 2015-05-01 00:00:00 那么北京时间就是 2015-05-01 08:00:00 解释:…...
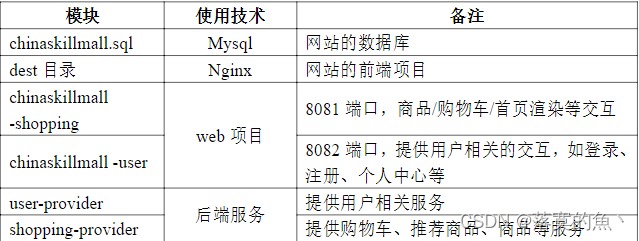
全国职业技能大赛云计算--高职组赛题卷④(容器云)
全国职业技能大赛云计算--高职组赛题卷④(容器云) 第二场次题目:容器云平台部署与运维任务1 Docker CE及私有仓库安装任务(5分)任务2 基于容器的web应用系统部署任务(15分)任务3 基于容器的持续…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
