多传感器融合定位十一-基于滤波的融合方法Ⅱ
多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 1. 编码器运动模型及标定
- 1.1 编码器基础知识
- 1.2 编码器运动模型
- 1.2.1 旋转半径求解
- 1.2.2 角速度求解
- 1.2.3 线速度求解
- 1.2.4 位姿求解
- 1.3 编码器的标定
- 1.3.1 轮子半径标定
- 1.3.2 轮子与底盘中心距离标定
- 2. 融合编码器的滤波方法
- 2.1 核心思路
- 2.2 观测量定义
- 2.3 观测方程推导
- 3. 融合运动约束的滤波方法
- 4. 融合点云特征的滤波方法
- 4.1 整体思路
- 4.2 滤波模型
- 4.3 位姿更新
- 4.4 相似工作
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转:
- 多传感器融合定位一-3D激光里程计其一:ICP
- 多传感器融合定位二-3D激光里程计其二:NDT
- 多传感器融合定位三-3D激光里程计其三:点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四:点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
1. 编码器运动模型及标定
1.1 编码器基础知识

编码器感应轮子的旋转,并在旋转时输出脉冲,脉冲数与转过的角度呈线性比例关系。
脉冲对应的是角度增量,有时也用增量除以时间,转成轮子转动的角速度输出。
需要注意的是,编码器只是各种转角测量方式中的一种,其他还有轮速计、霍尔传感器等,本课程以编码器为例子讲解模型,但同样适用于其他形式的传感器。
编码器安装方式有单轮、双轮、三轮,本课程推导仅围绕双轮差分模型进行展开。
该模型中,需要用到以下变量:
- rL\boldsymbol{r}_LrL:左轮半径
- rR\boldsymbol{r}_RrR:右轮半径
- d\boldsymbol{d}d:轮子离底盘中心的距离
- ωL\boldsymbol{\omega}_LωL:左轮自转角速度
- ωR\boldsymbol{\omega_R}ωR:右轮自转角速度
- vL\boldsymbol{v}_LvL:左轮线速度
- vR\boldsymbol{v}_RvR:右轮线速度
实际使用时,标定完成后, rL\boldsymbol{r}_LrL、rR\boldsymbol{r}_RrR、d\boldsymbol{d}d 为固定参数, ωL\boldsymbol{\omega}_LωL 和 ωR\boldsymbol{\omega}_RωR 为测量值,而 vL\boldsymbol{v}_LvL 和 vR\boldsymbol{v}_RvR 可以通过下式计算得到:
vL=ωLrLvR=ωRrR\begin{aligned} \boldsymbol{v}_L & =\boldsymbol{\omega}_L \boldsymbol{r}_L \\ \boldsymbol{v}_R & =\boldsymbol{\omega}_R \boldsymbol{r}_R \end{aligned} vLvR=ωLrL=ωRrR
1.2 编码器运动模型

运动模型的作用是,使用前述已知量,求解以下变量:
ω\boldsymbol{\omega}ω : 底盘中心的角速度
v\boldsymbol{v}v : 底盘中心的线速度
r\boldsymbol{r}r : 底盘中心圆弧运动旋转半径
1.2.1 旋转半径求解
双轮差分模型下,左右轮圆弧运动的角速度相等,且等于底盘中心圆弧运动的角速度(两个轮子的自转角速度是相同的),因此有:
ω=vLr−d=vRr+d\boldsymbol{\omega}=\frac{\boldsymbol{v}_L}{\boldsymbol{r}-\boldsymbol{d}}=\frac{\boldsymbol{v}_R}{\boldsymbol{r}+\boldsymbol{d}} ω=r−dvL=r+dvR由此可以得出:
vL(r+d)=vR(r−d)\boldsymbol{v}_L(\boldsymbol{r}+\boldsymbol{d})=\boldsymbol{v}_R(\boldsymbol{r}-\boldsymbol{d}) vL(r+d)=vR(r−d)移项可得:
(vR−vL)r=(vR+vL)d\left(\boldsymbol{v}_R-\boldsymbol{v}_L\right) \boldsymbol{r}=\left(\boldsymbol{v}_R+\boldsymbol{v}_L\right) \boldsymbol{d} (vR−vL)r=(vR+vL)d从而可以得到:
r=vR+vLvR−vLd\boldsymbol{r}=\frac{\boldsymbol{v}_R+\boldsymbol{v}_L}{\boldsymbol{v}_R-\boldsymbol{v}_L} \boldsymbol{d} r=vR−vLvR+vLd
1.2.2 角速度求解
把旋转半径的求解结果,代入角速度公式,即可得到:
ω=vLvR+vLvR−vLd−d=vR−vL2d\boldsymbol{\omega}=\frac{\boldsymbol{v}_L}{\frac{\boldsymbol{v}_R+\boldsymbol{v}_L}{\boldsymbol{v}_R-\boldsymbol{v}_L} \boldsymbol{d}-\boldsymbol{d}}=\frac{\boldsymbol{v}_R-\boldsymbol{v}_L}{2 \boldsymbol{d}} ω=vR−vLvR+vLd−dvL=2dvR−vL
1.2.3 线速度求解
利用旋转角速度和旋转半径的结果,可以直接得到线速度:
v=ωr=vR−vL2dvR+vLvR−vLd=vR+vL2\boldsymbol{v}=\boldsymbol{\omega} \boldsymbol{r}=\frac{\boldsymbol{v}_R-\boldsymbol{v}_L}{2 \boldsymbol{d}} \frac{\boldsymbol{v}_R+\boldsymbol{v}_L}{\boldsymbol{v}_R-\boldsymbol{v}_L} \boldsymbol{d}=\frac{\boldsymbol{v}_R+\boldsymbol{v}_L}{2} v=ωr=2dvR−vLvR−vLvR+vLd=2vR+vL
1.2.4 位姿求解

假设 xk,yk,θk\boldsymbol{x}_k, \boldsymbol{y}_k, \boldsymbol{\theta}_kxk,yk,θk 为当前时刻位姿,xk−1,yk−1,θk−1\boldsymbol{x}_{k-1}, \boldsymbol{y}_{k-1}, \boldsymbol{\theta}_{k-1}xk−1,yk−1,θk−1 为上一时刻的位姿,则有:
θk=θk−1+ωΔtxk=xk−1+vΔtcos(θk−1)yk=yk−1+vΔtsin(θk−1)\begin{aligned} & \boldsymbol{\theta}_k=\boldsymbol{\theta}_{k-1}+\boldsymbol{\omega} \Delta t \\ & \boldsymbol{x}_k=\boldsymbol{x}_{k-1}+\boldsymbol{v} \Delta t \cos \left(\boldsymbol{\theta}_{\boldsymbol{k - 1}}\right) \\ & \boldsymbol{y}_k=\boldsymbol{y}_{k-1}+\boldsymbol{v} \Delta t \sin \left(\boldsymbol{\theta}_{\boldsymbol{k}-1}\right) \end{aligned} θk=θk−1+ωΔtxk=xk−1+vΔtcos(θk−1)yk=yk−1+vΔtsin(θk−1)其中:
Δt=tk−tk−1\Delta t=t_k-t_{k-1} Δt=tk−tk−1
1.3 编码器的标定
标定可以理解为运动模型求解过程的反向过程,具体是指在已知底盘中心线速度、角速度的情况下,求解轮子半径、轮子离底盘中心距离等。
已知量:
vvv:底盘中心的线速度
ω\omegaω:底盘中心的角速度
待求解量:
rL\boldsymbol{r}_LrL:左轮半径
rR\boldsymbol{r}_RrR:右轮半径
d\boldsymbol{d}d:轮子离底盘中心的距离
实际标定时,线速度、角速度由其他传感器提供(比如雷达点云和地图匹配),且为了简化模型,认为雷达装在底盘中心正上方。(这里雷达最好的方法是先建好一个点云地图,然后在点云地图里面匹配,然后拿它做观测,去提供线速度和角速度的结果,而不要用激光里程计-----里程计本身就是有累计误差的)
1.3.1 轮子半径标定
由于速度的求解公式为:
v=vR+vL2=ωRrR+ωLrL2\boldsymbol{v}=\frac{\boldsymbol{v}_R+\boldsymbol{v}_L}{2}=\frac{\boldsymbol{\omega}_R \boldsymbol{r}_R+\boldsymbol{\omega}_L \boldsymbol{r}_L}{2} v=2vR+vL=2ωRrR+ωLrL它可以重新写为:
[ωRωL][rRrL]=2v\left[\begin{array}{ll} \boldsymbol{\omega}_R & \boldsymbol{\omega}_L \end{array}\right]\left[\begin{array}{l} \boldsymbol{r}_R \\ \boldsymbol{r}_L \end{array}\right]=2 \boldsymbol{v} [ωRωL][rRrL]=2v当有多组测量值时,可以构成如下方程组:
[ωR0ωL0ωR1ωL1⋮⋮ωRNωLN][rRrL]=[2v02v1⋮2vN]\left[\begin{array}{cc} \boldsymbol{\omega}_{R 0} & \boldsymbol{\omega}_{L 0} \\ \boldsymbol{\omega}_{R 1} & \boldsymbol{\omega}_{L 1} \\ \vdots & \vdots \\ \boldsymbol{\omega}_{R N} & \boldsymbol{\omega}_{L N} \end{array}\right]\left[\begin{array}{l} \boldsymbol{r}_R \\ \boldsymbol{r}_L \end{array}\right]=\left[\begin{array}{c} 2 \boldsymbol{v}_0 \\ 2 \boldsymbol{v}_1 \\ \vdots \\ 2 \boldsymbol{v}_N \end{array}\right] ωR0ωR1⋮ωRNωL0ωL1⋮ωLN[rRrL]=2v02v1⋮2vN这是典型的最小二乘问题,可用最小二乘标准形式计算。
1.3.2 轮子与底盘中心距离标定
由于角速度的求解公式为:
ω=vR−vL2d\boldsymbol{\omega}=\frac{\boldsymbol{v}_R-\boldsymbol{v_L}}{2 \boldsymbol{d}} ω=2dvR−vL在经过轮子半径标定之后,分子上的两项可认为是已知量,因此可以得到:
d=vR−vL2ω\boldsymbol{d}=\frac{\boldsymbol{v}_R-\boldsymbol{v}_L}{2 \boldsymbol{\omega}} d=2ωvR−vL虽然可直接求解,但是为了抑制噪声带来的影响,因多次采样计算取平均。
2. 融合编码器的滤波方法
2.1 核心思路
在上一节课滤波模型的基础上增加编码器进行融合,有一种非常简单的方法,即使用编码器解算的速度作为观测量,加入原来模型的观测方程中,而其他环节保持不变。
2.2 观测量定义
编码器提供的是载体系下的速度观测,在前 (x)(\mathrm{x})(x)-左 (y)(\mathrm{y})(y)-上(z)坐标系的定义下,x\mathrm{x}x 方向的速度分量是已知的 vxb=vm\boldsymbol{v}_x^b=\boldsymbol{v}_mvxb=vm。 另外,在以车作为载体的情况下,由于车的侧向和天向没有运动,因此又有 vyb=0\boldsymbol{v}_y^b=0vyb=0,vzb=0\boldsymbol{v}_z^b=0vzb=0。
基于此,我们可以认为 bbb 系 3 个维度的速度分量都是可观测的。
2.3 观测方程推导
由于导航解算得到的是 www 系下得速度,而速度观测是 bbb 系下得,因此需要推导二者之间的误差关系,才能得到相应的观测方程。
推导方法仍按照第6讲的固定套路进行。
- 写出不考虑误差时的方程:
vb=Rbwvw\boldsymbol{v}^b=\boldsymbol{R}_{b w} \boldsymbol{v}^w vb=Rbwvw - 写出考虑误差时的方程:
v~b=R~bwv~w\tilde{\boldsymbol{v}}^b=\tilde{\boldsymbol{R}}_{b w} \tilde{\boldsymbol{v}}^w v~b=R~bwv~w - 写出真实值与理想值之间的关系:
v~b=vb+δvbv~w=vw+δvwR~bw=R~wbT=(Rwb(I+[δθ]×))T=(I−[δθ]×)Rbw\begin{aligned} & \tilde{\boldsymbol{v}}^b=\boldsymbol{v}^b+\delta \boldsymbol{v}^b \\ & \tilde{\boldsymbol{v}}^w=\boldsymbol{v}^w+\delta \boldsymbol{v}^w \\ & \tilde{\boldsymbol{R}}_{b w}=\tilde{\boldsymbol{R}}_{w b}^T=\left(\boldsymbol{R}_{w b}\left(\boldsymbol{I}+[\delta \boldsymbol{\theta}]_{\times}\right)\right)^T \\ & =\left(\boldsymbol{I}-[\delta \boldsymbol{\theta}]_{\times}\right) \boldsymbol{R}_{b w} \end{aligned} v~b=vb+δvbv~w=vw+δvwR~bw=R~wbT=(Rwb(I+[δθ]×))T=(I−[δθ]×)Rbw - 把3)中的关系带入2)式:
vb+δvb=(I−[δθ]×)Rbw(vw+δvw)\boldsymbol{v}^b+\delta \boldsymbol{v}^b=\left(\boldsymbol{I}-[\delta \boldsymbol{\theta}]_{\times}\right) \boldsymbol{R}_{b w}\left(\boldsymbol{v}^w+\delta \boldsymbol{v}^w\right) vb+δvb=(I−[δθ]×)Rbw(vw+δvw) - 把1)中的关系带入4)式:
Rbwvw+δvb=(I−[δθ]×)Rbw(vw+δvw)\boldsymbol{R}_{b w} \boldsymbol{v}^w+\delta \boldsymbol{v}^b=\left(\boldsymbol{I}-[\delta \boldsymbol{\theta}]_{\times}\right) \boldsymbol{R}_{b w}\left(\boldsymbol{v}^w+\delta \boldsymbol{v}^w\right) Rbwvw+δvb=(I−[δθ]×)Rbw(vw+δvw) - 化简方程:
δvb=Rbwδvw−[δθ]×Rbwvw=Rbwδvw−[δθ]×vb=Rbwδvw+[vb]×δθ\begin{aligned} \delta \boldsymbol{v}^b & =\boldsymbol{R}_{b w} \delta \boldsymbol{v}^w-[\delta \boldsymbol{\theta}]_{\times} \boldsymbol{R}_{b w} \boldsymbol{v}^w \\ & =\boldsymbol{R}_{b w} \delta \boldsymbol{v}^w-[\delta \boldsymbol{\theta}]_{\times} \boldsymbol{v}^b \\ & =\boldsymbol{R}_{b w} \delta \boldsymbol{v}^w+\left[\boldsymbol{v}^b\right]_{\times} \delta \boldsymbol{\theta} \end{aligned} δvb=Rbwδvw−[δθ]×Rbwvw=Rbwδvw−[δθ]×vb=Rbwδvw+[vb]×δθ
根据前一章内容,状态量为
δx=[δpδvδθδbaδbω]\delta \boldsymbol{x}=\left[\begin{array}{c} \delta \boldsymbol{p} \\ \delta \boldsymbol{v} \\ \delta \boldsymbol{\theta} \\ \delta \boldsymbol{b}_a \\ \delta \boldsymbol{b}_\omega \end{array}\right] δx=δpδvδθδbaδbω而融合编码器以后,观测量变为
y=[δp‾δv‾bδθ‾]\boldsymbol{y}=\left[\begin{array}{c} \delta \overline{\boldsymbol{p}} \\ \delta \overline{\boldsymbol{v}}^b \\ \delta \overline{\boldsymbol{\theta}} \end{array}\right] y=δpδvbδθ其中 δv‾b\delta \overline{\boldsymbol{v}}^bδvb 的观测值可以通过下式获得
δv‾b=v~b−vb=R~bwv~w−[vm00]\delta \overline{\boldsymbol{v}}_b=\tilde{\boldsymbol{v}}^b-\boldsymbol{v}^b=\tilde{\boldsymbol{R}}_{b w} \tilde{\boldsymbol{v}}^w-\left[\begin{array}{c} \boldsymbol{v}_m \\ 0 \\ 0 \end{array}\right] δvb=v~b−vb=R~bwv~w−vm00此时的观测方程 y=Gtδx+Ctn\boldsymbol{y}=\boldsymbol{G}_t \delta \boldsymbol{x}+\boldsymbol{C}_t \boldsymbol{n}y=Gtδx+Ctn 中的各变量应重新写为
Gt=[I300000Rbw[vb]×0000I300]Ct=[I3000I3000I3]n=[nδpˉxnδpˉynδpˉznδvˉxbnδvˉybnδvˉzbnδθˉxnδθˉynδθˉz]T\begin{aligned} & \boldsymbol{G}_t=\left[\begin{array}{ccccc} \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{R}_{b w} & {\left[\boldsymbol{v}^b\right]_{\times}} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \end{array}\right] \\ & \boldsymbol{C}_t=\left[\begin{array}{ccc} \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 \end{array}\right] \\ & \boldsymbol{n}=\left[\begin{array}{lllllllll} n_{\delta \bar{p}_x} & n_{\delta \bar{p}_y} & n_{\delta \bar{p}_z} & n_{\delta \bar{v}_x^b} & n_{\delta \bar{v}_y^b} & n_{\delta \bar{v}_z^b} & n_{\delta \bar{\theta}_x} & n_{\delta \bar{\theta}_y} & n_{\delta \bar{\theta}_z} \end{array}\right]^T \end{aligned} Gt=I3000Rbw00[vb]×I3000000Ct=I3000I3000I3n=[nδpˉxnδpˉynδpˉznδvˉxbnδvˉybnδvˉzbnδθˉxnδθˉynδθˉz]T随后,便可以使用新的观测方程,不改变其他方程,直接按照原有流程进行Kalman滤波融合。
3. 融合运动约束的滤波方法
很多时候,硬件平台并没有编码器,不能直接使用上一小节的模型,但是车本身的运动特性(即侧向速度和天向速度为0)仍然可以使用。
它对观测量带来的改变仅仅是少了一个维度(xxx 方向),而推导方法并没有改变,因此此处直接给出该融合模式下的推导结果。
新的观测量为
y=[δp‾[δv‾b]yzδθ‾]\boldsymbol{y}=\left[\begin{array}{c} \delta \overline{\boldsymbol{p}} \\ {\left[\delta \overline{\boldsymbol{v}}^b\right]_{y z}} \\ \delta \overline{\boldsymbol{\theta}} \end{array}\right] y=δp[δvb]yzδθ[∙]yz[\bullet]_{y z}[∙]yz 表示只取三维向量或矩阵的后2行
此时的观测方程 y=Gtδx+Ctn\boldsymbol{y}=\boldsymbol{G}_t \delta \boldsymbol{x}+\boldsymbol{C}_t \boldsymbol{n}y=Gtδx+Ctn 中的各变量应重新写为
Gt=[I300000[Rbw]yz[[vb]×]yz0000I300]Ct=[I3000I2000I3]n=[nδpˉxnδpˉynδpˉznδvˉybnδvˉzbnδθˉxnδθˉynδθˉz]T\begin{aligned} & \boldsymbol{G}_t=\left[\begin{array}{ccccc} \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & {\left[\boldsymbol{R}_{b w}\right]_{y z}} & {\left[\left[\boldsymbol{v}^b\right]_{\times}\right]_{y z}} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \end{array}\right] \\ & \boldsymbol{C}_t=\left[\begin{array}{ccc} \boldsymbol{I}_3 & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_2 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \boldsymbol{I}_3 \end{array}\right] \\ & \boldsymbol{n}=\left[\begin{array}{llllllll} n_{\delta \bar{p}_x} & n_{\delta \bar{p}_y} & n_{\delta \bar{p}_z} & n_{\delta \bar{v}_y^b} & n_{\delta \bar{v}_z^b} & n_{\delta \bar{\theta}_x} & n_{\delta \bar{\theta}_y} & n_{\delta \bar{\theta}_z} \end{array}\right]^T \end{aligned} Gt=I3000[Rbw]yz00[[vb]×]yzI3000000Ct=I3000I2000I3n=[nδpˉxnδpˉynδpˉznδvˉybnδvˉzbnδθˉxnδθˉynδθˉz]T随后的Kalman流程仍然与之前保持一致。
4. 融合点云特征的滤波方法
4.1 整体思路
以IMU做状态预测,以特征中的点-面距离、点-线距离为约束(观测),修正误差。
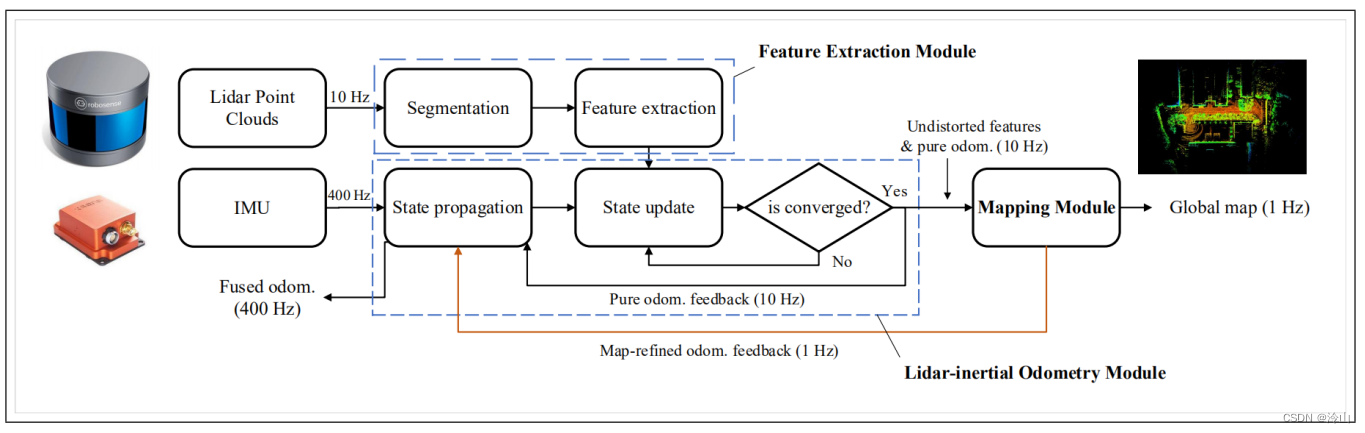
论文题目:LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation
4.2 滤波模型
-
状态定义
位姿定义:
xwbk:=[pwbk,qwbk]\mathbf{x}_w^{b_k}:=\left[\mathbf{p}_w^{b_k}, \mathbf{q}_w^{b_k}\right] xwbk:=[pwbk,qwbk]相对位姿相关:
xbk+1bk:=[pbk+1bk,vbk+1bk,qbk+1bk,ba,bg,gbk]\mathbf{x}_{b_{k+1}}^{b_k}:=\left[\mathbf{p}_{b_{k+1}}^{b_k}, \mathbf{v}_{b_{k+1}}^{b_k}, \mathbf{q}_{b_{k+1}}^{b_k}, \mathbf{b}_a, \mathbf{b}_g, \mathbf{g}^{b_k}\right] xbk+1bk:=[pbk+1bk,vbk+1bk,qbk+1bk,ba,bg,gbk]状态量:
δx:=[δp,δv,δθ,δba,δbg,δg]\delta \mathbf{x}:=\left[\delta \mathbf{p}, \delta \mathbf{v}, \delta \boldsymbol{\theta}, \delta \mathbf{b}_a, \delta \mathbf{b}_g, \delta \mathbf{g}\right] δx:=[δp,δv,δθ,δba,δbg,δg]状态量修正:
xbk+1bk=−xbk+1bk⊞δx=[−pbk+1bk+δp−vkbk+δv−qbk+1bk⊗exp(δθ)−ba+δba−bg+δbg−gbk+δg]\mathbf{x}_{b_{k+1}}^{b_k}={ }^{-} \mathbf{x}_{b_{k+1}}^{b_k} \boxplus \boldsymbol{\delta} \mathbf{x}=\left[\begin{array}{c} -\mathbf{p}_{b_{k+1}}^{b_k}+\boldsymbol{\delta} \mathbf{p} \\ -\mathbf{v}_k^{b_k}+\boldsymbol{\delta} \mathbf{v} \\ -\mathbf{q}_{b_{k+1}}^{b_k} \otimes \exp (\boldsymbol{\delta} \boldsymbol{\theta}) \\ -\mathbf{b}_a+\boldsymbol{\delta} \mathbf{b}_a \\ -\mathbf{b}_g+\delta \mathbf{b}_g \\ -\mathbf{g}^{b_k}+\boldsymbol{\delta} \mathbf{g} \end{array}\right] xbk+1bk=−xbk+1bk⊞δx=−pbk+1bk+δp−vkbk+δv−qbk+1bk⊗exp(δθ)−ba+δba−bg+δbg−gbk+δg其中 −xbk+1bk{ }^{-} \mathbf{x}_{b_{k+1}}^{b_k}−xbk+1bk 表示预测值。 -
状态方程
δx˙(t)=Ftδx(t)+Gtw\delta \dot{\mathbf{x}}(t)=\mathbf{F}_t \delta \mathbf{x}(t)+\mathbf{G}_t \mathbf{w} δx˙(t)=Ftδx(t)+Gtw其中
Ft=[0I000000−Rtbk[a^t]×−Rtbk0−I300−[ω^t]×0−I30000000000000000000]Gt=[0000−Rtbk0000−I30000I30000I30000]w=[naT,ngT,nbaT,nbgT]T\begin{aligned} \mathbf{F}_t & =\left[\begin{array}{cccccc} 0 & \mathbf{I} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & -\mathbf{R}_t^{b_k}\left[\hat{\mathbf{a}}_t\right]_{\times} & -\mathbf{R}_t^{b_k} & \mathbf{0} & -\mathbf{I}_3 \\ 0 & 0 & -\left[\hat{\omega}_t\right]_{\times} & \mathbf{0} & -\mathbf{I}_3 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \end{array}\right] \quad \mathbf{G}_t=\left[\begin{array}{cccc} \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ -\mathbf{R}_t^{b_k} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & -\mathbf{I}_3 & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{I}_3 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_3 \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \end{array}\right] \\ \mathbf{w} & =\left[\mathbf{n}_a^T, \mathbf{n}_g^T, \mathbf{n}_{b_a}^T, \mathbf{n}_{b_g}^T\right]^T \end{aligned} Ftw=000000I000000−Rtbk[a^t]×−[ω^t]×0000−Rtbk000000−I30000−I30000Gt=0−Rtbk000000−I3000000I3000000I30=[naT,ngT,nbaT,nbgT]T -
观测方程
观测的计算与loam中前后帧匹配的思想一致,都是计算 点-面、点-线的残差
其中
p^ilk=(Rlb)T(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)\hat{\mathbf{p}}_i^{l_k}=\left(\mathbf{R}_l^b\right)^T\left(\mathbf{R}_{b_{k+1}}^{b_k}\left(\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right)+\mathbf{p}_{b_{k+1}}^{b_k}-\mathbf{p}_l^b\right) p^ilk=(Rlb)T(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)为了计算观测方程,需要计算残差对状态量的雅可比
Hk=∂f∂p^ilk⋅∂p^ilk∂δx\mathbf{H}_k=\frac{\partial \mathbf{f}}{\partial \hat{\mathbf{p}}_i^{l_k}} \cdot \frac{\partial \hat{\mathbf{p}}_i^{l_k}}{\partial \delta \mathbf{x}} Hk=∂p^ilk∂f⋅∂δx∂p^ilk上式中包含两部分,第一部分已经讲过,此处只推导第 二部分。
除了旋转和平移外,残差项对其它量的导数均为 0 。
a.对平移求导
∂p^ilk∂δp=∂[(Rlb)⊤(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)]∂δp=∂[(Rlb)⊤pbk+1bk]∂δp=(Rlb)⊤\begin{aligned} & \frac{\partial \hat{\mathbf{p}}_i^{l_k}}{\partial \delta \mathbf{p}} \\ = & \frac{\partial\left[\left(\mathbf{R}_l^b\right)^{\top}\left(\mathbf{R}_{b_{k+1}}^{b_k}\left(\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right)+\mathbf{p}_{b_{k+1}}^{b_k}-\mathbf{p}_l^b\right)\right]}{\partial \delta \mathbf{p}} \\ = & \frac{\partial\left[\left(\mathbf{R}_l^b\right)^{\top} \mathbf{p}_{b_{k+1}}^{b_k}\right]}{\partial \delta \mathbf{p}} \\ = & \left(\mathbf{R}_l^b\right)^{\top} \end{aligned} ===∂δp∂p^ilk∂δp∂[(Rlb)⊤(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)]∂δp∂[(Rlb)⊤pbk+1bk](Rlb)⊤b.对旋转求导
∂p^ilk∂δx=∂[(Rlb)T(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)]∂δθ=(Rlb)T∂[Rbk+1bk(Rlbpilk+1+plb)]∂Rbk+1bk∂Rbk+1bk∂δθ=−(Rlb)T[Rbk+1bk(Rlbpilk+1+plb)]×Rbk+1bkJr−1(θ)=−(Rlb)TRbk+1bk[Rlbpilk+1+plb]×Rbkbk+1Rbk+1bkJr−1(θ)=−(Rlb)TRbk+1bk[Rlbpilk+1+plb]×Jr−1(θ)\begin{aligned} & \frac{\partial \hat{\mathbf{p}}_i^{l_k}}{\partial \delta \mathbf{x}} \\ = & \frac{\partial\left[\left(\mathbf{R}_l^b\right)^T\left(\mathbf{R}_{b_{k+1}}^{b_k}\left(\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right)+\mathbf{p}_{b_{k+1}}^{b_k}-\mathbf{p}_l^b\right)\right]}{\partial \delta \boldsymbol{\theta}} \\ = & \left(\mathbf{R}_l^b\right)^T \frac{\partial\left[\mathbf{R}_{b_{k+1}}^{b_k}\left(\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right)\right]}{\partial \mathbf{R}_{b_{k+1}}^{b_k}} \frac{\partial \mathbf{R}_{b_{k+1}}^{b_k}}{\partial \delta \boldsymbol{\theta}} \\ = & -\left(\mathbf{R}_l^b\right)^T\left[\mathbf{R}_{b_{k+1}}^{b_k}\left(\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right)\right]_{\times} \mathbf{R}_{b_{k+1}}^{b_k} \boldsymbol{J}_r^{-1}(\boldsymbol{\theta}) \\ = & -\left(\mathbf{R}_l^b\right)^T \mathbf{R}_{b_{k+1}}^{b_k}\left[\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right]_{\times} \mathbf{R}_{b_k}^{b_{k+1}} \mathbf{R}_{b_{k+1}}^{b_k} \boldsymbol{J}_r^{-1}(\boldsymbol{\theta}) \\ = & -\left(\mathbf{R}_l^b\right)^T \mathbf{R}_{b_{k+1}}^{b_k}\left[\mathbf{R}_l^b \mathbf{p}_i^{l_{k+1}}+\mathbf{p}_l^b\right]_{\times} \boldsymbol{J}_r^{-1}(\boldsymbol{\theta}) \end{aligned} =====∂δx∂p^ilk∂δθ∂[(Rlb)T(Rbk+1bk(Rlbpilk+1+plb)+pbk+1bk−plb)](Rlb)T∂Rbk+1bk∂[Rbk+1bk(Rlbpilk+1+plb)]∂δθ∂Rbk+1bk−(Rlb)T[Rbk+1bk(Rlbpilk+1+plb)]×Rbk+1bkJr−1(θ)−(Rlb)TRbk+1bk[Rlbpilk+1+plb]×Rbkbk+1Rbk+1bkJr−1(θ)−(Rlb)TRbk+1bk[Rlbpilk+1+plb]×Jr−1(θ)预测 :
δxtτ=(I+FtτΔt)δxtτ−1Ptτ=(I+FtτΔt)Ptτ−1(I+FtτΔt)T+(GiτΔt)Q(GttΔt)TKk,j=PkHk,jT(Hk,jPkHk,jT+Jk,jMkJk,jT)−1\begin{aligned} & \delta \mathbf{x}_{t_\tau}=\left(\mathbf{I}+\mathbf{F}_{t_\tau} \Delta t\right) \delta \mathbf{x}_{t_{\tau-1}} \\ & \mathbf{P}_{t_\tau}=\left(\mathbf{I}+\mathbf{F}_{t_\tau} \Delta t\right) \mathbf{P}_{t_{\tau-1}}\left(\mathbf{I}+\mathbf{F}_{t_\tau} \Delta t\right)^T+\left(\mathbf{G}_{i_\tau} \Delta t\right) \mathbf{Q}\left(\mathbf{G}_{t_t} \Delta t\right)^T \\ & \mathbf{K}_{k, j}=\mathbf{P}_k \mathbf{H}_{k, j}^T\left(\mathbf{H}_{k, j} \mathbf{P}_k \mathbf{H}_{k, j}^T+\mathbf{J}_{k, j} \mathbf{M}_k \mathbf{J}_{k, j}^T\right)^{-1} \end{aligned} δxtτ=(I+FtτΔt)δxtτ−1Ptτ=(I+FtτΔt)Ptτ−1(I+FtτΔt)T+(GiτΔt)Q(GttΔt)TKk,j=PkHk,jT(Hk,jPkHk,jT+Jk,jMkJk,jT)−1迭代观测: Δxj=Kk,j(Hk,jδxj−f(−xbk+1bk⊞δxj))\Delta \mathbf{x}_j=\mathbf{K}_{k, j}\left(\mathbf{H}_{k, j} \delta \mathbf{x}_j-f\left({ }^{-} \mathbf{x}_{b_{k+1}}^{b_k} \boxplus \boldsymbol{\delta} \mathbf{x}_j\right)\right)Δxj=Kk,j(Hk,jδxj−f(−xbk+1bk⊞δxj))
δxj+1=δxj+Δxj\delta \mathbf{x}_{j+1}=\delta \mathbf{x}_j+\Delta \mathbf{x}_j δxj+1=δxj+Δxj后验方差: Pk+1=(I−Kk,nHk,n)Pk(I−Kk,nHk,n)T+Kk,nMkKk,nT\mathbf{P}_{k+1}=\left(\mathbf{I}-\mathbf{K}_{k, n} \mathbf{H}_{k, n}\right) \mathbf{P}_k\left(\mathbf{I}-\mathbf{K}_{k, n} \mathbf{H}_{k, n}\right)^T+\mathbf{K}_{k, n} \mathbf{M}_k \mathbf{K}_{k, n}^TPk+1=(I−Kk,nHk,n)Pk(I−Kk,nHk,n)T+Kk,nMkKk,nT
4.3 位姿更新
xwbk+1=[pwbk+1qwbk+1]=[Rbkbk+1(pwbk−pbk+1bk)qbkbk+1⊗qwbk]\mathbf{x}_w^{b_{k+1}}=\left[\begin{array}{c} \mathbf{p}_w^{b_{k+1}} \\ \mathbf{q}_w^{b_{k+1}} \end{array}\right]=\left[\begin{array}{c} \mathbf{R}_{b_k}^{b_{k+1}}\left(\mathbf{p}_w^{b_k}-\mathbf{p}_{b_{k+1}}^{b_k}\right) \\ \mathbf{q}_{b_k}^{b_{k+1}} \otimes \mathbf{q}_w^{b_k} \end{array}\right] xwbk+1=[pwbk+1qwbk+1]=[Rbkbk+1(pwbk−pbk+1bk)qbkbk+1⊗qwbk]
4.4 相似工作
论文题目:FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter
相关文章:

多传感器融合定位十一-基于滤波的融合方法Ⅱ
多传感器融合定位十一-基于滤波的融合方法Ⅱ1. 编码器运动模型及标定1.1 编码器基础知识1.2 编码器运动模型1.2.1 旋转半径求解1.2.2 角速度求解1.2.3 线速度求解1.2.4 位姿求解1.3 编码器的标定1.3.1 轮子半径标定1.3.2 轮子与底盘中心距离标定2. 融合编码器的滤波方法2.1 核心…...
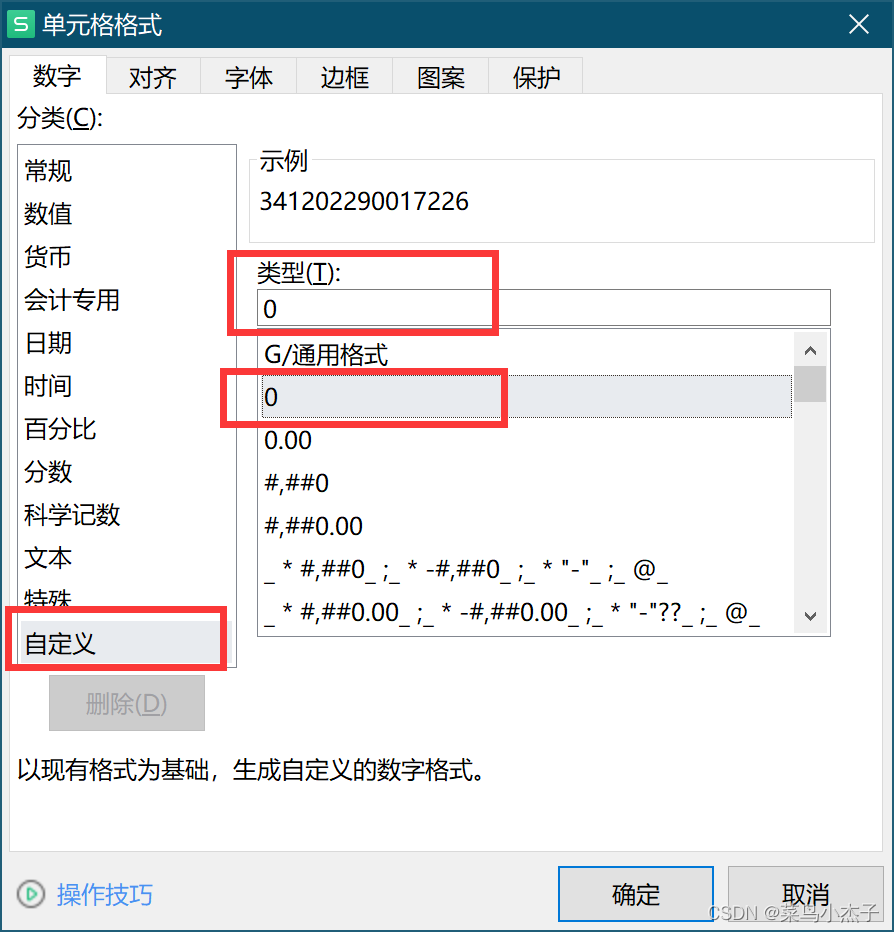
JAVA使用poi解析execl解决数值被转为科学计数法(如:手机号、身份证号、电话、等)解决方法
1、原由 大家都知道数字在EXCEL表格中存储时有两种表现形式。1.数字作为数值存储。当数字作为数值存储时,单元格中的数字可以参与数学运算。2.数字作为文本存储。当数字作为文本存储时,单元格中的数值不能够参与数学运算。 数字作为文本存储时,如果没有更…...
的使用)
hive中substring_index()的使用
substring_index(str,delim,count)str:要处理的字符串delim:分隔符count:计数例子:strwww.wikibt.comsubstring_index(str,.,1)结果是:wwwsubstring_index(str,.,2)结果是:www.wikibt如果count是正数,那么就是从左往右数ÿ…...

LocalDateTime设置时间的年、月、日、时、分、秒、纳秒
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 方法介绍 withYear(int year) 指定日期的…...
C语言rand和srand用法详解
在实际编程中,我们经常需要生成随机数,例如,贪吃蛇游戏中在随机的位置出现食物,扑克牌游戏中随机发牌。在C语言中,我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数,它的用法为ÿ…...

安装作业
1、安装方法 mysql安装常见的方法有四种 序号安装方式说明1yum\rpm简单、快速,不能定制参数2二进制解压,简单配置就可使用 免安装 mysql-a.b.c-linux2.x-x86_64.tar.gz3源码编译可以定制参数,安装时间长 mysql-a.b.c.tar.gz4源码制成rpm包把…...

电压放大器在非共线混频方法检测混凝土中的应用
实验名称:电压放大器在非共线混频方法检测混凝土中的应用研究方向:无损检测测试目的:无损检测是在不损伤或不干扰待测物体的结构材料的情况下,对其内部损伤进行探测的方法。传统无损检测法在仪器携带,操作程序…...
二十四、Gtk4-GtkExpression
GtkExpression是一种基本类型。它不是GObject的后代。GtkExpression提供了一种描述对值的引用的方法。GtkExpression需要求值才能获得值。 它类似于算术计算。 1 2 3 12是一个表达式。给出了计算的方法。3是来自表达式的值。求值是计算表达式并得到值。 GtkExpression是一种…...

Oracle Dataguard(主库为 Oracle rac 集群)配置教程(02)—— Oracle RAC 主库的相关操作
Oracle Dataguard(主库为 Oracle rac 集群)配置教程(02)—— Oracle RAC 主库的相关操作 / 本专栏详细讲解 Oracle Dataguard(Oracle 版本为11g,主库为双节点 Oracle rac 集群)的配置过程。主要…...

midjournery AI绘画使用指南
midjournery AI绘画使用指南 基于Discord的Midjournery配置: https://www.bilibili.com/video/BV16d4y1A7Zq/?spm_id_from333.337.search-card.all.click&vd_source9c3ca9555620bed64bdee27ae49d37cf 使用原则 使用midjournery绘画的原则是给出对脑海中某个…...

iptables防火墙SNAT和DNAT
iptables防火墙SNAT和DNAT一、SNAT原理和应用1、SNAT原理2、SNAT应用环境3、SNAT转换前提条件二、SNAT案列1、实验需求2、实验环境3、实验目的三、DNAT原理和应用1、DNAT原理2、DNAT 应用环境3、DNAT转换的前提条件四、DNAT案列总结一、SNAT原理和应用 1、SNAT原理 SNAT原理:…...
python | 第二章考试题和练习题
一、考试题 1、turtle八边形绘制 问题描述: 使用turtle库,绘制一个八边形。 参考代码: import turtle as t t.pensize(2) for i in range(8):t.fd(100)t.left(45) 2、turtle八角图形绘制 问题描述: 使用turtle库,…...

Mysql 存储引擎设计:xa协议相关接口功能及实现
需要对接的接口以及每个接口的实现 recovery 阶段 此阶段由 xa.cc 文件中的 xarecover_handlerton() 函数完成,它通过三个接口实现与存储引擎的沟通:recover(),commit_by_xid() ,rollback_by_xid()。其流程如下: 此…...
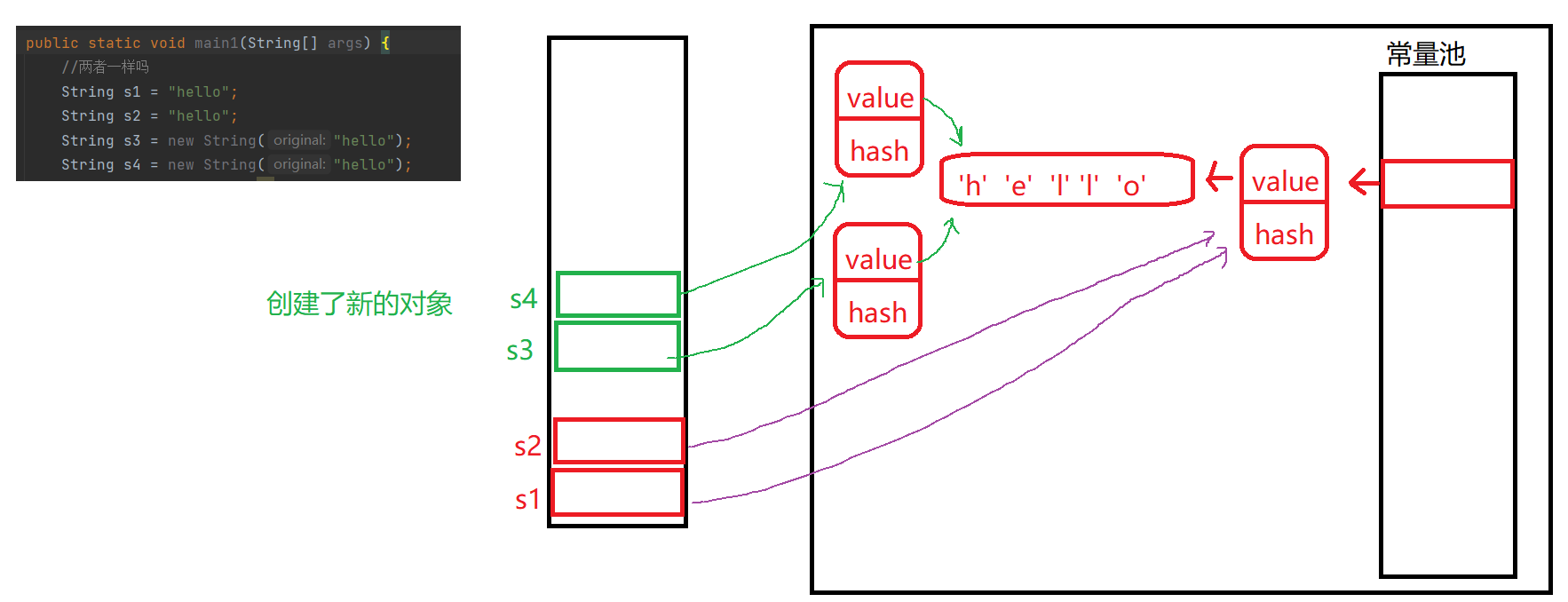
字符串常量池
1.创建对象的思考下面两种创建字符串的方式一样吗?public static void main(String[] args) {//两者一样吗String s1 "hello";String s2 "hello";String s3 new String("hello");String s4 new String("hello");System…...

让技术更有温度,腾讯Light 点亮公益之光
蓝天白云,远处是广东最长跨海大桥——南澳大桥,一艘小船在海面驶过,近处一头中华白海豚露出水面。在第三届腾讯Light技术公益创造营上,海南智渔可持续发展研究中心科学总监郑锐强为我们展现这样一幅人与自然和平相处的美好画面。随…...
电子采购一体化解决方案
企事业数字化转型专家,提供各类应用解决方案。您身边的赋能小助手! 文章目录前言一、当下采购的痛点二、解决方案-供应商管理1.供应商管理三、解决方案-企业询价、供应商报价管理四、解决方案-采购订单五、送货、到货、订单管理总结前言 随着各类产业链…...
SAP COPA 获利能力分析深度解析
一、获利分析配置及相关值概述 二、配置:组织结构 2.1 定义经营范围-KEP8 2.2 维护经营关注点-KEA0 2.3 获利能力分析类型解析 2.4 控制范围分配给经营范围-KEKK 三、配置:数据结构-KEA0 3.1 特征字段 3.1.1 特征字段类别 3.1.2 维护特征字段-K…...
Java学习记录day6
书接上回 类与对象 static关键字 static的作用: 修饰一个属性:声明为static的变量实质上就是一个全局变量,其生命周期为从类被加载开始一直到程序结束;修饰方法:无须本类的对象也可以调用该方法;修饰一个类&#x…...

ubuntu 使用 adb 工具卸载鸿蒙系统预装软件
准备工作 打开 USB 调试 进入 “设置->关于手机” 连续点击版本号, 直到有提示开启了"开发人员选项" 进入 “设置->系统和更新->开发人员选项”, 打开 USB 调式, 顺便可以把"自动系统更新"关了 下载 adb 工具 官方地址: https://developer.an…...
Jmeter in Linux - 在Linux系统使用Jmeter的坑
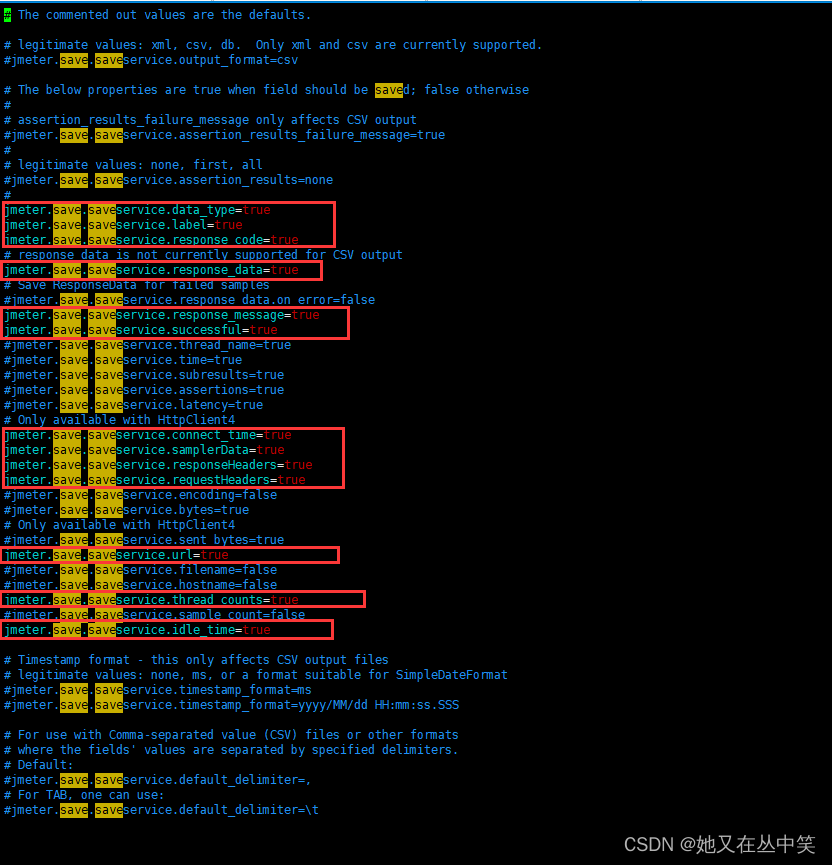
Jmeter in Linux - 在Linux系统使用Jmeter的坑Jmeter in Linux系列目录:o.a.j.JMeter: Error in NonGUIDriver起因错误分析:解决方案:解析日志没有展示请求和响应信息起因解决方案:注意Jmeter in Linux系列目录: 【如…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【JVM面试篇】高频八股汇总——类加载和类加载器
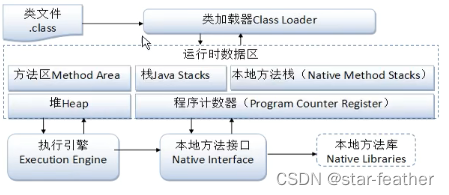
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
