轮换对称性
二重积分
- 普通对称性–D关于 y = x y=x y=x对称:
∬ D f ( x , y ) d σ = { 2 ∬ D 1 f ( x , y ) d σ f ( x , y ) = f ( y , x ) 0 f ( x , y ) = − f ( y , x ) \iint_{D}f(x,y)d\sigma=\begin{cases} 2\iint_{D_1}f(x,y)d\sigma\ \ \ \ \ \ f(x,y)=f(y,x) \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f(x,y)=-f(y,x) \end{cases} ∬Df(x,y)dσ={2∬D1f(x,y)dσ f(x,y)=f(y,x)0 f(x,y)=−f(y,x)
其中 D 1 D_1 D1是 D D D关于 y = x y=x y=x对称的半个部分 - 轮换对称性:
在直角坐标系中,若将区域D中的x,y对调后,D不变,则有
I = ∬ D f ( x , y ) d x d y = ∬ D f ( y , x ) d x d y I = \iint_{D}f(x,y)dxdy=\iint_{D}f(y,x)dxdy I=∬Df(x,y)dxdy=∬Df(y,x)dxdy
不管积分区域对不对称,由于积分与变量名无关,因此天然有 ∬ D x y f ( x , y ) d x d y = ∬ D y x f ( y , x ) d y d x \iint_{D_{xy}}f(x,y)dxdy=\iint_{D_{yx}}f(y,x)dydx ∬Dxyf(x,y)dxdy=∬Dyxf(y,x)dydx。而这两个积分因为坐标系不一致,不可以做运算,而对称轮换性的原理是字母对调后再相加减很简单,因此若要让两个积分做运算,必然要有 D x y = D y x D_{xy}=D_{yx} Dxy=Dyx,因此需要积分区域D关于 y = x y=x y=x对称 - 二者区别:
- 积分函数的区别
- 普通对称性是对调之后若 f ( x , y ) = f ( y , x ) f(x,y)=f(y,x) f(x,y)=f(y,x)则为二倍,若 f ( x , y ) = − f ( y , x ) f(x,y)=-f(y,x) f(x,y)=−f(y,x)则为0
- 轮换对称性是对调之后 f ( x , y ) f(x,y) f(x,y)和 f ( y , x ) f(y,x) f(y,x)的关系并不重要,它俩表达式不一定一样。情况往往是二者表达式都比较复杂,但加起来比较简单,即 f ( x , y ) + f ( y , x ) = a f(x,y)+f(y,x)=a f(x,y)+f(y,x)=a
- 积分区域的区别
- 普通对称性的积分区域D关于 y = x y=x y=x对称
- 轮换对称性的积分区域满足的特征为:将 x , y x,y x,y对调后,积分区域D不变,这也需要区域D关于 y = x y=x y=x对称
- 整体来说,普通对称性中的关于 y = x y=x y=x对称的条件强度要比轮换对称性高得多。因为二者都要积分区域关于 y = x y=x y=x对称,前者还需要x、y对调后的函数之间有关系,而后者的满足条件就到此为止了。
- 积分函数的区别
- 举例:如下图就是轮换对称性

相关文章:

轮换对称性
二重积分 普通对称性–D关于 y x yx yx对称: ∬ D f ( x , y ) d σ { 2 ∬ D 1 f ( x , y ) d σ f ( x , y ) f ( y , x ) 0 f ( x , y ) − f ( y , x ) \iint_{D}f(x,y)d\sigma\begin{cases} 2\iint_{D_1}f(x,y)d\sigma\ \ \ \ \ \ f(x,y)f(y,x) \\ 0 \ \…...

【MySQL基础】--- 约束
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、什么…...
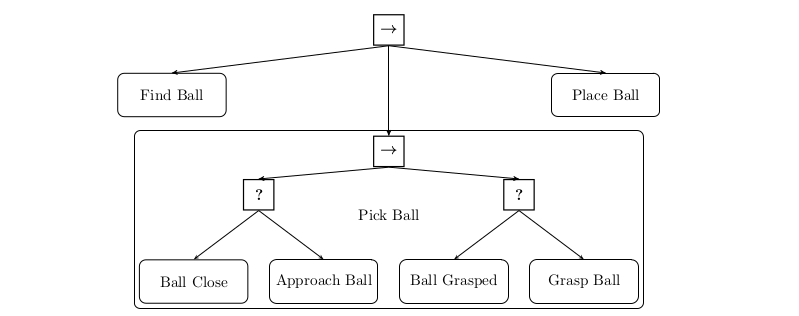
ROS2 的行为树 — 第 1 部分:解锁高级机器人决策和控制
一、说明 在复杂而迷人的机器人世界中,行为树(BT)已成为决策过程中不可或缺的一部分。它们提供了一种结构化、模块化和高效的方法来对机器人的行为进行编程。BT起源于视频游戏行业,用于控制非玩家角色,他们在机器人领域…...

kafka事务的详解
一 kafka事务的机制 1.1 kafka的事务机制 通过事务机制,KAFKA 可以实现对多个 topic 的多个 partition 的原子性的写入,即处于同一个事务内的所有消息,不管最终需要落地到哪个 topic 的哪个 partition, 最终结果都是要么全部写成功…...

Flutter Fair逻辑动态化架构设计与实现
本文的核心内容包括: 数据逻辑处理布局中的逻辑处理Flutter类型数据处理一、数据逻辑处理 我们接触的每一个Flutter界面,大多由布局和逻辑相关的代码组成。如Flutter初始工程的Counting Demo的代码: class _MyHomePageState extends State<MyHomePage> {// 变量 int…...
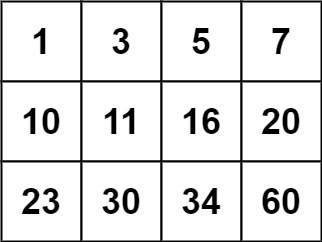
【每日一题】74. 搜索二维矩阵
74. 搜索二维矩阵 - 力扣(LeetCode) 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返…...
软件测试进大厂,拿高薪,怎么做?看这里!
有些同学大学专业不对口,但有想进大厂想拿高薪心,只要你有想法,那就一定有实现的方法。 俗话说:“世间无难事,只怕有心人”。仔细思索一下,哪家大厂能缺软件测试这一重要职位。相对大学所学专业而言&#…...

【读书笔记】基于世界500强的高薪实战Kubernetes课程
第1章 课程简介&&自我介绍 1-1 自我介绍 1-2 课程大纲内容介绍 1-3 课程更新通知 第2章 K8s必备知识-Docker容器基础入门 2-1 课程介绍 2-2 docker容器介绍 2-3 docker优缺点 2-4 安装和配置docker 2-5 修改内核参数 2-6 配置镜像加速器 2-7 配置常用镜像加…...

【Java 基础篇】Java并发包详解
多线程编程是Java开发中一个重要的方面,它能够提高程序的性能和响应能力。然而,多线程编程也伴随着一系列的挑战,如线程安全、死锁、性能问题等。为了解决这些问题,Java提供了一套强大的并发包。本文将详细介绍Java并发包的各个组…...
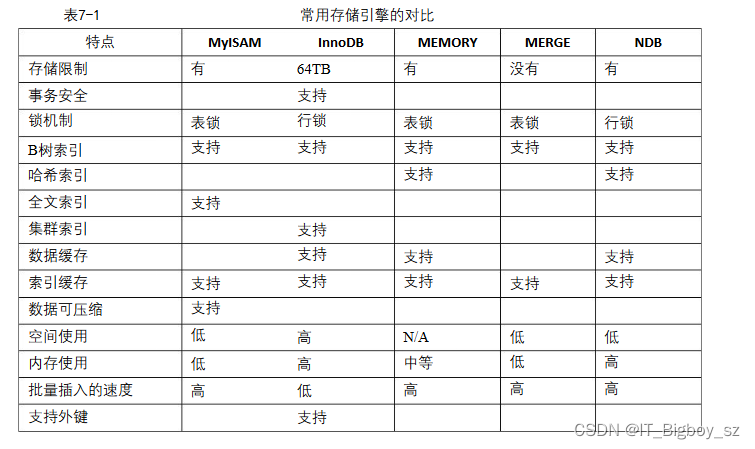
MYSQL存储引擎基础知识介绍
下面重点介绍几种常用的存储引擎,并对比各个存储引擎之间的区别,以帮助读者理解 不同存储引擎的使用方式。 MyISAM MyISAM是 MySQL的默认存储引擎。MyISAM不支持事务、也不支持外键,其优势是访 问的速度快,对事务完整性没有要求或者以 SEL…...

vue学习之element-ui组件集成
1. element-ui 链接 https://element.eleme.cn/#/zh-CN 2. element-ui 安装 cnpm install element-ui3. 创建项目 https://blog.csdn.net/qq_36940806/article/details/132921688?spm=1001.2014.3001.5502 4. 引入element库 /src/main.js 引入 element-uiimport Vue from…...

如何通过百度SEO优化提升网站排名(掌握基础概念,实现有效优化)
随着互联网的发展,搜索引擎优化(SEO)成为了网站优化中不可或缺的一部分。在中国,百度搜索引擎占据着主导地位,因此掌握百度SEO概念和优化技巧对网站的排名和曝光非常重要。 百度SEO排名的6个有效方法: 首…...

Golang 字符串
目录 1. Golang 字符串1.1. 基础概念1.2. 字符串编码1.3. 遍历字符串1.4. 类型转换1.5. 总结1.6. String Concatenation (字符串连接)1.6.1. Using the operator1.6.2. Using the operator1.6.3. Using the Join method1.6.4. Using Sprintf method1.6.5. Using Go string Bu…...

python应用中使用了multiprocessing多进程,使用pyinstaller打包出来的程序可能产生多个窗口
问题现象 我用pyside(类似pyqt)开发了一个应用程序。直接使用pycharm运行,一切都正常。但当我使用pyinstaller将它打包之后,再去运运行,发现窗口总是产生多个。 问题分析 直接运行没有问题,那么问题肯定…...
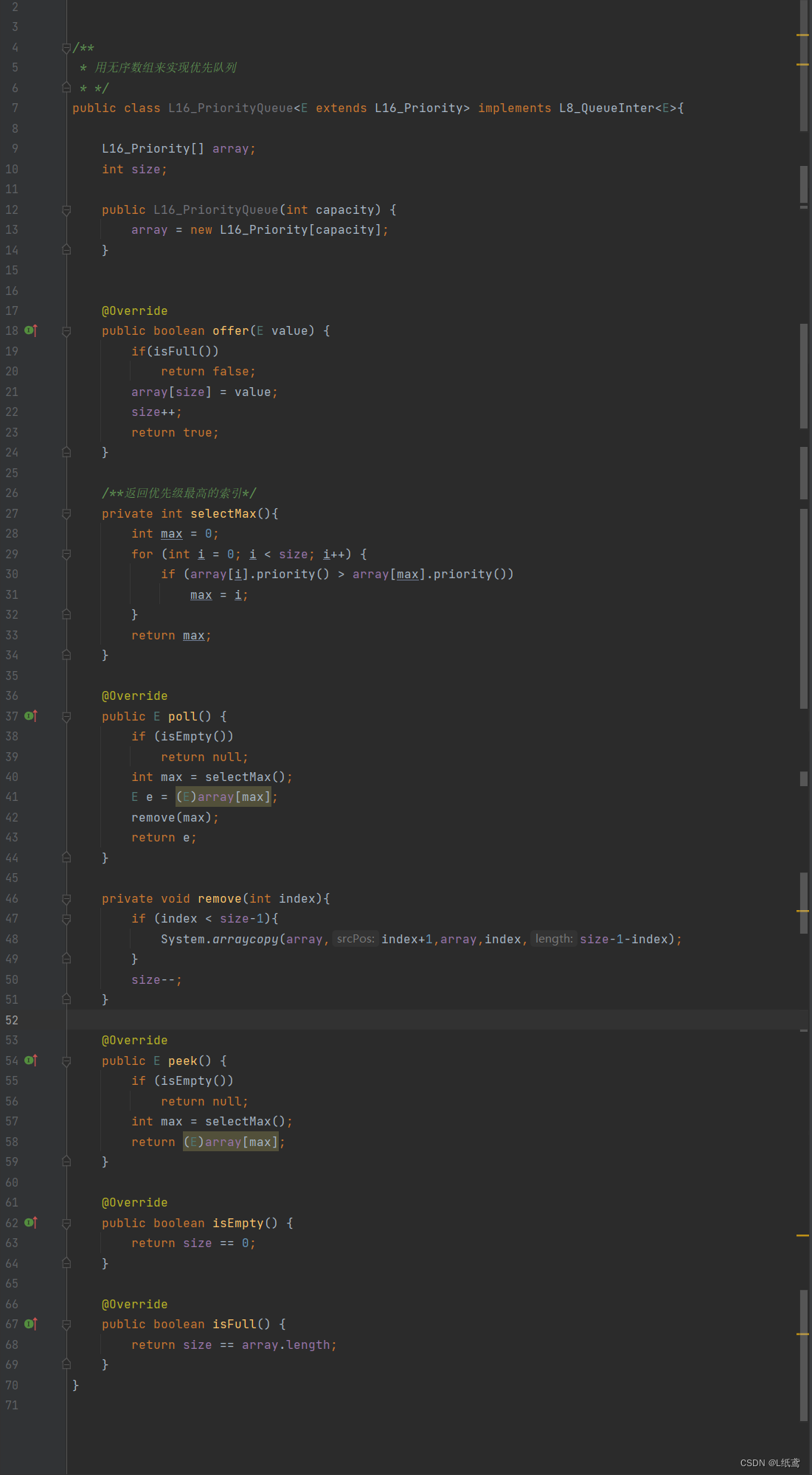
数据结构与算法——13.队列的拓展
这篇文章主要讲一下双端队列,优先队列,阻塞队列等队列的拓展内容。 目录 1.队列拓展概述 2.双端队列的链表实现 3.双端队列的数组实现 4.优先队列无序数组实现 5.阻塞队列 6.总结 1.队列拓展概述 首先来看一张图,来大致了解一下他们的…...
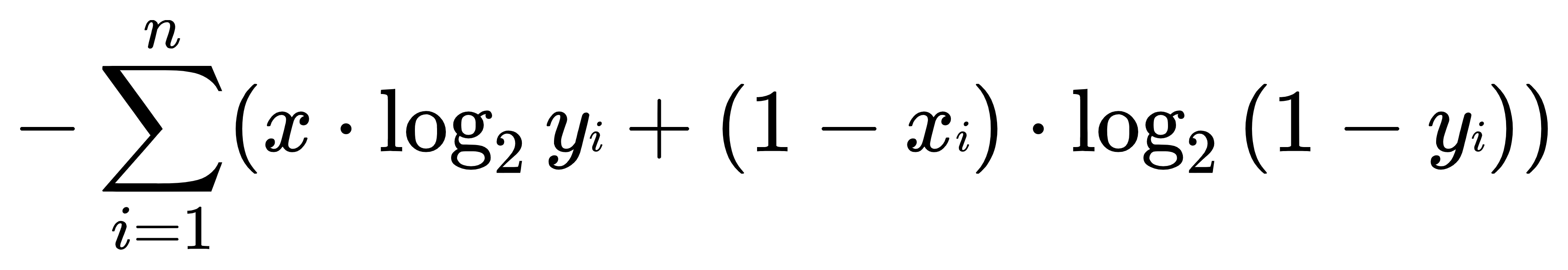
机器学习入门教学——损失函数(交叉熵法)
1、前言 我们在训练神经网络时,最常用到的方法就是梯度下降法。在了解梯度下降法前,我们需要了解什么是损失(代价)函数。所谓求的梯度,就是损失函数的梯度。如果不知道什么是梯度下降的,可以看一下这篇文章:机器学习入…...

pytest一些常见的插件
Pytest拥有丰富的插件架构,超过800个以上的外部插件和活跃的社区,在PyPI项目中以“ pytest- *”为标识。 本篇将列举github标星超过两百的一些插件进行实战演示。 插件库地址:http://plugincompat.herokuapp.com/ 1、pytest-html࿱…...

基于51单片机多路DTH11温湿度检测控制系统
一、系统方案 1、本设计采用51单片机作为主控器。 2、DHT11采集温度度,支持3路温度度,液晶1602显示。 3、按键设置报警阀值。 4、系统声光报警。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 //初始化LCD*********…...

宝塔重装注意事项
欢迎关注我的公众号:夜说猫,让一个贫穷的程序员不靠打代码也能吃饭~ 前言 宝塔8.0版本,宝塔卸载重装,或者重装Linux系统后重新安装宝塔也适用。 不能上来直接就执行安装宝塔脚本,除非之前没有安装过宝塔。 步骤 1、…...
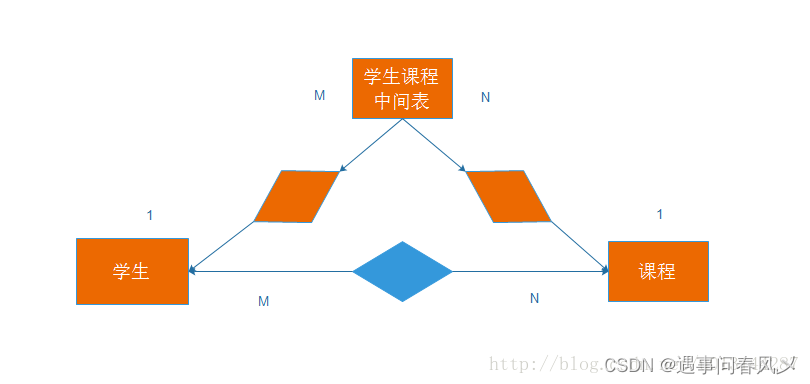
【MySQL】 MySQL的增删改查(进阶)--壹
文章目录 🛫数据库约束🌴约束类型🎋NOT NULL约束🎍UNIQUE:唯一约束🌳DEFAULT:默认值约束🎄PRIMARY KEY:主键约束🍀FOREIGN KEY:外键约束…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
