Xilinx FPGA未使用管脚上下拉状态配置(ISE和Vivado环境)
文章目录
- ISE开发环境
- Vivado开发环境
- 方式1:XDC文件约束
- 方式2:生成选项配置
ISE开发环境
ISE开发环境,可在如下Bit流文件生成选项中配置。
右键点击Generate Programming File,选择Process Properties,
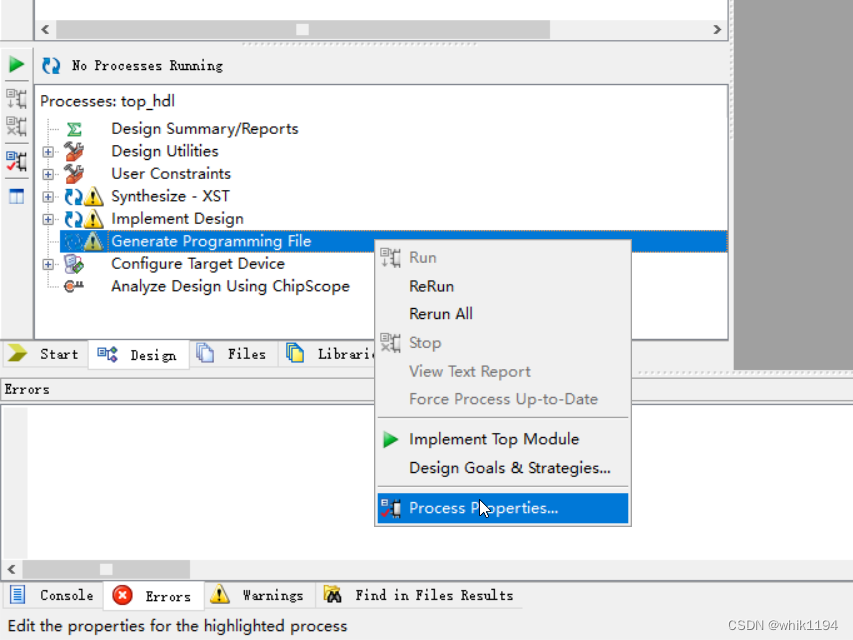
在弹出的窗口选择Configuration Options->Unused Pin,选择Pull Down、Pull Up或者Float。
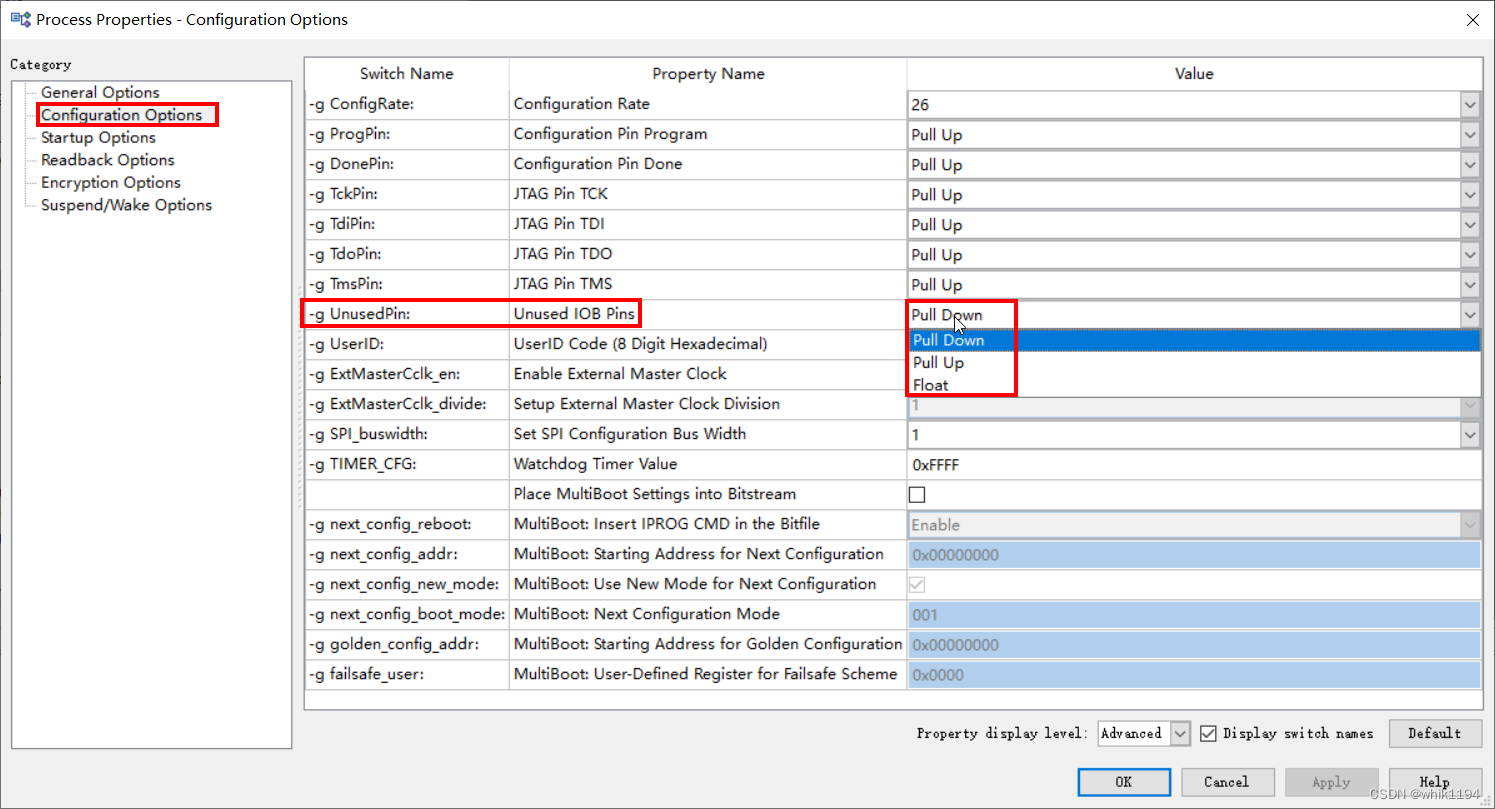
可以看到,除了未使用管脚,一些系统管脚,比如JTAG,Program、Done管脚等等都可以配置上下拉模式。
配置完成之后,重新生成Bit流文件即可。
Vivado开发环境
对于Vivado开发环境,共有两种方式可以设置未使用管脚的上下拉状态。
方式1:XDC文件约束
可以在XDC约束文件中根据需要添加以下约束语句,即可对未使用管脚电平状态进行设置:
#上拉
set_property BITSTREAM.CONFIG.UNUSEDPIN Pullup [current_design]
#下拉
set_property BITSTREAM.CONFIG.UNUSEDPIN Pulldown [current_design]
#悬空
set_property BITSTREAM.CONFIG.UNUSEDPIN Pullnone [current_design]
方式2:生成选项配置
在Generate Bitstrem右键,选择Bitstream Settings,点击图中蓝色字体
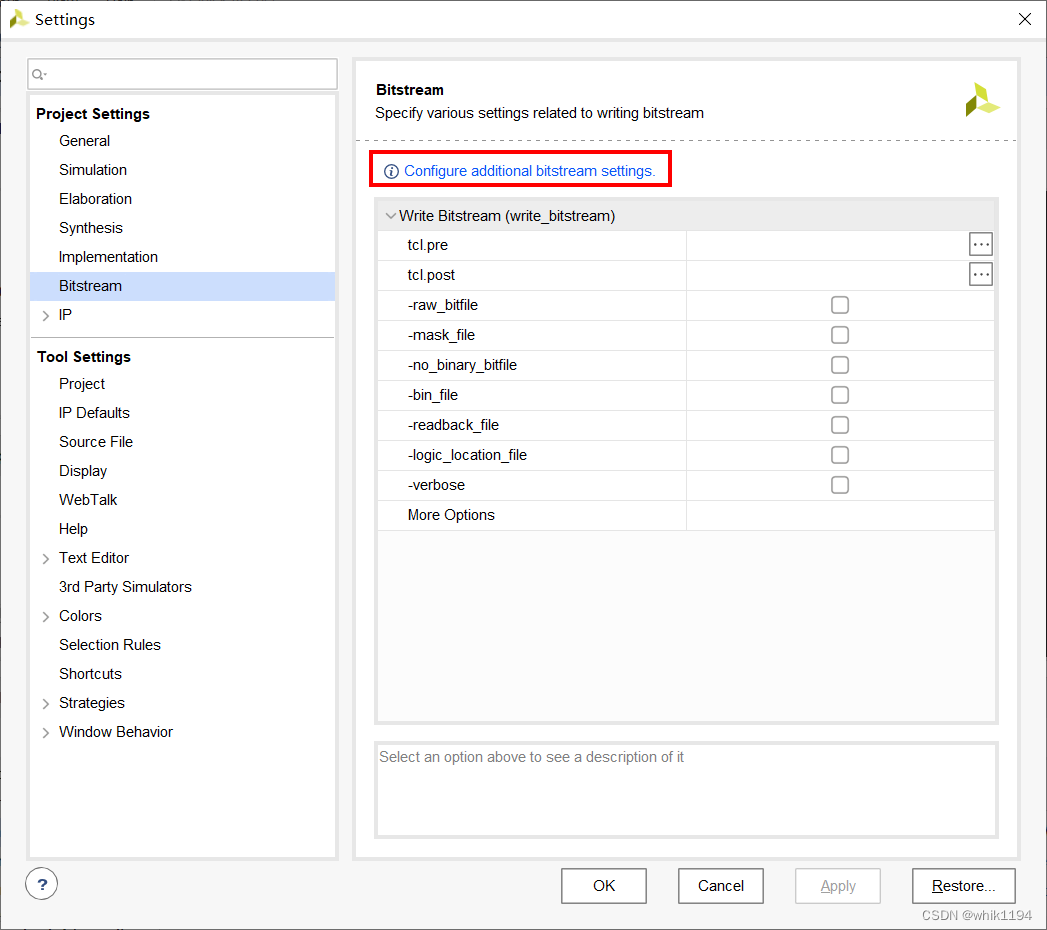
如果没有出现蓝色字体,需要先Open Implemented Design,之后就可以进行配置了。
选择Configuration,下拉找到系统管脚配置,选择自己所需要的上下拉状态。
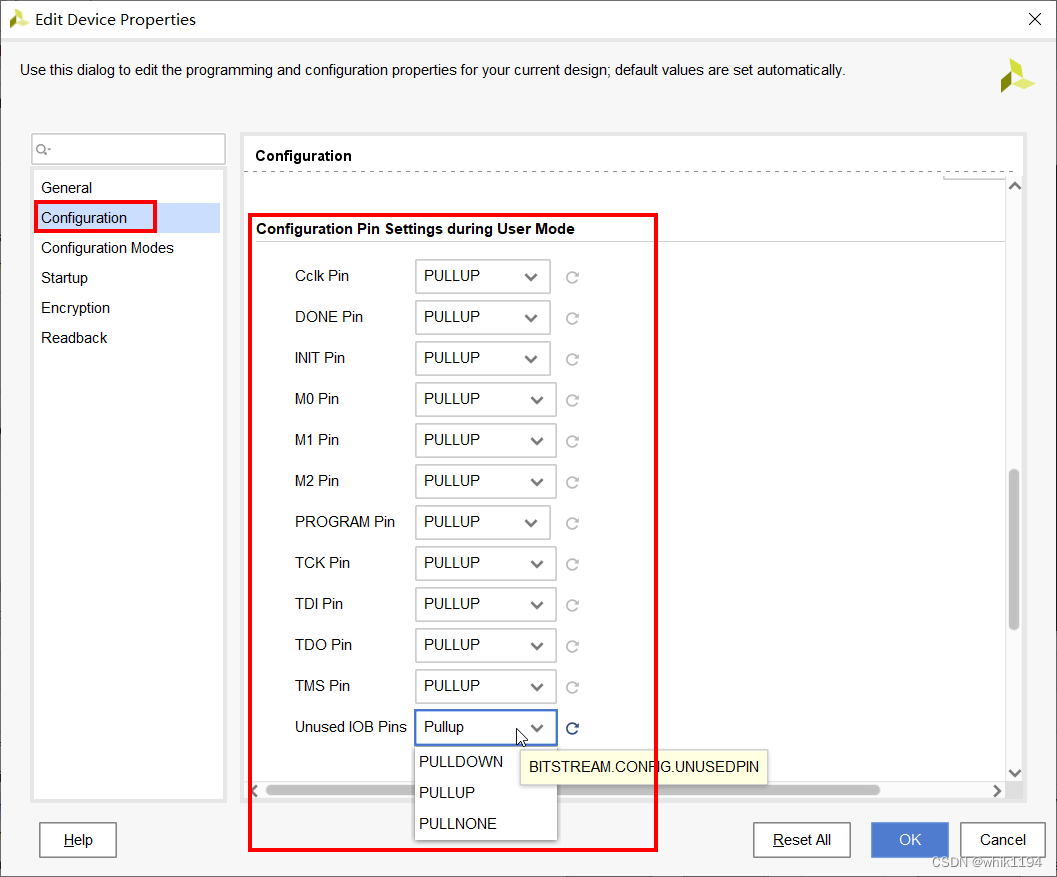
当把鼠标放在对应的选项时,会提示XDC约束语句的名称。
和ISE的生成选项配置类似,Vivado同样也可以配置JTAG管脚、Done、Prog等系统管脚的状态。
这两种配置方式的作用是一样,我更倾向于XDC文件约束的方式,方便在不同工程直接进行导入,设置完成之后,需要重新生成Bit流文件才能生效。
相关文章:

Xilinx FPGA未使用管脚上下拉状态配置(ISE和Vivado环境)
文章目录 ISE开发环境Vivado开发环境方式1:XDC文件约束方式2:生成选项配置 ISE开发环境 ISE开发环境,可在如下Bit流文件生成选项中配置。 右键点击Generate Programming File,选择Process Properties, 在弹出的窗口选…...
数据结构---链表(java)
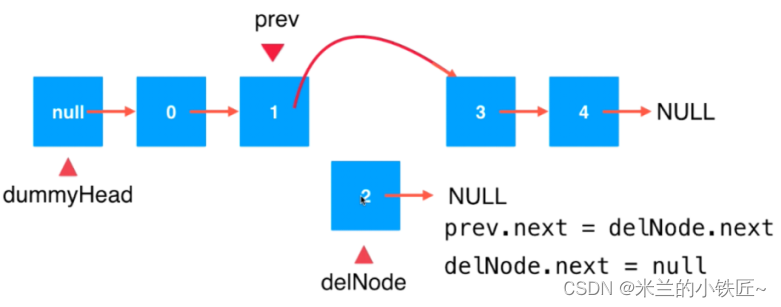
目录 1. 链表 2. 创建Node 3. 增加 4. 获取元素 5. 删除 6. 遍历链表 7. 查找元素是否存在 8. 链栈的实现 9. 链队的实现 1. 链表 数据存放在"Node"结点中 优点:不用考虑扩容和缩容的问题,实现了动态存储数据 缺点:没有…...
Qt --- Day02
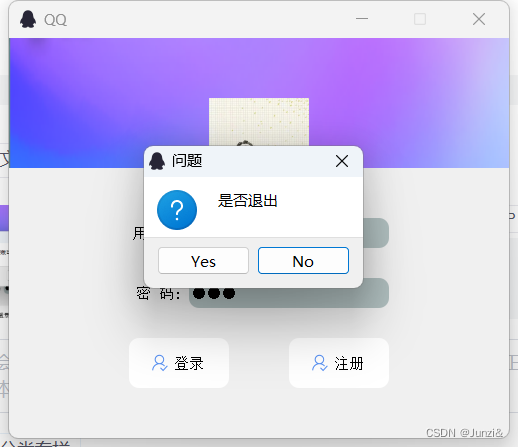
实现效果: 点击登录,检验用户密码是否正确,正确则弹出消息框,点击ok转到另一个页面 不正确跳出错误消息框,默认选线为Cancel,点击Yes继续登录 点击Cancel跳出问题消息框,默认选项No,…...
Redis 集合(Set)快速指南 | Navicat
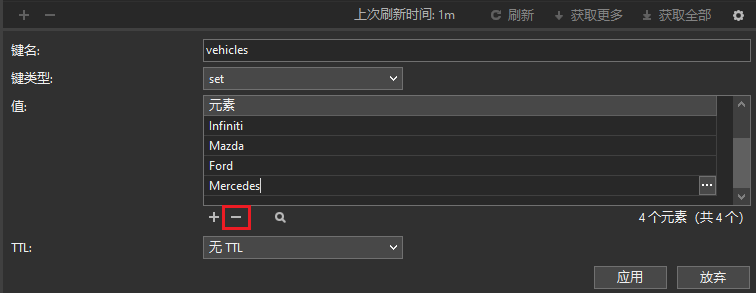
Redis 支持通过多种数据类型来存储项目集合。其中,包括列表、集合和哈希。上周的博文介绍了列表(List)数据类型并重点介绍了一些用于管理列表(List)的主要命令。在今天的文章中,我们将转向关注集合…...

【华为云云耀云服务器L实例评测】- 云原生实践,快捷部署人才招聘平台容器化技术方案!
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

【Java】泛型 之 什么是泛型
什么是泛型 泛型是一种“代码模板”,可以用一套代码套用各种类型。 在讲解什么是泛型之前,我们先观察Java标准库提供的ArrayList,它可以看作“可变长度”的数组,因为用起来比数组更方便。 实际上ArrayList内部就是一个Object[]…...
Python yaml 详解
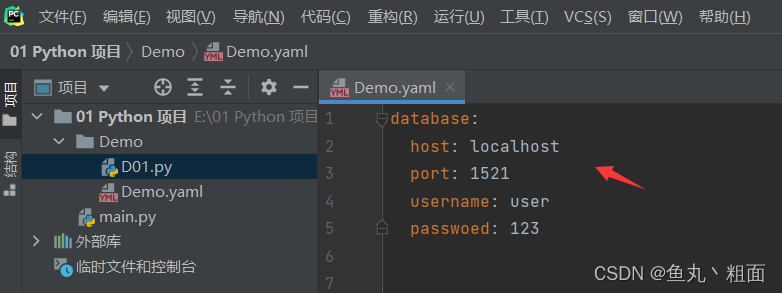
文章目录 1 概述1.1 特点1.2 导入 2 对象2.1 字典2.2 数组2.3 复合结构 3 操作3.1 读取3.2 写入 1 概述 1.1 特点 yaml 文件是一种数据序列化语言,广泛用于配置文件、日志文件等特点: ① 大小写敏感。② 使用缩进表示层级关系。缩进时不允许使用 Tab 键…...
-- 消费者消息确认)
RabbitMQ消息可靠性(二)-- 消费者消息确认
一、消费者消息确认是什么? 在这种机制下,消费者在接收到消息后,需要向 RabbitMQ 发送确认信息,告知 RabbitMQ 已经接收到该消息,并已经处理完毕。如果 RabbitMQ 没有接收到确认信息,则会将该消息重新加入…...

【python第7课 实例,类】
文章目录 一、实例1.1实例的变量1.2实例方法1.3 构造方法1.4析构函数1.4预置实例属性: 二,类1.1类变量1.2类方法1.3静态方法1.4类属性的增删改查 一、实例 1.1实例的变量 使用示例 class dog:def __init__(self,k,c,a):self.kinds kself.color csel…...
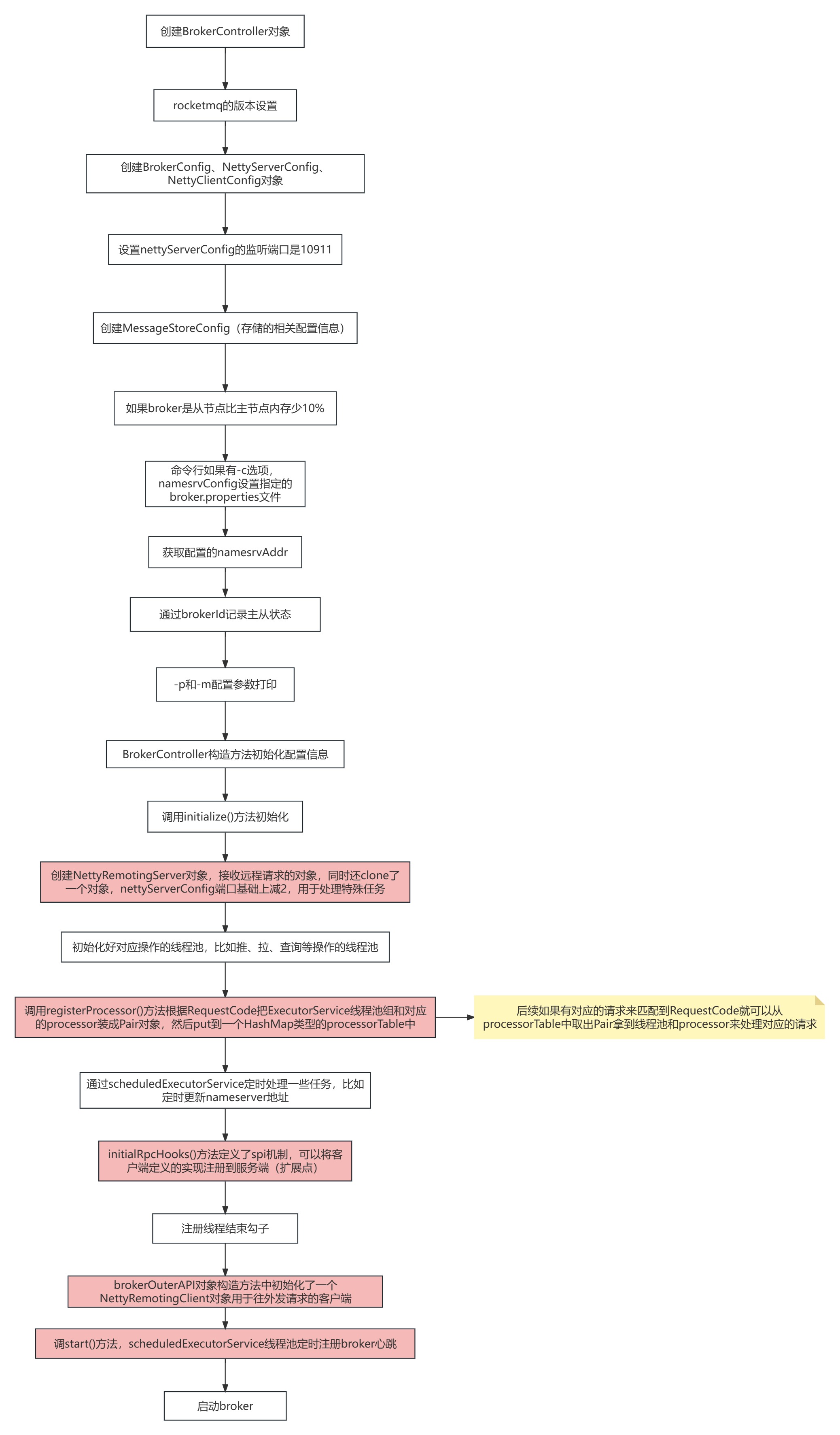
RocketMQ源码解析(上)
一、ACL权限控制 应用场景: RocketMQ提供了针对队列、用户等不同维度的非常全面的权限管理机制。通常来说,RocketMQ作为一个内部服务,是不需要进行权限控制的,但是,如果要通过RocketMQ进行跨部门甚至跨公司的合作&…...
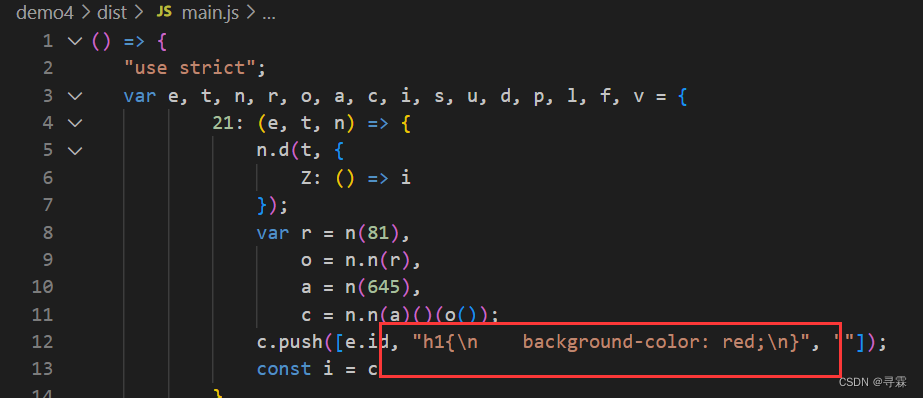
Webpack打包CSS文件,解决You may need an appropriate loader to handle this file type报错
在项目文件夹下创建webpack.config.js文件,该文件就是Webpack的配置文件 注意:该文件中遵循Node.js的代码格式规范 ,需要对导出配置文件中的内容 Webpack在默认情况下只能打包js文件,如果我们希望他能够打包其他类型的文件&#…...

轮换对称性
二重积分 普通对称性–D关于 y x yx yx对称: ∬ D f ( x , y ) d σ { 2 ∬ D 1 f ( x , y ) d σ f ( x , y ) f ( y , x ) 0 f ( x , y ) − f ( y , x ) \iint_{D}f(x,y)d\sigma\begin{cases} 2\iint_{D_1}f(x,y)d\sigma\ \ \ \ \ \ f(x,y)f(y,x) \\ 0 \ \…...

【MySQL基础】--- 约束
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、什么…...
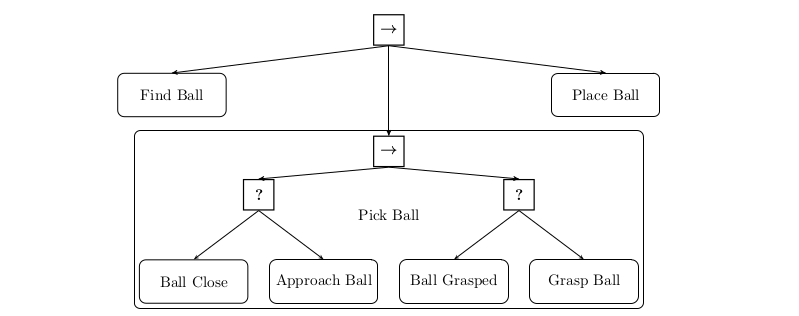
ROS2 的行为树 — 第 1 部分:解锁高级机器人决策和控制
一、说明 在复杂而迷人的机器人世界中,行为树(BT)已成为决策过程中不可或缺的一部分。它们提供了一种结构化、模块化和高效的方法来对机器人的行为进行编程。BT起源于视频游戏行业,用于控制非玩家角色,他们在机器人领域…...

kafka事务的详解
一 kafka事务的机制 1.1 kafka的事务机制 通过事务机制,KAFKA 可以实现对多个 topic 的多个 partition 的原子性的写入,即处于同一个事务内的所有消息,不管最终需要落地到哪个 topic 的哪个 partition, 最终结果都是要么全部写成功…...

Flutter Fair逻辑动态化架构设计与实现
本文的核心内容包括: 数据逻辑处理布局中的逻辑处理Flutter类型数据处理一、数据逻辑处理 我们接触的每一个Flutter界面,大多由布局和逻辑相关的代码组成。如Flutter初始工程的Counting Demo的代码: class _MyHomePageState extends State<MyHomePage> {// 变量 int…...
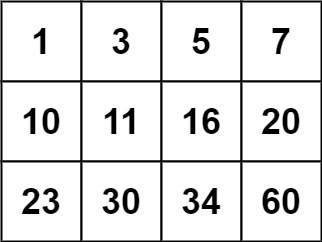
【每日一题】74. 搜索二维矩阵
74. 搜索二维矩阵 - 力扣(LeetCode) 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返…...
软件测试进大厂,拿高薪,怎么做?看这里!
有些同学大学专业不对口,但有想进大厂想拿高薪心,只要你有想法,那就一定有实现的方法。 俗话说:“世间无难事,只怕有心人”。仔细思索一下,哪家大厂能缺软件测试这一重要职位。相对大学所学专业而言&#…...

【读书笔记】基于世界500强的高薪实战Kubernetes课程
第1章 课程简介&&自我介绍 1-1 自我介绍 1-2 课程大纲内容介绍 1-3 课程更新通知 第2章 K8s必备知识-Docker容器基础入门 2-1 课程介绍 2-2 docker容器介绍 2-3 docker优缺点 2-4 安装和配置docker 2-5 修改内核参数 2-6 配置镜像加速器 2-7 配置常用镜像加…...

【Java 基础篇】Java并发包详解
多线程编程是Java开发中一个重要的方面,它能够提高程序的性能和响应能力。然而,多线程编程也伴随着一系列的挑战,如线程安全、死锁、性能问题等。为了解决这些问题,Java提供了一套强大的并发包。本文将详细介绍Java并发包的各个组…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
