【动态规划刷题 16】最长等差数列 (有难度) 等差数列划分 II - 子序列
1027. 最长等差数列
https://leetcode.cn/problems/longest-arithmetic-subsequence/
给你一个整数数组 nums,返回 nums 中最长等差子序列的长度。
回想一下,nums 的子序列是一个列表 nums[i1], nums[i2], …, nums[ik] ,且 0 <= i1 < i2 < … < ik <= nums.length - 1。并且如果 seq[i+1] - seq[i]( 0 <= i < seq.length - 1) 的值都相同,那么序列 seq 是等差的。
示例 1:
输入:nums = [3,6,9,12]
输出:4
解释:
整个数组是公差为 3 的等差数列。
示例 2:
输入:nums = [9,4,7,2,10]
输出:3
解释:
最长的等差子序列是 [4,7,10]。
示例 3:
输入:nums = [20,1,15,3,10,5,8]
输出:4
解释:
最长的等差子序列是 [20,15,10,5]。
1.状态表示*
我们先试着定义一个状态转移数组:
dp[i] 表⽰:以 i 位置元素为结尾的「所有⼦序列」中,最⻓的等差序列的⻓度。
但是这⾥有⼀个⾮常致命的问题,那就是我们⽆法确定 i 结尾的等差序列的样⼦。这样就会导致我们⽆法推导状态转移⽅程,因此我们定义的状态表⽰需要能够确定⼀个等差序列:
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,最⻓的等差序列的⻓度。
2.状态转移方程
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * b - c 。我们
根据 a 的情况讨论:
- a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓等差序列的⻓度,然后再加上 j 位置的元素即可。于是
dp[i][j] = dp[k][i] +1。这⾥因为会有许多个 k ,我们仅需离 i 最近的 k 即可。因此任何最⻓的都可以以 k 为结尾; - a 存在,但是 b < a < c :此时只能两个元素⾃⼰玩了, dp[i][j] = 2 ;
- a 不存在:此时依旧只能两个元素⾃⼰玩了, dp[i][j] = 2 ;
优化:
⼀边 dp ,⼀边保存。这种⽅式,我们仅需保存最近的元素的下标,不⽤保存下标数组。但是⽤这种⽅法的话,我们在遍历顺序那⾥,先固定倒数第⼆个数,再遍历倒数第⼀个数。这样就可以在 i 使⽤完时候,将 nums[i] 扔到哈希表中。
3. 初始化
根据实际情况,可以将所有位置初始化为 2 。
4. 填表顺序
a. 先固定倒数第⼆个数;
b. 然后枚举倒数第⼀个数。
5. 返回值
由于不知道最⻓的结尾在哪⾥,因此返回 dp 表中的最⼤值。
代码:
int longestArithSeqLength(vector<int>& nums) {int n=nums.size();unordered_map<int,int> hash;hash[nums[0]]=0;//表示的是以 i,j 为结尾的,最长的等差子序列的长度int Max=2;vector<vector<int>> dp(n,vector<int>(n,2));for(int i=0;i<n;i++)//先固定倒数第二个位置{for(int j=i+1;j<n;j++)//在固定倒数第一个位置{int a=2*nums[i]-nums[j];if(hash.count(a)&&hash[a]<i)dp[i][j]=dp[hash[a]][i]+1;Max=max(Max,dp[i][j]);}hash[nums[i]]=i;}return Max;}
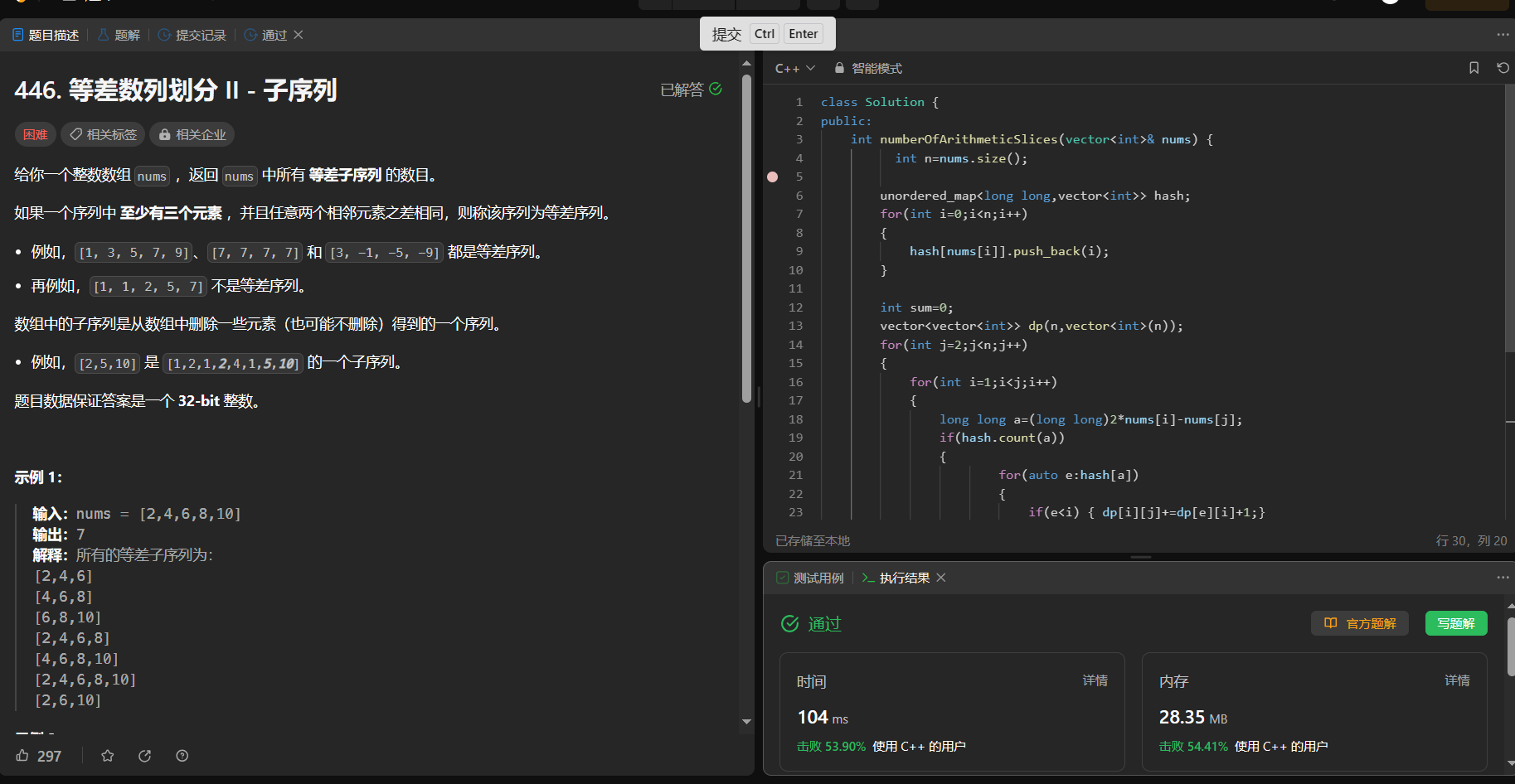
446. 等差数列划分 II - 子序列
https://leetcode.cn/problems/arithmetic-slices-ii-subsequence/
给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
例如,[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。
再例如,[1, 1, 2, 5, 7] 不是等差序列。
数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
例如,[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
题目数据保证答案是一个 32-bit 整数。
示例 1:
输入:nums = [2,4,6,8,10]
输出:7
解释:所有的等差子序列为:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
示例 2:
输入:nums = [7,7,7,7,7]
输出:16
解释:数组中的任意子序列都是等差子序列。
1.状态表示*
我们先试着定义一个状态转移数组:
dp[i] 表⽰:以 i 位置元素为结尾的「所有⼦序列」中,最⻓的等差序列的⻓度。
但是这⾥有⼀个⾮常致命的问题,那就是我们⽆法确定 i 结尾的等差序列的样⼦。这样就会导致我们⽆法推导状态转移⽅程,因此我们定义的状态表⽰需要能够确定⼀个等差序列:
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,等差⼦序列的个数。
2.状态转移方程
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * b - c 。我们
根据 a 的情况讨论:
- a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓等差序列的⻓度,然后再加上 j 位置的元素即可。于是
dp[i][j] = dp[k][i] +1。这⾥因为会有许多个 k ,我们仅需离 i 最近的 k 即可。因此任何最⻓的都可以以 k 为结尾; - b. 因为 a 可能有很多个,我们需要全部累加起来
综上, dp[i][j] += dp[k][i] + 1 。
优化:
优化点:我们发现,在状态转移⽅程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之前,将
所有元素 +下标数组绑定在⼀起,放到哈希表中。这⾥为何要保存下标数组,是因为我们要统计个
数,所有的下标都需要统计。
3. 初始化
刚开始是没有等差数列的,因此初始化 dp 表为 0
4. 填表顺序
a. 先固定倒数第⼆个数;
b. 然后枚举倒数第⼀个数。
5. 返回值
我们要统计所有的等差⼦序列,因此返回 dp 表中所有元素的和。
代码:
int numberOfArithmeticSlices(vector<int>& nums) {int n=nums.size();unordered_map<long long,vector<int>> hash;for(int i=0;i<n;i++){hash[nums[i]].push_back(i);}int sum=0;vector<vector<int>> dp(n,vector<int>(n));for(int j=2;j<n;j++){for(int i=1;i<j;i++){long long a=(long long)2*nums[i]-nums[j];if(hash.count(a)){for(auto e:hash[a]){if(e<i) { dp[i][j]+=dp[e][i]+1;}else break;}}sum+=dp[i][j];}}return sum;}
相关文章:

【动态规划刷题 16】最长等差数列 (有难度) 等差数列划分 II - 子序列
1027. 最长等差数列 https://leetcode.cn/problems/longest-arithmetic-subsequence/ 给你一个整数数组 nums,返回 nums 中最长等差子序列的长度。 回想一下,nums 的子序列是一个列表 nums[i1], nums[i2], …, nums[ik] ,且 0 < i1 <…...
【postgresql】替换 mysql 中的ifnull()
数据库由mysql 迁移到postgresql,程序在执行查询时候报错。 HINT: No function matches the given name and argument types. You might need to add explicit type casts. CONTEXT: referenced column: ifnull 具体SQL: SELECT ifnull(phone,) FROM c_user p…...
)
单例模式(懒汉式,饿汉式,变体)
单例模式,用于确保一个类只有一个实例,并提供一个全局访问点以访问该实例。 饿汉式(Eager Initialization) 程序启动时就创建实例 #include <iostream> class SingletonEager { private:static SingletonEager* instanc…...

Java Lambda表达式:简洁且强大的函数式编程工具
Lambda表达式是Java 8及以后版本中引入的一种函数式编程特性。它是一种匿名函数,允许开发人员以简洁和易读的方式编写代码,并且可以作为参数传递给方法或存储在变量中。Lambda表达式的基本语法如下:(parameters) -> expression,…...
开源框架中的责任链模式实践
作者:vivo 互联网服务器团队-Wang Zhi 责任链模式作为常用的设计模式而被大家熟知和使用。本文介绍责任链的常见实现方式,并结合开源框架如Dubbo、Sentinel等进行延伸探讨。 一、责任链介绍 在GoF 的《设计模式》一书中对责任链模定义的:将…...
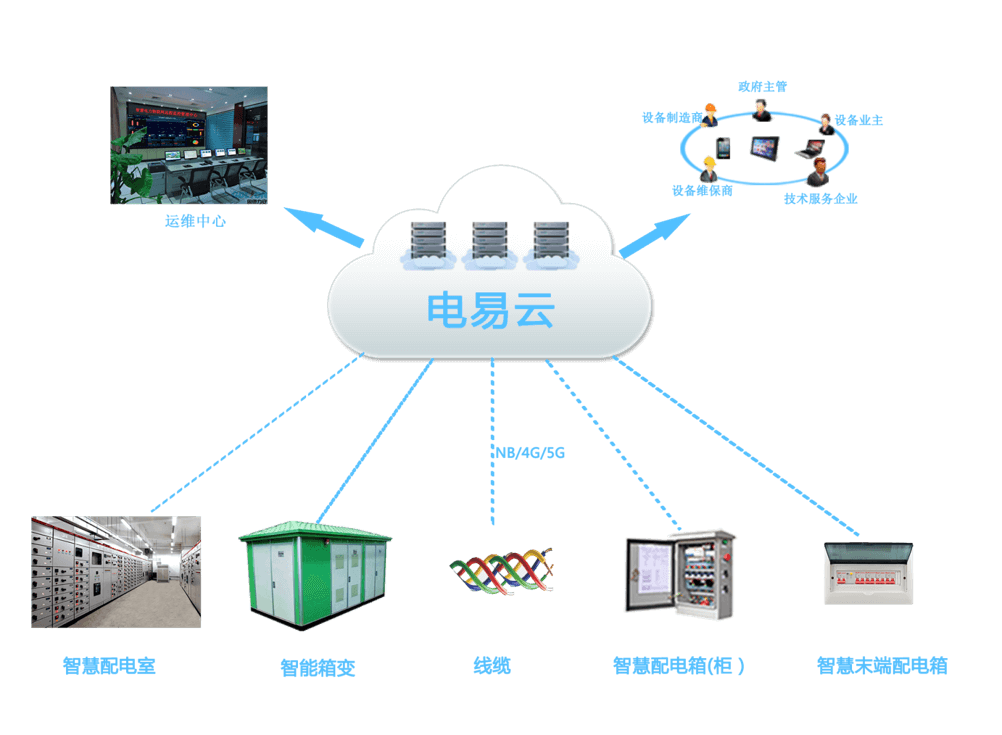
智能配电系统:保障电力运行安全、可控与高效
智能配电系统是一种先进的电力分配技术,它通过智能化、数字化和网络化等方式,有效地保障了电力运行的安全、可控和高效。 力安科技智能配电系统是在配电室(含高压柜、变压器、低压柜)、箱式变电站、配电箱及动力柜(…...
-每天学习10个知识)
MySQL学习系列(11)-每天学习10个知识
目录 1. 数据库设计的关键因素2. 使用存储过程和函数来提高性能和可重用性3. MySQL性能优化4. 使用视图简化查询和提供数据安全性5. 数据库备份和恢复策略的重要性和实践经验6. 在分布式系统中保证数据一致性和可用性7. 理解MySQL的复制和其在实际应用中的作用8. 使用游标进行分…...
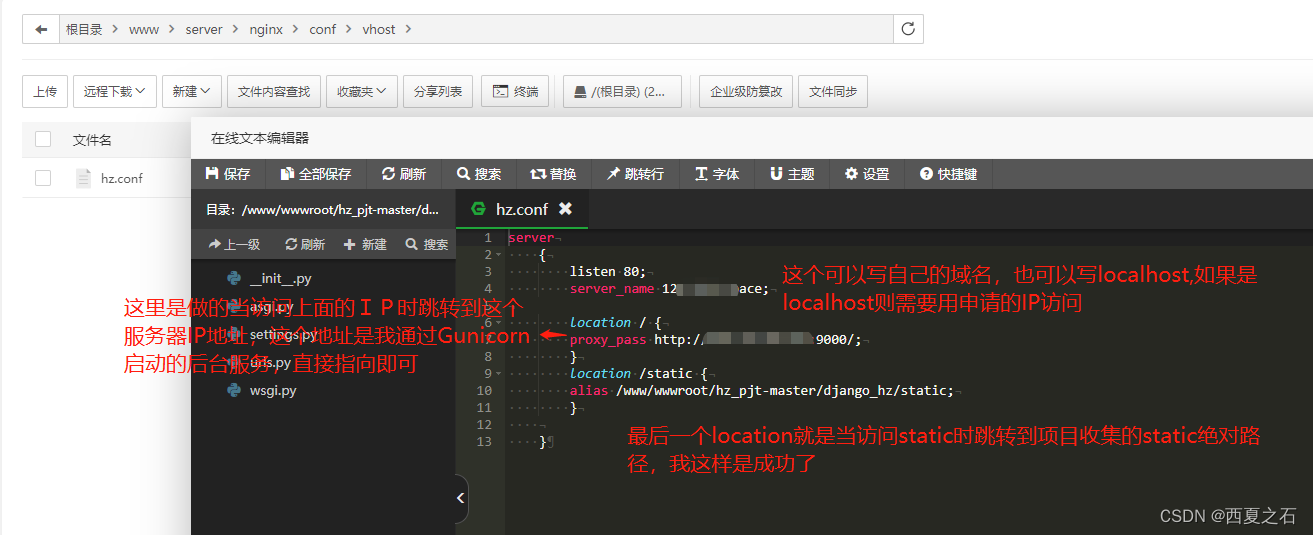
如何通过Gunicorn和Niginx部署Django
本文主要介绍如何配置Niginx加载Django的静态资源文件,也就是Static 1、首先需要将Django项目中的Settings.py 文件中的两个参数做以下设置: STATIC_URL /static/ STATIC_ROOT os.path.join(BASE_DIR, static) 然后在宝塔面板中执行python manage.…...
C语言 cortex-A7核UART总线实验
一、C 1)uart4.h #ifndef __UART4_H__ #define __UART4_H__ #include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h&quo…...

asp.net C#免费反编译工具ILSpy
在维护一个没有源码的C#项目,只能反编译了。 项目主页 https://github.com/icsharpcode/ILSpy 使用方法 中文界面使用简单,把你要反编译的dll拖过去就可以了。好使!!!...

演讲实录:DataFun 垂直开发者社区基于指标平台自主洞察北极星指标
在7月14日举办的 Kyligence 用户大会的数智新应用论坛上,DataFun COO 杜颖女士为大家带来了《垂直开发者社区基于指标平台自主洞察北极星指标》的主题演讲。接下来,我们一起看看 DataFun 如何在没有专门的 IT 团队的情况下,实现对北极星指标的…...
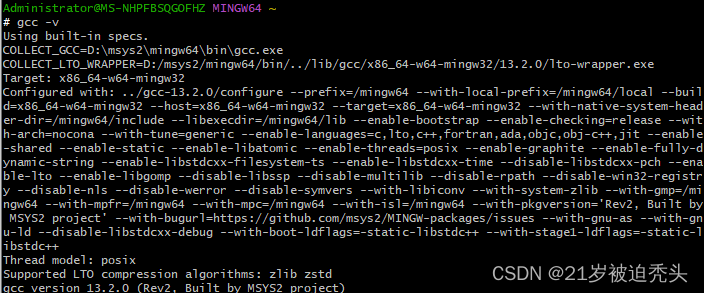
ffmpeg编译 Error: operand type mismatch for `shr‘
错误如下: D:\msys2\tmp\ccUxvBjQ.s: Assembler messages: D:\msys2\tmp\ccUxvBjQ.s:345: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:410: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:470: Error: operand type mismatch…...
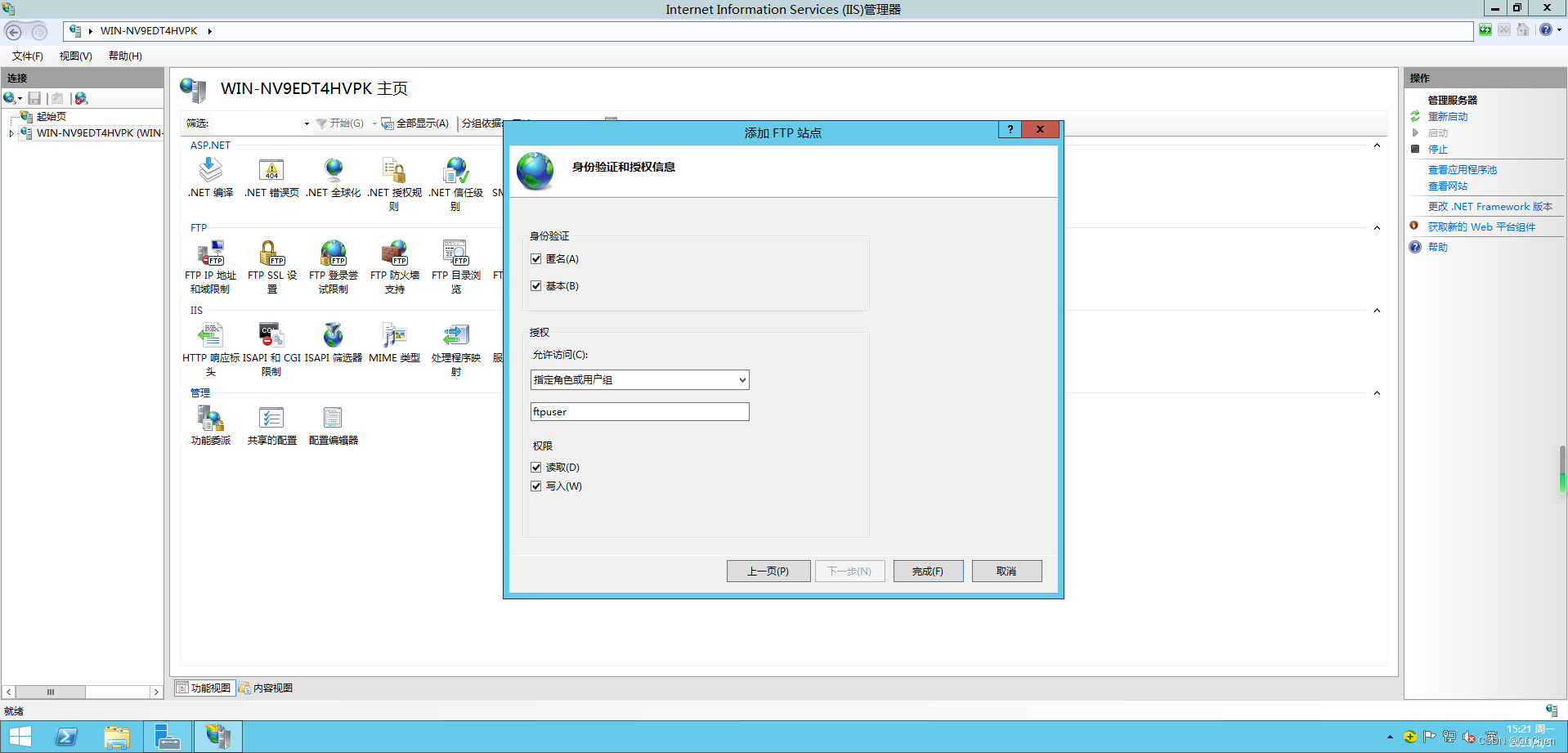
【Windows Server 2012 R2搭建FTP站点】
打开服务器管理器——添加角色和功能 下一步 下一步 下一步 选择FTP服务器,勾上FTP服务和FTP扩展,点击下一步 安装 安装完成关闭 打开我们的IIS服务器 在WIN-XXX主页可以看到我们的FTP相关菜单 右键WIN-XXXX主页,添加FTP站点 输入站点名称-FT…...

python教程:使用gevent实现高并发并限制最大并发数
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 import time import gevent from gevent.pool import Pool from gevent import monkey # 一,定义最大并发数 p Pool(20) # 二,导入gevent…...

借助reCAPTCHA实现JavaScript验证码功能
前言 验证码(CAPTCHA)是一种常见的安全验证机制,常用于区分真实用户和机器人。使用验证码可以有效防止恶意登录、自动注册或者密码爆破等攻击。本文将借助reCAPTCHA第三方库来实现JavaScript验证码功能。 验证码的原理 验证码的核心思想是要…...
监控数据的采集方式及原理
采集方法使用频率从高到低依次是读取 /proc目录、执行命令行工具、远程黑盒探测、拉取特定协议的数据、连接到目标对象执行命令、代码埋点、日志解析。 读取 /proc目录 /proc是一个位于内存中的伪文件系统,而在该目录下保存的不是真正的文件和目录,而是…...

Vue路由与node.js环境搭建
目录 前言 一.Vue路由 1.什么是spa 1.1简介 1.2 spa的特点 1.3 spa的优势以及未来的挑战 2.路由的使用 2.1 导入JS依赖 2.2 定义两个组件 2.3 定义组件与路径对应关系 2.4 通过路由关系获取路由对象 2.5 将对象挂载到vue实例中 2.6 定义触发路由事件的按钮 2.7 定…...
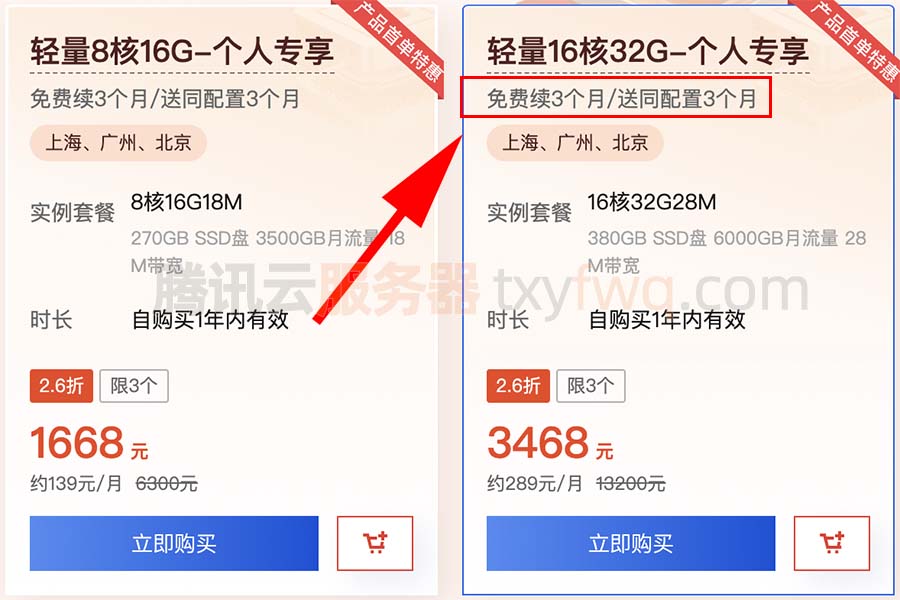
腾讯云16核服务器性能测评_轻量和CVM配置大全
腾讯云16核服务器配置大全,CVM云服务器可选择标准型S6、标准型SA3、计算型C6或标准型S5等,目前标准型S5云服务器有优惠活动,性价比高,计算型C6云服务器16核性能更高,轻量16核32G28M带宽优惠价3468元15个月,…...
Postman应用——下载注册和登录
文章目录 下载安装注册登录注册账号登录账号 下载安装 Postman下载:https://www.postman.com/ 访问链接后,进入首页,根据自己的操作系统下载对应的版本。 找到下载到的目录直接双击.exe文件,会默认安装在C盘,安装完会…...

uni-app混合开发 navigateTo、reLaunch、redirectTo、switchTab区别
1.navigateTo 保留当前页面,跳转到应用内的某个页面,使用uni.navigateBack可以返回到原页面。 要注意的是navigateTo只能跳转的应用内非 tabBar 的页面的路径 , 路径后可以带参数;如果跳转url参数为tabBar的路径则无法进行跳转 2.redir…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
