计算物理专题----随机游走实战
- 计算物理专题----随机游走实战
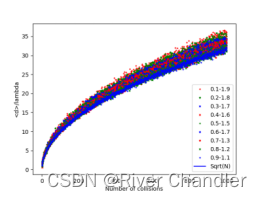
Problem 1 Implement the 3D random walk
| 拟合线 | ||||
 |  |  | ||
|
|
|
| ||
| 自旋的 拟合函数(没有数学意义) | 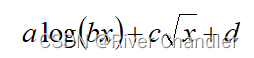 | 参数:0.627,3.336,0.603,-3.234 | ||
- 自由程满足在一定范围内的均匀分布
- 以标准自由程为单位长度,可得到均匀分布的统计特征
- 方均根距离与平均自由程的比值满足
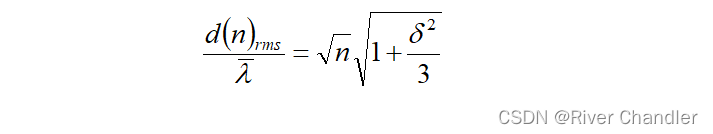
P1-a.py
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt# 设置实验参数
Lambda = 1
Collision = 1000
np.random.seed(2)
New = np.zeros(Collision)
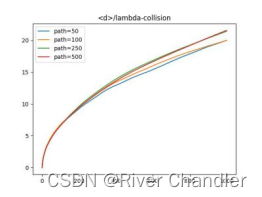
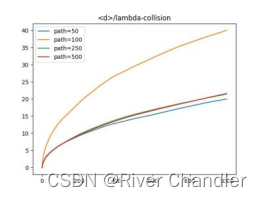
Path = 500def mc_experiment():global Lambdaglobal Collisionglobal NewLocation = np.zeros((Collision,3))d = np.zeros(Collision)for i in range(1,Collision):theta = np.random.uniform(0,np.pi)phi = np.random.uniform(0,2*np.pi)Location[i] = Location[i-1] + np.array([Lambda*np.sin(theta)*np.cos(phi),\Lambda*np.sin(theta)*np.sin(phi),\Lambda*np.cos(theta)])Dis = np.array([sum(i**2)**0.5 for i in Location])for i in range(Collision):d[i] = (sum(Dis[:i]**2)/(i+1))**0.5New[i] += d[i]/Path#plt.plot(range(Collision),d/Lambda)return Locationfor i in range(Path):l = mc_experiment()print(i)if i==49:plt.plot(range(Collision),New/Lambda*10,label="path=50")if i==99:plt.plot(range(Collision),New/Lambda*5,label="path=100")if i==249:plt.plot(range(Collision),New/Lambda*2,label="path=250")if i==499:plt.plot(range(Collision),New/Lambda,label="path=500")plt.legend()
plt.title("<d>/lambda-collision")
plt.pause(0.01)
plt.savefig("1-a.jpg")P1-b.py
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pickle# 设置实验参数
exceed = 0.1
Collision = 1000
np.random.seed(2)
New = np.zeros(Collision)
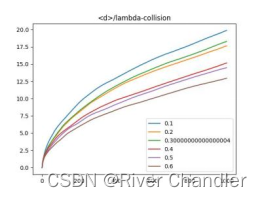
Path = 50def mc_experiment():global Lambdaglobal Collisionglobal Newglobal exceedLocation = np.zeros((Collision,3))d = np.zeros(Collision)for i in range(1,Collision):theta = np.random.uniform(0,np.pi)phi = np.random.uniform(0,2*np.pi)Lambda = np.random.uniform(1-exceed,1+exceed)Location[i] = Location[i-1] + np.array([Lambda*np.sin(theta)*np.cos(phi),\Lambda*np.sin(theta)*np.sin(phi),\Lambda*np.cos(theta)])Dis = np.array([sum(i**2)**0.5 for i in Location])for i in range(Collision):d[i] = (sum(Dis[:i]**2)/(i+1))**0.5New[i] += d[i]/Path#plt.plot(range(Collision),d/Lambda)for j in range(6):for i in range(Path):mc_experiment()print(j,":",i)plt.plot(range(Collision),New/(1+exceed),label=str(exceed))f = open("./"+str(j)+".txt",'wb')pickle.dump(New,f)f.close()New = np.zeros(Collision)exceed += 0.1plt.legend()
plt.title("<d>/lambda-collision")
plt.pause(0.01)
plt.savefig("1-b.jpg")P1-c.py
import pickleData = []
for i in range(6):f = open("./"+str(i)+".txt",'rb')Data.append(pickle.load(f))import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt#确定你想要的函数
def func(x,a,b,c,d):return a * np.log(b*x) + c * x**0.5 + dx_data = np.array(range(len(Data[0])))[1:]
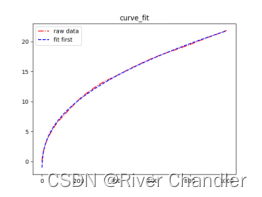
y_data = Data[0][1:]plt.title("curve_fit")
plt.plot(x_data,y_data,"r-.",label="raw data")popt,pcov = curve_fit(func,x_data,y_data)
plt.plot(x_data,func(x_data,*popt),"b--",label="fit first")
plt.legend()
plt.pause(0.01)
plt.savefig("1-c")
print("popt 1",end=" ")
print(popt)
print("pcov 1")
print(pcov)
P-M-1.py
import numpy as np
import matplotlib.pyplot as pltlamda=1 #平均自由程-步长
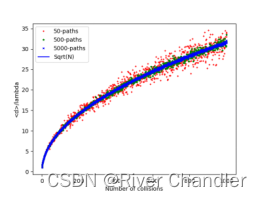
N=1000 #总步数,即每次实验走N步t = [i for i in range(1,N+1)]def drms(m):drms=[]#计算均方根距离: for i in range(1,N+1,1): #3d-球坐标系,利用角参数\thata,\phi 描述其移动,走N步r=np.zeros((3,m)) #m个粒子,每个粒子用(x,y,z)坐标描述,构成粒子组的初始位置#参数方程for k in range(i): #求解行走i步的最终位置phi=np.random.uniform(0,2*np.pi,m) #生成m个随机数costheta=np.random.uniform(-1,1,m) #生成m个随机数r[0]=r[0]+lamda*np.sqrt(1-costheta**2)*np.cos(phi) #粒子组的x坐标r[1]=r[1]+lamda*np.sqrt(1-costheta**2)*np.sin(phi) #粒子组y坐标r[2]=r[2]+lamda*costheta #粒子组z坐标d = np.sum(np.reshape(r**2,((r**2).size)))drms.append(np.sqrt(d/m)) #走i次对应的均方根距离return drmsa = drms(50)
b = drms(500)
c = drms(5000)plt.plot(t,a,'o',markersize='3',marker='+',label='50-paths',color='r')
plt.plot(t,b,'o',markersize='3',marker='*',label='500-paths',color='g')
plt.plot(t,c,'o',markersize='3',marker='x',label='5000-paths',color='b')
plt.xlabel('Number of collisions')
plt.ylabel('<d>/lambda')
plt.plot(t,np.sqrt(t),label='Sqrt(N)',color = 'b')
plt.legend()
plt.show()
P-M-2.py
import numpy as np
import matplotlib.pyplot as pltN=1000 #总步数,即每次实验走N步t = [i for i in range(1,N+1)]def drms(m,a):drms=[]#计算均方根距离: for i in range(1,N+1,1): #3d-球坐标系,利用角参数\thata,\phi 描述其移动,走N步r=np.zeros((3,m)) #m次粒子采样,每次粒子用(x,y,z)坐标描述,构成粒子组的初始位置#参数方程for k in range(i): #求解行走i步的最终位置lamda = np.random.uniform(a,2-a,1)phi=np.random.uniform(0,2*np.pi,m) #生成m个随机数costheta=np.random.uniform(-1,1,m) #生成m个随机数r[0]=r[0]+lamda*np.sqrt(1-costheta**2)*np.cos(phi) #粒子组的x坐标r[1]=r[1]+lamda*np.sqrt(1-costheta**2)*np.sin(phi) #粒子组y坐标r[2]=r[2]+lamda*costheta #粒子组z坐标d = np.sum(np.reshape(r**2,((r**2).size)))drms.append(np.sqrt(d/m))return drmsa = drms(500,0.1)
b = drms(500,0.2)
c = drms(500,0.3)
d = drms(500,0.4)
e = drms(500,0.5)
f = drms(500,0.6)
g = drms(500,0.7)
h = drms(500,0.8)
i = drms(500,0.9)plt.plot(t,a,'o',markersize='3',marker='+',label='0.1-1.9',color='r')
plt.plot(t,b,'o',markersize='3',marker='*',label='0.2-1.8',color='g')
plt.plot(t,c,'o',markersize='3',marker='x',label='0.3-1.7',color='b')plt.plot(t,d,'o',markersize='3',marker='x',label='0.4-1.6',color='r')
plt.plot(t,e,'o',markersize='3',marker='+',label='0.5-1.5',color='g')
plt.plot(t,f,'o',markersize='3',marker='*',label='0.6-1.7',color='b')plt.plot(t,g,'o',markersize='3',marker='*',label='0.7-1.3',color='r')
plt.plot(t,h,'o',markersize='3',marker='x',label='0.8-1.2',color='g')
plt.plot(t,i,'o',markersize='3',marker='+',label='0.9-1.1',color='b')plt.xlabel('Number of collisions')
plt.ylabel('<d>/lambda')
plt.plot(t,np.sqrt(t),label='Sqrt(N)',color = 'b')
plt.legend()
plt.show()
Problem 3 随机游走的正态性校验
P3.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)s = time.time()
N = 100000
N = int(N)
Num = 10000
Num = int(Num)Choice = np.random.choice([-1,1],(N,Num))
Sum = sum(Choice[:,])e = time.time()
print("time:",round(e-s,2))
##plt.hist(Sum,50)
##plt.title("Distribution of position")
##plt.savefig("Distribution of position.jpg")
##plt.pause(0.01)Position = np.zeros(2061)
for i in range(-1030,1031):Position[i] = len(np.where(Sum>i)[0])/Num
##plt.plot(range(1031),Position)
##plt.savefig("P3-c.jpg")
##plt.pause(0.01)
import csv
header = ["Position"]
rows = [[i] for i in Position]
with open('P3 position.csv','w',newline="") as file:writer = csv.writer(file)writer.writerow(header)writer.writerows(rows)
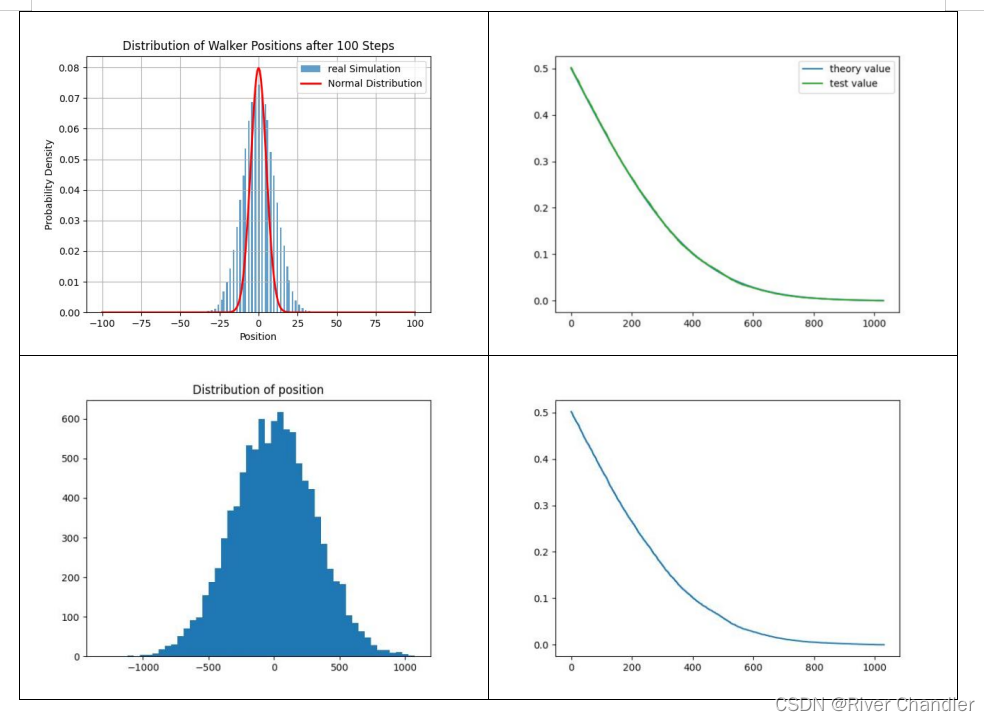
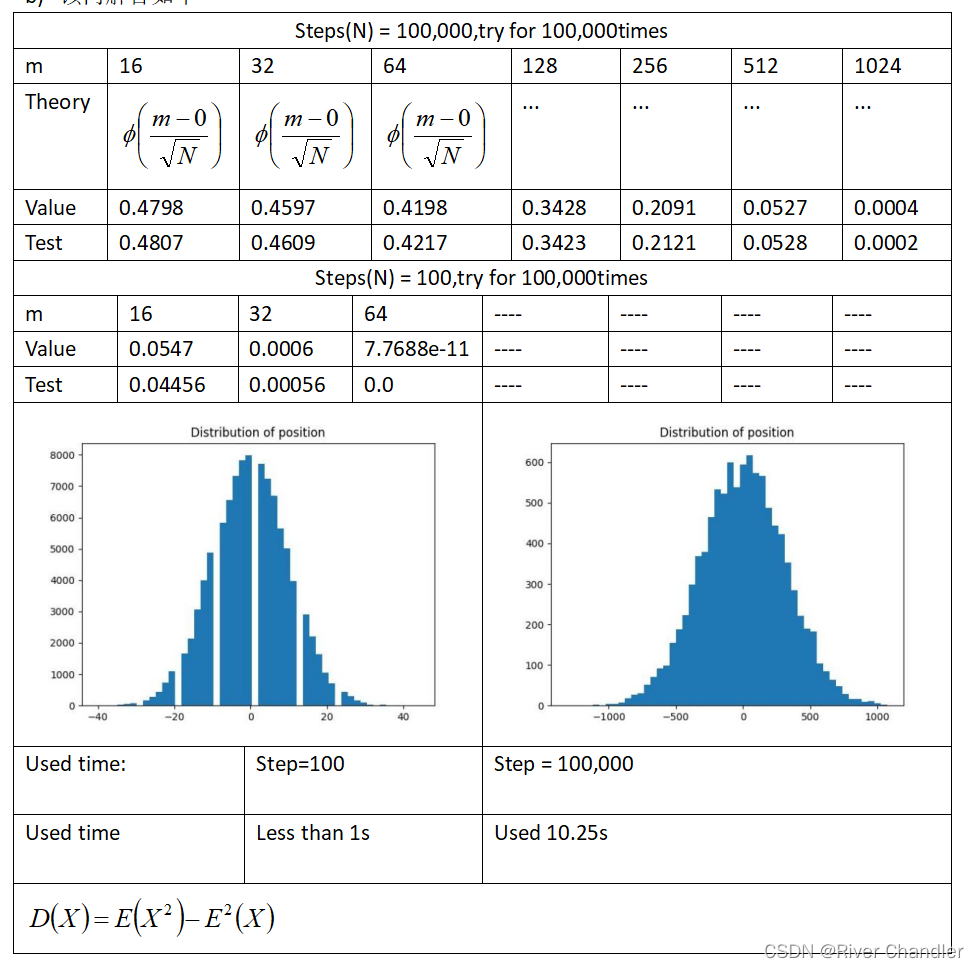
从前面的图中可以看出,对于足够大的N,计算出的分布可以用高斯分布来近似
| 样本量 | 中位数 | 平均值 | 标准差 | 偏度 | 峰度 | S-W检验 | K-S检验 |
| 2061 | 0.502 | 0.5 | 0.405 | -0.001 | -1.713 | 0.829(0.000***) | 0.149(1.1e-40) |
P3-e.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)s = time.time()
#step:N
N = 3000
N = int(N)
#repeat:Num
Num = 10000
Num = int(Num)Choice = np.random.random((N,Num))
CHOICE = np.zeros((N,Num))
for i in range(N):for j in range(Num):if Choice[i][j] <= 0.7:CHOICE[i][j] = 1else:CHOICE[i][j] = -1
Sum = sum(CHOICE[:,])e = time.time()
print("time:",round(e-s,2))
plt.hist(Sum,50)
plt.title("Distribution of position-e")
plt.savefig("Distribution of position-e N3000.jpg")
plt.pause(0.01)import csv
header = ["Position"]
rows = [[i] for i in Sum]
with open('P3-e position N3000.csv','w',newline="") as file:writer = csv.writer(file)writer.writerow(header)writer.writerows(rows)
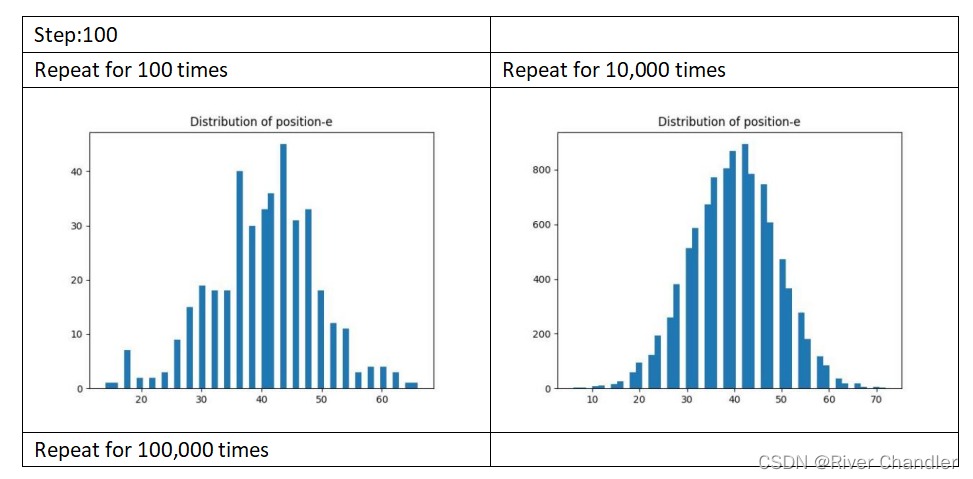
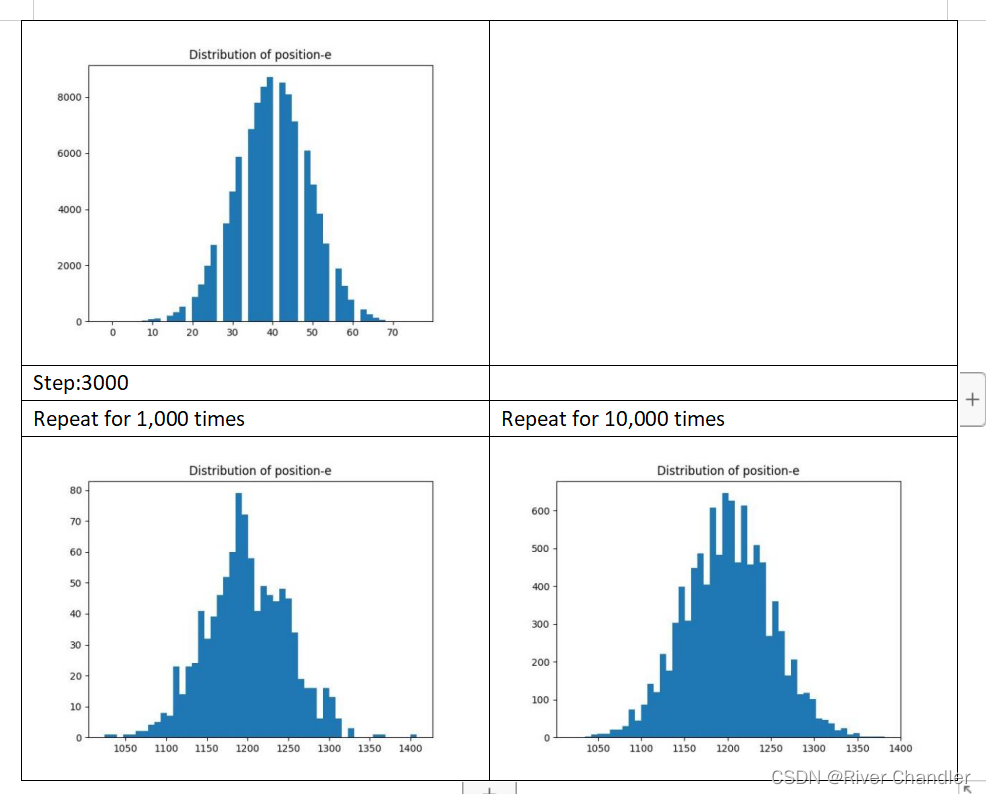
修改概率使得向正向移动概率为0.7

P3-f.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Num = 10000
T = [100,200,500,1000,1500,3000,10000,50000,100000]
R = []
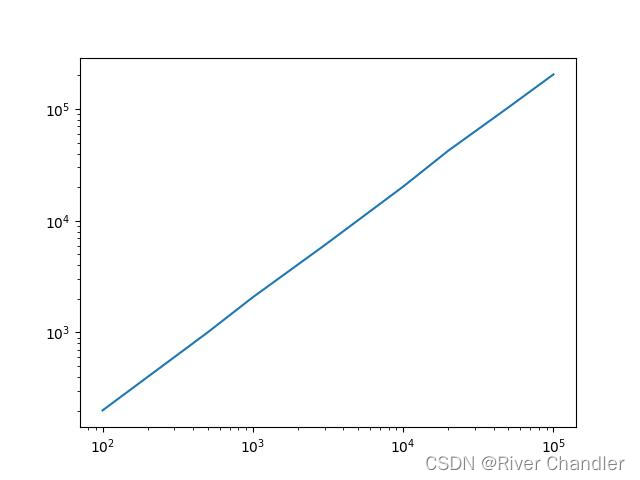
for N in T:s = time.time()Choice = np.random.choice([-1,1],(N,Num))Sum = sum(Choice[:,])R.append(sum(Sum**2)/Num)e = time.time()print("time:",round(e-s,2))plt.loglog(T,R)
plt.title("log-log E(x^2)-Num")
plt.savefig("P3-f-2.jpg")
plt.pause(0.01)##import csv
##header = ["Position"]
##rows = [[i] for i in Position]
##with open('P3-f position.csv','w',newline="") as file:
## writer = csv.writer(file)
## writer.writerow(header)
## writer.writerows(rows)
走N步,轴上移动的距离为X
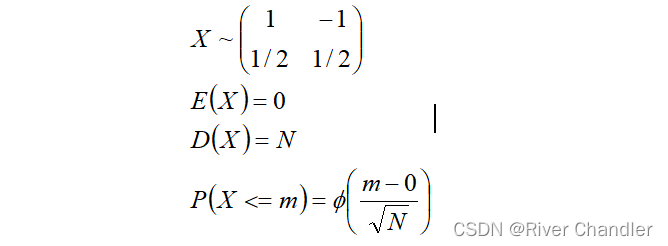
Problem 4 二维随机游走的自封闭性
Flory exponent.py
##Flory exponent 是描述聚合物空间构型的一种指标,
##其值越大表明聚合物链越趋于伸展状态,反之则趋于卷曲状态。
##
##在随机游走模型中,
##可以通过生成随机步长并多次重复步骤来模拟聚合物链的构型演化。
##通过计算链的端到端距离 $R$ 与聚合物链长度 $N$ 之间的关系,可以得到 Flory exponent $v$ 的估计值。
##
import numpy as npnum_walks = 100 # 模拟次数
max_steps = 100 # 聚合物链长度
step_size = 1 # 随机步长Rs = [] # 链的端到端距离列表# 多次重复模拟
for i in range(num_walks):positions = np.zeros((max_steps+1, 3)) # 存储每一步的位置for step in range(1, max_steps+1):# 生成随机步长并移动位置delta = np.random.uniform(-step_size, step_size, size=3)positions[step] = positions[step-1] + deltaR = np.linalg.norm(positions[-1] - positions[0]) # 计算链的端到端距离Rs.append(R)N = np.arange(1,max_steps+1)
v = np.polyfit(np.log(N), np.log(Rs), deg=1)[0] # 拟合直线斜率即为 Flory exponentprint(f"Flory exponent = {v:.3f}")
##这段代码使用了 NumPy 库来进行向量化计算,
##并通过多次模拟生成了随机游走聚合物链的构型。最后,使用最小二乘法拟合直线斜率来估计 Flory exponent 的值。
##
P4 forge.py
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(0)Times1 = np.array([0.8,1.1,1.5,1.8,2.0,2.1,2.4])
Times2 = np.linspace(2.5,6,30)D1 = 4/3*Times1
D2 = 4/3*Times2plt.plot(Times1,D1,lw=2)
plt.plot(Times2,D2,lw=2)noise1 = np.random.uniform(-0.1,0.1,7)
noise2 = np.random.uniform(-0.1,0.1,30)D1 += noise1
D2 += noise2plt.scatter(Times1,D1,s=3)
plt.scatter(Times2,D2,s=3)plt.xlabel("Time")
plt.ylabel("$D^2$")
plt.title("<D^2> versus T for self avoiding walk in 2D")
plt.pause(0.01)
P4-a.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Ne = [100,500,1000,3000,10000,20000,50000,100000]
Re = []Num = 1000for N in Ne:SUM = np.zeros(Num)s = time.time()for j in range(Num):Choicex = np.random.choice([-1,1],N)Choicey = np.random.choice([-1,1],N)SUM[j] = sum(Choicex)**2 + sum(Choicey)**2e = time.time()print(round(e-s,2),"s")Re.append(sum(SUM)/Num)##plt.hist(SUM,50)
##plt.title("Distribution of position 2D sample")
##plt.pause(0.01)
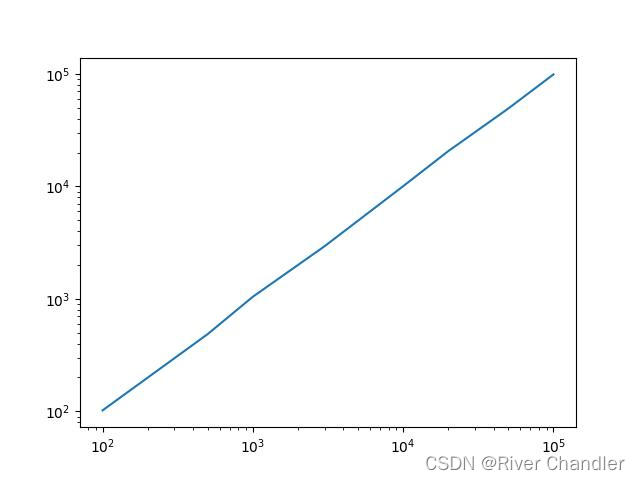
v = np.polyfit(2*np.log(np.array(Ne)),np.log(Re),deg=1)[0] # 拟合直线斜率即为 Flory exponent
print("v:",v)
P4-b.py
import matplotlib.pyplot as plt
import numpy as np
import timenp.random.seed(0)Num = 1000Ne = [100,500,1000,3000,10000,20000,50000,100000]
Re = []for N in Ne:SUM = np.zeros(Num)s = time.time()for j in range(Num): Choicex = np.random.choice([-1,1],N)Choicey = np.random.choice([-1,1],N)temp = np.random.random(N)temp1 = np.where(temp>=0.5)[0]temp2 = np.where(temp<0.5)[0]SUM[j] = sum(Choicex[temp1])**2 + sum(Choicey[temp2])**2e = time.time()print(round(e-s,2),"s")Re.append(sum(SUM)/Num)NUM = np.arange(1,Num+1)
v = np.polyfit(2*np.log(np.array(Ne)),np.log(Re),deg=1)[0] # 拟合直线斜率即为 Flory exponent
print("v:",v)##plt.hist(SUM,50)
##plt.title("Distribution of position 2D sample")
##plt.pause(0.01)
P4-图像绘制.py
import random
import turtle
count = 0#死点的计数
#判断是否走过
def Judge(xl,yl,listx,listy):res=Falsefor i in range(len(listx)):if xl==listx[i] and yl==listy[i]:#成对判断坐标是否已存在res=Truereturn res
#判断是否死点
def Die(x,y,listx,listy):x1=x+10x2=x-10y1=y-10y2=y+10Res=Judge(x1,y,listx,listy)&Judge(x2,y,listx,listy)&Judge(x,y1,listx,listy)&Judge(x,y2,listx,listy)return Res
#地图可视化
def Map(size):xs = -((size*10)//2)turtle.pensize(1)turtle.speed(10)#纵坐标的线绘制for y in range(-((size*10)//2),((size*10)//2)+1,10):turtle.penup()turtle.goto(xs,y)turtle.pendown()turtle.forward(size*10)#横坐标线绘制ys = ((size*10)//2)turtle.right(90)for x in range(-((size*10)//2),((size*10)//2)+1,10):turtle.penup()turtle.goto(x,ys)turtle.pendown()turtle.forward(size*10)
#路径绘制函数
def Draw(size):global countx = y = 0listx=[0]listy=[0]#设定笔的属性turtle.pensize(2)turtle.speed(0)turtle.color("red")#模拟走动(是个方向等概率)turtle.penup()turtle.goto(0,0)turtle.pendown()while abs(x) < ((size*10)//2) and abs(y) < ((size*10)//2):r = random.randint(0,3)#产生随机数,0右,1下,2左,3上表示是个方向if Die(x,y,listx,listy):#判断死点count+=1#计数breakelif r == 0:#右x += 10 if Judge(x,y,listx,listy):#判断是否为走过的点x-=10 #是的话坐标不变continue#终止本次循环else:listx.append(x)listy.append(y)turtle.setheading(0)turtle.forward(10)elif r == 1:#下y -= 10if Judge(x,y,listx,listy):y+=10continueelse:listx.append(x)listy.append(y)turtle.setheading(270)turtle.forward(10)elif r == 2:#左x -= 10if Judge(x,y,listx,listy):x+=10continueelse:listx.append(x)listy.append(y)turtle.setheading(180)turtle.forward(10)elif r == 3:#上y += 10if Judge(x,y,listx,listy):y-=10continueelse:listx.append(x)listy.append(y)turtle.setheading(90)turtle.forward(10)
#主程序部分
if __name__ == "__main__":temp = 'a'if temp=='a':turtle.hideturtle()#隐藏画笔Map(16)Draw(16)turtle.done()elif temp=='b':turtle.tracer(False)#隐藏动画效果for i in range(10,51): #模拟地图规模变化count=0#每次变化对死点计数器初始化for j in range(0,10000):#10000次仿真训练Draw(i)turtle.reset()print('For lattice of size ',i,', the probability of dead-end paths is ',count/100,'%')else:print('input error')
2D Sample Random Walk
-
拟合直线斜率
v: 0.5022164965587219
选取点
100,500,1000,3000,10000,20000,50000,100000
2D Traditional Random Walk
选取点 100,500,1000,3000,10000,20000,50000,100000
拟合直线斜率 v: 0.49883658055370034
2D Self-Avoiding Random Walk
选取点 Range(2,20)
拟合直线1斜率 v: 1.3074916500876987
拟合直线2斜率 v: 1.502393127(3/4*2)
For each of the method,give the N big enough:
| 2D Sample Random Walk | 2D Traditional Random Walk | 2D Self Avoiding Random Walk |
| 3,000 is enough (Error:1e-2) | 3,000 is enough (Error:1e-2) | 50 is enough (Error:1e-2) |
| 其实考虑到自封闭, 完全可以将self-avoiding random walk 控制在1e2-1e3上,不选1e1下只是不够精确而言。 (即:我们如果向下图一样设置,使得random walk面临墙壁的控制,那么,50就足够了,但是从数学的角度上看,这很难得到完整的证明,因为绝大多数的小数位是内置函数和内置定量的精度所控制的) | ||
相关文章:

计算物理专题----随机游走实战
计算物理专题----随机游走实战 Problem 1 Implement the 3D random walk 拟合线 自旋的 拟合函数(没有数学意义) 参数:0.627,3.336,0.603,-3.234 自由程满足在一定范围内的均匀分布以标准自由程为单位长度,…...
《思维与智慧》简介及投稿邮箱
《思维与智慧》自1982年创刊,经国家新闻出版署批准,由河北省教育厅主管,河北行知文化传媒有限责任公司主办的益智励 志类大众文化期刊。 《思维与智慧》办刊宗旨是:“开发思维,启迪智慧,滋润心灵”&#x…...

flask+python快速搭建
app.py """APP 入口模块""" from traceback import format_excfrom api_limiter import limiter from flask import Flask, jsonify import loggingfrom controller import api_sql_blueapp Flask(__name__) limiter.init_app(app) app.regist…...
基于微信小程序的美术馆预约平台设计与实现(源码+lw+部署文档+讲解等)
前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...
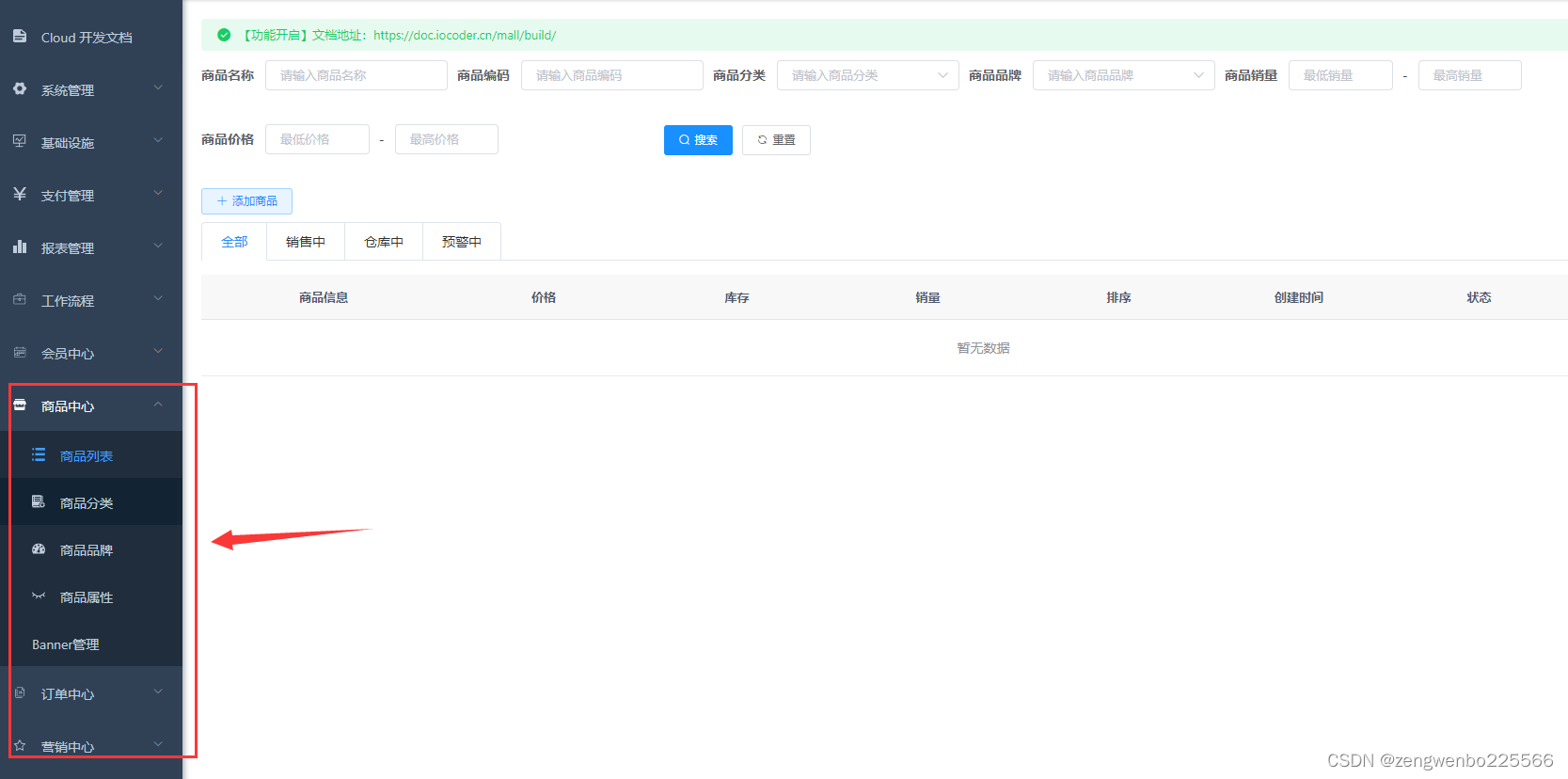
ruoyi-vue-pro yudao 项目商城 mall 模块启用及相关SQL脚本
目前ruoyi-vue-pro 项目虽然开源,但是商城 mall 模块被屏蔽了,查看文档却要收费 199元(知识星球),价格有点太高了吧。 分享下如何启用 mall 模块,顺便贴上sql相关脚本。 一、启用模块 修改根目录 pom.xm…...

default 和 delete 与默认构造函数 的使用
前言 使用default和delete关键字来干预编译器自动生成的函数。让我详细解释一下这些知识点: 正文 编译器生成的默认构造函数: 如果类A没有定义任何构造函数,那么编译器会自动生成一个无参的默认构造函数 A()。这个默认构造函数实际上是一个…...
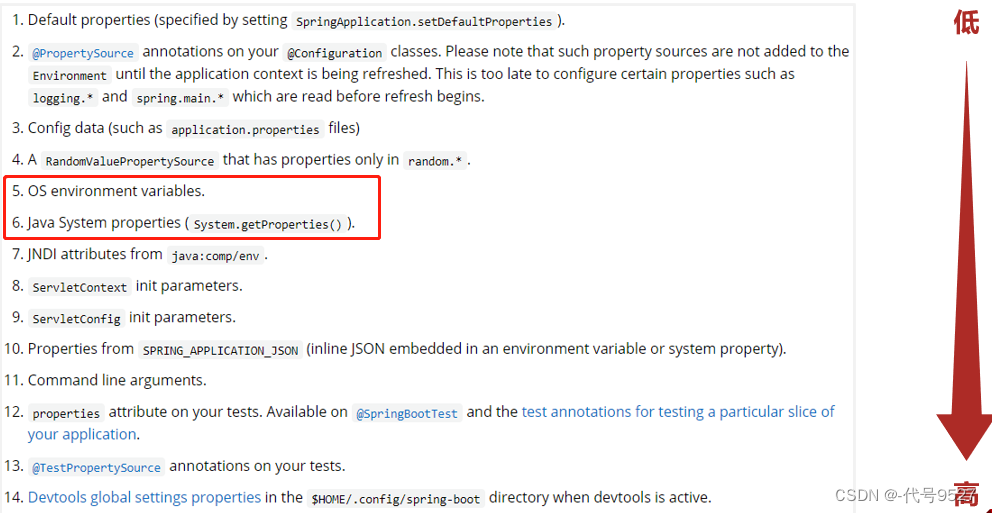
【开发篇】一、热部署
文章目录 1、手工启动热部署2、自动启动热部署3、热部署范围配置4、关闭热部署功能 1、手工启动热部署 日常开发与调试,改几行代码想看效果就得手动点重启,很繁琐,接下来考虑启动热部署。首先引入springboot开发者工具: <dep…...
)
点云从入门到精通技术详解100篇-定子装配过程中基于深度学习的易变形材料的点云分割(下)
目录 4.3.2 校正网络 4.3.3 浅层特征提取网络 4.3.4 空间边界 Transformer 深层特征提取网络 4.3.5 损失函数...
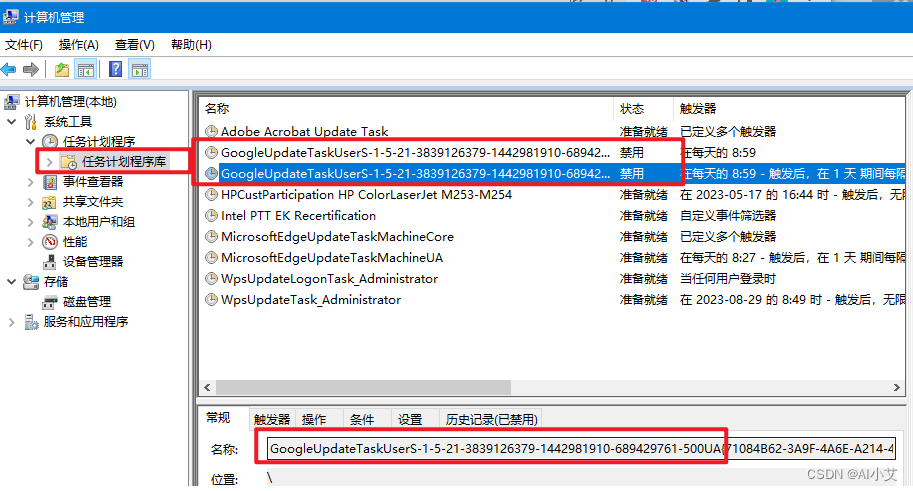
谷歌浏览器关闭自动更新功能
背景:自动化测试需要下载webdriver驱动,然而浏览器自动更新会导致原来的驱动版本与现有浏览器版本不匹配,所以要禁用掉浏览器自动更新功能。 1.右键-我的电脑-打开管理; 2.选择任务计划程序-任务计划程序库-找到两个chrome自动更新…...

电商业务--技术负责人 250K*15
职位描述 研发团队管理 系统搭建 技术管理 系统架构 岗位职责 负责/参与到中大型负责系统的整体架构和设计; 根据业务特点和行业最佳实践,设计符合多个市场物流业务需求,且具备可扩展能力的系统架构和业务架构承担团队稳定性建设工作&#…...

MySQL只同步单个表或多个表,非全部同步!
replicate-do-table 是 MySQL 复制配置中的一个选项,它允许您指定要在从服务器上复制的表。如果您想要只复制主服务器上特定的表到从服务器,您可以使用这个选项。 以下是如何操作 replicate-do-table 的步骤: 停止从服务器: 在从服务器上执行…...

【论文基本功】【LaTeX】个人常用易忘LaTeX命令
【论文基本功】【LaTeX】个人常用易忘LaTeX命令 1. 基本符号2. 引用3. 字体及符号大小4. 其他参考 1. 基本符号 符号LaTeX命令备注 ∣ ⋅ ∣ | \cdot | ∣⋅∣| \cdot |绝对值 ∣ ∣ ⋅ ∣ ∣ || \cdot || ∣∣⋅∣∣\| \cdot \|范数 ⌈ ⋅ ⌉ \lceil \cdot \rceil ⌈⋅⌉\lce…...

JVM参数调优——G1收集器
开启 G1 Collector G1收集器的出现除了提供可控的低延迟GC,解决历史收集器的一些弊病,同时还尽力简化调优参数 对于大多数应用,开启收集器,再配置一下Xms和Xmx就足够了(不建议配置Xmn) -XX:UseG1GC核心参…...

Linux cp命令使用指南:详细教程及实际应用场景解析
文章目录 Linux中的cp命令使用指南1. 简介1.1 Linux操作系统简介1.2 文件系统和目录结构1.3 cp命令概述 2. cp命令基本用法2.1 复制文件2.2 复制目录2.3 复制多个文件或目录2.4 递归复制2.5 强制覆盖已存在文件2.6 保留文件权限和属性 3. 高级用法3.1 保留符号链接3.2 仅复制更…...
树结构数据在table中回显 treeselect disabled
<el-table-column label"产业认定" align"center" prop"industryIdentification"><template slot-scope"scope"><treeselectv-if"scope.row.industryIdentification"v-model"scope.row.industryIdentif…...

BOA服务器移植
BOA服务器移植 1、源码下载 http://www.boa.org/ News! (last updated 23 February 2005) Latest Released Version (0.94.13) here (signature here) --- 下载地址1.1 boa简介: 其可执行代码只有大约60KB左右,Boa是一个单任务的HTTP服务器ÿ…...

洛谷刷题入门篇:顺序结构
链接如下:https://www.luogu.com.cn/training/100#problems 一、Hello,World! 题目链接:https://www.luogu.com.cn/problem/B2002 题目描述 编写一个能够输出 Hello,World! 的程序。 提示: 使用英文标点符号;Hello,World! 逗…...

LVS+Haproxy
LVSHaproxy 一、Haproxy简介1.1、Haproxy应用分析1.2、Haproxy的特性1.3、常见负载均衡策略1.4、LVS、Haproxy、Nginx区别1.5、 Haproxy的优点1.6、常见的Web集群调度器 二、Haproxy部署实例四、日志定义优化 一、Haproxy简介 Haproxy 是一个使用C语言编写的自由及开放源代码软…...

Linux知识
文章目录 一、Apt1、查看操作系统信息2、换源3、比较4、用法5、ubuntu获取源码 二、pkg-config三、调试glibc 一、Apt 1、查看操作系统信息 使用以下命令查看本机的操作系统和位数信息: uname -m && cat /etc/*release输出: x86_64 DISTRIB_I…...
Java基础(三)
前言:前面主要涉及到java的基本语法,接下来本篇博客主要记录Java中Collections类、泛型、以及File类、IO流的学习。 目录 数据结构 泛型 集合 分类 Collection的分类 collection常用方法 collection遍历方式 迭代器 for循环 Lambda表达式 Lis…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...