【力扣每日一题】2023.9.21 收集树中金币
目录
题目:
示例:
分析:
代码:
题目:
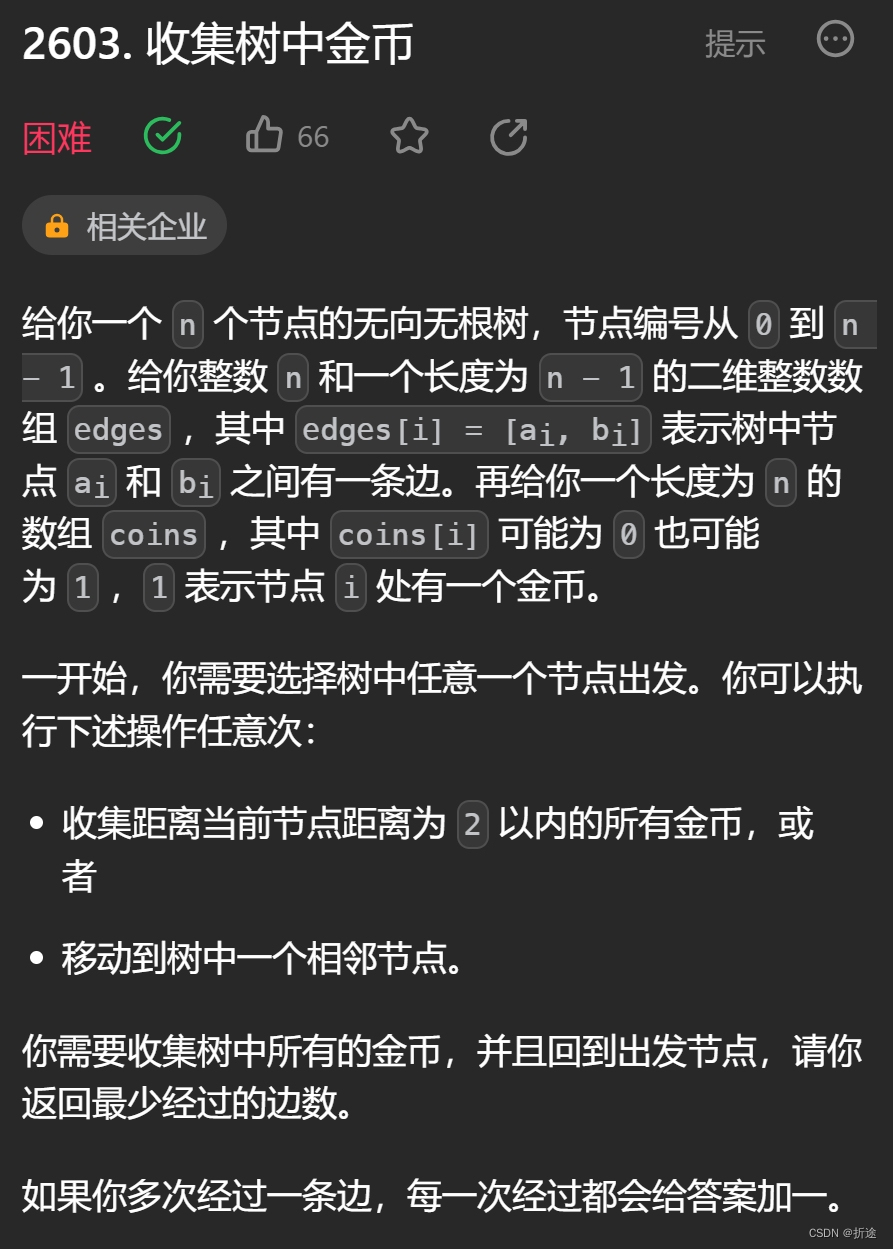
示例:
分析:
题目给我们一棵树,不过这棵树不是普通的树,而是无向无根树。给我们一个二维数组表示节点之间的连接关系,以及一个一维数组表示每个节点是否有金币。
我们可以从任何一个节点出发,并且可以收集距离两格的节点的金币,每次可以移动到相邻的节点。问我们要收集完所有的金币并且最终要回到起点,最少需要移动几次。
首先,题目说了这是一棵树,所以是不存在环的,两个节点之间连通的路径只会有唯一的一条。
因此我们不管选择哪一个节点当起点,都是可以到达任意一个节点的。
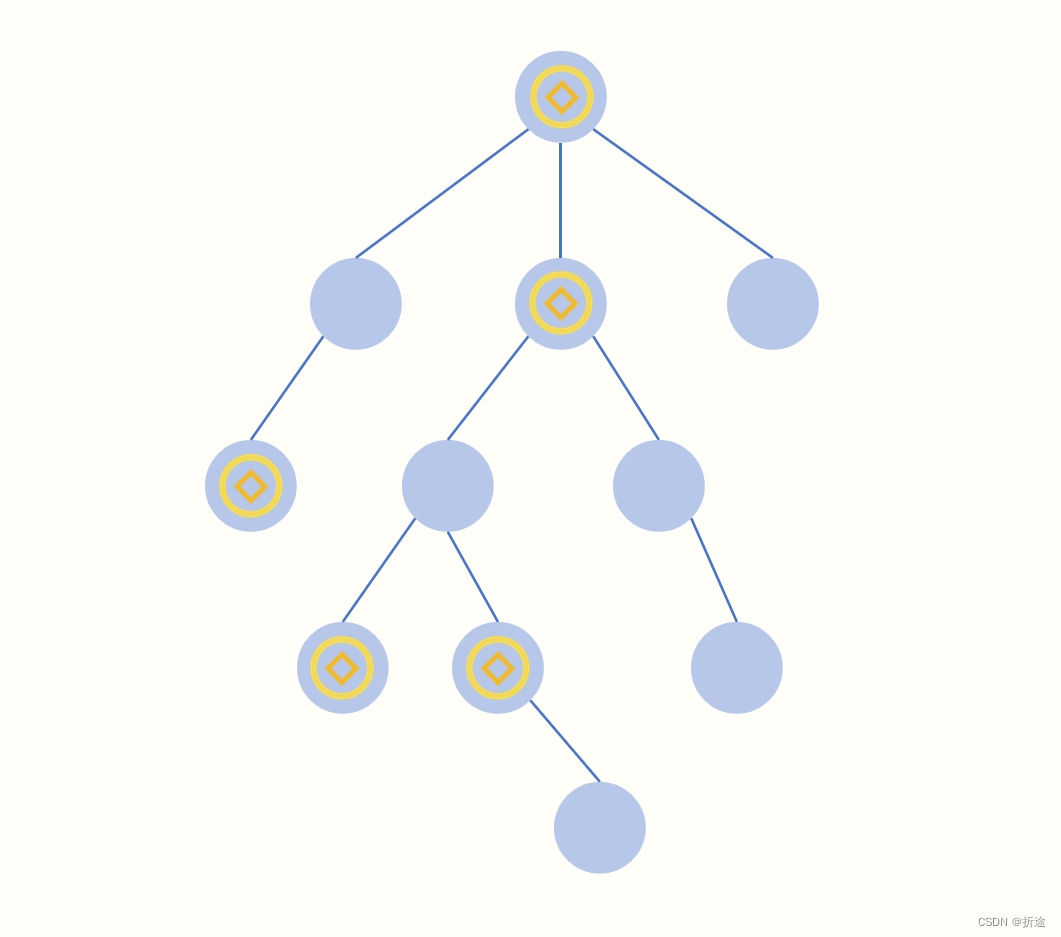
我们需要获取所有的金币,那么如果一个节点没有金币,并且这个节点是叶子节点,那么我们是不是可以将这个节点直接从树中移除,因为我们根本不需要走到这个节点。
我们把能删除的节点都删除了,是不是就说明剩下的节点都是我们需要走到或是收集金币的节点。
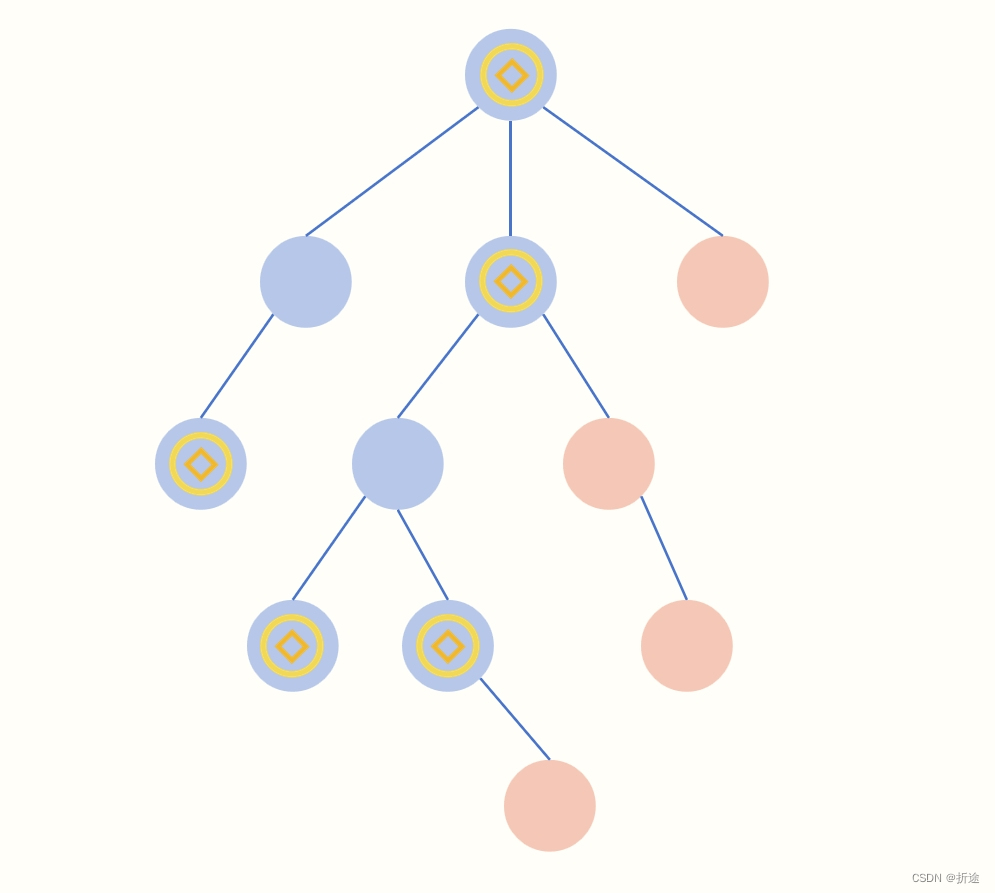
如果我们把整棵树剪到只剩下我们必须要走到的节点之后,答案就剩下节点数-1再乘2了。
为什么呢?
题目要求我们必须在收集完金币之后再返回原点,我们有n个必须到达的节点,由于这是树,是没有环的,因此节点之间的连线一共是n-1条。一来一回每个线段要走两次,所以答案是(n-1)*2
问题就变成了我们怎么把树的节点剪到只剩下我们必须要走的节点。
首先,没有金币的叶子节点我们是可以先删除的。判断依据也简单,如果一个节点没有金币,并且和这个节点连接的其他节点只有一个,那么它就是没有金币的叶子节点,可以把它删除。并且删除某个节点之后可能会诞生出新的无金币叶子节点,因此我们删除节点之后还需要判断一下与这个节点连接的节点是否也是无金币叶子节点,也就是延伸性地删除节点。
那么怎么删除呢,我们可没有构建出树来。
我们其实不需要真的删除。我们之前分析过了,答案就是剪枝后的节点数减1再乘2。我们可以当成一开始的树就是我们剪枝后的树,把答案初始化成总的节点数减1再乘2。每次我们删除一个节点就等于是移除了一个线段,把答案减2即可,这样就当成是删除一个节点了。
初步移除了没有金币的叶子节点之后剩下的节点就是我们要达到的节点或者是要收集金币的节点了。
我们把剩下的树看成是图,那么图边缘一圈的节点一定都是有金币的。

我们收集金币的时候可以距离金币节点两格,因此我们可以再一次把图的外围两层节点删除,不过删除是有条件的,最外层的叶子节点可以直接删除,不过第二层的节点我们得判断删除了外层节点后,第二层的节点是不是叶子节点,如果是我们才可以删除。
最终我们每次删除节点之后,都将答案-2,最终就是要返回出去的答案了。
不过最后还有一个问题,那就是如果整个树都是可以移除的,那么根据我们刚才说的每删除一个节点就把答案-2,而我们答案初始化是总的节点数减1再乘2,这样答案就变成了-2,因此最后我们做个判断,如果答案小于0,我们就返回0,反之就正常返回求出的答案。
代码:
class Solution {
public:unordered_map<int,vector<int>>pic; //记录节点连接图unordered_map<int,int>rel; //记录每个节点的邻接数量关系int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {int n=coins.size();int res=2*(n-1); //答案初始化成图中线段数乘2,表示每个线段都要走两边//建图for(auto& edge:edges){if(pic.find(edge[0])==pic.end()) pic[edge[0]]=vector<int>(0);if(pic.find(edge[1])==pic.end()) pic[edge[1]]=vector<int>(0);pic[edge[0]].push_back(edge[1]);pic[edge[1]].push_back(edge[0]);rel[edge[0]]++;rel[edge[1]]++;}queue<int> q;//删除无金币的叶子节点(可延伸)for(int i=0;i<n;i++){if(coins[i]==0 && rel[i]==1) q.push(i);}while(!q.empty()){res-=2; //减少一个线段,答案减2,因为默认每个线段走两次.int cur=q.front();q.pop();for(int i:pic[cur]){if(--rel[i]==1&&coins[i]==0) q.push(i);}}//确定到有金币的叶子节点的范围.for(int i=0;i<n;i++){if(coins[i]==1&&rel[i]==1) q.push(i);}res-=2*q.size();//减少叶子节点,不延伸(因为可以收集距离两格的金币,所以可以在边缘处再缩小一圈)while(!q.empty()){int x=q.front();q.pop();for(int j:pic[x]){if(--rel[j]==1) res-=2;}}if(res>0) return res;return 0;}
};相关文章:

【力扣每日一题】2023.9.21 收集树中金币
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一棵树,不过这棵树不是普通的树,而是无向无根树。给我们一个二维数组表示节点之间的连接关系ÿ…...
Python与数据分析--每天绘制Matplotlib库实例图片3张-第1天
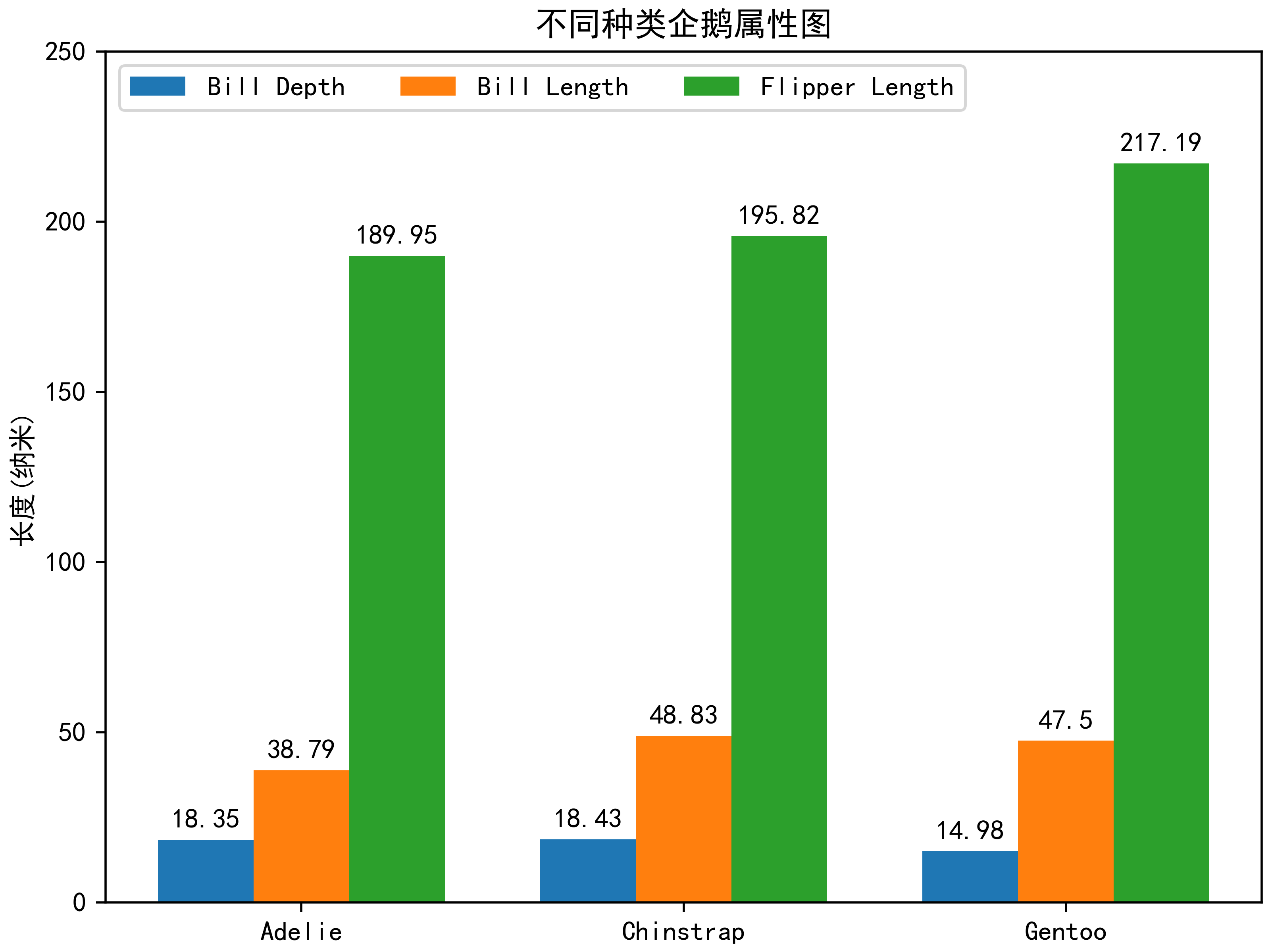
目录 1.实例1--Bar color demo 2.实例2--Bar Label Demo 3.实例3--Grouped bar chart with labels 1.实例1--Bar color demo import matplotlib.pyplot as plt # 支持中文 plt.rcParams[font.sans-serif] [SimHei] # 用来正常显示中文标签 plt.rcParams[axes.unicode_minus…...
pycharm 中package, directory, sources root, resources root的区别
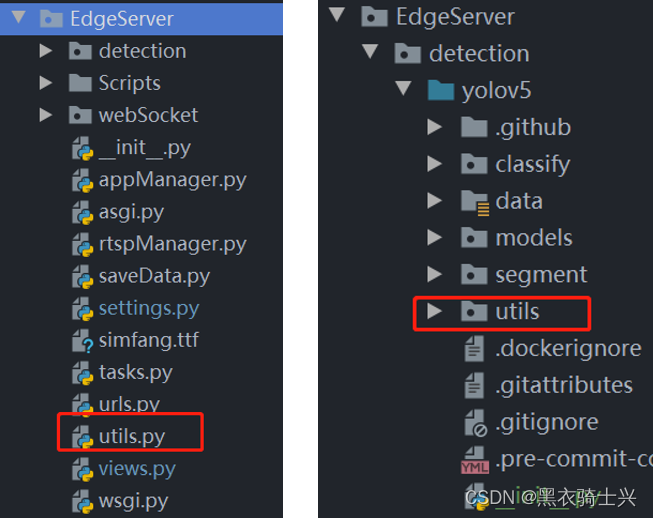
【遇到的问题】 导入yolov5中有utils文件,自己的代码中也有utils文件,使得yolov5中的这部分引用出错了。 【解决方案】 单独建立detection文件夹,把检测相关的都放在这里,yolov5是github上拉取的源码,发现yolov5中fr…...
【谢希尔 计算机网络】第2章 物理层
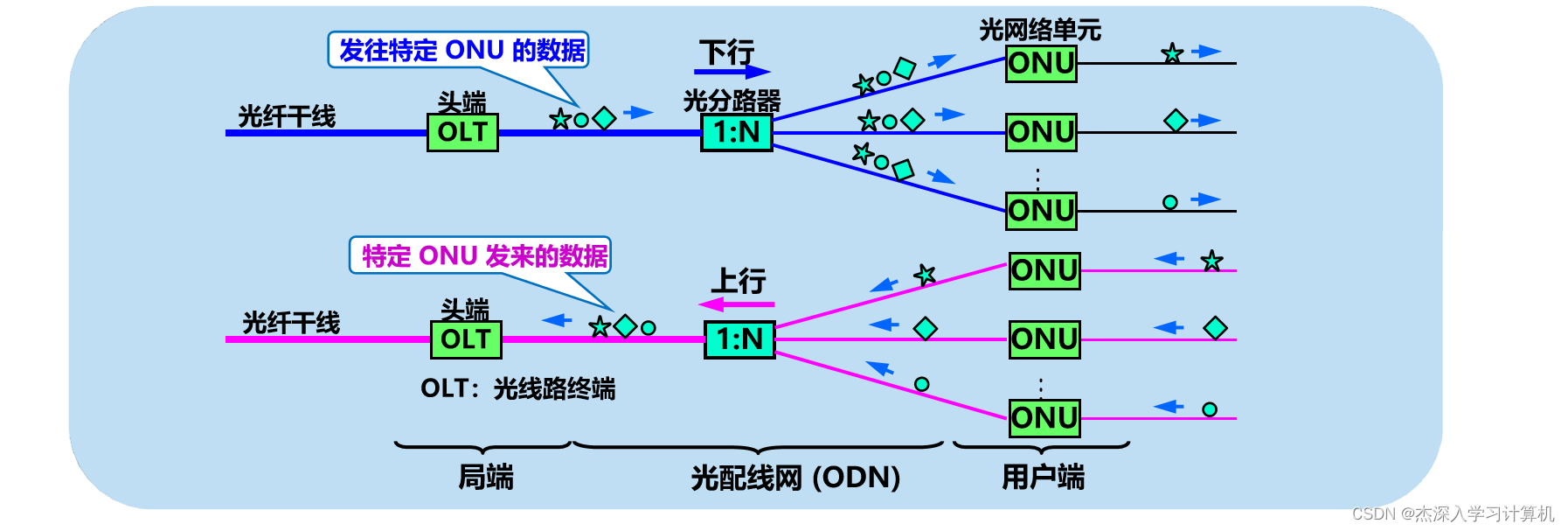
目录 通信基础 基本概念 两个公式lim 奈氏准则 香农定理 奈氏准则 VS 香农定理 编码与调制 编辑 物理层下面的传输媒体 导引型传输媒体 1. 双绞线 2. 同轴电缆 3. 光缆 非导引型传输媒体 无线电微波通信 卫星通信 无线局域网使用的 ISM 频段 信道复用技术 …...

Eclipse工具使用技巧
1、常用快捷键 ctrlshifto 快速导包 CtrlSpace 内容助理 说明:内容助理。提供对方法,变量,参数,javadoc等得提示,应运在多种场合,总之需要提示的时候可先按此快捷键。注:避免输入法的切换设置与此设置冲突 CtrlShiftSpace 变量提示 Ctrl/ 添加/消除//注释 CtrlShift/ 添加…...

python LeetCode 刷题记录 94
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 代码 递归 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.righ…...

滴滴可观测平台 Metrics 指标实时计算如何实现了又准又省?
在滴滴,可观测平台的 Metrics 数据有一些实时计算的需求,承载这些实时计算需求的是一套又一套的 Flink 任务。之所以会有多套 Flink 任务,是因为每个服务按照其业务观测需要不同的指标计算,也就对应了不同数据处理拓扑。我们尽力抽…...
每天几道Java面试题:IO流(第五天)
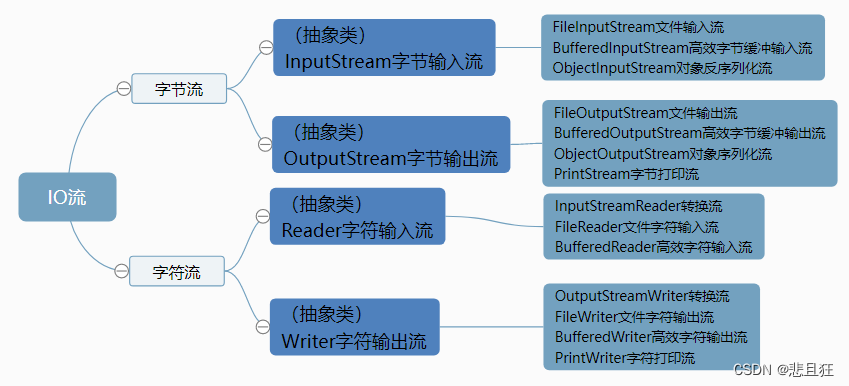
目录 第五幕 、第一场)街边 友情提醒 背面试题很枯燥,加入一些戏剧场景故事人物来加深记忆。PS:点击文章目录可直接跳转到文章指定位置。 第五幕 、 第一场)街边 【衣衫褴褛老者,保洁阿姨,面试者老王】 衣衫褴褛老…...

js/axios/umi-request 根据后端返回的二进制流下载文件
type ResponseType {data: Blob;headers: {content-disposition?: string;}; }; // 下载 (创建a标签) export const downloadBlob (response: ResponseType) > {const blob response.data; // 获取响应中的 Blob 数据const contentDisposition response.headers[conten…...

软件评测师之流水线
目录 一.概念二.周期三.执行时间的计算 一.概念 程序在执行时多条指令可以层叠并行的技术。 二.周期 取指→分析→执行 指令执行的各个阶段里面,执行时间最长的为流水线的周期。 三.执行时间的计算 n条指令执行的总时间流水线计算公式:单条指令所需…...
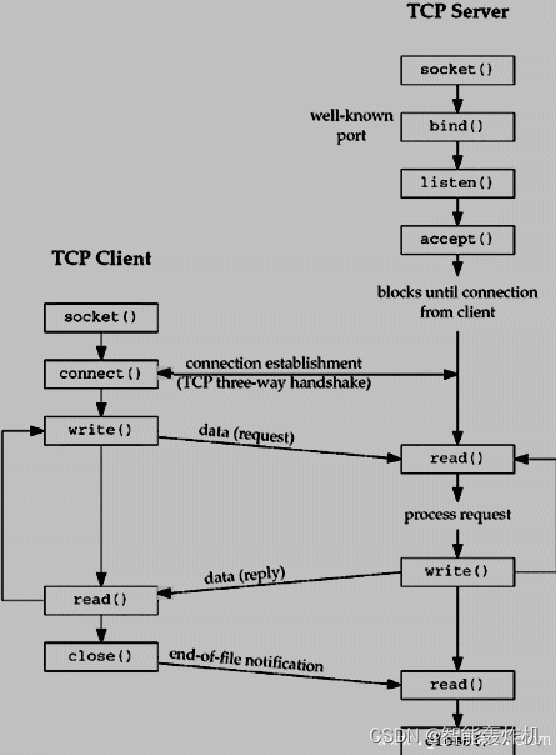
Linux系统编程——网络编程的学习
Linux系统编程学习相关博文 Linux系统编程——文件编程的学习Linux系统编程——进程的学习Linux系统编程——进程间通信的学习Linux系统编程——线程的学习 Linux系统编程——网络编程的学习 一、概述1. TCP/UDP2. 端口号3. 字节序4. Sockt服务器和客户端的开发步骤1. 服务器2…...

Vue中的ref 和$refs的使用
ref 和$refs 作用:利用ref 和$refs可以用于获取dom元素,或组件实例 特点:查找范围→当前组件内(更精确稳定,原生的dom在vue子组件中查找最终也会扫描到父组件) 1. 获取dom 目标标签–添加ref 属性 <…...

Hive【非交互式使用、三种参数配置方式】
前言 今天开始学习 Hive,因为毕竟但凡做个项目基本就避不开用 Hive ,争取这学期结束前做个小点的项目。 第一篇博客内容还是比较少的,环境的搭建配置太琐碎没有写。 Hive 常用使用技巧 交互式使用 就是我们正常的进入 hive 命令行下的使用…...
)
基于Yolov8的工业小目标缺陷检测(1)
目录 1.工业油污数据集介绍 1.1 小目标定义 1.2 难点 1.3 工业缺陷检测算法介绍 1.3.1 YOLOv8...

Python文件操作和管理指南:打开、读取、写入和管理文件
文章目录 文件(File)打开文件使用 with ... as 语句打开文件读取文件内容读取大文件的方式逐行读取和读取全部行写文件操作文件定位seek()tell() 关闭文件 文件管理获取目录结构获取当前目录切换当前所在目录创建目录删除目录删除文件重命名文件 总结pyt…...

WebGL 用鼠标控制物体旋转
目录 鼠标控制物体旋转 如何实现物体旋转 示例程序(RotateObject.js) 代码详解 示例效果 鼠标控制物体旋转 有时候,WebGL程序需要让用户通过鼠标操作三维物体。这一节来分析示例程序RotateObject,该程序允许用户通过拖动&…...

Spring Boot魔法:简化Java应用的开发与部署
文章目录 什么是Spring Boot?1. 自动配置(Auto-Configuration)2. 独立运行(Standalone)3. 生产就绪(Production Ready)4. 大量的起步依赖(Starter Dependencies) Spring …...

参议院算法Java
Dota2 的世界里有两个阵营: Radiant(天辉)和 Dire(夜魇) Dota2 参议院由来自两派的参议员组成。现在参议院希望对一个 Dota2 游戏里的改变作出决定,他们以一个基于轮为过程的投票进行。在每一轮中,每一位参议员都可以行使两项权利中的一项: 禁止一名参议员的权利:参…...
前端提交规范 ESLint + Prettier + husky + lint-staged
如何统一代码风格,规范提交呢? 推荐使用前端规范全家桶 ESLint Prettier husky lint-staged。 eslint (github.com/eslint/esli…)JavaScript 代码检测工具,检测并提示错误或警告信息prettier (github.com/prettier/pr…) 代码自动化格式…...
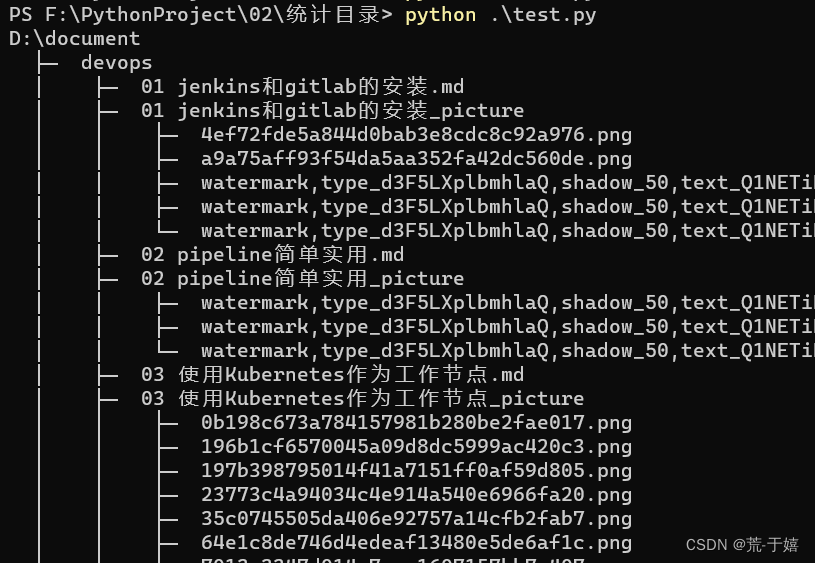
python实现命令tree的效果
把所有的文档都传到了git上,但是内容过多找起来不方便,突发奇想如果能在readme中,递归列出所有文件同时添加上对应的地址,这样只需要搜索到对应的文件点击就能跳转过去了… 列出文件总得有个显示格式,所以就按照tree的来了… 用python实现命令tree的效果 首先,这是tree的效果…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
