代码随想录算法训练营Day56 | 动态规划(16/17) LeetCode 583. 两个字符串的删除操作 72. 编辑距离
动态规划马上来到尾声了,当时还觉得动态规划内容很多,但是也这么过来了。
第一题
583. Delete Operation for Two Strings
Given two strings
word1andword2, return the minimum number of steps required to makeword1andword2the same.In one step, you can delete exactly one character in either string.
本题和LC 115 相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的
class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)return dp[-1][-1]第二题
72. Edit Distance
Given two strings
word1andword2, return the minimum number of operations required to convertword1toword2.You have the following three operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
编辑距离是用动规来解决的经典题目,这道题目看上去好像很复杂,但用动规可以很巧妙的算出最少编辑距离。利用动态规划五部曲来做一个分析:
1. 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
2. 确定递推公式
整体来讲,有如下几种操作:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换if (word1[i - 1] == word2[j - 1])那么说明不用任何编辑,dp[i][j]就应该是dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];-
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。即
dp[i][j] = dp[i - 1][j] + 1; - 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。即
dp[i][j] = dp[i][j - 1] + 1; - 操作三:替换元素,
word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。即
3. dp数组如何初始化
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
4. 确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的。
5. 举例推导dp数组
class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1return dp[-1][-1]相关文章:
 LeetCode 583. 两个字符串的删除操作 72. 编辑距离)
代码随想录算法训练营Day56 | 动态规划(16/17) LeetCode 583. 两个字符串的删除操作 72. 编辑距离
动态规划马上来到尾声了,当时还觉得动态规划内容很多,但是也这么过来了。 第一题 583. Delete Operation for Two Strings Given two strings word1 and word2, return the minimum number of steps required to make word1 and word2 the same. In on…...
HTML+CSS+JavaScript 大学生网页设计制作作业实例代码 200套静态响应式前端网页模板(全网最全,建议收藏)
目录 1.介绍2.这样的响应式页面这里有200套不同风格的 1.介绍 资源链接 📚web前端期末大作业 (200套) 集合 Web前端期末大作业通常是一个综合性的项目,旨在检验学生在HTML、CSS和JavaScript等前端技术方面的能力和理解。以下是一些可能的Web前端期末大…...

CFimagehost私人图床本地部署结合cpolar内网穿透实现公网访问
文章目录 1.前言2. CFImagehost网站搭建2.1 CFImagehost下载和安装2.2 CFImagehost网页测试2.3 cpolar的安装和注册 3.本地网页发布3.1 Cpolar临时数据隧道3.2 Cpolar稳定隧道(云端设置)3.3.Cpolar稳定隧道(本地设置) 4.公网访问测…...

uniapp瀑布流布局写法
首先我们要清楚瀑布流是什么? 瀑布流布局(Waterfall Flow Layout),也称为瀑布流式布局,是一种常见的网页或移动应用布局方式,特点是元素以不规则的方式排列,就像瀑布中的流水一样,每…...
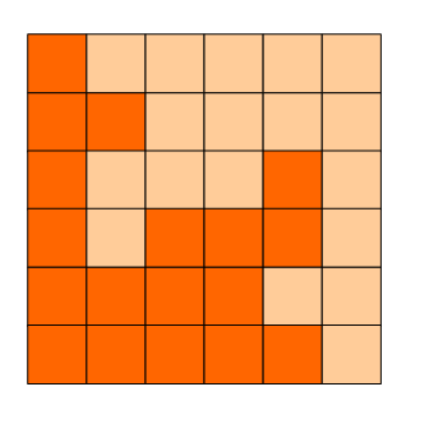
蓝桥杯 题库 简单 每日十题 day8
01 扫雷 题目描述 在一个n行列的方格图上有一些位置有地雷,另外一些位置为空。 请为每个空位置标一个整数,表示周围八个相邻的方格中有多少个地雷。 输入描述 输入的第一行包含两个整数n,m。 第2行到第n1行每行包含m个整数,相邻整…...

Keepalived 高可用(附带配置实例,联动Nginx和LVS)
Keepalived 一、Keepalived相关知识点概述1.1 单服务的风险(单点故障问题)1.2 一个合格的集群应该具备的特性1.3 VRRP虚拟路由冗余协议1.4 健康检查1.5 ”脑裂“现象 二、Keepalived2.1 Keepalived是什么?2.2 Keepalived体系主要模块及其作用…...

第二证券:今年来港股回购金额超700亿港元 9月近200家公司获增持
本年以来,港股上市公司回购力度不断增强。据恒生指数公司计算,到9月15日,本年以来港股回购金额到达735亿港元,占去年全年总额的70%。该公司预测,2023年港股回购金额可能到达929亿港元,是前5年年度平均水平的…...

Autosar基础——RTE简介
AutoSAR文章目录 AUTomotive Open System Architecture Autosar-简介和历史发展 Autosar-软件架构 Autosar软件组件-Application Layer介绍和SWC(Software Component)类型 Autosar-Runnables(可运行实体) Autosar-OS配置 Autosar IOC机制(核间通信) Autosar实践-CANTp Auto…...

几个国内可用的强大的GPT工具
前言: 人工智能发布至今,过去了九个多月,已经成为了我们不管是工作还是生活中一个重要的辅助工具,大大提升了效率,作为一个人工智能的自然语言处理工具,它给各大行业的提供了一个巨大的生产工具,…...

《Python等级考试(1~6级)历届真题解析》专栏总目录
❤️ 专栏名称:《Python等级考试(1~6级)历届真题解析》 🌸 专栏介绍:中国电子学会《全国青少年软件编程等级考试》Python编程(1~6级)历届真题解析。 🚀 订阅专栏:订阅后可…...
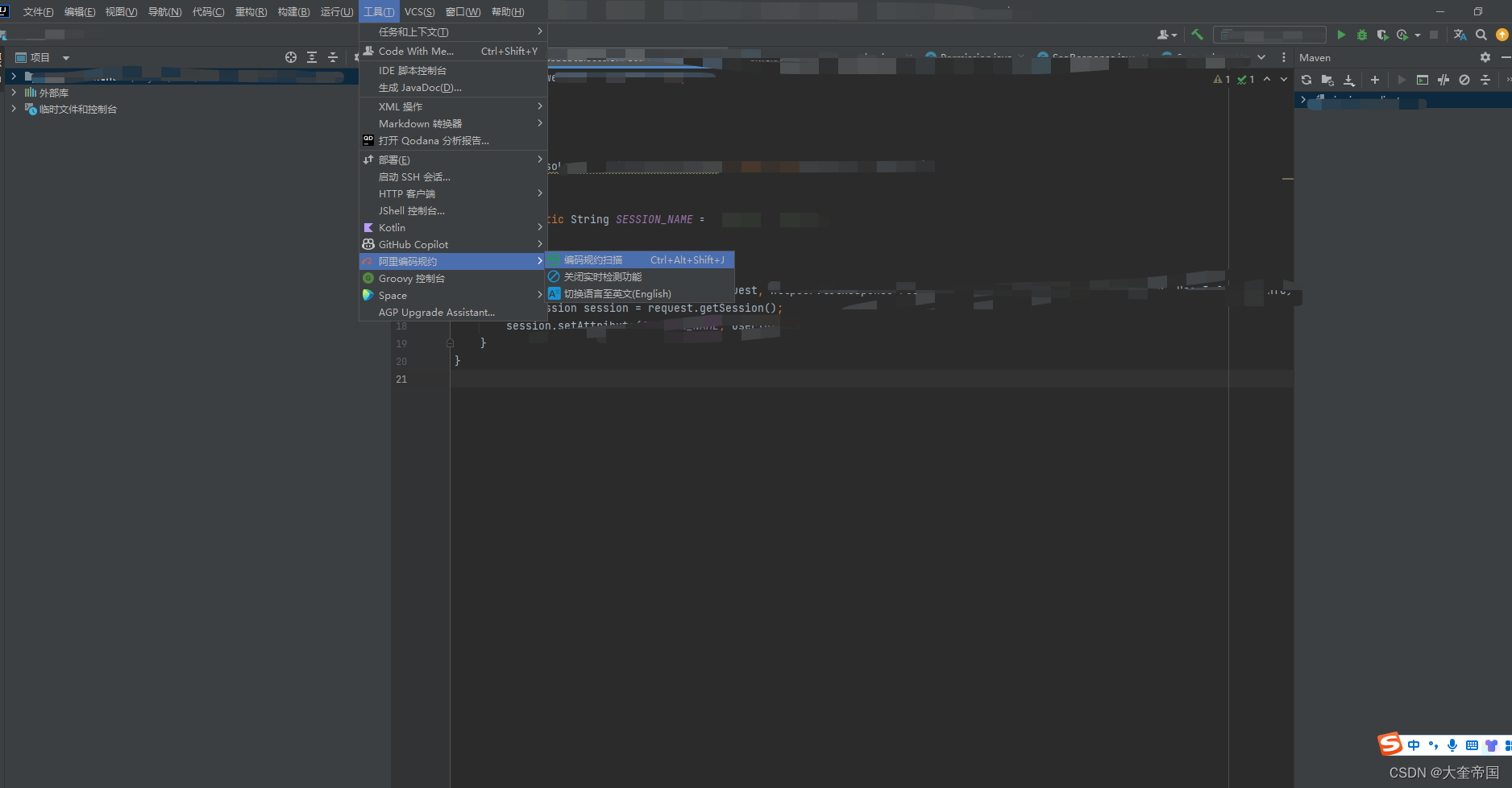
在IntelliJ IDEA 中安装阿里P3C以及使用指南
在IntelliJ IDEA 中安装阿里P3C以及使用指南 1.关于阿里p3c1.1说明1.2什么是P3C插件1.3p3c的作用是什么 2 如何在IDEA中安装p3c2.1 插件安装2.2 插件使用 3.参考连接 1.关于阿里p3c 1.1说明 代码规范检查插件P3C,是根据《阿里巴巴java开发手册(黄山版)》转化而成的…...
Java集成支付宝沙箱支付,详细教程(SpringBoot完整版)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、开发前准备?二、使用步骤1、引入库2、配置在 application.yml 里面进行配置:3、alipay的java配置:AplipayConfig.java4、支付…...
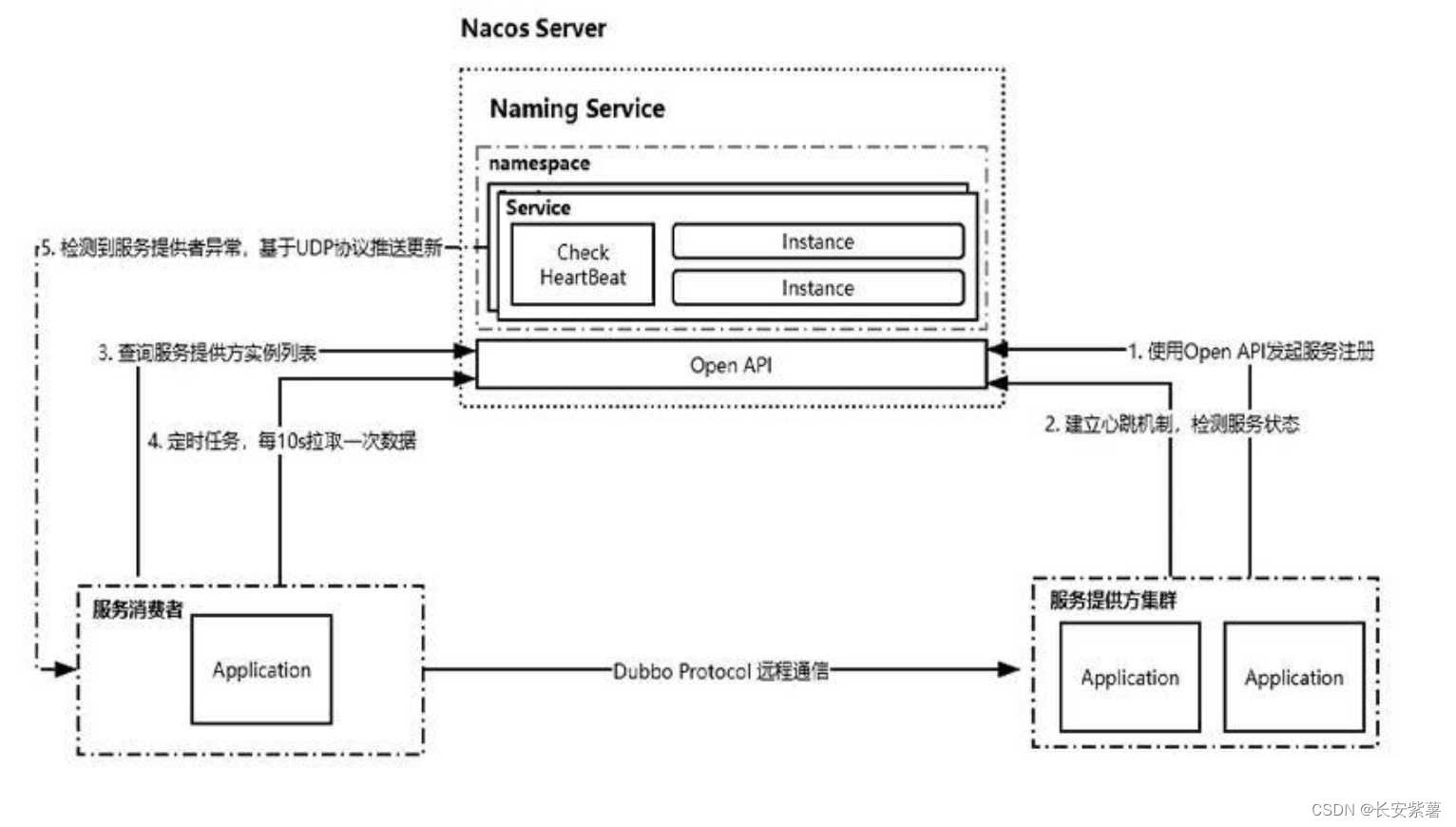
详解Nacos和Eureka的区别
文章目录 Eureka是什么Nacos是什么Nacos的实现原理 Nacos和Eureka的区别CAP理论连接方式服务异常剔除操作实例方式自我保护机制 Eureka是什么 Eureka 是Spring Cloud 微服务框架默认的也是推荐的服务注册中心, 由Netflix公司与2012将其开源出来,Eureka基于REST服务开发,主要用…...

在Vue中实现组件间的通信(父子通信,非父子通信,通用通信)
在vue中实现组件间的通信 文章目录 在vue中实现组件间的通信1、组件通信1.1、不同的组件关系和组件通信方案分类1.2、组件通信的解决方案1.3、非父子通信- event bus事件总线 2、prop2.1、prop详解2.2、prop校验2.3、prop & data、单向数据流 3、v-mdoel原理 1、组件通信 …...

LLaMA参数微调方法
1.Adapter Tuning:嵌入在transformer中 新增了一个名为adapter的结构,其核心思想是保持模型其他原始参数不变,只改变adapter的参数,其结构如下图所示: 1.在每一个transformer模块最后都加入一层adapter。 2.adapter首…...
NSSCTF之Misc篇刷题记录(17)
NSSCTF之Misc篇刷题记录(17) [闽盾杯 2021]DNS协议分析[GFCTF 2021]pikapikapika NSSCTF平台:https://www.nssctf.cn/ PS:所有FLAG改为NSSCTF [闽盾杯 2021]DNS协议分析 数据包提示给得是DNS数据包 直接过滤一下 发现 数据里面存…...
(算法图论基础入门))
红与黑(bfs + dfs 解法)(算法图论基础入门)
红与黑问题 文章目录 红与黑问题前言问题描述bfs 解法dfs 解法 前言 献给阿尔吉侬的花束( 入门级bfs查找 模版解读 错误示范 在之前的博客当中,详细地介绍了这类题目的解法,今天为大家带来一道类似的题目练练手,后续还会更新更有挑战的题目…...

为何学linux及用处
目前企业使用的操作系统无非就是国产类的,windows和linux类。我们要提升自己的技能,需要学习这两款。我记得在大学时期,学习过windows以及linux,但当时觉得又不常用,就学的模棱两可。毕业之后,你会发现&…...

ChatGPT高级数据分析功能
目录 只需上传数据集,系统即可自动进行分析。我们首先进行了一次测试。准备了一份关于二手车的数据,其格式如下: 接下来调用,GPT中的高级数据分析功能,上传数据,并要求进行分析 第一步:自动对数据字段进行详细的解释: 第二步,对数据进行预处理,比如缺失值,基本的…...

共享WiFi贴项目怎么实施与运营,微火为你提供高效解答!
共享WiFi贴是一项有前景的商业项目,不仅可以满足用户对网络的需求,还可以为创业者带来盈利的机会。那么,我们来看看如何有效地开展共享WiFi贴项目。 最重要的是选择合适的位置。共享WiFi贴项目的成功与否很大程度上取决于位置选择。优先选择人…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
